尝试与猜测———《鸡兔同笼》教学思考与实践

甘卫星

【课前思考】

一、教材本质——“假设、验证法”

教材是先呈现“鸡兔同笼”的历史原题，再将原题改成数据较小的例题，最后引导学生填表解决问题。通过自主探究、合作交流，让学生经历列表举例方法，引领学生经历从假设验证到有序列表再到一次调整的过程，明确数量关系。特级教师牛献礼在《沟通联系 突出思想——“鸡兔同笼”教学实践与思考》一文中写道：沟通多种方法之间的内在联系，揭示其本质上都是“假设—比较—调整”的思维方式。

二、设计本质——“假设、调整法”

学生对此题数学本质的理解几乎是零起点，不同尝试方法本质上是一致的，每一种方法都是“假设—比较—调换”这样一种循环往复的思维过程，是假设法的不同表现形式。因此，本节课的设计以沟通逐一尝试、跳跃尝试、一次尝试等不同的列举方法之间的内在联系，渗透假设思想的本质，聚焦尝试假设法。

【教学过程】

一、揭题引入，明确基本信息

师：同学们请看屏幕，今天我们来研究鸡兔同笼问题，知道鸡兔同笼的意思吗？

师：鸡兔同笼是一种数学问题，早在1500年前我国数学著作《孙子算经》中记载这样的趣题：鸡兔同笼，有9 个头，26 条腿。鸡兔各有几只？

（板书：鸡头+兔头=9 鸡腿+兔腿=26）

师：你读懂哪些信息？猜一猜这个笼子里可能有几只鸡？有几只兔？

预设：2 只鸡，7 只兔。

师：谁有不同的意见？

师：在碰到新问题时可以用猜测的方法来尝试解决问题。

（板书：尝试 猜测）

师：学习有趣的推理一课时我们用什么方法进行有序记录？

生：表格式。

【设计意图：通过谈话，理清已知信息以及隐藏信息之间的基本数量关系，为后续的假设、尝试、验证奠定基础。】

二、初识“假设—比较—调整”，理解“鸡兔互换”的规律

1.出示问题：鸡兔同笼，有9个头，26 条腿。鸡兔各有几只？

2.借助表格整理解题过程。

（1）学生独立完成。

（2）学生上台填写发现的内容。

3.反馈学生作业。

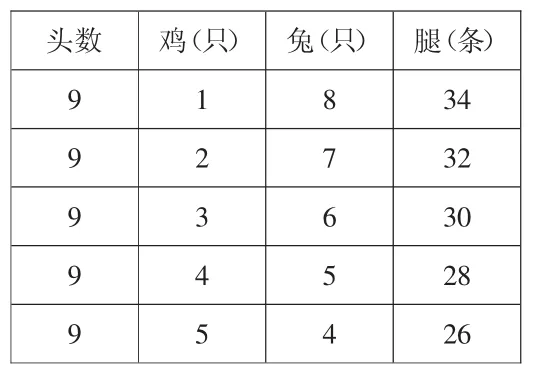
头数 鸡（只） 兔（只） 腿（条）9 1 8 34 9 2 7 32 9 3 6 30 9 4 5 28 9 5 4 26

4.对比发现规律。

师：腿的条数是怎样变化的？谁的只数变化会使腿数减少？

小结板书：鸡增加1 只，兔减少1 只，腿数就会减少2 条。

师：通过刚才的学习，你对尝试有什么认识？

师：刚才我们用列表举例的方法来解决鸡兔同笼的问题，发现了鸡兔同笼问题的规律，只要按照这样的方法和步骤，不管头数和腿数是多少都能找到答案吗？

【设计意图：此环节的设计，尊重学生已有的知识经验，既有独立思考，又有合作交流，充分发挥学生的自主能动性。例题从简单入手，化难为易，发现规律。在解决问题的过程中发现表格的用处，在表格中发现规律。让学生感悟到1 只鸡与1 只兔进行交换，脚的总数量会相差2，并直观理解“相差2”是怎么发生的。通过与实际脚数比较，逐步调整，直至调整到正确答案。这整个过程，便是“假设—比较—调整”的循环往复的过程。】

三、运用“假设—比较—调整”，加深对尝试法的理解

1．出示历史名题：《孙子算经》中有这样一道趣题：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？

师：我们能用刚才的方法解决这道题吗？

2．学生独立完成，小组交流。

3.反馈学生的方法，明确调整的方向。

（1）逐一尝试。

头数 鸡（只） 兔（只） 腿（条）35 34 1 72 35 33 2 74…… …… …… ……35 24 11 92 35 23 12 94

师：从1 鸡34 兔（或1 兔34鸡）开始，逐一检验排除，“地毯式搜索”直至找到正确结果为止。

（2）跳跃的尝试（出示两张）。

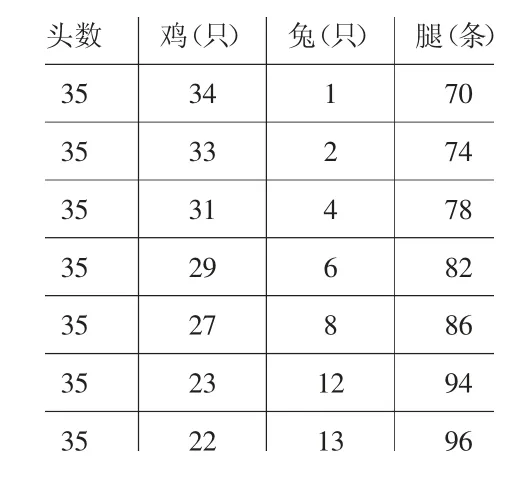
头数 鸡（只） 兔（只） 腿（条）35 34 1 70 35 33 2 74 35 31 4 78 35 29 6 82 35 27 8 86 35 23 12 94 35 22 13 96

头数 鸡（只） 兔（只） 腿（条）35 1 34 138 35 5 30 130 35 10 25 120 35 15 20 110 35 23 12 94 35 25 12 90

（学生解释自己的尝试过程）

师：从1 鸡34 兔（或1 兔34鸡）开始，跳过几个尝试；或直接折半（从17 鸡18 兔）开始试；或者经过几轮尝试直接跳到正确的结果。

（比较两张表格，重点说明第一次假设好后，通过比较，该往哪个方向调整）

（3）一次的尝试。

（学生解释自己尝试的过程）

师：腿多了2 只，应该如何调整？

生：将1 只兔换成1 只鸡，腿就少2 条，一共多了44 条腿，那就要交换22 只。

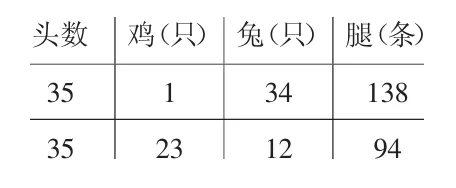
头数 鸡（只） 兔（只） 腿（条）35 1 34 138 35 23 12 94

生：将1 只兔换成1 只鸡，腿就少2 条，一共多了4 条腿，那就要交换2 只。

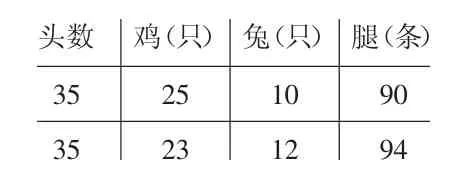
头数 鸡（只） 兔（只） 腿（条）35 25 10 90 35 23 12 94

生：将1 只鸡换成1 只兔，腿就多2 条，一共少了8 条腿，那就要交换4 只。

头数 鸡（只） 兔（只） 腿（条）35 27 8 86 35 23 12 94

【设计意图：在这个环节，比较各种列表解决数学问题的方法，分析异同，找出优势，帮助学生找到解决鸡兔同笼问题的基本方法。重点放在假设好以后再进行比较、再如何调整的教学上，从任意假设，一只一只进行调整，到后来跳跃式调整，再到后面一次性调整到位，从思维低层次水平逐步到高层次水平，循序渐进，逐步理解如何假设、如何调整。通过列表“假设—比较—调整”，让学生经历假设的全过程，发现这种规律为进一步抽象成算式表征提供感性的经验。】

四、多层次练习，巩固尝试法

1．快速反应。

（1）一个笼子里有鸡和兔共35 只，它们的脚一共有130 只，鸡和兔各有几只？

（2）一个笼子里有鸡和兔共35 只，它们的脚一共有80 只，鸡和兔各有几只？

2．过关练习。

有龟和鹤共40 只，龟的腿和鹤的腿共有112 条。龟和鹤各有多少只？

（1）理解题意。

（2）请学生独立解决。

（3）重点说清怎么想的，说清楚假设的整个过程。

（4）介绍：日本的“龟鹤算”问题就是从我国的“鸡兔同笼”问题演变来的。

3．拓展提升。

师：我们一直都在研究笼里的鸡和兔，它们可被我们逼急了，去了趟花果山，学会了十二般变化，藏在下面三个场景中，你们还能找到它们吗？

春游：要参加春游，妈妈给了我20 张人民币，告诉我一共是175元，其中只有5 元和10 元的两种，你知道5 元和10 元各多少张吗？

投篮：一名篮球运动员在一场比赛中一共投中9 个球，有2分球，也有3 分球，这名运动员一共得了21 分，他投中2 分球和3分球各多少个？

下棋：学校有象棋、跳棋，共26 副，恰好供120 个学生同时活动，象棋2 人下一副，跳棋6 人一副，那么象棋和跳棋各几副？

4.小结。

师：这里的鸡不仅仅是鸡，兔也不仅仅是兔，“鸡兔同笼”只是这类问题的一个统称。生活中有许多类似“鸡兔同笼”的问题，也能用今天学习的方法去解决。

【设计意图：通过三个层次的练习，旨在巩固学生对本课核心方法“假设—比较—调整”的理解和掌握。巩固解决鸡兔同笼问题的解题方法——列表法，培养学生运用所学知识解决实际问题的能力。让学生明白解决的方法都是假设法，并提炼出简单的问题模型。把模型演绎到各种生活现象和问题情境中，促进模型的进一步内化。】