原子辅助光力系统中快慢光的量子调控*
谷开慧 严冬 张孟龙 殷景志 付长宝
1) (吉林大学电子科学与工程学院, 长春 130012)
2) (长春理工大学光电信息学院光电科学分院, 长春 130114)
3) (长春大学理学院, 材料设计与量子模拟实验室, 长春 130022)
4) (通化师范学院物理学院, 通化 134000)
随着纳米科技以及半导体技术的迅猛发展, 光力诱导透明、快慢光和光存储以及其他在光力系统中发现的量子光学和非线性光学效应成为人们目前研究的热点. 本文将薄膜腔光力系统同被束缚在腔中的二能级冷原子系综相耦合, 通过直接在薄膜振子上引入弱辅助驱动场来研究该原子辅助光力系统中原子和相位对量子相干性质及其快慢光的调控. 经过分析发现, 通过改变辅助驱动场的强度可直接实现对光力诱导透明窗口深度的调控, 通过改变辅助场与探测场之间的相位差, 可实现输出的探测场在“吸收”、“透明”和“增益”之间相互转换, 进而对弱探测场进行动态调控实现光开关. 与此同时, 还发现系统的群延迟时间随相位差的改变呈周期性变化. 通过调节相位差及原子数, 不但可以改变群延迟时间, 还可实现快慢光之间的相互转换.
1 引 言
随着纳米技术和半导体工艺的迅猛发展, 人们越来越关注光力学这个新领域, 它为人们在高精密测量、量子信息处理以及量子基本原理的验证等方面打开了一扇大门. 近年来, 光力系统实现了一些经典的量子光学现象, 例如Agarwal和Huang[1]在Fabry-Perot (FP) 腔光力系统中发现了类似原子的电磁诱导透明现象(electromagnetically induced transparency, EIT), 即光力诱导透明现象(optomechanically induced transparency, OMIT),同原子中的电磁诱导透明一样, 光力诱导透明效应不仅促进了量子光学的发展, 同时也在快慢光[2-7]、光存储[8-11]和光开关[12,13]等量子信息处理方面有着广泛的应用. 此外, 在光力系统中人们还实现了机械振子的基态冷却[14,15], 在宏观物体上观察到相干态[16]、压缩态[17,18]和纠缠态[19-23]等量子现象. 然而, 目前大部分典型腔光力学系统仍然只涉及两个自由度之间的耦合, 超过两个自由度耦合的多元光力学系统较少受到研究者关注.
最近在杂化的、多模的光力学系统中发现了一些奇异的量子现象, 例如量子态转移[24]、声子诱导透明[25]、相干完美吸收及相干完美透射[13,26,27]等,这些研究成果在量子信息处理方面有着潜在的应用价值, 因此成为当前光力学的一个研究趋势. 同时在原子辅助光力系统中, Chang等[28]、Fu等[29]和韩明等[30]发现了电磁诱导透明的多稳现象,Yan等[31]则在与FP腔耦合的具有偶极-偶极相互作用的里德伯超级原子系综中发现了双稳现象, 另外还观察到了EPR (Einstein-Podolsky-Rosen)态的产生[32]以及基态冷却[33-35]等量子现象. 但是在原子辅助光力系统中通过相位调控快慢光的研究则较少见. 很明显这种杂化光力学系统中, 原子-腔-薄膜振子三模耦合, 原子作为辅助物质扮演着一个非常重要的角色, 它同光力系统的相互作用通过腔模联系起来, 控制原子可改变光力学腔中的腔场, 进而影响整个杂化光力系统的量子相干性, 从而实现对快慢光的量子调控, 因此原子辅助光力系统比常见的光力系统表现出了更多的量子操控自由度.
本文研究在弱辅助驱动场直接激发薄膜振子的原子辅助光力系统中, 原子和相位对OMIT及快慢光的调控. 首先讨论如何通过改变辅助场与探测场的相位差及振幅比来实现对OMIT的控制,同时实现输出的探测光在“吸收”、“透明”和“增益”之间相互转换, 进而对弱探测光进行动态调控实现光开关. 其次讨论如何通过调节相位差及原子数来改变群延迟时间, 使其表现出慢光或快光效应以及快慢光之间的转换. 本文的研究有助于该系统应用于存储光脉冲、全关开关、光电倍增管等量子光机械器件的研制工作.
2 物理模型与计算
考虑如图1所示的原子辅助光力系统, 它由线性耦合的薄膜腔光力系统和被束缚在其中频率为的个全同二能级87Rb超冷原子系综构成, 其中二能级的量子?态⟩ 和?分别⟩ 对应87Rb原子的线的量子态和. 选择的薄膜振子的本征频率为, 弛豫速率为, 其力学品质因子为. 如图1, 整个系统由外加的一个频率为的强驱动场和一个频率为的弱探测场驱动, 而薄膜振子则是直接由弱辅助驱动场驱动, 这三个外加相干场之间的频率假设满足
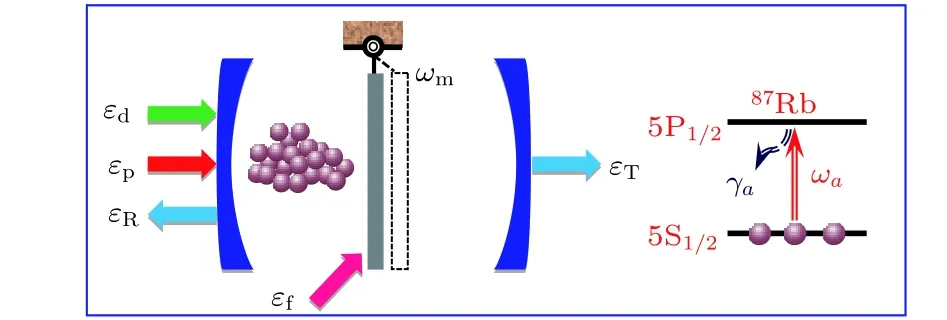
图1 由单模FP腔以及束缚在其中的N个全同二能级87Rb冷原子系综和中间由弱辅助驱动场 驱动的振动频率为 的薄膜振子构成的光力学系统, 该系统的探测场和驱动场分别为 和Fig. 1. Schematic diagram of an optomechanical cavity containing N identical two-level cold 87Rb atoms with two fixed-end mirrors of equal reflectivity, which is driven by a strong coupling field , a weak auxiliary drive field and probed by a weak field .
这里只考虑单模腔场的情况, 则系统总的哈密顿量为

式中右侧三项依次分别代表腔场的能量、原子的能量和薄膜振子的能量. 其中为单模腔场的本征频率,和分别表示腔中光子的湮灭和产生算符,它们之间满足对易关系.表示原子在能级和之间的跃迁√ 频率, 在弱激发及原子数条 件 下 ,表 示 集 体 跃迁算符[28,29], 满足对易关系. 由于中间的薄膜振子在其平衡位置做微小振动, 所以可用量子谐振子模型来描述其量子性质, 写成声子产生算符()和湮灭算符 ()的形式, 满足对易关系. 第二项为原子-腔和腔-薄膜振子相互作用哈密顿量
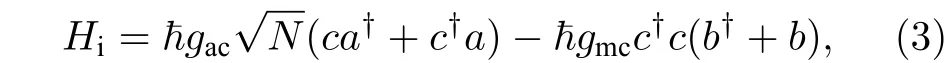
式中右侧两项分别代表腔场同原子系综之间的相互作用和腔√场与薄膜机械振子之间的相互作用. 其中表示腔场与原子之间相互作用的耦合系数,表示原子跃迁的电偶极矩,表示腔的体积,表示真空介电常数. 光力耦合系数用表示. (1) 式中的第三项为三个外加输入场与腔场和薄膜振子相互作用哈密顿量
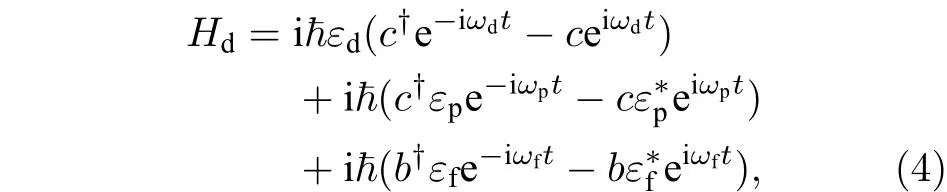
式中右侧三项分别代表腔外输入的强驱动场和弱探测场与腔场之间的相互作用以及弱√辅助驱动场与薄膜振子之间的相互作用. 其中,驱动场、探测场和辅助驱动场的输入振幅,,和分别代表驱动场、探测场和辅助驱动场的输入功率.
在得出系统总的哈密顿量之后, 通过海森伯-郎之万方程研究体系的动力学性质,
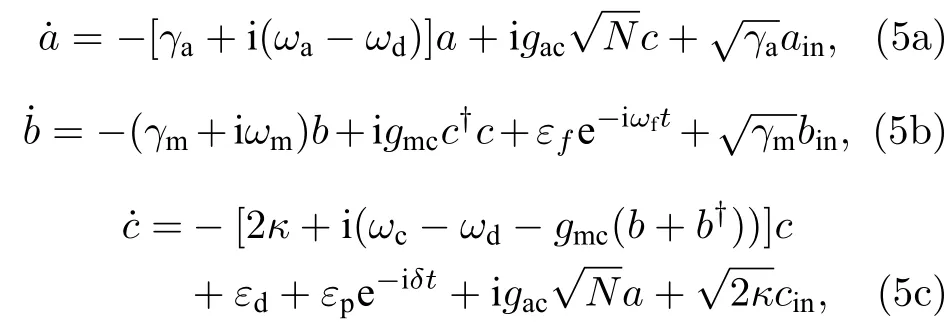

稳态平均值:
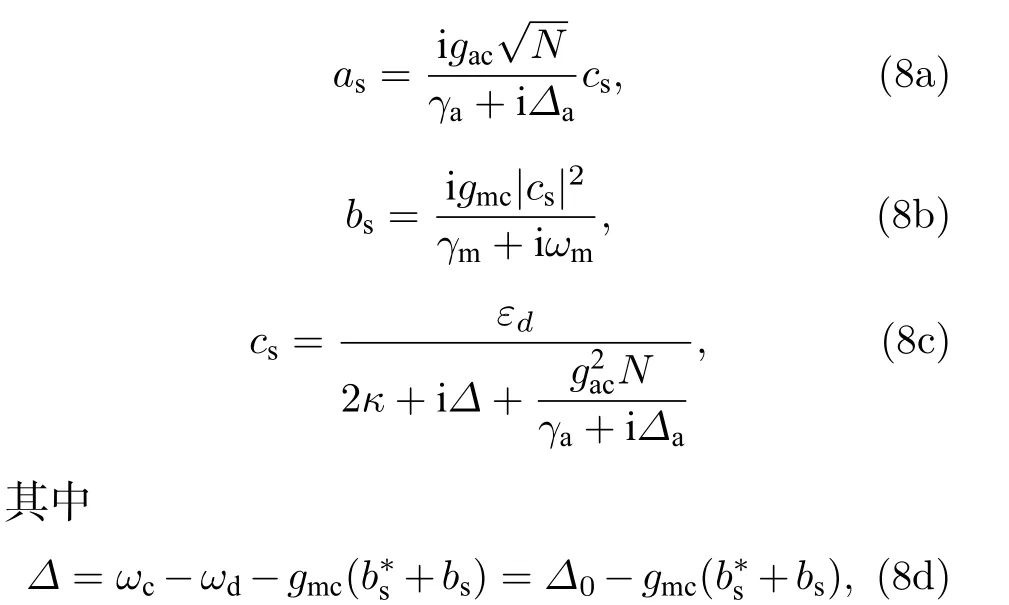
表示腔场的有效失谐, 包含光压效应.
本文主要研究该原子辅助光力系统对探测场的线性响应, 所以在情况下,把系统算符写成各自平均值及其微小涨落的和:

将(9)式代入(7)式中, 并且只保留线性项,忽略非线性项,,和平均值为零的量子热噪声项, 可得涨落算符平均值满足的方程为:


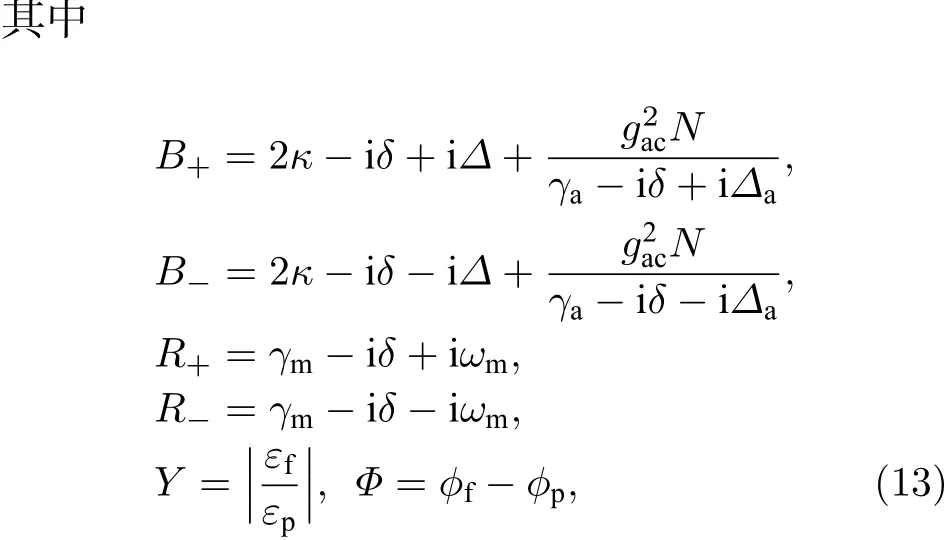
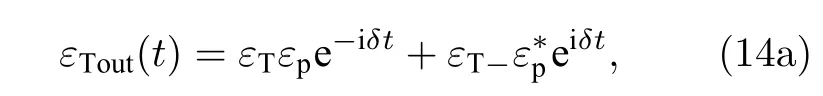
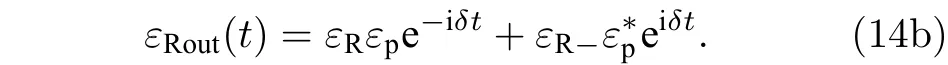
由腔的输入输出关系[36]
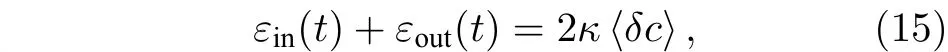
得到
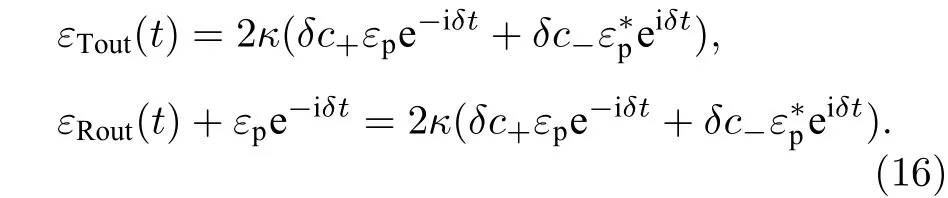
由此可得
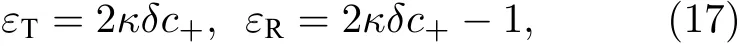
相应地, 根据(17)式可得到群延迟时间[7]为:
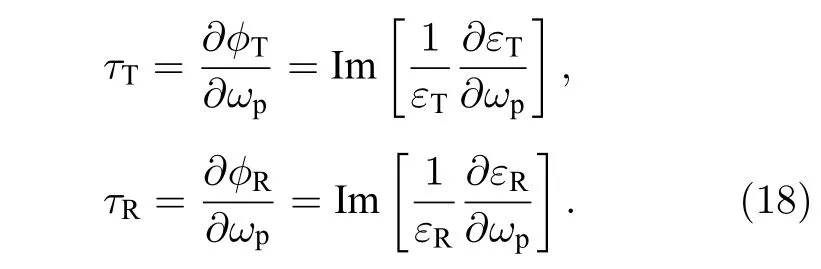
群延迟时间如果大于零, 则系统表现出慢光现象,群延迟时间如果小于零, 则为快光现象.
3 讨 论
以下主要讨论原子辅助光力学腔中相位对OMIT及快慢光现象的影响. 本文采用的是实验上真实可行的实验参数[29,33], 并满足劳斯-胡尔维茨稳态判定准则[36], 确保系统稳态的稳定性. 各参数具体值为:mm,ng,MHz,MHz.
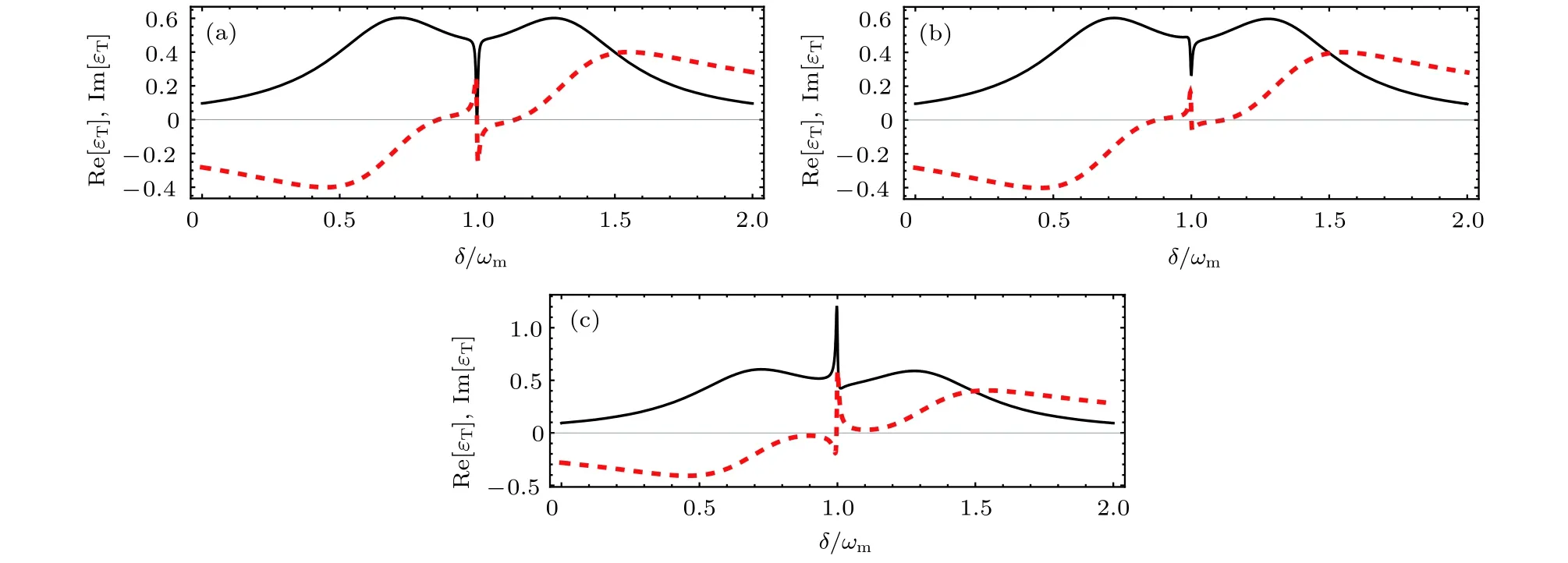
图 2 (黑 色 实 线 )和 (红 色 虚 线 )随 频 率 失 谐 的 变 化 曲 线 (a) ; ; (b) ; ;(c) ; ; 其他参数值见文中第 4 部分Fig. 2. The real (black line) and the imaginary (red dotted line) parts of as a function of with (a) ; ;(b) ; ; (c) ; . Relevant parameters are the same as those in Sec. 4.
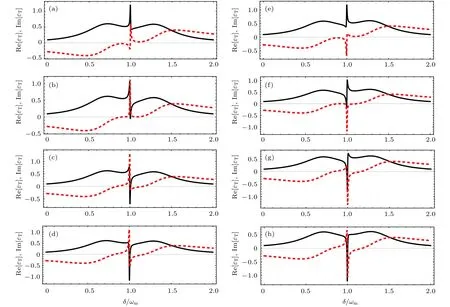
图3 时 (黑色实线)和 (红色虚线)随频率失谐 的变化曲线 (a) ; (b) ; (c) ;(d) ; (e) ; (f) ; (g) ; (h) ; 其他参数值见文中第 4 部分Fig. 3. The real (black line) and the imaginary (red dotted line) parts of as a function of with : (a) ;(b) ; (c) ; (d) ; (e) ; (f) ; (g) ; (h) . Other parameters are the same as those in Sec. 4.
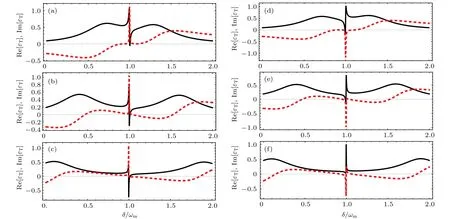
图 4 时 (黑 色 实 线 ) 和 (红 色 虚 线 ) 随 频 率 失 谐 的 变 化 曲 线 √ MHz; (e) , MHz; 其他参数值见文中第 4 部分Fig. 4. The real (black line) and the imaginary (red dotted line) parts of √as a function of√ MHz; (d) MHz; (e) MHz. Other parameters are the same as those in Sec. 4.
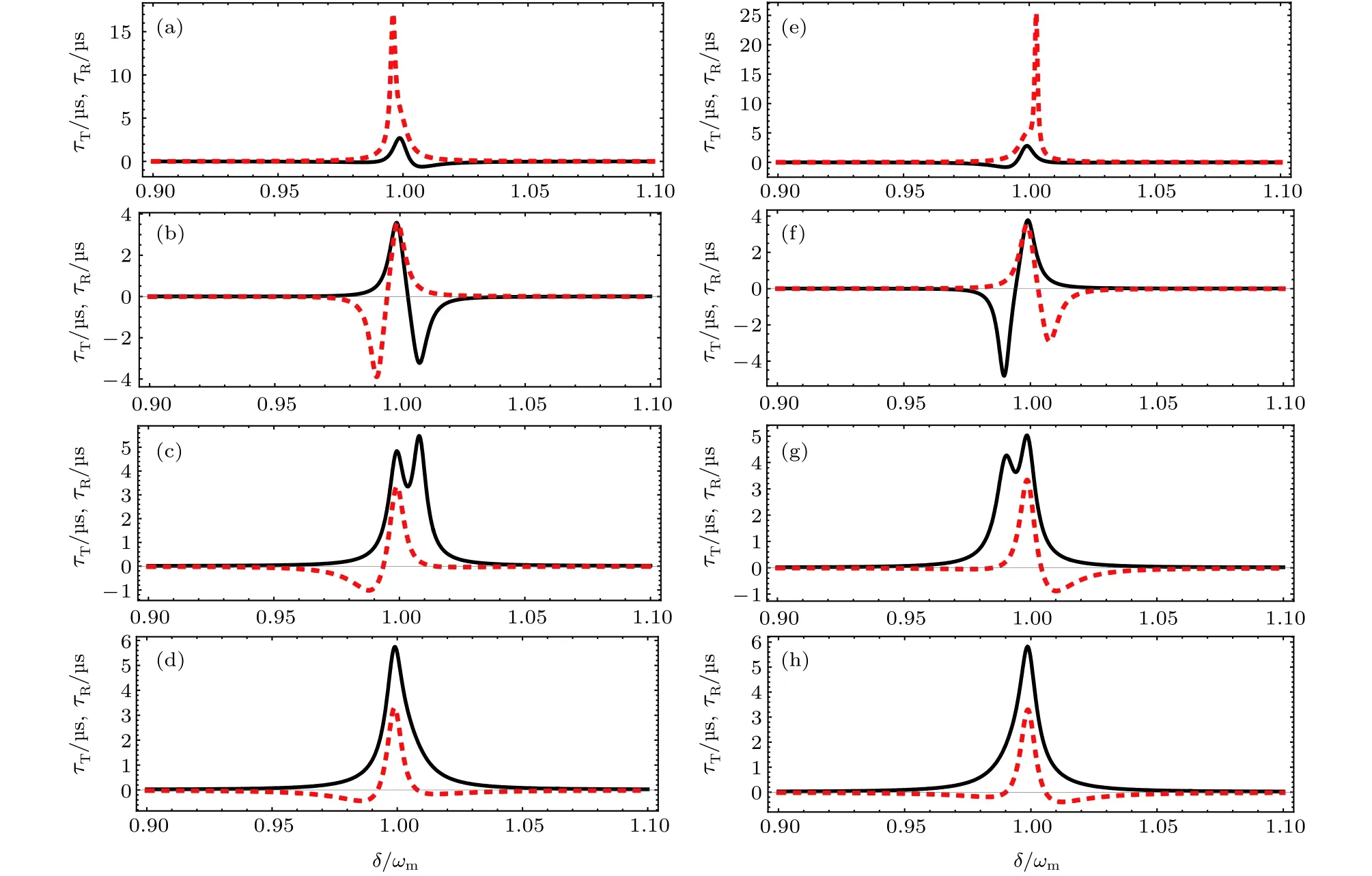
图5 (黑色实线)和 (红 色虚线)随频率失谐 的变 化曲线: (a) ; (b) ; (c) ; (d) ;(e) ; (f) ; (g) ; (h) ; 其他参数取值同图 3Fig. 5. The (black line) and the (red dotted line) as a function of with (a) ; (b) ; (c) ;(d) ; (e) ; (f) ; (g) ; (h) . Other parameters are the same as those in Fig.3.
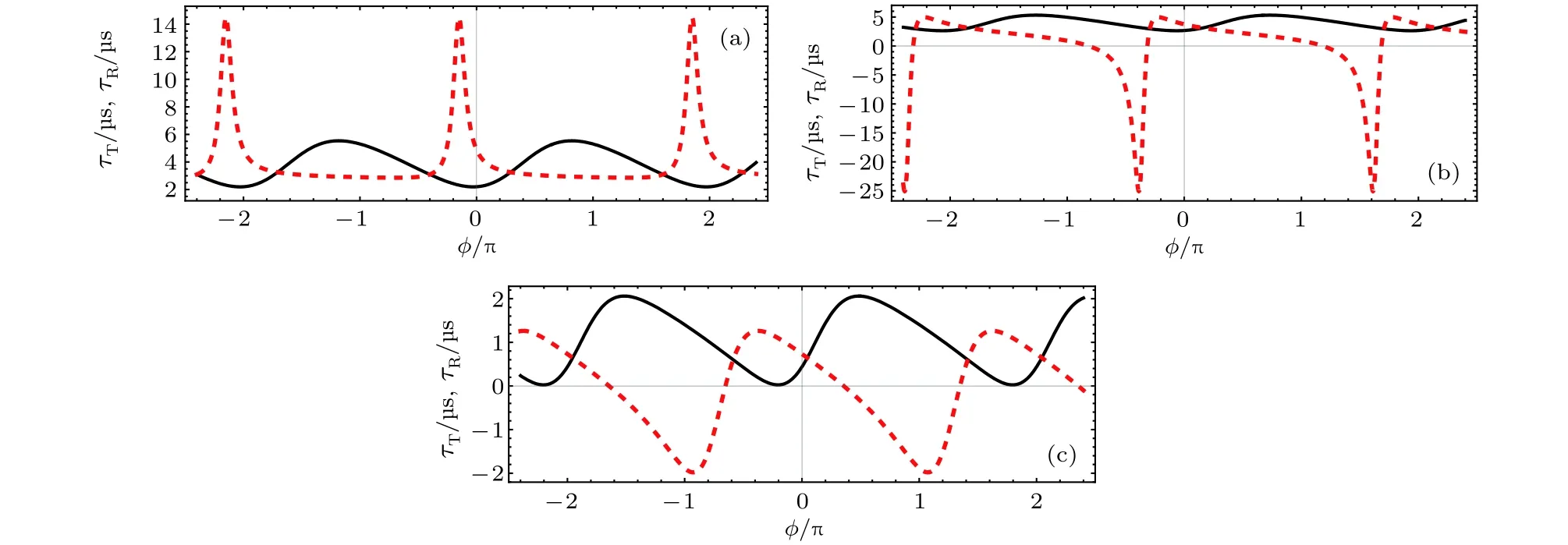
图 6 √时 (黑 色 实 线 )和 (红 色 虚 线 )√随 相 位 差 和 振 幅 比 的 变 化 曲 线 : (a) , MHz;(b) , MHz; (c) , MHz; 其他参数取值见文中第 4 部分Fig. 6. The (√black line) and the (red dotted lin√e) as a function of and Y with: (a), MHz;(b) , MHz; (c) , MHz. Other parameters are the same as those in Sec. IV.
4 结 论
本文主要研究了在薄膜振子上耦合弱辅助场的原子辅助光力系统中相位对OMIT及快慢光的调控. 当没有辅助场与薄膜振子耦合时, 在原子-腔-薄膜振子三模耦合的光力系统中观察到了杂化EIT和OMIT. 当辅助场直接激发薄膜振子且与探测场同相位时发现, 在共振处辅助场使薄膜振子产生共振吸收, 从而抑制了OMIT. 所以本文通过改变辅助场同探测场的相对振幅比, 直接影响了腔场与薄膜振子的光力耦合效果, 从而实现了对OMIT窗口深度的调控. 当保持辅助场与探测场振幅比不变, 只改变它们之间的相位差时发现, 相位差的取值也直接影响着系统的光力耦合效应, 使得仅通过调节相位就可以实现输出的探测场在“吸收”、“透明”和“增益”之间相互转换, 从而改变整个系统的吸收和色散性质. 与此同时, 发现群延迟时间随相位差的改变呈周期性变化. 通过调节相位差及原子数, 可以改变群延迟时间, 使其表现出慢光或快光效应以及快慢光之间的转换. 利用该系统不但可以通过相位的调节来操控光在“吸收”和“透明”之间相互转换从而实现全光开关, 同时还可以通过光在“吸收”、“透明”和“增益”之间相互转换实现光电倍增, 因而该系统在量子光学器件方面有着潜在的应用价值.

