基于新修正偶应力理论的Reddy型层合板的热稳定性分析

张大千，王良秀

(沈阳航空航天大学 航空宇航学院，沈阳 110136)

当材料的尺寸进入微米以及纳米量级时，已有实验表明材料的刚度、强度会明显增强[1-3]，这种现象被称为材料的尺度效应。研究表明经典连续体力学理论无法解释这一现象，为了研究这一现象，学者们提出了广义连续介质理论，如应变梯度理论、偶应力理论等。广义连续介质理论通过引入材料尺度参数来解释材料的尺度效应，不同的理论引入的材料尺度参数不同。1963年Mindlin[4]提出了经典偶应力理论，理论中应变对称曲率张量不对称，转角与位移不独立，且含有一个材料尺度参数。2002年Yang等[5]人提出了修正偶应力理论，进一步将曲率张量对称化。基于此理论，Ma[6]等人建立了非经典Mindlin层合板模型；Park等[7]建立了Bernoulli-Euler梁模型；Tsiatas[8]建立了Kirchhoff板模型。

以上研究中涉及的均是各向同性材料，并未讨论各向异性材料。2011年Chen[9]等人首次提出适用于各向异性材料的新修正偶应力理论，理论中应变张量与偶应力力矩张量对称，曲率张量不对称。在此基础上，Li、Ma[10-11]建立了Timoshenko层合梁的自由振动模型以及Reddy型层合板模型；Chen等[12]建立了Reddy型层合板的整体-局部理论；Mohammadabadi[13-14]等进行了复合材料层合微梁热屈曲及振动尺寸效应分析；Chen等[15]对Mindlin层合板进行了屈曲分析以及有限元分析；Chen[16]对Reddy型层合板进行了稳定性分析；Wanli.Yang[17]等研究了Mindlin层合板在斜交铺设时不同几何形状和边界条件下，铺设角对尺度效应的影响。

以上学者的研究中均未涉及微尺度下各向异性Reddy层合板的热稳定性研究，基于此，本文以新修正偶应力理论为基础，建立了微尺度下Reddy板热稳定性模型，模型中只引入一个材料尺度参数，当尺度参数为零时可以退化为经典理论模型。用该模型对微尺度下Mindlin板进行了热稳定性分析。

1 新修正偶应力理论

2011年Chen[9]等人重新书写了修正偶应力理论中部分本构方程，将偶应力力矩张量对称化，理论中应变张量与曲率张量表达如下

(1)

式(1)中ωi,j=∂ωi/∂j(i=x，y=j),应力张量σ和对称化得到的偶应力力矩张量m本构关系如下

(2)

式(2)中λ、G为Lame系数，i、j为材料尺度参数，表示的是微观尺度下材料的缺陷或夹杂的尺度的度量，若将理论应用于各向同性材料，则模型自动退化为各向同性修正偶应力。

2 新修正偶应力理论Reddy层合板热稳定性模型

2.1 新修正偶应力Reddy层合板位移场及应变与曲率

在整体坐标系下，用u,v,w表示层合板上任意一点x、y和z方向位移，ωx、ωy和ωz分别代表转动位移，如图1所示。

图1 层合板示意图

Reddy层合板位移场如下：

u(x,y,z)=u0(x,y)+zθy(x,y)-cz3(θy+w,x)

v(x,y,z)=v0(x,y)-zθx(x,y)-cz3(-θx+w,y)

w(x,y,z)=w0(x,y,z)

(3)

式(3)中u0、v0、w为层合板中面沿直角坐标系x，y，z个方向的位移，θx，θy分别为横法线绕y轴和x轴的转角。c=4μ/3h2，μ为模型控制参数，当μ=1时为Reddy板；当μ=0时为Mindlin板；当μ=0且θx=∂w/∂x且θy=-∂w/∂x时为Kirchhoff板。转动位移为定义为ω=1/2curlu，将式(3)带入转动位移表达式中得到转动位移如下

(4)

当温度改变量为ΔT时，Reddy型层合板的应变与曲率张量可表示为

(5)

式中αx,αy分别为层合板沿x,y轴方向的热膨胀系数。将式(3)和式(4)带入式(5)可得层合板的应变和曲率如下

(6)

(7)

2.2 单层层合板本构方程

在局部坐标系下，第k层层合板的本构关系如下

σ′k=Ckε′k

(8)

式(12)中

(9)

Qk=TkTCkTk

(10)

第k层层合板在整体坐标系下热膨胀系数为

(11)

式(11)中m=cosφk，n=sinφk，φk为第k层沿x方向铺设角。第k层层合板在整体坐标系下的本构关系为

σk=Qkεk

(12)

(13)

对于单层层合板而言是正交各向异性的，因此其刚度矩阵如下

(14)

式中

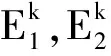
Qk=

式(15)中

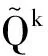
2.3 新修正偶应Reddy层合板的虚功原理及热稳定性模型

基于新修正偶应力理论的Reddy层合板的虚功原理可表示为

δU-δW=0

(16)

δU为内力虚功，δW为外力虚功，表达式如下

(17)

将式(13)带入式(17)可进一步得到内力虚功表达式

(18)

式(18)中

Nx,Ny,Nxy,Nx1,Nx3,Ny1,Ny3,Nxy1,Nxy3,Qxz,Qyz,Qxz2,Qyz2,Yx,Yy,Yxy,Yyx,Yx2,Yy2,Yxy2,Yyx2

表达式为

(19)

(20)

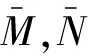
(21)

将式(6)、式(7)、式(12)及式(19)带入式(21)可得到具体控制方程如下

A1u0,xx+A2u0,yy+A3v0,xy+A4w,xxx+A5w,xyy+

A6θx,xy+A7θy,xx+A8θy,yy+fu=0

B1u0,xy+B2v0,xx+B3v0,yy+B4w,yyy+B5w,xxy+

B6θx,xx+B7θx,yy+B8θy,xy+fv=0

C1u0,xxx+C2u0,xyy+C3v0,yyy+C4v0,xxy+C5w,xx+

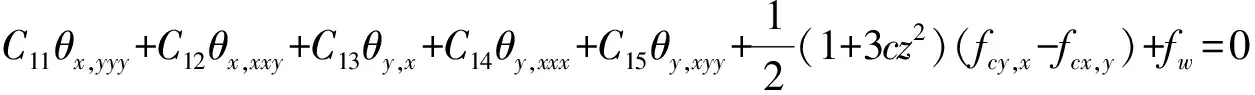
E1u0,xy+E2v0,xx+E3v0,yy+E4w,y+E5w,yyy+

E6w,xxy+E7θx,xx+E8θx,yy+E9θy,xy+E10θx-

(22)

四边简支层合板边界条件为

(23)

仅考虑板受热载荷作用，相对于板的横向位移w，膜向位移u0，v0是小量，方程中忽略uo，v0且假设fu=fv=fcx=fcy=0，化简方程(22)得到正交Reddy层合板仅考虑热载作用下的控制方程为

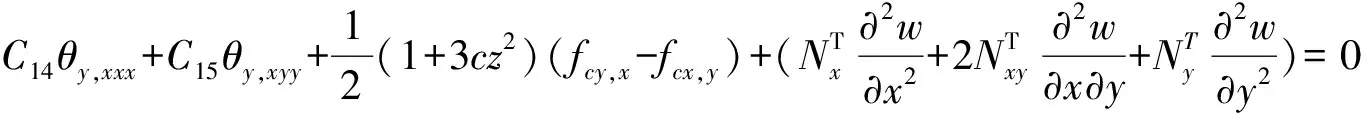
D4w,x+D5w,xxx+D6w,xyy+D7θx,xy+D8θy,xx+D9θy,yy+D10θy=0

E4w,y+E5w,yyy+E6w,xxy+E7θx,xx+E8θx,yy+E9θy,xy+E10θx=0

(24)

其中

(25)

满足全部边界条件的位移函数为

(26)

α=aπ/L，β=bπ/L，将式(26)带入式(24)可得到

(27)

临界屈曲温度ΔT可由式(27)可求得。同理，若考虑轴向载荷作用时，正交Reddy层合板在热载荷和轴向载荷共同作用下的稳定方程为

(28)

其中

由此可求得受轴向压缩时正交Reddy层合板在温度改变量为ΔT时的失稳临界载荷，当=0时退化为经典正交Reddy层合板稳定理论，当=0且θx=∂ωy/∂x，θy=∂ωx/∂y可退化到经典Kirchhoff板稳定理论。

3 数值算例

3.1 计算临界温度

计算仅考虑在热载荷作用下四边简支方板铺设角为[90，0，90]和[0，90，0]时的临界温度随材料尺度参数(10-6)的变化，计算结果如表1、表2所示。其中板厚h=2×10-5m，L=10h，材料常数[18]：E2=6.98×109Pa，E1=25E2，G12=0.5E2，G22=0.2E2，ν12=ν22=0.25。当铺设角为[90,0,90,0]时，材料常数相同与热膨胀系数与文献[18]相同，为α1=10×10(-6)/℃，α2=25×10(-6)/℃。将应用本模型求出的临界温度转换成热载荷，视其为作用在层合板的双向等压载荷，其大小与文献[16]计算得到的层合板受双向等压时的屈曲载荷吻合良好，验证了本模型的正确性。从表1表2可以看出：a=1,b=1(a、b为位移模数[19]，a=1、2、3、4，b=1、2)时临界温度最小；新修正偶应力理论下的临界温度均大于经典理论下的临界温度，验证了尺度效应的存在。a、b相同时不同铺设角下临界温度不同，说明铺设角对尺度效应有一定影响。随着材料尺度参数的增加，临界温度增加，尺度效应增强；随着a，b的增加，临界温度也在增加。

表1 铺设角为[90，0，90]四边简支方板在热载荷作用下临界温度随材料尺度参数的变化

3.2 板的跨厚比对临界温度以及尺度效应的影响

取h=2×10-5m，材料常数与算例1相同，分别计算铺设角为[0，90，0]和铺设角为[90，0，90]时不同材料尺度参数下临界温度随跨厚比与材料尺度参数(10-6)的变化。图2表明，随着跨厚比的增加临界温度的值在减小，尺度效应也在减弱，材料尺度参数越大，临界温度下幅度降越剧烈，尺度效应越明显。当跨厚比相同时，临界温度随着材料尺度参数的增加而增大且均大于经典理论临界温度，验证了材料尺度效应的存在。

表2 铺设角为[0，90，0]四边简支方板在热载荷作用下临界温度随材料尺度参数的变化

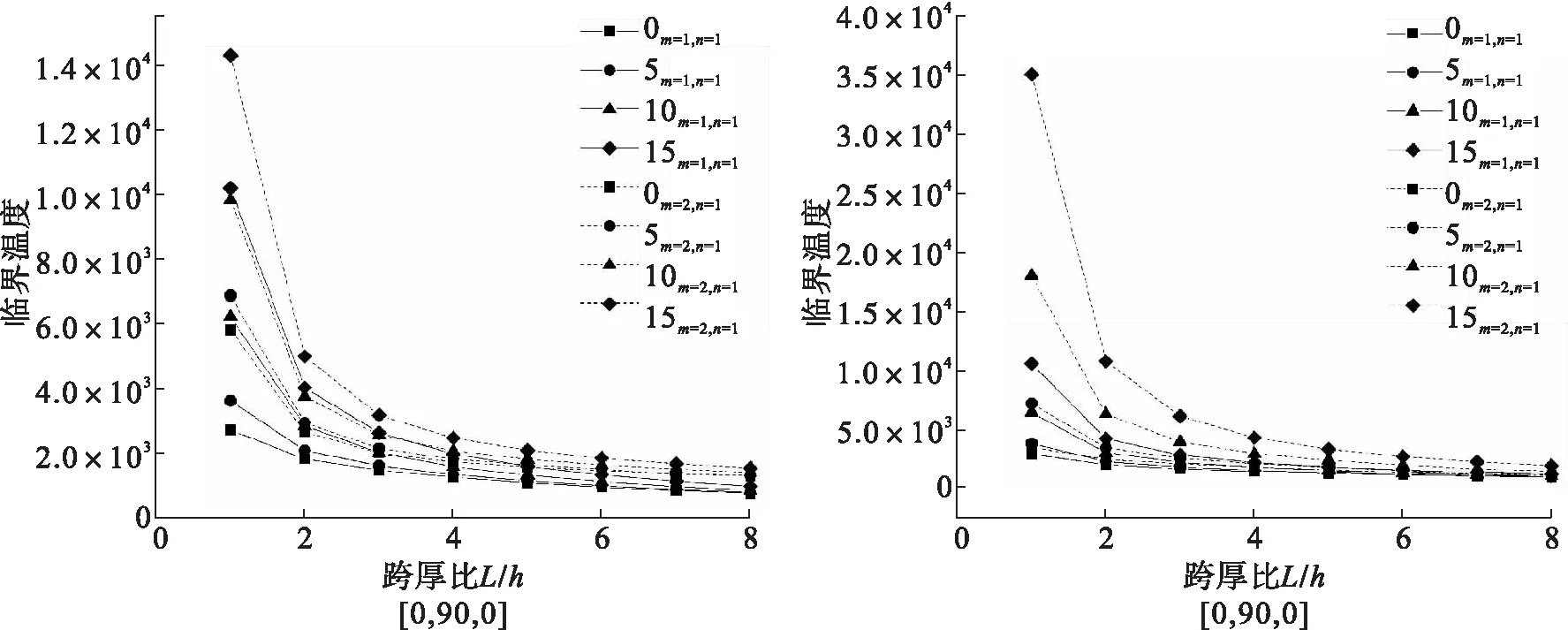
图2 临界温度随跨厚比L/h与材料尺度参数变化

图3 单向轴压四边简支方板临界载荷随温度与h/的变化

3.3 ΔT对尺度效应以及屈曲载荷的影响

取L=10h，材料的长度尺度参数取为：=6×10-6m，材料常数与算例1相同。对铺设角为[90，0，90]计算温度变化为ΔT时外载荷为单向轴压和铺设角为[0，90，0]温度变化为ΔT时外载荷为双向等压时基于新修正偶应力理论的临界载荷和经典理论下的临界载荷。

图4 双向等压四边简支方板临界载荷随温度与h/的变化

图3和图4中实线代表的是新修正偶应力理论失稳临界载荷，虚线代表的是经典理论下失稳临界载荷。计算结果表明：新修正偶应力理论下的失稳临界载荷总是大于经典理论下的失稳临界载荷。随着温度ΔT的升高，两者差距加大，h/越小，两者差距越明显，尺度效应越明显；尺度参数越大，尺寸效应也越明显，表明在有温度变化时不能忽略温度载荷对失稳临界载荷的影响。

4 结论

本文基于新修正偶应力理论推导出了考虑热载荷作用下Reddy层合板的控制方程以及边界条件。当材料尺度参数为零时，该模型自动退化为经典理论模型，尺度效应会随着板几何参数的加大而逐渐消失退化为宏观理论。当a,b增加时临界温度也在增加，利用该模型求出了临界温度、不同跨厚比下的临界温度以及考虑热载荷作用下的屈曲载荷。主要结果如下：

(1)当a=1,b=1时基于本模型算出的临界温度总是大于经典理论下的临界温度，捕捉到了尺度效应；不同铺设角对尺度效应有影响；材料尺度参数越大，临界温度越高，尺度效应越明显。

(2)随着板的跨厚比的增加临界温度在减小，跨厚比越小，尺度效应越明显。

(3)随着ΔT的增加，考虑热载荷作用下的屈曲载荷与经典理论下的屈曲载荷差距加大，尺寸效应也随之加大且当h/越小，尺度效应越明。