“对称法”在解决高中物理碰撞问题中的应用

马云荣

一、由一道碰撞习题掀起对碰撞的研究

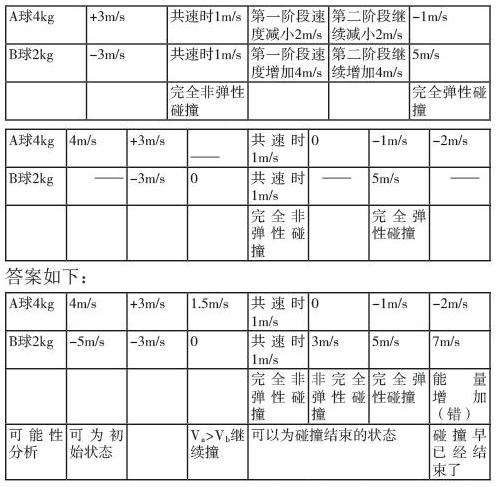
碰撞的结果不可能出现在初始速度的前面，也不可能出现在共速之前，因为主动球还有撞击的能量。碰撞的结果只能出现在共速之后的一个范围内，就看势能是否能完全转化回动能。也不可能出现在完全弹性碰撞的速度之后，因为没有势能提供更多的动能。拓展一下我们的思维：所有的碰撞问题都可以用这些简单的数字游戏来计算了。我们可以称之为“对称法”，什么对称呢？在完全弹性碰撞中，产生形变过程与恢复形变过程对称;力的大小时刻对称;我们把两个碰撞物体的始末情况都摸清了，就不用担心能量会增加，不用担心碰撞后前者速度小于后者速度等等，这些问题统统都在计算的表格中展示清楚了，根本不会出现这种可能。简而言之，碰撞的结果谁说了也不算。不是题目给一组数据我就被动地去计算，它本来有它该有的样子，我找到它该有的样子就完全可以应对任何问题。

二、用“对称法”巧妙得出完全弹性碰撞的速度公式

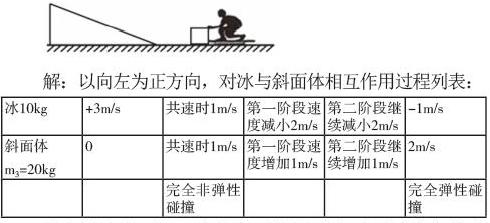
由表格计算可知：冰从斜面体滑到水平面时速度是向右的1m/s，而小孩与冰分离后速度是向右的1m/s，速度相等，一定追不上。这种“对称法”的应用使得学生对过程理解更加清晰，也必须建立在对物理规律的理解之上。本题第一件事是以小孩和冰为系统，解决小孩的后撤速度;第二件事是冰与斜面体相互作用的动量与能量变化问题，包括对称的两个过程，可以把初速度、共速度、末速度一一破解出来，对问题的理解大有好处，同时也避免了特别繁琐的二元一次方程组计算。但要特别注意，对规律的应用万万不可以淡化，一定要求學生会用规律列方程。

在高中阶段，理解物理概念和物理规律是重中之重，是不断培养学生物理素养和提高物理能力的手段。但是，一旦把学生限于繁琐的数学计算中，而又总是得不到正确的答案，我就会考虑是否老师给的方法太古板，太不实用，是否有更加实惠的好办法呢！期待这样的办法越来越多，把物理的学习变得不枯燥，变得有意思起来！