长大货物多式联运路径再利用规划模型与算法

雷定猷，曾斌祥，王哲

长大货物多式联运路径再利用规划模型与算法

雷定猷1, 2，曾斌祥1, 2，王哲1, 3

(1. 中南大学 交通运输工程学院，湖南 长沙 410075；2. 轨道交通安全教育部重点实验室，湖南 长沙 410075；3. 智慧交通湖南省重点实验室，湖南 长沙 410075)

通过将单个节点拆分为不同运输方式的同位节点，货物换装视为虚拟运输边，构建长大货物多式联运网络，适当保留改造后的节点与边，建立联运通道以提高长大货物运输经济效益。考虑公、铁、水路运输、经济等各类影响因素，建立以收益投资比值BCR最大化为优化目标的长大货物多式联运路径再利用规划模型。提出基于固定优先权编码的遗传算法，以选择最佳运输路径、换装方式以及网络改进措施。研究结果表明：多式联运在运输费用以及运输时间方面优势明显；采用再利用规划后的路径运输长大货物对比公、铁联运路径运输长大货物，其运输费用和时间分别降低10.6%和26.0%，收益投资比可达1.261 6。

交通规划；路径再利用规划；多式联运；遗传算法；运输网络设计问题；运输通道

公路大件货物、铁路超限超重货物、水路重大件货物统称为长大货物[1]。因长大货物具有超长、超宽、超高和超重等固有属性，其多式联运路径往往需要进行一定程度改造，以满足长大货物运输要求。现有长大货物运输过程中，受政策、经济等因素影响，大量长大货物运输采用路径临时改造方案，无法重复利用。从现代物流或经济学角度分析，路径临时改造方案存在优化空间，且不利于国家可持续发展战略的实施。因此，本文针对现有长大货物运输存在的不足并结合长大货物多式联运客观需要，提出长大货物多式联运路径再利用规划问题，即在已有长大货物多式联运路网中添加节点与边或对已有节点与边进行改造(为叙述方便，下文统称为改造)，从而构建长大货物运输通道，以改善网络运输能力。长大货物多式联运路径再利用规划问题属于具体化的运输网络设计问题TNDP[2-6]。因此，遗传算法等通用启发式算法被用于解决运输网络设计问题[7-9]。Bazaras等[10]探讨了基于既有公路运输网络的长大货物运输路径选择标准。程博等[11]提出了改进遗传模拟退火算法用于对公路运输大件货物路径的优化选择。Lukić等[12]研究了铁路阔大货物在塞尔维亚和欧洲南部之间运输组织问题。Yamada等[13]建立了一个货物多式联运的双层规划模型，以收益投资比值最大化为目标，对已有货物运输网络进行改造。Petraška等[14]设计了一套专门用于长大笨重货物运输的评估标准，并研制了一个路径选择系统。郑燕等[15]以运输费用、时间以及碳排放量为优化目标，研究了长江流域汽车整车公水联运路径的选择。既有研究主要侧重于单一运输方式的路径规划，极少针对长大货物多式联运路径进行再利用规划，且一般优化目标为费用最小或收益最大，缺乏收益投资比的考量。鉴于既有文献对长大货物多式联运路径再利用规划问题研究的不足，本文建立以收益投资比BCR最大化为优化目标的长大货物多式联运路径再利用规划模型，并提出一种基于固定优先权编码的遗传算法用于求解。验算结果表明，该算法可以从联运网络和改进措施中选择最佳运输路径、换装方式以及网络改进措施。

1 长大货物联运网络拓扑与模型

1.1 长大货物多式联运网络拓扑

图1为长大货物多式联运网络拓扑，包含公铁水路3层运输网络。实线代表真实运输边，不同颜色虚线为虚拟运输边，代表货物换装。位于同一垂直线的节点称为同位节点，即地理位置相同运输方式不同。如图1(a)中节点4，5和6互为同位节点。根据实际情况，部分节点无同位节点或只有一个同位节点。3个同位节点之间最多允许2次换装，2个同位节点最多允许换装一次。图1(b)为图1(a)的扩展长大货物多式联运网络拓扑，即其中单个节点或边改造费用不超出许可费用，则假设对所有可以实施改造措施的节点和边进行改造，从而得到改造后的网络拓扑。

1.2 路径再利用规划模型

(a) 初始网络拓扑；(b) 扩展网络拓扑

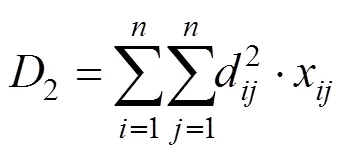
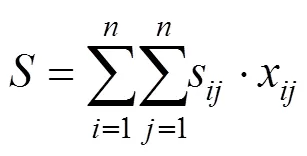
式(8)中为构建通道后的收益，包括线路使用费用、节点吊机使用费用等纯收益，不包含未来长大货物运输所节约的临时改造费用、纯运输费用，以及运输里程、运输时间量化后的费用。其中为收益年期，为年序号，a为边(,)未来第年的预期收益，为居民消费价格指数。

式(11)和(12)保证改造前后将货物从节点v到节点v运输时间(包括改造时间)不超过允许时间。

这便是运用计算思维解决问题的一般方式，在学习和生活中，遇到任何问题，首先应该去思考如何运用此种方式方法来进行问题的分析、思考、解决等。久而久之，便能逐渐提高系统、科学的思维能力和思考习惯。

式(13)保证改造后的运输与改造费用之和不超过允许费用。

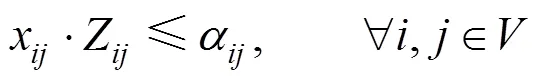
式(15)保证轴载不超过公路、铁路以及桥梁安全承载能力，其中车辆装载货物后轴载Z，公路、铁路以及桥梁允许轴载α。

式(16)保证节点装卸能力，其中长大货物质量为，节点v起重重量为。

2 基于固定优先权编码的遗传算法

由于本文问题解的特殊性，0-1和整数等编码方式都不能很好地表达该问题的解。程博等[11]提出基于优先权编码方法，即对路径的导向性信息进行编码。然而，直接利用上述算法进行编码仍然会出现非法解。经过对该问题的深入研究，利用本文提出的固定优先权编码方式对路径进行编码，可以很好地表达该问题的解，以实现对运输路径、货物换装以及网络改进措施的优化选择，且在进行遗传操作时不会产生非法解。

2.1 基于固定优先权编码的染色体

2.1.1 固定优先权编码

固定联运网络中特殊节点(仅有一条边与其相连，起始、终止节点除外)的优先权值，使其优先权值小于上一节点的相邻节点的优先权值以保证路径的延伸。此外，固定起始节点优先权值最小，终止节点优先权值最大，以保证路径顺利从起点延伸至终点。除特殊节点和起始节点，运输网络中其余节点取随机优先权值。表1为图1(a)联运节点的优先权值，其服从固定优先权编码思想。图1(a)中节点11为特殊节点，即固定此类特殊节点优先权值小于上一节点的相邻节点优先权值，禁止节点11成为节点6的下一节点。

表1 联运节点优先权

2.1.2 解码

根据表1信息，从节点1出发，节点2和3与其相连，因节点2优先权大，所以节点2为下一节点。以此类推，从起始节点1到终止节点15的完整路径为1→2→5→6→9→7→10→12→15。若同位节点之间存在换装两次的情况，则选择下一延伸节点时忽略同位节点，防止路径延伸陷入循环换装。

2.2 遗传算子

2.2.1 交叉

为解决交叉操作产生非法子代的问题，GEN 等[16]提出权重映射交叉。该编码方式常应用于与本文染色体结构类似的2阶段以及固定费用运输问题[17]。然而，直接利用权重映射交叉法对本文染色体进行交叉，同样存在产生非法子代的问题。因此，本文提出固定权重映射交叉法，基本原则是在采用权重映射交叉法的基础上，变更交叉后染色体中特殊节点的优先权值，使其小于上一节点的相邻节点的优先权值，且保证调整后的节点优先权值大小相对顺序不变。具体操作步骤如下。

步骤1：随机选择交叉点。 交叉点↓

联运节点123456789101112131415 优先权值父代1161134912728101314515 父代2136913118541071421215

步骤2：交换父代基因串。

联运节点123456789101112131415 优先权值父代1161134912721071421215 父代2136913118548101314515

步骤3：对交换部分基因串，按照优先权值从小到大进行排序，生成映射关系。该映射关系可以理解为交叉部分节点权值的排列顺序。

步骤4：按映射关系再次交换基因串，产生中间子代。

联运节点123456789101112131415 优先权值子代1161134912721081451315 子代2136913118547101214215

步骤5：调整子代特殊节点(假设节点11和14为特殊节点，其上一节点的相邻节点分别为4，5，9及13，15)优先权值，使其优先权值小于上一节点的相邻节点的优先权值，产生最终子代。需要注意的是，在调整优先权值时，需要保持相邻节点权值大小顺序不变。例如调整之前权值大小排序为节点5>节点4>节点9，调整后权值大小排序不变。

联运节点123456789101112131415 优先权值子代1161148912731021413515 子代2136101311859741214215

2.2.2 变异

随机选择父代中2个基因，交换基因值。检查节点权值，若特殊节点优先权值不满足编码规则，则按照交叉算子步骤5的规则，变更特殊节点的权值。该方法能最大限度地减小变异对整个染色体的影响，从而更好地实现局部爬山，搜索到更好的解。

2.2.3 解有效性检验

步骤1：按解码规则生成联运路径。

步骤2：计算各联运路径运输费用、时间，改造费用、时间等各项结果。

步骤3：检验联运计算结果是否满足模型约束条件。不满足则剔除种群中相应个体。按照该编码方式生成新的个体，再次检验。直至所有个体生成的路径均满足模型约束。

2.2.4 进化选择

本文采用轮盘赌模型进行子代的选择。选择的过程就是旋转轮盘若干次，每次为新种群选出一个个体，个体适应值越高则个体被选中的几率就 越大。

3 算例分析

某企业承运一台HD变压器，其质量约为250 t，尺寸为10 850 mm×3 460 mm×4 850 mm。运输期限为60 d，运输、改造资金分别为600万和1 000万。直接计算a较为困难，因此通过调研以及结合地理位置、现有长大货物运量、国家政策、相关文献数据等因素对通道收益进行估算，其通道收益约为投资的0.9~1.2倍。时间与里程转换系数和分别取值0.5万元/d，0.01万元/km，居民消费价格指数为2%。运输、换装费用以及时间参考表2承运长大货物公司计算公式。

表2 计算公式

3.1 长大货物运输方案-未实施改造措施

货主要求将货物从秦皇岛市(节点1)运送至普洱换流站(节点30)。根据模型约束条件对节点与边进行筛选后，初始长大货物多式联运网络如图2(a)所示。图2(a)对应信息见表3。

(a) 初始联运网络；(b) 扩展联运网络

遗传算法参数设置：初始种群个体数量为20，最大遗传代数为200代，交叉、变异概率分别为0.8和0.01。经过计算，若采用纯公路运输，其运输路径为1→4→6→9→13→16→21→30，广义运输费用(包括纯运输费用以及运输时间与里程量化后的费用)456.65万元，运输时间80.7 d，运输里程3 863 km。若采用多式联运，最优运输路径为1→4→5→7→10→14→13→16→21→30，包括公、铁路运输。其中广义运输费用388.727 5万元，运输时间44.4 d，运输里程3 988 km。由以上结果可知，多式联运相比纯公路运输，其在运输费用以及运输时间方面优势明显。

3.2 长大货物运输方案−实施改造措施

货主要求将货物从秦皇岛市(节点1)运送至普洱换流站(节点32)。图2(b)为基于图2(a)的扩展运输网络，其对应信息见表4，改造信息见表5。

表3 联运网络信息

表4 扩展联运网络信息

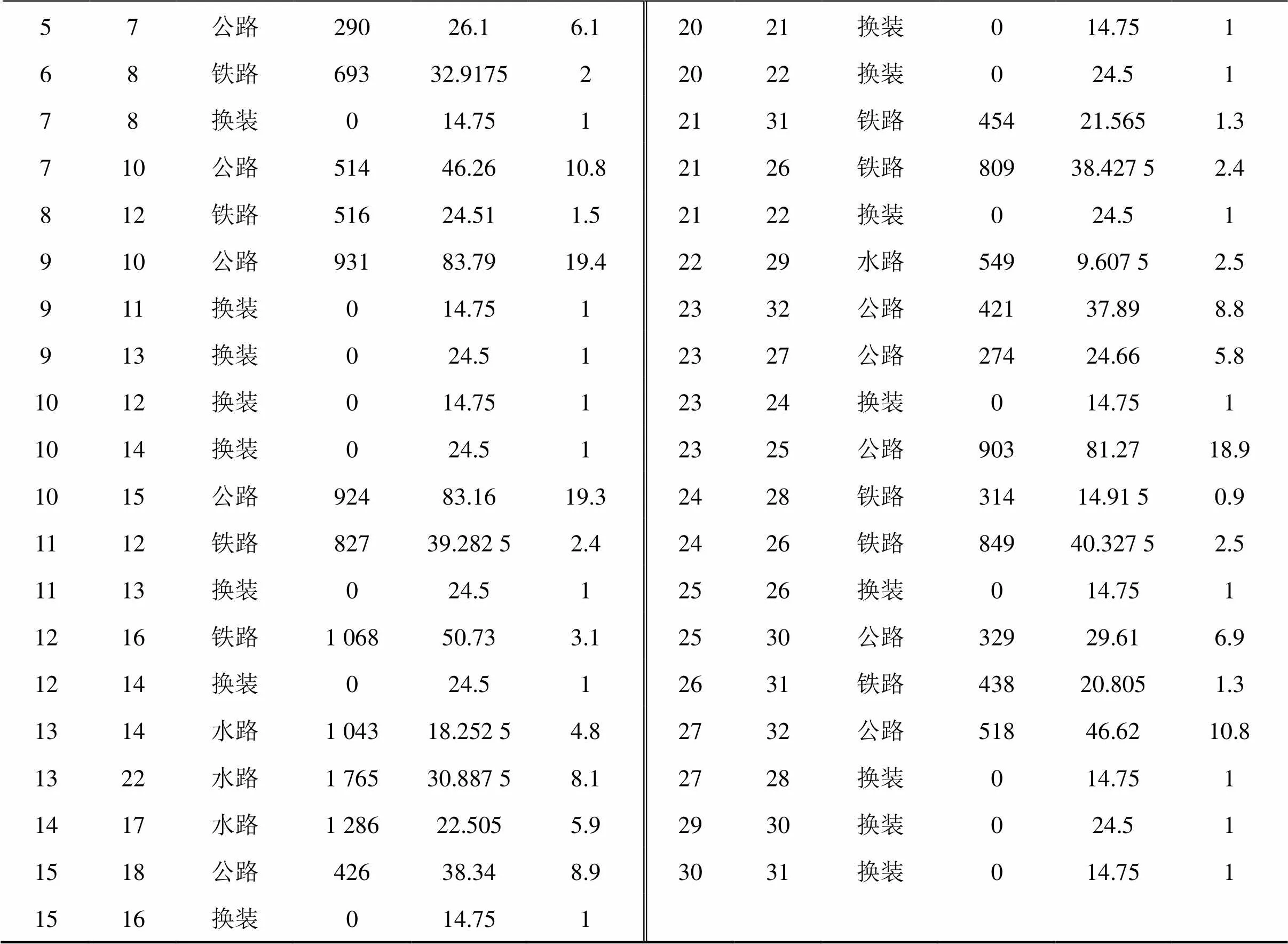
57公路29026.16.12021换装014.751 68铁路69332.917522022换装024.51 78换装014.7512131铁路45421.5651.3 710公路51446.2610.82126铁路80938.427 52.4 812铁路51624.511.52122换装024.51 910公路93183.7919.42229水路5499.607 52.5 911换装014.7512332公路42137.898.8 913换装024.512327公路27424.665.8 1012换装014.7512324换装014.751 1014换装024.512325公路90381.2718.9 1015公路92483.1619.32428铁路31414.91 50.9 1112铁路82739.282 52.42426铁路84940.327 52.5 1113换装024.512526换装014.751 1216铁路1 06850.733.12530公路32929.616.9 1214换装024.512631铁路43820.8051.3 1314水路1 04318.252 54.82732公路51846.6210.8 1322水路1 76530.887 58.12728换装014.751 1417水路1 28622.5055.92930换装024.51 1518公路42638.348.93031换装014.751 1516换装014.751

表5 网络改造信息

经过计算，在实施改造措施之后广义运输费用347.325万元，运输时间32.84 d，运输里程5 241 km。运输路径为1→3→4→13→22→29→30→31→26→ 24→23→32，包括公、铁、水路运输。需要对节点29和节点30进行改造，改造时间7 d，改造费用600万元。

图3(a)，3(b)和3(c)为各子项对比图。由图3可知，采用改造后路径运输长大货物，其运输费用相比公路、公铁联运分别减少109.325万元和41.4025万元，降幅分别达23.94%和10.65%；运输时间分别减少47.86 d和11.56 d，降幅分别达59.31%和26.04%。图3(d)为改造前后均采用最优路径运输长大货物的BCR比值迭代图。在迭代约100次，种群收敛得到最大BCR。即通过构建运输通道，最终收益投资比BCR达1.261 6。因此，通过算例结果可知，数学模型可以完整地概括路径再利用规划问题。利用所提算法求解可知采用再利用规划路径进行长大货物运输，在纯运输费用、时间方面收益提升明显，且可以通过构建通道进一步提高收益。

(a) 广义运输费用；(b) 运输时间；(c) 运输里程；(d) BCR迭代

4 结论

1) 针对现有长大货物多式联运的不足，提出长大货物多式联运路径再利用规划问题。统筹考虑各类影响因素，并以收益投资比值BCR最大化为优化目标，建立长大货物多式联运路径再利用规划 模型。

2) 设计一种基于固定优先权编码的遗传算法，实现了对运输路径、换装方式以及网络改进措施的优化选择。利用固定优先权编码以及固定优先权映射交叉法，解决了一般遗传算法编码和交叉过程中产生非法子代的难题，提升了算法性能。

3) 运用所提算法进行验算可知，在运输费用、时间方面多式联运方案优势明显。且通过合理改造，构建可重复利用的联运通道，运输时间、费用显著减少，其收益投资比可达1.261 6。为决策者提供了理论支撑以及具有实际操作意义的长大货物多式联运和路径改造方案。

[1] 雷定猷, 游伟, 张英贵, 等. 长大货物多式联运路径优化模型与算法[J]. 交通运输工程学报, 2014, 14(1): 75−83. LEI Dingyou, YOU Wei, ZHANG Yinggui, et al. Path optimization model and algorithm of multimodal transport for long and bulky cargo[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 75−83.

[2] GAO Z, WU J, SUN H. Solution algorithm for the bi-level discrete network design problem[J]. Transportation Research: Part B, 2005, 39(6): 479−495.

[3] Farahani R Z, Miandoabchi E, Szeto W Y, et al. A review of urban transportation network design problems[J]. European Journal of Operational Research, 2013, 229(2): 281−302.

[4] ZHANG L, YANG H, WU D, et al. Solving a discrete multimodal transportation network design problem[J]. Transportation Research: Part C, 2014, 49(49): 73−86.

[5] DI Z, YANG L, QI J, et al. Transportation network design for maximizing flow-based accessibility[J]. Transportation Research (Part B): Methodological, 2018(110): 209−238.

[6] AN K, HONG K L. Robust transit network design with stochastic demand considering development density[J]. Transportation Research: Part B, 2015(81): 737−754.

[7] ZHAO F, ZENG X. Simulated annealing–genetic algorithm for transit network optimization[J]. Journal of Computing in Civil Engineering, 2006, 20(1): 57−68.

[8] Nayeem M A, Rahman M K, Rahman M S. Transit network design by genetic algorithm with elitism[J]. Transportation Research: Part C, 2014(46): 30−45.

[9] Babazadeh A, Poorzahedy H, Nikoosokhan S. Application of particle swarm optimization to transportation network design problem[J]. Journal of King Saud University-Science, 2011, 23(3): 293−300.

[10] Bazaras D, Batarlienė N, Palšaitis R, et al. Optimal road route selection criteria system for oversize goods transportation[J]. Baltic Journal of Road & Bridge Engineering, 2013, 8(1): 19−24.

[11] 程博, 杨育, 刘爱军, 等. 基于遗传模拟退火算法的大件公路运输路径选择优化[J]. 计算机集成制造系统, 2013, 19(4): 879−887. CHENG Bo, YANG Yu, LIU Aijun, et al. Highway transportation route selection optimization based on improved genetic annealing algorithm[J]. Computer Integrated Manufacturing Systems, 2013, 19(4): 879− 887.

[12] Lukić L, Djapić M. Railway shipping of the largest energy transformer in the Balkan[J]. Mechanic Transport Communications, 2011(3): 7−12.

[13] Yamada T, Russ B F, Castro J, et al. Designing multimodal freight transport networks: A heuristic approach and applications[J]. Transportation Science, 2009, 43(2): 129−143.

[14] Petraška A, Palšaitis R. Evaluation criteria and a route selection system for transportating oversize and heavyweight cargoes[J]. Transport, 2012, 27(3): 327−334.

[15] 郑燕, 黄承锋, 张政. 长江流域汽车整车运输路径选择研究[J]. 公路交通科技, 2018, 35(6): 145−158. ZHENG Yan, HUANG Chengfeng, ZHANG Zheng. Study on path selection of finished automobile transport in Yangtze river valley[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 145−158.

[16] GEN M, Altiparmak F, LIN L. A genetic algorithm for two-stage transportation problem using priority-based encoding[J]. Or Spectrum, 2006, 28(3): 337−354.

[17] Lotfi M M, Tavakkoli-Moghaddam R. A genetic algorithm using priority-based encoding with new operators for fixed charge transportation problems[J]. Applied Soft Computing Journal, 2013, 13(5): 2711−2726.

Route reuse planning model and algorithm of multimodal transportation for long and bulky cargo

LEI Dingyou1, 2, ZENG Binxiang1, 2, WANG Zhe1, 3

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. Key Laboratory of Traffic Safety on Track, Ministry of Education, Changsha 410075, China; 3. Key Laboratory of Intelligence Traffic, Hunan Province, Changsha 410075, China)

Multimodal transportation network of long and bulky cargo was constructed by splitting single node into the same position nodes of different transportation modes and regarding the cargo transferring between different transportation modes as a virtual transportation edge. Reconstructed nodes and edges were appropriately reserved to construct a multimodal transportation corridor to improve the economic benefits of long and bulky cargo transportation. By considering various influencing factors such as road, railway, waterway transportation and economy, a multimodal transportation route reuse planning model based on maximizing the BCR (benefit/cost ratio) was established. Genetic algorithm based on fixed priority coding was proposed which can choose the best transportation route, transferring method and network improvement measures. The example results show that the multimodal transportation has obvious advantages in transportation cost and transportation time of long and bulky cargo; The transportation cost and time of the long and bulky cargo transported by the reuse planning route compared to road-railway multimodal transportation route is reduced by 10.6%, 26.0%, and the BCR can reach 1.261 6.

transportation planning; route reuse planning; multimodal transportation; genetic algorithm; transportation network design problem (TNDP); transportation corridor

U116.2

A

1672 − 7029(2019)07− 1810 − 10

10.19713/j.cnki.43−1423/u.2019.07.027

2018−10−13

国家自然科学基金资助项目(71771218，71501190)

雷定猷(1958−)，男，湖南浏阳人，教授，从事交通运输营运管理及优化研究；E−mail：ldy_csu@outlook.com

(编辑 蒋学东)