注浆饱满度对隧道管棚力学特性影响的试验研究
石钰锋,郭杰森,耿大新,闵世超
注浆饱满度对隧道管棚力学特性影响的试验研究
石钰锋1,郭杰森1,耿大新1,闵世超2
(1. 华东交通大学 土木建筑学院,江西 南昌 330013;2. 中国铁路西安局集团有限公司,陕西 西安 710054)
针对隧道管棚存在的注浆不饱满问题,采用室内试验手段对4种注浆饱满度(100%,90%,80%和50%)的注浆管棚进行轴压和纯弯试验,并采用数值分析手段对试验管棚的力学性能进行了模拟。研究结果表明:随着注浆饱满度降低,注浆管棚的极限弯矩和弹性模量均明显降低。当注浆饱满度为90%时,管棚试件的极限弯矩下降幅度为20.6%,弹性模量降幅为23.8%;当注浆饱满度为80%时,极限弯矩下降幅度达到29.4%,弹性模量降幅为41.6%;当注浆饱满度为50%时,极限弯矩下降41.2%,弹性模量仅为注浆饱满情况的1/3左右。根据试验所得的弹性模量值,采用有限元软件对试件进行模拟分析,计算所得试件的荷载-纵向变形曲线和弯矩-挠度曲线与试验结果基本吻合,验证了试验结果的准确性。
隧道管棚;注浆饱满度;力学特性;室内试验

注浆管棚作为隧道及地下工程施工中一种重要的预支护(加固)手段,能够防止围岩坍塌、控制地层位移和提高围岩力学参数,因其传递荷载作用明显、工艺简单、施工便捷、造价低等特点,在工程界应用广泛[1−2]。在工程中因浆液材料、工艺控制及施工质量等原因,难以避免出现注浆欠饱满的情况,该缺陷给其预支护效果带来不确定性。目前,国内外针对此问题的研究尚未见文献报道,部分学者针对钢管混凝土填充不饱满的问题进行了研究,可供隧道预支护管棚注浆不饱满问题的探讨提供思路。叶跃忠等[3−5]通过试验,对钢管混凝土结构出现钢管与混凝土之间脱开前后进行对比研究,结果表明两者脱开后随着裂缝宽度增大,力学性能急剧损失,严重影响结构的安全,但脱开后进行二次灌浆达到饱满,力学性能基本恢复。Dundu[6]通过制作试验对钢管直径、构件长度、混凝土材料及浆液填充饱满程度4种参数对于圆钢管混凝土性能的影响进行研究。结果发现:钢管混凝土长柱主要破坏方式为整体弯曲,而钢管混凝土破坏的主要原因是混凝土被压碎钢管屈服。Farid等[7]结合轴压试验及ABAQUS有限元软件对混凝土填充率与钢管混凝土的承载力进行分析,将试验结果、规范计算结果以及有限元软件结果对比分析,发现大部分规范计算所得的承载力较为保守。YUAN等[8]进行圆形部分填充钢管混凝土柱的单向、双向往复荷载试验,结果表明:在较低的混凝土填充率时,双向作用比单向作用安全性更差。王军等[9]对实验室钢管混凝土进行了非线性振动特性分析,结果表明钢管混凝土非线性振动特性受其界面作用影响,在未发生加载脱黏的情况下,混凝土浇筑质量不良将削弱其界面的胶结作用,使得构件的非线性特性远小于浇筑良好的钢管混凝土构件。王占飞等[10−11]通过试验研究对比分析不同混凝土填充率钢管混凝土的抗震性能,结果表明混凝土填充率过低,钢管会在填充混凝土的上方发生局部失稳破坏,混凝土填充率越高,钢管的抗震性能越好。近年来,业内研究多集中于注浆管棚预支护效果的定性分析及数值手段探讨规律方面,少见试验手段的定量分析,为此本文通过系列室内试验手段研究注浆饱满度对注浆管棚力学特性的影响,可望为管棚预支护效果评价乃至设计提供借鉴。
1 试验方案及过程
1.1 试验方案
根据既有研究[12]及工程经验,软弱围岩管棚预支护中管径多采用φ108,本文选取该直径管棚开展研究,主要讨论饱满度分别为100%,90%,80%和50% 4种工况(见表1),每种工况分别开展轴压试验和纯弯试验。试验试件采用Q235钢管,管长900 mm,管内填充M30水泥砂浆,为贴合现场施工采用与实际施工相同配比(水泥:砂浆:水=1:0.5:0.45)。每种工况各2根试件,一共8根。试件形式如图1所示。

图1 试件尺寸及剖面示意图
1.2 试样制作
参考国内外学者在钢管混凝土柱的试验研究方法,按照试验方案制成φ108钢管柱8根,并依照表1进行编号标记。所有试件所用材料一致,同一批次制作,制作过程如下:选取对应编号直径为108 mm的钢管共8根,分为2组。灌注之前先将钢管柱的底部用预制圆钢片封口,再用塑料薄膜纸固定,然后将钢管柱放置在水平钢板上固定,通过漏斗将砂浆从上部端口按照饱满程度体积比例注入钢管柱内部,如图2。

表1 工况及材料参数表

图2 砂浆灌注平台
灌浆完成后,采用高强环氧砂浆涂抹上部端口及塑料薄膜纸进行封闭。随后将试件水平放置于振动平台上,用固定底座固定,开启振动2~3 min,分别制成饱满程度为100%,90%,80%和50%(如图3)的试件各2个,将试件放入养护室在标准养护条件下养护7 d,随后自然养护20 d,部分试件如图4所示。

图3 试件不同饱满程度剖面示意图
1.3 测点布置
轴压试验主要测量以下2项:1) 采用位移传感器测试件的纵向变形,在压力试验机的上压板处对称布置2个量程为300 mm的位移计以测定整个试件的纵向变形;2) 在管棚试件的四周分别布置应变花,测定试件横向和纵向应变,沿试件外表面长度方向对称布置4条竖线(如图5(a)),在每条竖线4分点上布置应变花(如图5(b)),共计12个测点,以分别测定轴压过程中试件的上、中、下部的横、纵向应变。

(a) 工况2;(b) 工况4

(a) 截面图;(b) 侧面图
纯弯试验测试项目与轴压试验类似,在试件外表面长度方向中心处,环向均匀布置8个应变花(如图6(a)),以测定纯弯试件受拉部分和受压部分的横向和纵向应变。同时,分别在试件的4分点及基座处共布置5个量程为300 mm的位移计以测定各部分的挠度变化值,如图6(b)所示。

(a) 截面图;(b) 侧面图

(a) 示意图;(b) 实物图
1.4 试验装置及加载
轴压试验采用的加载设备为500 t液压试验机,进行一次压缩试验,装置如图7所示。试验采用分级加载模式,当试件变形处于弹性阶段时,每级加载值为预估极限荷载的1/10,当外钢管屈服后,每级加载值调整为预估极限荷载的1/15,每级加载均持荷2 min,试件接近破坏时保持缓慢连续加载,当承载力下降约为极限承载力的60%时卸载,试验结束。
纯弯试验中,考虑到管棚注浆不饱满情况下,试验刚性梁与试件之间为点接触,荷载集中在试件钢管顶部,与现场实际情况不符,因此设计一种U型卡槽,放置于刚性梁与试件之间(如图8),使荷载均匀分布加载在试件上,与现场实际情况一致。采用加载设备为1 000 kN电动油压千斤顶,试件采用分级加载模式,在达到预估极限荷载设计值的90%之前,按照预估极限荷载的1/10分级加载,每级荷载间停2 min左右。之后按预估极限荷载的1/20分级加载,为避免变形过大损坏仪器,当跨中挠度达到/20左右时停止试验,如图9所示。

单位:mm

图9 纯弯装置
2 试验结果分析
2.1 试验现象
图10为轴压试验各试件的破坏形态,可见轴压试件破坏形态基本接近,均是因为受压弯曲破坏。试验开始一段时间后听到内部水泥砂浆受压破碎的声音,随后试件出现小幅度弯曲,试件上端、中部及下端出现鼓曲。对比图10中各类型试件可以发现注浆饱满情况下试件鼓曲,而注浆不饱满时试件钢管出现凹槽,且随注浆饱满度降低凹槽深度加深。

图10 轴压试件整体破坏状态
图11为部分纯弯试件最终破坏形态,可见管棚试件破坏形态与钢管混凝土破坏形态接近。注浆饱满情况下,试件钢管外表面基本未出现局部凸曲现象,曲线光滑,当管棚试件注浆饱满度不足,试件与卡槽接触处出现凹槽,深度随饱满度降低而增大,且两端管口出现变形,由圆形向椭圆发展,管壁与水泥砂浆出现脱开。

(a) 工况1;(b) 工况1;(c) 工况4
2.2 变形规律
当管棚试件出现注浆不饱满时,钢管内填充水泥砂浆出现变形不连续,荷载−纵向变形曲线出现类似台阶状,即弹性阶段减短,塑性阶段增长,且达到极限荷载后,承载力呈线性骤降趋势,3种不同饱满度下-Δ变形曲线形状类似,如图12所示,说明注浆不饱满对管棚试件轴向承载性能有很大的影响。

图12 不同饱满度下管棚试件荷载-纵向变形曲线
试验实测的抗弯承载力ue取钢管受拉区最外缘应变max达0.01时所对应的弯矩值[13]。管棚试件纯弯弯矩u按照《钢管混凝土结构技术规范》(DB 36/J001—2007)中钢管混凝土受弯承载力公式 计算:



式(1)中的sc为管棚试件组合轴压强度设计值,对于圆形截面,按下式进行计算:
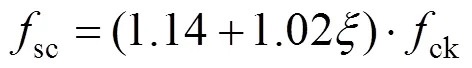
图13为试验实测的不同饱满度下的弯矩−挠度关系曲线,可以看出,所有曲线大致分为3个阶段:弹性阶段、弹塑性阶段以及塑性阶段。在弹性阶段弯矩与挠度呈线性增加关系;弹塑性阶段,弯矩增加较小,挠度增加较大,弯矩−挠度关系曲线斜率越来越小,直至进入塑性阶段;达到塑性阶段后,弯矩略微减小,但挠度仍继续增加。当注浆不饱满时,随着饱满度降低,弹性阶段m关系曲线斜率明显减小,极限弯矩也随之降低,具体表现为:当注浆饱满度为90%时,管棚试件的极限弯矩下降幅度达到20.6%;当注浆饱满度为80%时,管棚试件的极限弯矩下降幅度达29.4%;当注浆饱满度为50%,极限弯矩下降41.2%。

图13 不同饱满度下管棚试件弯矩-挠度曲线
2.3 弹性模量
不同工况下弹性模量测试结果如表2所示。

表2 弹性模量测试结果
注:表中a为按钢管混凝土结构技术规范(DB36/J001—2007)中相关公式计算所得承载力设计值,不饱满度情况下,以注浆面积计算,不考虑饱满度对承载力的影响。
弹性模量根据规范规定的测试取值荷载与测试初荷载的应变差与应力差求得:

式中:Δ为轴压试验所得的应变差;Δ为轴压试验所得的应力差;sc表示试件的横截面面积。
注浆饱满度对于弹性模量的影响结果如图14所示,随着注浆饱满度降低,管棚试件弹性模量迅速降低。管棚注浆饱满度降低到90%时,弹模降幅23.8%;饱满度降低到80%时,弹模降幅41.6%;饱满度降至50%时,弹模降幅60.6%。

图14 弹性模量与注浆饱满度关系曲线
2.4 与数值结果对比
采用数值手段对上述试验进行模拟分析,试件水泥砂浆和钢管网格划分如图15所示,对不饱满部分试件,采用小参数法模拟,即对该部分划分网格,将其参数设为接近于0。

(a) 注浆饱满度100%;(b) 注浆饱满度50%
轴压试验中管棚采用固定边界,限制,和3个方向的位移。模型顶端作为加载位置,不约束。纯弯试验中,在试件模型靠中的2个4分点处,施加方向纵向位移(沿方向60度范围,考虑不饱满情况)。在试件底部距离两端各50 mm处,施加支座约束,左侧约束和方向位移,右侧约束方向位移。
采用ABAQUS有限元软件分别对2根代表性管棚试件(饱满度90%和饱满度50%)建立轴压试验及纯弯试验模型并求解,将模型计算结果与实际试验结果荷载变形曲线和破坏形态进行对比。
通过图16~17的对比可以发现:1) 试件轴向受压(纯弯受压)的有限元计算的荷载−位移曲线(弯矩−挠度曲线)与实际试验曲线基本吻合;2)轴压试验有限元模拟-Δ曲线弹性阶段与试验弹性阶段基本一致,说明试验前期弹性阶段测量结果准确,受试件制作和试验仪器影响较小;3) 纯弯试验有限元模拟结果虽略大于试验结果,但可以看出,随着注浆不饱满度的降低,管棚试件的抗弯承载力明显大幅度下降,与试验结论一致。

(a) 工况2;(b) 工况4

(a) 工况2;(b) 工况4
通过图18~19的对比可以发现:1) 当注浆不饱满时,轴压试验试件的有限元计算结果与试验结果顶部与底部均出现鼓曲,中部均向不饱满侧弯曲;2) 纯弯试验试件的有限元计算结果与试验结果表面均出现类似程度的凹槽;3) 虽然试验试件变形与有限元模拟结果存在些许偏差,但两者变形特征及趋势吻合较好。

图18 轴压试验破坏形态比较

图19 纯弯试验破坏模型比较
由此可见,采用文中的本构关系及参数定义来模拟计算管棚试件的轴向受压、纯弯曲是可行的,通过将两者结果对比,能够互相验证试验与有限元结果的正确性。
3 结论
1) 管棚注浆不饱满会对其抗弯承载性能造成很大的影响,管棚注浆饱满降至90%,极限弯矩降低20.6%;饱满度降至80%,极限弯矩降低29.4%;饱满度降至50%,极限弯矩降低41.2%。
2) 当管棚试件出现注浆不饱满缺陷时,其弹性模量随之降低。在相同长细比下,弹性模量随饱满度的降低而剧烈下降。当管棚注浆饱满度为90%时,弹性模量降低幅度达23.8%;当饱满度为80%时,弹模降幅41.6%;当注浆饱满度为50%时,弹性模量仅为注浆饱满情况的1/3左右。
3) 根据试验结果,采用有限元建模方法能够较好地模拟管棚试件轴向受压和纯弯曲全过程,且其计算所得试件的荷载−位移曲线和弯矩−挠度曲线与试验结果吻合良好。
[1] 石钰锋. 浅覆软弱围岩隧道超前预支护作用机理及工程应用研究[D]. 长沙: 中南大学, 2014: 5−10. SHI Yufeng. Study on mechanism and engineering application of advanced support for lower overburden tunnel in weak stratum[D]. Changsha: Central South University, 2014: 5−10.
[2] SHI Yufeng, FU Jinyang, YANG Junsheng, et al. Performance evaluation of long pipe roof for tunneling below existing highway based on field test and numerical analysis-case study[J]. International Journal of Geomechanics, 2017, 17(9): 1−12.
[3] 叶跃忠. 混凝土脱黏对钢管混凝土中、低长柱性能的影响[J]. 铁道建筑, 2001(10): 2−5.YE Yuezhong. Effect of concrete debonding on the performance of medium and low concrete columns of concrete filled steel tubes[J]. Railway Engineering, 2001(10): 2−5.
[4] 叶跃忠, 李固华, 潘绍伟, 等. 二次灌浆后钢管混凝土性能研究[J]. 公路, 2003(8): 81−84.YE Yuezhong, LI Guhua, PAN Shaowei, et al. Study on the performance of concrete-filled steel tube after second times grouting[J]. Highway, 2003(8): 81−84.
[5] 叶跃忠, 文志红, 潘绍伟. 钢管混凝土脱黏及灌浆补救效果试验研究[J]. 西南交通大学学报, 2004, 39(3): 381−384.YE Yuezhong, WEN Zhihong, PAN Shaowei. Experimental research on separation of concrete-filled steel tube and effect of pouring pulp[J]. Journal of Southwest Jiaotong University, 2004, 39(3): 381−384.
[6] Dundu M. Compressive strength of circular concrete filled steel tube columns[J]. Thin-walled Structures, 2012, 56(4): 62−70.
[7] Farid Abed, Mohammad AlHamaydeh, Suliman Abdalla. Experimental and numerical investigations of the compressive behavior of concrete filled steel tubes (CFSTs)[J]. Journal of Constructional Steel Research, 2013, 80: 429−439.
[8] YUAN Huihui, DANG Ji, Tetsuhiko Aoki. Behavior of partially concrete-filled steel tube bridge piers under bi-directional seismic excitations[J]. Journal of Constructional Steel Research, 2014, 93: 44−54.
[9] 王军, 曹晖. 基于振动特性判别钢管混凝土两种材料间的脱黏规律[J]. 土木建筑与环境工程, 2018, 40(1): 48−54.WANG Jun, CAO Hui. Discriminant analysis of debonding of CFST based on nonlinear vibration characteristics[J]. Journal of Civil, Architectural & Environmental Engineering, 2018, 40(1): 48−54.
[10] 王占飞, 隋伟宁, 赵中华, 等. 带有横隔板补强的部分填充圆形钢管混凝土桥墩柱抗震性能研究[J]. 建筑结构学报, 2013, 34(增1): 233−239.WANG Zhanfei, SUI Weining, ZHAO Zhonghua, et al. Study on seismic performance of partially concrete-filled steel circular bridge piers with transverse diaphragm[J]. Journal of Building Structures, 2013, 34(Suppl 1): 233− 239.
[11] 王潇宇, Cristoforo Demartino, 徐金俊, 等. 侧向冲击作用下钢管混凝土柱动力响应试验研究及计算方法[J]. 土木工程学报, 2017, 50(12): 28−36.WANG Xiaoyu, Cristoforo Demartino, XU Jinjun, et al. Dynamic response of concrete filled steel tube column under lateral impact load: experimental study and calculation method[J]. China Civil Engineering Journal, 2017, 50(12): 28−36.
[12] 苟德明. 既有公路下连拱隧道管棚变形测试与作用机理研究[D]. 长沙: 长沙理工大学, 2007: 3−8. GOU Deming. Deformation test and working mechanism research of pipe-roof in double-arch tunnel under the existing highway[D]. Changsha: Changsha University of Science & Technology, 2007: 3−8.
[13] 于清, 陶忠, 陈志波, 等. 钢管约束混凝土纯弯构件抗弯力学性能研究[J]. 工程力学, 2008(3): 187−193. YU Qing, TAO Zhong, CHEN Zhibo, et al. Flexural behavior of steel tube confined concrete members under pure bending[J]. Engineering Mechanics, 2008(3): 187− 193.
Experimental research on effect of grouting plumpness on mechanical properties of tunnel pipe roof
SHI Yufeng1, GUO Jiesen1, GENG Daxin1, MIN Shichao2
(1. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China; 2. China Railway Xi’an Bureau Group Co., Ltd, Xi’an 710054, China)
Aiming at the problem of incomplete grouting in tunnel pipe roof, laboratory tests for grouting pipe roof under four different grouting plumpness (100%, 90%, 80%, 50%) were used to carry out axial compression test and pure bending test, and numerical analysis were used to simulate the mechanical properties of the test pipe roof. The results show that, incomplete grouting has great influence on the mechanical properties of pipe roof, with the decrease of grouting plumpness, the ultimate bending moment and elastic modulus decrease obviously. When the grouting plumpness is 90%, the ultimate bending moment of the pipe roof specimens is decreased by 20.6% and the elastic modulus is decreased by 23.8%; When the grouting plumpness is 80%, the ultimate bending moment is decreased by 29.4% and the elastic modulus is decreased by 41.6%; When the grouting plumpness is 50%, the ultimate bending moment is decreased by 41.2% and the elastic modulus is only about one-third of full grouting condition. According to the elastic modulus value obtained from the test, finite element software was used to model and analyze the specimens. The calculated load-longitudinal deformation curve and bending moment-deflection curve of finite element method are relatively consistent with the experimental results. The accuracy of the experimental results is verified.
tunnel pipe roof; grouting plumpness; mechanical properties; laboratory test
TU921
A
1672 − 7029(2019)07− 1735 − 08
10.19713/j.cnki.43−1423/u.2019.07.018
2018−09−06
国家地区科学基金资助项目(51768020);国家自然科学基金地区基金资助项目(51568022);江西省交通运输厅科技资助项目(2016D0039)
耿大新(1977−),男,山东济南人,副教授,博士,从事隧道与岩土介质相互作用研究;E−mail:gengdaxin@ecjtu.edu.cn
(编辑 阳丽霞)

