高速铁路无砟轨道扣件弹条断裂原因分析

向俊，袁铖，余翠英, 2，林士财，杨海明

高速铁路无砟轨道扣件弹条断裂原因分析

向俊1，袁铖1，余翠英1, 2，林士财1，杨海明1

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 华东交通大学 理学院，江西 南昌 330013)

为研究高速铁路无砟轨道扣件系统中的弹条部件断裂原因，以WJ-7型扣件为研究对象，建立扣件系统有限元实体模型，分析扣件安装、车轮多边形磨耗及曲线线型等3种条件下的扣件弹条力学特征。研究结果表明：预紧力到24 kN时扣件安装到位，即使无其他荷载作用，弹条本身就已存在相当大的应力值，过拧将继续增大应力值；车轮多边形磨耗阶数的提高会增大弹条应力值，3阶磨耗时应力增量36 MPa，较无磨耗增大5倍，疲劳寿命较无磨耗状态降低95%；曲线半径减小和车速提高将增大弹条应力，降低其疲劳寿命，其中半径影响更显著，半径4 000 m时弹条寿命2万次，较8 000 m减少98%以上。本文可为扣件的养护维修提供参考。

高速铁路；无砟轨道；扣件；弹条；断裂

扣件系统在高速铁路轨道结构中发挥着保证轨道正确几何形位的重要作用，它固定钢轨，阻止其发生纵向和横向位移[1]。扣件弹条承受列车反复荷载作用下造成的拉压、弯曲、扭转和剪切等复合作用，一旦发生断裂，将直接威胁高铁行车安全。国内外学者对扣件进行了大量研究。Dalibor等[2]从扣件系统的安装角度分析SKL-1型弹条的静力学特性，针对扣件设计和安装提出了相应优化措施；Casado等[3]结合扣件材料的种类和属性等方面，研究弹条断裂原因；伍曾等[4]基于离散裂缝模型，模拟弹条裂纹，验证了微动磨损对弹条断裂的影响。关于弹条动力学方面的研究，Mohammad等[5]分析不同紧固条件下，扣件模态和刚度等变化；WANG等[6−7]探究钢轨波磨对弹条动力性能的影响，发现由波磨导致的钢轨振动幅值增大，将造成扣件弹条伤损；余自若等[8]分析单一的X2型弹条在不同扣压力作用下的疲劳性能，从荷载和频率等方面探究降低弹条寿命的原因；肖宏等[9]建立e型弹条计算模型，通过分析弹条模态振型、谐响应特征等，从时频域角度，探究其断裂的原因。我国高速铁路运营实践表明，无砟轨道扣件系统在服役期，曾出现弹条断裂现象，虽然未引起安全事故，但是，为高铁运管部门敲响了警钟，曾一度引起了科研人员的高度重视。因此，本文研究具有重要理论及工程意义。既有文献多从材料、扣压力及轨道波磨等角度对扣件弹条断裂原因进行分析。随着研究的推进，关于车轮多边形磨耗、车速、曲线线形和疲劳寿命等复杂因素及条件下扣件弹条疲劳和断裂影响的量化分析，有待深入研究。鉴于WJ-7型扣件是我国高速铁路无砟轨道扣件的主要类型之一，本文以其为研究对象，采用Abaqus有限元软件，建立扣件精细化分析模型，考虑扣件安装、车轮多边形磨耗、车速及曲线线型等多种条件，分析无砟轨道扣件弹条的力学特征及疲劳影响，为探究弹条断裂原因以及工程措施提供依据。

1 计算模型及验证

目前多数文献直接以弹簧和阻尼器代替扣件，或将扣件与轨道结构绑定来分析结构受力，这种模型从轨道结构整体受力分析来说是可行的，但是，对于扣件系统中各部件受力分析来说，则不仅显得简略，而且难以分析扣件系统在安装、运营中的细部受力情况，甚至无法描述弹条的力学特性变化。

本文采用的钢轨−扣件系统包括标准60轨和WJ-7型扣件系统，弹条为理想弹塑性材料，屈服强度取1 600 MPa。基于Abaqus有限元软件，钢轨轨下胶垫采用纵向和横向接地弹簧模拟，刚度均取为30 kN/mm；绝缘块与钢轨之间的接触关系采用非线性接触进行模拟；弹条与绝缘板、螺栓及铁垫板之间均采用面−面接触方式。模型中，钢轨与绝缘板间摩擦因数取值0.3；弹条与绝缘板及铁垫板间的摩擦因数均取为0.3；弹条与螺栓间的摩擦因数取为0.2[8, 10]。铁垫板采用C3D10单元，弹条等其他部件采用C3D8R单元进行划分。所建立的有限元模型如图1所示，各部件材料参数见表1。

(a) 扣件−钢轨模型；(b) 扣件模型；(c) 弹条精细模型

表1 各部件材料参数

边界条件设置：螺栓仅考虑竖向位移；铁垫板底部全约束；弹条中部前端约束沿钢轨纵向位移，防止弹条纵向滑动；钢轨纵向两端面采用对称约束来限值位移。

为了验证有限元模型的准确性，在进行扣件系统安装过程分析时，提取安装到位状态下，扣件弹条的中肢位移及绝缘板上的扣压力，与文献[10−11]以及安装规范进行比对，结果如表2所示。

表2 模型验证

从表2可见，本文模型模拟结果与文献中结果基本一致，数值差小于10%，且符合规范值要求，模型能满足计算分析需要。

2 计算工况与疲劳计算方式

2.1 计算工况与荷载拟定

随车速不断提高，车轮磨损问题时有发生，其中，车轮多边形磨耗是高速列车运营中产生的典型伤损之一。车轮多边形磨耗致使轮轨间冲击荷载增大，造成轮轨振动加剧，增大弹条断裂风险。车轮多边形磨耗如图2所示，且以出现前3阶磨耗情况居多[12]。

考虑车轮多边形磨耗、曲线线型及车速等因素，本文设置如下3种计算工况。

1) 工况1：车轮无多边形磨耗(即正常状态)情况下，列车竖向荷载采用包含振动幅值P和频率ω的正弦函数形式[13]，()0+Psinωt，来模拟列车的振动特性，静轮重0取为63 kN，同时考虑车速变化的具体加载时间(取1个荷载周期内)的历程曲线如图3所示。

图2 车轮多边形磨耗示意图

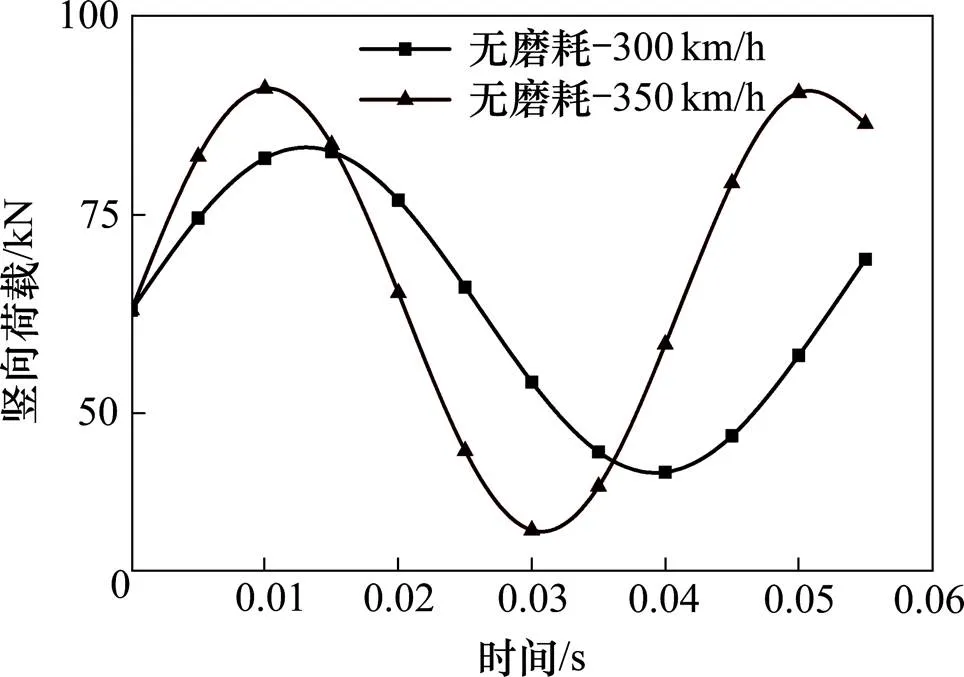
图3 工况1加载时间历程

2) 工况2：分析车轮多边形磨耗对扣件弹条受力影响时，考虑比较常见的前3阶车轮多边形磨耗即可。其中，1阶多边形亦为车轮偏心磨耗，偏心距取为1 mm；2阶多边形磨耗为车轮椭圆化，椭圆度取为1 mm；3阶磨耗引起轮轨系统产生周期性强迫振动。参考文献[12, 14]成果，与1阶、2阶及3阶多边形磨耗分别对应，同时考虑车速变化的轮轨竖向荷载时间(1个周期内)历程曲线如图4所示。

3) 工况3：当列车通过曲线轨道时，钢轨除了承受轮轨竖向作用力外，还会承受比较显著的横向作用力，钢轨将发生横向位移现象，弹条应力增幅将更加显著。根据文献[15]中的研究成果，得出的曲线半径与横向力对应数据如表3所示。在具体加载设置时，轮轨竖向力采用图3模式，且施加于钢轨顶部；轮轨横向力采用表3中的数据，且垂直于钢轨施加于钢轨侧面。

(a) 与1阶多边形磨耗对应的加载时间历程 (b) 与2阶多边形磨耗对应的加载时间历程 (c) 与3阶多边形磨耗对应的加载时间历程

2.2 疲劳寿命计算方式

服役期间的扣件弹条，一般不会因单次荷载较大而断裂，而是由于列车高速运行中弹条承受长期、频繁荷载导致材料疲劳寿命降低而发生破坏。因此，为了探究扣件弹条断裂原因，还需分析弹条在列车动荷载作用下的疲劳寿命。首先需要知道材料的疲劳荷载应力幅值与疲劳寿命之间的关系(即S-N曲线)，根据弹条材料60Si2MnA相关特性和强度极限，参考文献[8]研究成果，其S-N曲线可用如下公式进行描述：

式中：为疲劳寿命，次；−1为循环应力幅值，−1=(max−min)/2，其中，max和min分别为最大、最小应力值，MPa。

表3 曲线轨道轮轨横向力数据

注意到与式(1)对应的S-N曲线仅仅考虑等幅值对称荷载下的应力幅值大小。在实际运营过程中，弹条往往处于拉压、弯扭组合的复杂应力状态下。因此，采用该公式计算存在一定的误差，需考虑弹条平均应力条件对式(1)进行修正。在实际工程中，常采用Goodman模型[16]，基于平均应力对材料疲劳应力幅值进行修正，该模型具有简便且易于计算的优点，本文采用其进行修正：

式中：为应力幅值；−1为修正后的应力幅值；m为平均应力，m(max+min)/2；b为材料的抗拉极限强度，本文弹条材料的抗拉极限强度取值为1 670 MPa。

3 计算结果及其分析

3.1 扣件安装时弹条应力分析

扣件弹条应力来自安装时存在的应力及车辆荷载等导致的应力增量，须先分析扣件安装过程中弹条应力状态。模型中通过在螺栓顶面加载竖向预紧力来实现扣件安装，参照安装规范，中肢下颚接触绝缘块，总扣压力大于9 kN时表示安装到位。图5(a)与图5(b)分别表示扣件安装过程中，弹条扣压力和弹条等效应力随螺栓预紧力的变化曲线。

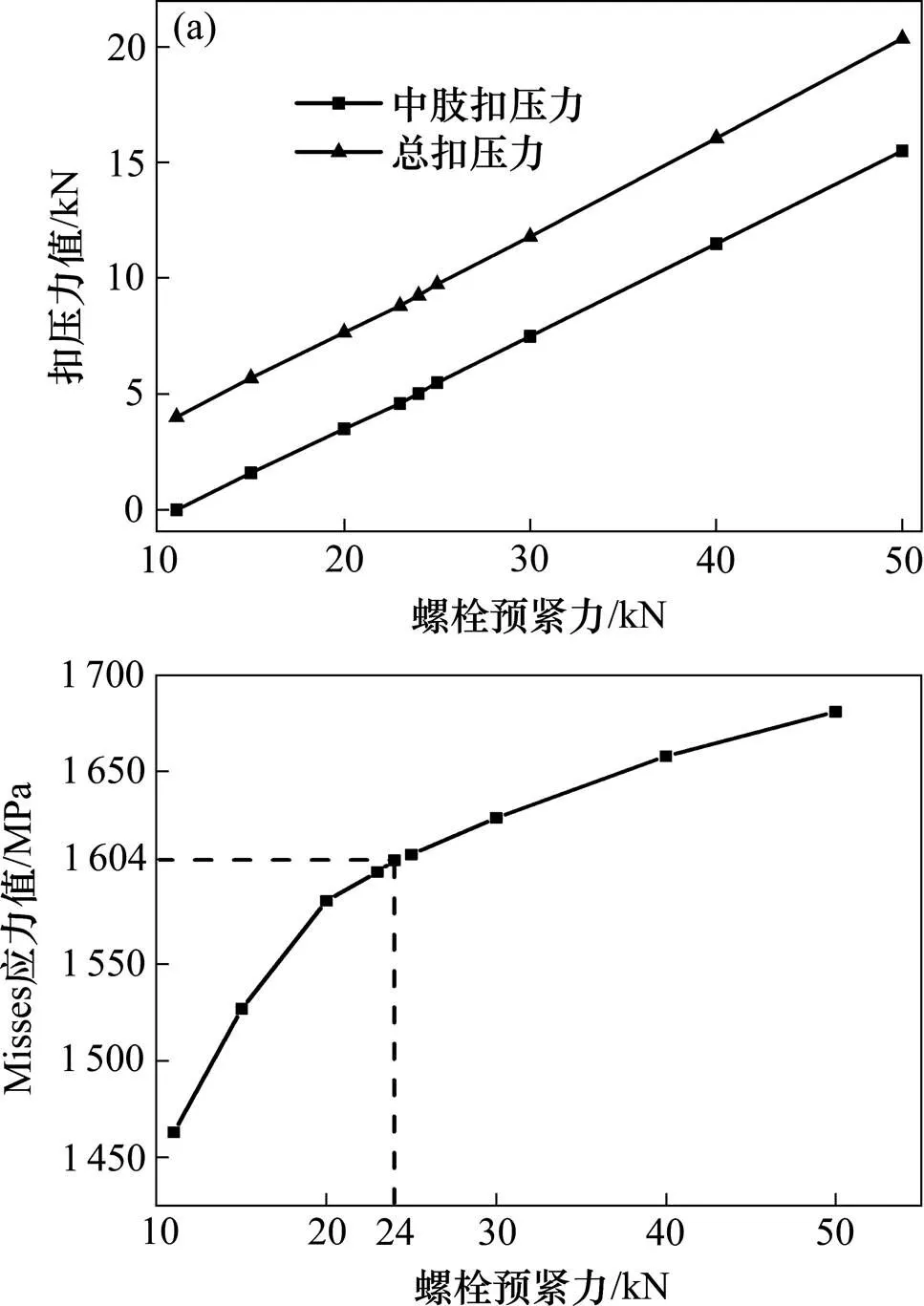
(a) 弹条扣压力；(b) 弹条等效应力

从图5(a)可知，扣件螺栓预紧力与总扣压力呈线性关系。当螺栓顶部加载约11 kN预紧力时，弹条的中肢下颚开始接触绝缘板，产生中肢扣压力。扣件的总扣压力为中肢扣压力和趾端扣压力之和。当预紧力大于24 kN时，总扣压力大于9 kN，满足扣件的安装合格要求。

采用第四强度理论来分析弹条的等效应力，由图5(b)可知，当螺栓预紧力由11 kN增大到20 kN时，弹条表面最大应力值迅速增大，达到弹条材料的屈服强度1 600 MPa；之后随预紧力的增大，应力值增速变缓，这是由于弹条表面发生屈服现象导致弹条产生塑性形变，应力增长变慢。当预紧力达到24 kN时，弹条最大应力值为1 604 MPa，略微超过屈服强度，实际安装过程中是允许的，能够充分利用材料性能，这与文献[11]中的结论一致。当扣件满足安装要求时，弹条本身应力已接近或达到材料屈服极限，此时，在实际运营中，但凡进一步增大弹条应力的因素，均有可能导致弹条跟端、应力集中区域产生裂纹，从而诱发弹条的断裂。有关弹条的应力分布如图6所示，由图6可见，最大应力区域出现在弹条后跟端与铁垫板接触的区域A处，在现场发现的断裂弹条的断裂处，往往也出现在A区域。

图6 扣件安装时弹条应力云图

3.2 车轮多边形磨耗对弹条应力影响分析

按照工况1进行加载，分析车轮无磨耗状态下弹条应力，其等效应力分布见图7。当车速为350 km/h时，弹条等效应力值为1 615 MPa，略大于弹条屈服强度。可见，无车轮磨耗时，列车竖向荷载作用导致的弹条应力增量较小，应力集中区域主要在弹条后端与铁垫板接触区域内弯处。

按照工况2进行加载，计算车轮处于不同多边形磨耗条件下的弹条应力值，有关应力分布见图8。为了更为直观地分析车轮多边形磨耗对弹条应力的影响规律，现在仅考虑在扣除弹条安装应力(1 604 MPa)之后的应力增量值，车轮不同阶数多边形磨耗状态下的弹条应力值及其增量见表4。

综合图8和表4可得出如下结论：

1) 相较无磨耗状态，车轮磨耗明显增大了弹条应力值。在车速一定的情况下，随车轮多边形磨耗阶数的提高，弹条应力增大。例如，车速为300 km/h时，3阶磨耗下弹条应力增量32 MPa，较无磨耗时提高了5倍以上。

(a) 车速−300 km/h；(b) 车速−350 km/h

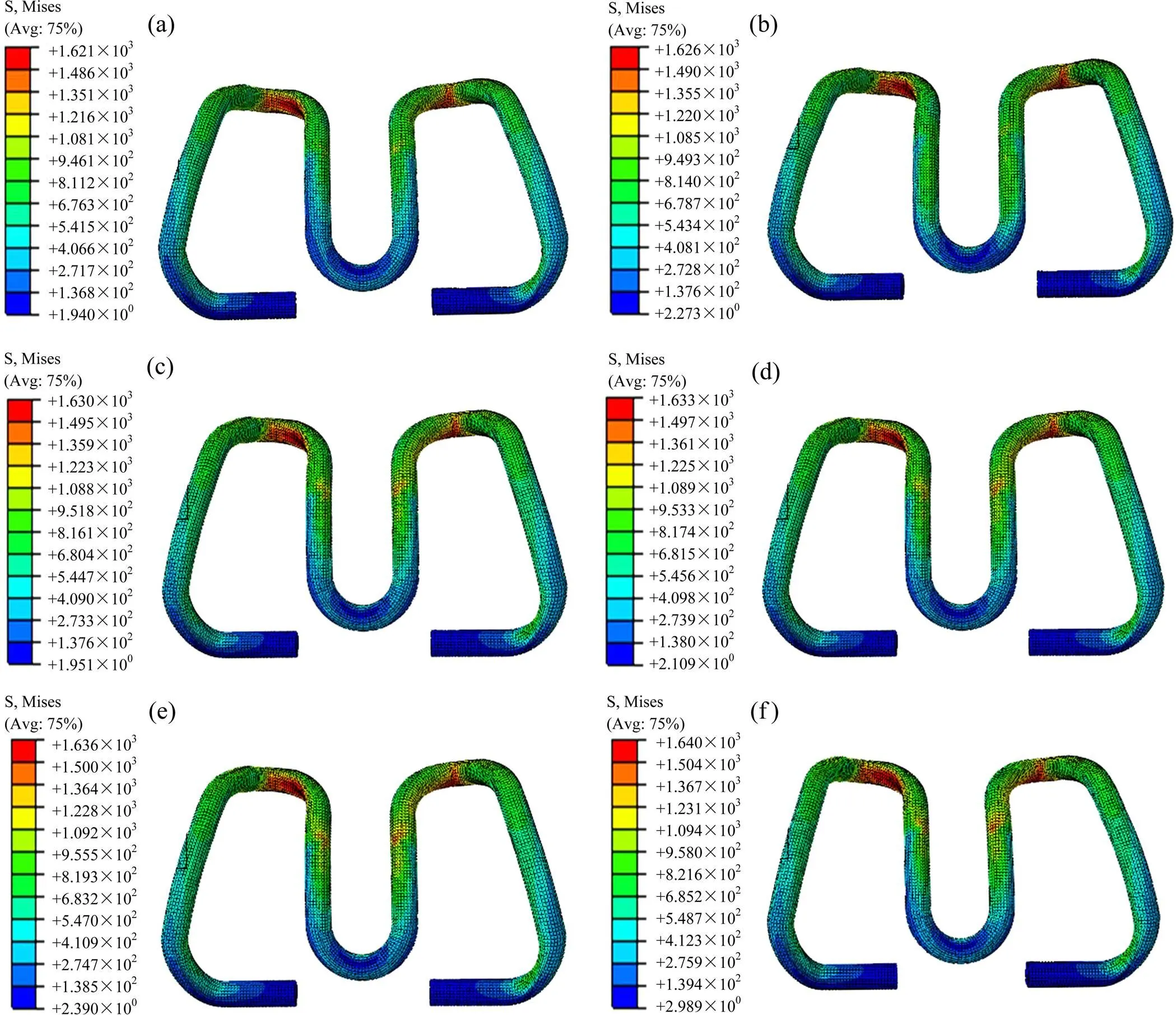
(a) 1阶磨耗−300 km/h；(b) 1阶磨耗−350 km/h；(c) 2阶磨耗−300 km/h； (d) 2阶磨耗−350 km/h；(e) 3阶磨耗−300 km/h；(f) 3阶磨耗−350 km/h

表4 弹条应力增量

2) 相同的车轮磨耗阶数下，随着车速提高，弹条应力值增大，例如，在3阶磨耗状态下，车速350 km/h对应的弹条增量值为36 MPa，车速300 km/h对应的量值增大了12.5%。

3) 车轮多边形磨耗的存在，在一定程度上增大了弹条应力幅值，且随着车速的提高，弹条应力幅值得到了进一步增大，高应力状态下弹条表面更容易出现裂纹。因此，可以说车轮多边形磨耗是高速铁路出现弹条断裂的重要诱因之一。

3.3 曲线半径及车速对弹条应力影响分析

按照工况3进行加载，计算列车以不同车速通过不同半径曲线轨道时的扣件弹条应力，分析曲线半径及车速对弹条应力的影响规律。计算时发现弹条应力集中区域的分布类似于直线路段，主要分布于同铁垫板接触的跟端区域。有关扣除安装应力之后的弹条最大等效应力增量随线路曲线半径及车速的变化趋势如图9所示。

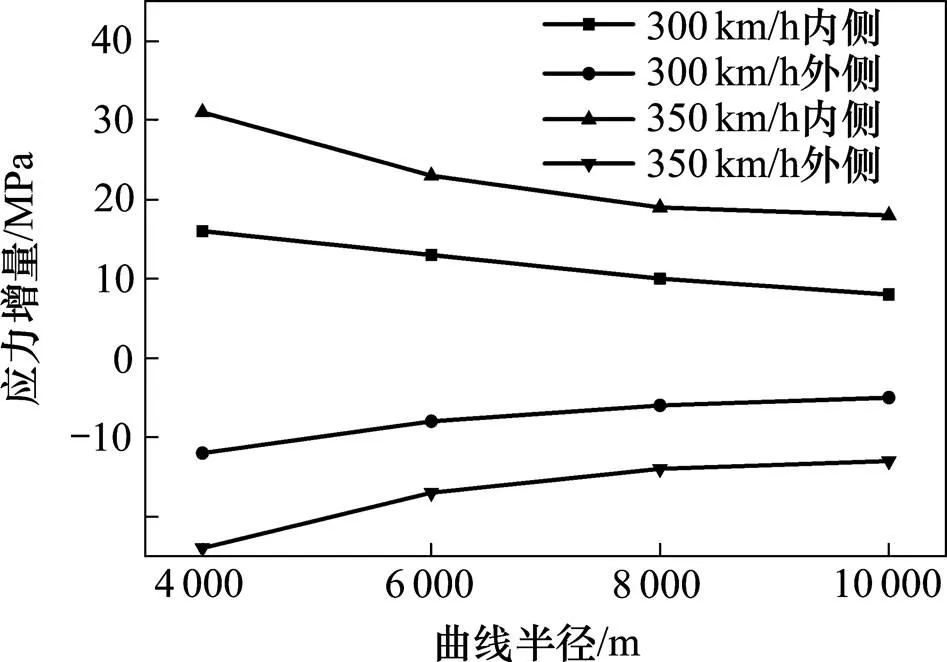
图9 曲线半径对弹条应力影响

由图9可见：

1) 随着曲线半径的增大，内侧弹条等效应力增量呈现下降趋势，而外侧的应力则呈增大趋势，两侧的应力值均向弹条安装应力接近，但内侧的应力不仅高于外侧相应的应力，且始终高于材料屈服强度，内侧最大增量30 MPa。外侧应力则低于屈服 强度。

2) 当曲线半径一定时，曲线内侧的弹条应力增量随车速的提高而增大。

3) 当列车通过曲线轨道时，随着曲线半径的减小及运行速度的提高，将直接引起轮轨间横向力增大，导致钢轨发生一定程度的偏转，内侧轨底抬升上拔扣件弹条，使得弹条跟端与铁垫板的接触挤压程度加剧，增大内侧弹条的最大应力值，内侧弹条表面产生裂纹的可能性更大，在车辆反复荷载作用下更容易断裂。此分析结果与现场资料中弹条断裂区域及位置相符。

3.4 弹条疲劳寿命分析

3.4.1 车轮多边形磨耗对弹条疲劳寿命的影响分析

虽然车轮多边形磨耗的存在大大提高了弹条应力幅值，但是，并非一旦在车轮多边形磨耗作用下，弹条就马上断裂。事实上，必须在列车反复作用下，才有可能在跟端区域发生疲劳破坏。为此，根据上述式(1)与式(2)，在弹条跟端应力集中区域选取5个节点进行疲劳寿命分析，如图10所示。

由图10可见：

1) 在车速一定时，相对车轮无磨耗状态而言，车轮多边形磨耗的存在明显降低了弹条疲劳寿命，且随着车轮磨耗阶数的增大，弹条疲劳寿命逐渐减小。

2) 在车轮出现3阶磨耗的情况下，当车速为350 km/h时，所对应的弹条疲劳寿命次数64万次，较300 km/h时减少了88.5%，且低于设计要求的500万次。

3) 车轮多边形磨耗会导致弹条疲劳寿命降低，且多边形磨耗存在情况下，车速增大将显著降低弹条寿命，导致疲劳破坏。

3.4.2 曲线半径及车速对弹条疲劳寿命的影响分析

同样地，虽然曲线半径及车速对弹条应力影响很大，但是，并不是说，高速列车一旦通过曲线轨道，曲线内侧的弹条就会马上断裂，必须在列车反复作用下，才有可能发生弹条疲劳破坏。图11表示不同曲线半径条件下，两侧弹条跟端最不利位置处的疲劳寿命分析结果。

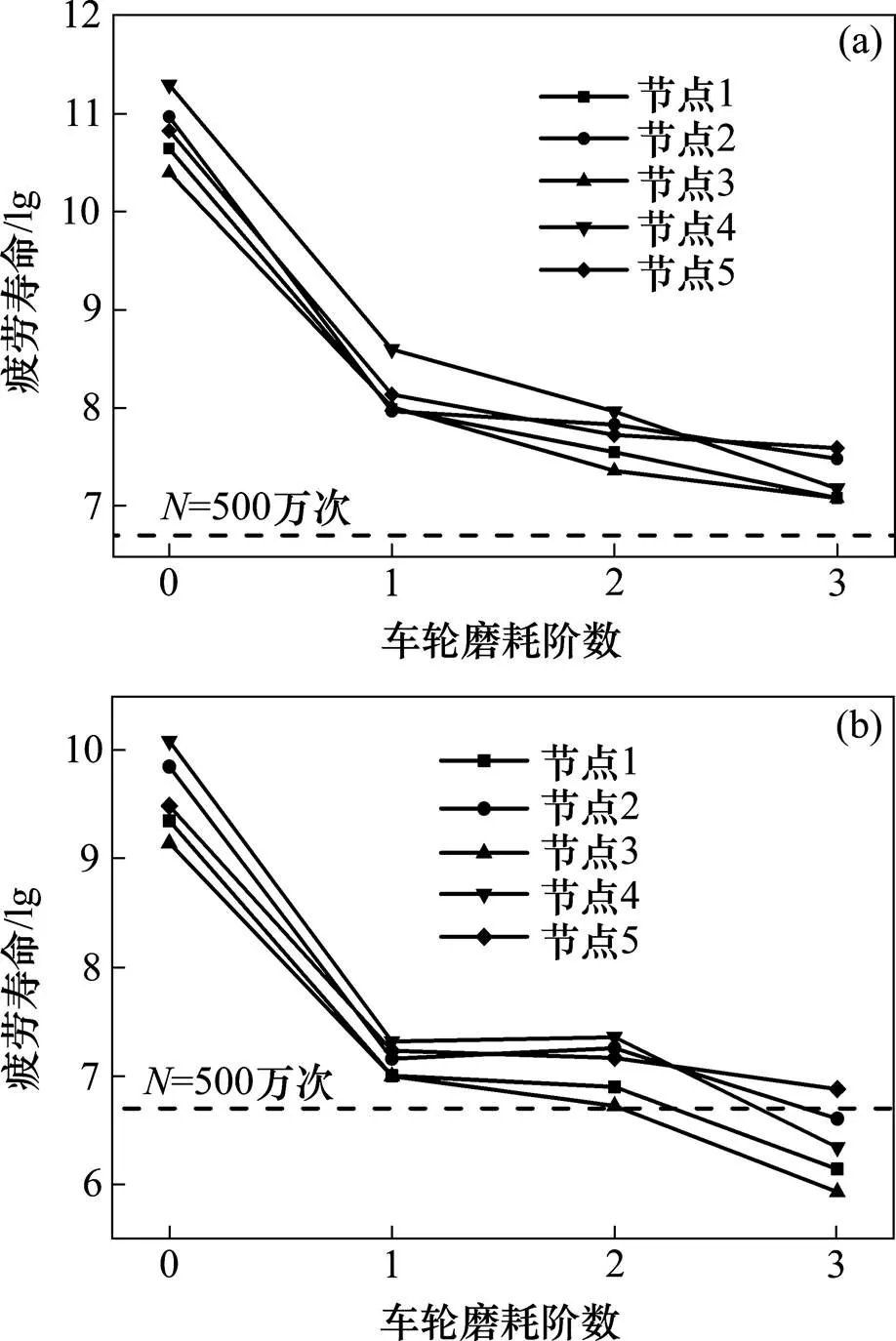
(a) 车速300 km/h；(b) 车速350 km/h

图11 曲线半径及车速对弹条疲劳寿命影响

由图11可见：

1) 外侧扣件弹条疲劳寿命随曲线半径的减小而减小，但始终高于设计要求。

2) 随着曲线半径的减小，内侧弹条疲劳寿命降低更为明显，车速350 km/h，半径小于7 000 m时，弹条疲劳寿命最少仅2万次，不满足设计要求。

3) 线路曲线半径减小及列车车速的增大，均会显著减小内侧弹条的疲劳寿命，提高弹条跟端的应力集中区域发生疲劳断裂的可能性。

4 结论

1) 预紧力达到24 kN时，扣件安装到位，即使无其他荷载作用，弹条内就已经存在了相当大的应力值，超过材料的屈服强度1 600 MPa，并且最大应力出现在弹条后跟端区域。

2) 与正常情况相比，前3阶车轮多边形磨耗状态下，最大应力增量近40 MPa，是无磨耗状态的6倍。车轮磨耗增大了弹条跟端与铁垫板的挤压程度，进一步提高了扣件弹条的应力值。

3) 曲线路段由于轮轨横向力，钢轨内外侧弹条应力变化趋势相反。半径的减小和车速的提高均会增大内侧弹条应力值，跟端处最大应力1 634 MPa，弹条表面屈服程度加剧，进而可能产生裂纹。

4) 车速的提高，车轮多边形磨耗程度的增大及曲线半径的减小，均会降低弹条疲劳寿命。3阶多边形磨耗状态下，弹条寿命为64万次，较无磨耗状态减少95%以上，不足500万次设计要求。危险区域处于弹条与铁垫板接触处，与现场弹条断裂位置基本一致。

[1] 陈秀方, 娄平. 轨道工程[M]. 北京: 中国建筑工业出版社, 2017. CHEN Xiufang, LOU Ping. Track engineering[M]. Beijing: China Architecture & Building Press, 2017.

[2] Dalibor Bartos, Stjepan Lakusic, Tomislav Vinski. Numerical analysis of rail fastening spring clip type SKL-1. 22nd DANUBIA-ADRIA[C]// Symposium on Experimental Methods in Solid Mechanics Parma: University of Parma, 2005: 119−120.

[3] Casado J A, Carrascal I, Polanco J A, et al. Fatigue failure of short glass fibre reinforced PA6.6 structural pieces for railway track fasteners[J]. Engineering Failure Analysis, 2006, 13(2): 182−197.

[4] 伍曾, 李洁青, 黄伟, 等. 微动磨损对弹条Ⅱ型扣件弹条断裂的影响分析[J]. 昆明理工大学学报(自然科学版), 2013, 38(6): 43−47. WU Zeng, LI Jieqing, HUANG Wei, et al. Effect of fretting wear on fracture of type II fastener elastic bar[J]. Journal of Kunming University of Science and Technology (Natural Science Edition), 2013, 38(6): 43− 47.

[5] Mohammad Valikhani, Davood Younesian. Application of an optimal wavelet transformation for rail-fastening system identification in different preloads[J]. Measurement, 2016, 82: 161−175.

[6] WANG Wenbin, WU Zongzhen, LIU Li, et al. Analysis of t-bolts abnormal fracture of DTⅥ2 fastener based on metro pass-by dynamic monitoring[J]. Procedia Engineering, 2017, 199: 2753−2758.

[7] XIAO Hong, WANG Jiabin, ZHANG Yanrong. The fractures of e-type fastening clips used in the subway: Theory and experiment[J]. Engineering Failure Analysis, 2017, 81: 57−68.

[8] 余自若, 袁媛, 张远庆, 等. 高速铁路扣件系统弹条疲劳性能研究[J]. 铁道学报, 2014, 36(7): 90−95. YU Ziruo, YUAN Yuan, ZHANG Yuanqing, et al. Fatigue properties of elastic bars of fastening systems installed with high-speed railways[J]. Journal of the China Railway Society, 2014, 36(7): 90−95.

[9] 肖宏, 马春生, 郭晓, 等. e型扣件弹条断裂原因频谱分析[J]. 同济大学学报(自然科学版), 2017, 45(7): 1000−1008. XIAO Hong, MA Chunsheng, GUO Xiao, et al. Fractures of e-type fastening clip by spectral analysis method[J]. Journal of Tongji University (Natural Science), 2017, 45(7): 1000−1008.

[10] 张树峰. 无砟轨道扣件系统力学性能分析[D]. 成都: 西南交通大学, 2016. ZHANG Shufeng. Analysis on fastening force of ballastless track[D]. Chengdu: Southwest Jiaotong University, 2016.

[11] 罗耀波. 高速铁路WJ-7扣件静、动力分析研究[D]. 昆明: 昆明理工大学, 2017. LUO Yaobo. Static and dynamic analysis of high speed railway WJ-7 fastening[D]. Kunming: Kunming University of Science and Technology, 2017.

[12] 袁雨青. 高速列车车轮不圆机理及影响研究[D]. 北京: 北京交通大学, 2016. YUAN Yuqing. Study on the mechanism and influence of the wheel out-of-round of high speed train[D]. Beijing: Beijing Jiaotong University, 2016.

[13] 梁波, 罗红, 孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报, 2006, 28(4): 89−94. LIANG Bo, LUO Hong, SUN Changxin. Simulated study on vibration load of high speed railway[J]. Journal of the China Railway Society, 2006, 28(4): 89−94.

[14] 尹振坤, 吴越, 韩健. 高速列车车轮多边形磨耗对轮轨垂向力的影响[J]. 铁道学报, 2017, 39(10): 26−32. YIN Zhenkun, WU Yue, HAN Jian. Effect of polygonal wear of high-speed train wheels on vertical force between wheel and rail[J]. Journal of the China Railway Society, 2017, 39(10): 26−32.

[15] 杨星光, 刘永效. 时速350/250 km共线高速铁路曲线半径动力特性研究[J]. 铁道标准设计, 2017, 61(10): 28−32. YANG Xingguang, LIU Yongxiao. On dynamic characteristics of curve radius of shared 350/250 km/h high-speed railway[J]. Railway Standard Design, 2017, 61(10): 28−32.

[16] 陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002. CHEN Chuanyao. Fatigue and fracture[M]. Wuhan: Huazhong University of Science and Technology Press, 2002.

Analysis of elastic bar fracture causes of fasteners in ballastless track of high-speed railway

XIANG Jun1, YUAN Cheng1, YU Cuiying1, 2, LIN Shicai1, YANG Haiming1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. School of Science, East China Jiaotong University, Nanchang 330013, China)

In order to analyze the reasons for the fracture of fastener elastic bar of ballastless track in high-speed railway, the WJ-7 fastener was taken as the research object and a finite element solid model of fastening system was established. Based on the model, the mechanical characteristics of fastener elastic bar in the process of installation, the wheel polygonal wear and the condition of curved line were analyzed. The results show that the fasteners are installed in place when preload is 24 kN, even if there is no other load, the bar itself has a considerable stress value and it increases with over-twisting. Increasing number of wheel polygonal wear order can lead to the raising stress of bar. The third-order wear stress increment is 36 MPa, which is 5 times more than non-wear, and the fatigue life is 95% lower than the wear-free state. When curve radius decreased and speed lifted, it leads to the raise of elastic bar stress and decrease of fatigue life, especially with the influence of radius. The fatigue life of bar is 20 000 times when radius 4 000 m, which is reduced by over 98% compared with radius 8 000 m. This paper can provide reference for maintenance and repair of fasteners.

high-speed railway; ballastless track; fastener; elastic bar; fracture

U213.5

A

1672 − 7029(2019)07− 1605 − 09

10.19713/j.cnki.43−1423/u.2019.07.001

2018−10−15

国家自然科学基金委员会与神华集团有限公司联合资助项目(U1261113)；高等学校博士学科点专项科研基金资助项目(20100162110022)；牵引动力国家重点实验室开放课题资助项目(TPL0901，TPL1214)；江西省教育厅科技资助项目(GJJ151173，GJJ151175)

向俊(1968−)，男，湖南溆浦人，教授，博士，从事列车脱轨控制、列车−轨道(桥梁)系统空间振动及铁路轨道结构等研究；E−mail：jxiang@csu.edu.cn

(编辑 阳丽霞)