Energy distance 的配对样本分布差异检验法
陈敏琼
中山大学新华学院, 广东 广州 510520
配对样本的同分布检验是统计理论及实际中常见的一个基本问题, 通常用于比较同一对象上的两种不同处理或某一处理前后各指标的分布差异. 如对同一研究对象分别给予A,B两种不同处理,记X为处理A下的记录,Y为处理B下的记录,此时要比较两种不同处理的效果差异,就需要对X与Y的分布差异进行显著性检验.再如,如果我们对某个研究对象进行某一处理,若X是未加处理的记录,而Y是施加该处理后的记录, 此时要判断处理是否有效,同样需要对X与Y的分布差异进行显著性检验.
对于配对样本的同分布检验问题,经典的方法有一元t检验法、多元Hotelling T2检验法、符号检验法与Wilcoxcon 符号秩检验法等.一元t检验法与多元Hotelling T2检验法适用于(X,Y)联合分布为二维或多维正态分布情形,且仅是对X,Y的均值差异进行显著性检验.当(X,Y)不满足联合正态的假设,通常我们可用符号检验或Wilcoxcon符号秩检验等非参数检验,但符号检验事实上是检验X-Y分布是否以0为中位数,而Wilcoxcon符号秩检验则检验X-Y分布是否关于0对称显然X与Y同分布并不等价于X-Y分布对称,更不等价于X-Y分布以0为中位数,因而对于配对样本同分布检验而言,符号检验与Wilcoxon检验并不是一致性检验.同时我们应该注意到这些经典方法基本只适用于X与Y为一元随机变量的情形.
Energy distance的概念最早于Székely 与 Rizzo 在文献[1]中提出,它是度量两个独立随机变量分布差异的一个很好的测度,它本质上是两个独立随机向量的分布的特征函数之差的模,但巧妙之处在于通过选取适当的模长定义后它可以表示成距离函数的期望形式,而样本估计只涉及两点之间的距离的计算.因此,作为检验独立样本是否同分布这一基本统计问题,Energy distance提供了一种突破性的方法,它检验的对象可以是任意具有有限维数的随机向量,只需满足有限一阶矩的条件即可.Székely 与Rizzo 在文献[2~6]中分别展示了他们将Energy distance用于处理诸如独立样本同分检验、单样本分布检验、聚类分析、独立性检验、方差分析等一系列经典统计问题的结果[7],对这些方法进行了总结,指出与经典方法相比,这些方法计算简便、适用于更广泛分布类型的数据,且能处理多变量情况.而将 Energy distance 的概念用于配对样本分布的检验则未见有文献提及过.
本文基于独立变量 Energy distance 距离的概念,提出了相关变量的 Energy distance 距离的定义,由此给出一种新的检验配对样本分布差异的检验统计量,并讨论了该检验统计量在两变量同分布的假设下的渐近分布,该检验方法适用于任意有限维数的具有有限一阶矩的随机向量.
1 主要方法与结果
我们先回顾一下文献[1]提出的两个独立的随机变量的Energy distance的定义及主要结果.
定义1[1]设X、Y为取值于Rd的两个独立的随机向量, 并且E|X|+E|Y|<∞,则X与Y的Energy distance 定义为
ε(X,Y):=2E|X-Y|-E|X-X′|-E|Y-Y′|
其中,|.|表示欧氏距离,X′为与X独立同分布的随机变量,Y′为与Y独立同分布的随机变量.

文献[1]给出了命题1的证明, 主要利用到重要的积分等式
(1)
从定义1可以看出, 虽然Energy distance的概念是针对独立变量提出, 但事实上这个概念对于相关变量也可以类似定义. 下面,我们给出相关变量的Energy distance定义,并讨论有关性质.
定义2 设X、Y为取值于Rd的两个相关的随机变量, 假设(X,Y)有联合分布H,边缘分布分别为F,G.假定X,Y都具有有限的一阶矩,即E|X|+E|Y|<∞ 则可定义X,Y之间的Energy distance为
ε(X,Y):=E|X-Y′|+E|Y-X′|-E|X-X′|-E|Y-Y′|
(2)
其中,(X′,Y′)与(X,Y)独立同分布.
与命题1类似,我们有如下等式成立.

(3)
因此,同样有ε(X,Y)≥0并且等号成立当且仅当X与Y同分布.
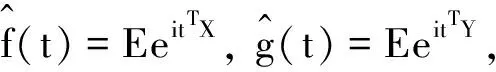
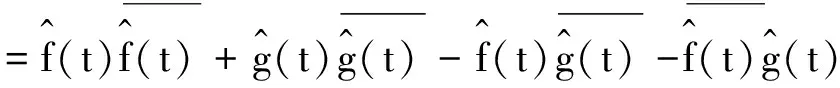
=EeitTXEe-itTX′+EeitTYEe-itTY′-EeitTXEe-itTY′-Ee-itTX′EeitTY
=EeitT(X-X′)+EeitT(Y-Y′)-EeitT(X-Y′)-EeitT(Y-X′)
=1-EeitT(X-Y′)+1-EeitT(Y-X′)-(1-eitT(X-X′))-(1-EeitT(Y-Y′))
等式两边取积分,依据积分等式(1)便可得
因此可得ε(X,Y)≥0并且等号成立当且仅当X与Y具有相同的分布.
推论1 设X与X′为取值为Rd的两个独立同分布的随机向量, 则E|X+X′|≥E|X-X′|且
E|X+X′|=E|X-X′|成立当且仅当X的分布为对角对称.
证明 文献[8,9]分别给出了X为一元随机变量情形的证明, 这里, 我们给出一般性证明,事实上在定义2中令Y=-X可得
ε(X,Y) =ε(X,-X)
=E|X-(-X′)|+E|X′-(-X)|-E|X-X′|-E|-X-(-X′)|
=2(E|X+X′|-E|X-X′|)
因此, 根据命题2的结论, 我们有E|X+X′|≥E|X-X′|,并且E|X+X′|=E|X-X′|成立当且仅当X与-X分布相同,即X的分布为对角对称.
下面我们给出相关变量Energy distance 的样本估计.
定义3 令Wi=(Xi,Yi),i=1,2,…,n为来自(X,Y)的一个样本, 记(X,Y)={W1,W2,…,Wn}, 则X与Y的Energy distance 的样本估计为
(4)
若记
h(w1,w2):=h((x1,y1),(x2,y2))=|x1-y2|+|y1-x2|-|x1-x2|-|y1-y2|
(5)
则εn(X,Y)是一个以h为核的U统计量
(6)
显然εn(X,Y)为ε(X,Y)的无偏估计.
利用U统计量的大样本性质,我们可以得到下面两个关于εn(X,Y)的重要结论.

证明 对于h(W1,W2),在E|X|+E|Y|<∞条件下有,E|h(W1,W2)|≤4(E|X1|+E|Y1|)<∞.同时,由于E[h(W1,W2)]=ε(X,Y),根据文献[10]的结论, 我们有
(7)
定理2 设X、Y为取值于Rd的两个相关的随机变量,(X,Y)有联合分布H,且E|X|+E|Y|<∞,则有
i)若X与Y同分布,则
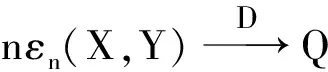
(8)
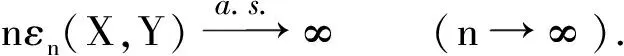
证明 i)若X与Y同分布,则
E[h(W1,W2)]=E|X1-Y2|+E|X2-Y1|-E|X1-X2|-E|Y1-Y2|=0
且
=E|x1-Y2|+E|X2-y1|-E|x1-X2|-E|y1-Y2|=0

这说明εn(X,Y)为一阶退化的U统计量,因此有
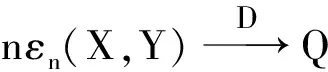
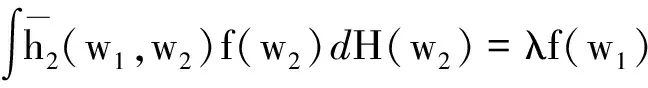
ii)由于当X与Y不同分布时有


2 数值模拟
从上面的结论可知,分布Q依赖于λv,v=1,2,…,而λv一般是不可能得到的,因此我们选用bootstrap 抽样技术来获得检验的p值.注意到H0当成立时,即X,Y同分布时,(X,Y)与(Y,X)具有相同的分布,因此,我们可从样本
Dn={(X1,Y1),…,(Xn,Yn),(Y1,X1),…,(Yn,Xn)}
(9)
其中,εn是原始样本{(X1,Y1),…,(Xn,Yn)}计算得到的检验统计量.
我们考虑以下8个模型:
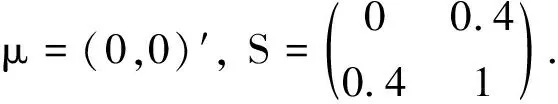
模型2:X~U(0,3),Y=3-X.
模型3:X~B(8,0.5),Y=8-X.
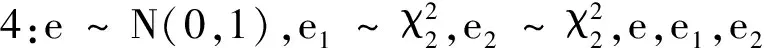
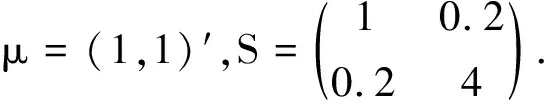

模型7:X~U(0,1),Z~N(0,1),Y=X-Z.

为了说明我们方法的有效性,利用R软件对每个模型分别产生容量为n=30,50,150,100,200的随机样本,对每个模型分别用t检验、Wilcoxon符号秩检验及我们提出的检验方法做比较.表1给出了8个模型的不同容量下三种检验方法的功效,其中p.test指的是本文所提出的检验方法,每次检验基于199次bootstrap重抽样计算p值,三种检验方法的功效是基于1 000次重复试验计算得到.
从模型1到4的模拟结果可以看出,在X,Y同分布的情况下,本文所提出的p.test方法跟经典的t检验法与Wilcoxon符号秩检验法的结果相近,t 检验法与 Wilcoxon 符号秩检验法的第一类错误在 0.05 左右,p.test 的第一类错误在 0.025 附近,因此三种方法都能很好地控制第一类错误.模型4至模型7的结果说明对于X,Y均值相同或X-Y分布对称但X,Y分布不同的情形经典的t检验法与Wilcoxon符号秩检验法都失去了检验功效,而本文所提出的p.test检验法则具有很高的功效.
3 总结
本文基于独立随机向量的Energy distance的概念提出了相关变量的Energy distance 距离的定义,由此给出了一种新的检验配对样本分布差异的检验统计量. 数值模拟结果说明该方法比经典的t检验法与Wilcoxon符号秩检验法能更有效地鉴别出配对变量的分布差异. 该检验方法的检验统计量只涉及两点间的欧氏距离的计算,因此计算非常简便,且适用于任意有限维的具有有限一阶矩的随机向量.

表1 8个模型不同样本容量下三种检验方法的功效(α=0.05)Tab.1 Power of the three kinds of test methods for eight models under different sample size (α= 0.05)

