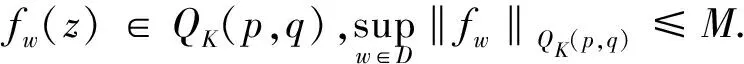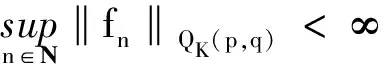QK(p,q)空间到Bloch型空间上的Stevi-Sharma算子
朱克超,赵姣珍
贵州民族大学人文科技学院, 贵州 贵阳 550025
设D是复平面上的单位圆盘,H(D)表示D上的解析函数的全体.Bloch型Bα(α>0)定义为
见文献[4].在模‖f‖Bα=|f(0)|+‖f‖α下,Bα是巴拿赫空间当α=1,Bα=B1=B是我们熟知的Bloch空间,满足

设μ是区间[0,1)上的正连续函数,且具有如下的性质:存在正数s和t(0 则称μ为正规函数[5]. Bμ空间[6~8]定义如下 在模‖f‖Bμ下,空间Bμ为巴拿赫空间[6]. Bμ的子空间记为Bμ,0,定义如下 我们称之为小Bloch空间.当μ(r)=(1-r2)α,Bμ变成Bloch型空间Bα. 在本文中,我们假定K是[0,∞)上的右连续 非负不减函数.对于0 成立时QK(p,q)=B(q+2)/p成立,并且有‖f‖B(q+2)/p≤C‖f‖QK(p,q)(文献[9]的定理2.1). 本文中总是假定 否则QK(p,q)仅由常值函数构成[9]. 令ψ∈H(D),φ是D上的解析自映射,H(D)上的复合算子,乘积算子和微分算子分别定义如下 (Cφf)(z)=(f∘φ)(z)=f(φ(z))z∈D 对于ψ1(z),ψ2(z)∈H(D)和D上的解析自映射φ,令 Tψ1,ψ2,φf(z)=ψ1(z)f(φ(z))+ψ2(z)f′(φ(z)) MψCφD=T0,ψ,φMψDCφ=T0,ψφ′,φCφMψD=T0,ψ∘φ,φ 上述六种算子的研究见文献[1]. 受上述结果的鼓励和启发,本文旨在讨论QK(p,q)空间到Bloch型空间的算子Tψ1,ψ2,φ,并分别给出Tψ1,ψ2,φ是有界算子和紧算子的充分必要条件.本文的结果是早期一些结果的推广,比如文献[2,3]. 本文组织如下:第二节给出证明主要结论需要用到的一些引理. 第三节给出主要结论并证明之. 引理2[4]令α>0且f∈Bα.那么 引理3[4]令α>0和f∈Bα.那么有 这一节我们证明主要结果. 定理1 令ψ1(z),ψ2(z)∈H(D)且φ是D上的解析自映射.μ是正规函数p>0,q>-2,q+2≠p且K是[0,∞)上的非负不减函数使得下式成立 (1) 证明 假设(a),(b),(c)成立.那么对于ψ1(z),ψ2(z)∈H(D)和f∈QK(p,q), 由‖f‖B(q+2/p)≤C‖f‖QK(p,q)及引理2和引理3,计算可知 μ(|z|)| (Tψ1,ψ2,φf)′| f′(φ(z))|+μ(|z|)|ψ2(z)φ′(z)f″(φ(z))| ≤C(M1+M2+M3)‖f‖B(q+2)/p≤C(M1+M2+M3)‖f‖QK(p,q) ‖Tψ1,ψ2,φf‖Bμ≤C‖f‖QK(p,q) (2) (3) (4) 由(2)式,(3)式和(4)式及函数φ(z)的有界性,可得 (5) 和 (6) 对w∈D,令 fw(z)=Hw,0(z)-2Hw,1(z)+Hw,2(z) 直接计算可得 对所有w∈D成立.即 ≤‖Tψ1,ψ2,φfw‖βμ≤∞ (7) 因此我们有 即 (8) (9) 由不等式(6)可得 (10) 不等式 (9) 和 (10)意味着 (11) 对w∈D,分别取测试函数 和 类似于(11)式的证明,可分别证明 和 成立.由此(a)、(b)、(c)成立,则定理1的证明完成. (12) 和 记K={z∈D:|φ(z)|≤η} 直接计算可得 ‖Tψ1,ψ2,φfn‖Bμ (13) 对于n∈N,取测试函数 (14) 另一方面, 由 (7)式和 (14)式我们有 这就意味着 进而有 即 (15) 分别取测试函数 和 用类似于(15)式证明方法,我们可以证明 成立.我们略去详细的证明过程. 定理2的证明完成.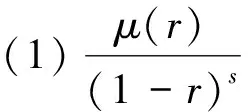
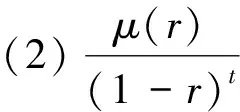

(Mψf)(z)=ψ(z)f(z)z∈D
Df(z)=f′(z)z∈D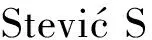
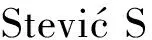
DMψCφ=Tψ′,ψφ,φCφDMψ=Tψ′∘φ,ψφ,φDCφMψ=Tψ′∘φφ′,(ψ∘φ)φ′,φ
1 辅助结果


2 主要结果的证明