量子矩阵空间Mq(2)及量子群slq(2)的坐标代数的Gröbner-Shirshov基
木娜依木·迪里夏提
新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046
0 前言
量子群的引入是 20 世纪末数学的重大成果之一. 量子群首先是在 Faddeev 为了解可积模型而研究的可逆扩散方法中出现的[1,2],而量子群slq(2) 最早是在Kulish和Reshetikhin 研究具有最高旋量的可积 XYZ模型的文献[3]中出现的.他的 Hopf 代数结构是后来被 Sklyanin 发现的[4]. 但是最主要的成果是 1985 年由Drinfeld 及Jimbo 发现的一类 Hopf 代数[5,6],这些 Hopf 代数可以被认为是复半单李代数的泛包络代数的单参变量退化,并且现在被称为 Drinfeld-Jimbo 量子群.量子群被引入后在数学和物理学的很多分支学科中得到了广泛的应用,比如在数学中的李群、李代数及其表示、特殊函数理论、钮结理论、低维拓扑学、算子代数、非交换集合及组合学等,在物理学中的量子可逆扩散方法、可积模型理论初等粒子物理及量子场论等.
为了在交换代数中解决约化问题 Buchberger 在文献[7]中引入了 Gröbner 基理论,在李代数上相应的理论是 Shirshov 在文献[8]中建立的,后来 Bergman 在文献[9] 中把 Buchberger 的理论推广到了结合代数上.接着 Bokut 发现 Shirshov 的方法对于结合代数同样有效[10].因此,现在我们把他们建立的理论统称为 Gröbner-Shirshov基理论.同样,Gröbner-Shirshov 基理论被建立后在数学的各个领域得到了广泛的应用[11].
关于量子群的 Gröbner-Shirshov 基理论的第一个文献是 Bokut 和 Malcolmson 的文献[12].在此文中作者建立了 Drinfeld-Jimbo 量子群的Gröbner-Shirshov基理论,并且具体构造了An型量子群的Gröbner-Shirshov基.后来在这方面有了很多工作[13~15].在本文我们要给出量子矩阵空间Mq(2)及量子群slq(2)的坐标代数O(Mq(2))及O(slq(2))的Gröbner-Shirshov基.
1 预备知识
这一节,我们回忆一下关于Gröbner-Shirshov 基及括号代数的一些概念.
我们设X={xi|i∈I} 是字母的一个非空集合,并且用X*表示由字母集合X中元素生成的结合词(word)的集合.我们假设X*包含空词 1.对每一个词w∈X*,我们把w所包含的字母个数称为词w的长度,并记为|w|.当然,空词1的长度为零.
设k是一个域,我们用k〈X〉表示以X*为基的k-代数, 其中两个词的乘积定义为他们的毗连(concatenation)词.为了对k〈X〉中的元素定义其首项,我们首先在X上定义一个良序 >如下:xi>xj当且仅当i>j.然后,在X*上定义一个序如下:对任意w1,w2∈X*,定义w2w2⟺|w2|<|w1|或者|w2|=|w1|且按词典排序法有w2w1.显然此序是个全序,并且被称为 deg-lex 序.半群X*上的全序自然地在代数k〈X〉上诱导出一个全序,此序我们仍然用来表示.对任意f∈k〈X〉,我们用表示多项式f的首项(对于全序).如果首项的系数为1,则多项式f称为首一多项式.
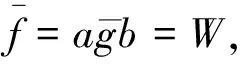
设S⊆k〈X〉是由一些首一多项式组成的集合.对于f,g∈S,如果有
其中,αi∈k,ai,bi∈X*,si∈S,则我们说合成对于(S,w)平凡,并且记为
(f,g)w≡0 mod (S,w)
如果对任意f,g∈S,都有(f,g)w≡0 mod (S,w) ,则我们说S对合成封闭.一个首一多项式的非空集合S如果对合成封闭,那么S称为k〈X〉中的一个Gröbner-Shirshov基.显然从定义可知(f,g)W∈〈S〉,其中〈S〉是由S生成的理想.因此在商代数k〈X〉/ 〈S〉中有等式(f,g)W=0.

下面的钻石合成引理是 Gröbner-Shirshov 基理论的核心结果.
引理1(钻石合成引理) 设S⊆k〈X〉是由一些首一多项式组成的非空集合,是上面定义的 deg-lex序,则下列三条等价:
(1)S是k〈X〉中的Gröbner-Shirshov基;


2 量子矩阵空间Mq(2)及量子群slq(2)的坐标代数的 Gröbner-Shirshov 基
在这一节里我们要给出量子矩阵空间Mq(2)及量子群slq(2)的坐标代数的Gröbner-Shirshov基.
2.1 量子矩阵空间Mq(2)的坐标代数的Gröbner-Shirshov基
设C是复数域,q是一个非零复数,根据文献[16],量子矩阵空间Mq(2)的坐标代数O(Mq(2))是由a,b,c,d生成的,并且满足以下关系的C-代数:
ab=qbaac=qcabd=qdbcd=qdcbc=cbad=bd+(q-q-1)bc
令X={a,b,c,d},并且在X上定义序>如下:a>b>c>d, 那么此序在由X生成的半群X*上诱导出deg-lex序≻.
我们令S1={f1,f2,f3,f4,f5,f6}, 其中
f1=ab-qbaf2=ac-qcaf3=bd-qdbf4=cd-qdcf5=bc-cdf6=ad-da-(q-q-1)bc
这时对于序≻, 我们有
由于S1中元素的首项都是二次,因此在S1中元素之间只有4个交叉合成.下面我们计算这些合成.
(1)合成(f1,f3)ω,其中ω=abd. 因此有
(f1,f3)ω=(ab-qba,bd-qdb)abd
=(ab-qba)d-a(bd-qdb)=qadb-qbad
≡q(da+(q-q-1)bc)b-qb(da+(q-q-1)bc)
≡qdab+q(q-q-1)bcb-qbda-q(q-q-1)bbc
≡qdab+q(q-q-1)bcb-qbda-q(q-q-1)bcb
≡qdab-qbdamod(S1;ω)≡q2dba-q2dba≡0 mod (S1;ω)
(2)合成(f1,f5)ω其中ω=abc因此有
(f1,f5)ω=(ab-qba,bd-cb)abc
=(ab-qba)c-a(bc-cb)=acb-qbac
≡qcab-q2bca
≡q2cba-q2cba≡0 mod (S1;ω)
(3)合成(f2,f4)ω其中ω=acd,因此有
(f2,f4)ω=(ac-qca,cd-qdc)acd
=(ac-qca)d-a(cd-qdc)=qadc-qcad
≡q(da+(q-q-1)bc)c-qc(da+(q-q-1)bc)
≡qdac+q(q-q-1)bcc-qcda-qc(q-q-1)bc
≡qdac+q(q-q-1)cbc-q(q-q-1)cbc-qcda
≡qdac-qcda≡q2dca-q2dca≡0 mod (S1;ω)
(4)合成(f5,f4)ω其中ω=bcd.因此有
(f5,f4)ω=(bc-cb,cd-qdc)bcd
=(bc-cb)d-b(cd-qdc)=qbdc-cbd
≡qbdc-cqdb≡q2dbc-qcdb≡q2dbc-q2dcb
≡q2dcb-q2dcb≡0 mod (S1;ω)
所以我们得到
定理1 集合S1是量子矩阵空间Mq(2)的坐标代数O(Mq(2))的一个Gröbner-Shirshov 基.
由引理1,我们有
推论1 Irr(S)={u∈〈X〉|u=dl1cl2bl3al4,li≥0,i=1,2,3,4}是坐标代数O(Mq(2))/〈S〉的一个线性基.
2.2 量子群slq(2)的坐标代数O(slq(2))的Gröbner-Shirshov基
设C是复数域,q是一个非零复数,根据文献[16],量子群slq(2)的坐标代数O(slq(2))是由a,b,c,d生成的,并且满足以下关系的C-代数:
ab=qbaac=qcabd=qdbcd=qdcbc=cbad-qbc=da-q-1bc=1
令X={a,b,c,d},并且在X上定义序>如下:a>b>c>d,那么此序在由X生成的半群X*上诱导出deg-lex序≻.我们令S2={f1,f2,f3,f4,f5,f6,f7,f8} 其中
f1=ab-qbaf2=ac-qcaf3=bd-qdbf4=cd-qdc
f5=bc-cbf6=ad-qbc-da+q-1bcf7=ad-qbc-1
f8=bc-qda+q
这时对于序≻,我们有
由于S2中元素的首项都是二次,因此在S2中元素之间只有 6 个交叉合成.下面我们计算这些合成.
(1)合成(f1,f3)ω,其中ω=abd. 因此有
(f1,f3)ω=(ab-qba,bd-qdb)abd
=(ab-qba)d-a(bd-qdb)
=qadb-qbad
≡q(qbc+1)b-qb(qbc+1)
≡q2bcb+qb-q2bbc-qb
≡q2bcb-q2bcb
≡0 mod (S2;ω)
(2)合成(f1,f5)ω,其中ω=abc.因此有
(f1,f5)ω=(ab-qba,bc-cb)abc
=(ab-qba)c-a(bc-cb)
=qcab-qbac
≡q2cba-q2bca
≡q2cba-q2cba
≡0 mod (S2;ω)
(3)合成(f1,f8)ω,其中ω=abc.因此有
(f1,f8)ω=(ab-qba,bc-qda+q)abc
=(ab-qba)c-a(bc-qda+q)
=qada-qbac-qa
≡q(qbc+1)a-qbac-qa
≡q2bca+qa-qbac-qa
≡q2bca-q2bca
≡0 mod (S2;ω)
(4)合成(f2,f4)ω,其中ω=acd.因此有
(f2,f4)ω=(ac-qca,cd-qdc)acd
=(ac-qca)d-a(cd-qdc)
=qadc-qcad
≡q(qbc+1)c-qc(qbc+1)
≡q2bcc+qc-q2cbc-qc
≡q2cbc-q2cbc
≡0 mod (S2;ω)
(5)合成(f5,f4)ω,其中ω=bcd.因此有
(f5,f4)ω=(bc-cb,cd-qdc)bcd
=(bc-cb)d-b(cd-qdc)
=qbdc-cbd
≡q2dbc-cqdb
≡q2dbc-q2dcb
≡q2dcb-q2dcb
≡0 mod (S2;ω)
(6)合成(f8,f4)ω,其中ω=bcd.因此有
(f8,f4)ω=(bc-qda+q,cd-qdc)bcd
=(bc-qda+q)d-b(cd-qdc)
≡qbdc-qdad+qd
≡qbdc-qd(qbc+1)+qd
≡qbdc-q2dbc-qd+qd
≡q2dbc-q2dbc
≡0 mod (S2;ω)
所以我们得到
定理2 集合S2是量子群Mq(2)的坐标代数O(Mq(2))的Gröbner-Shirshov基.
由引理1我们有
推论2 Irr(S)={u∈〈X〉|u=dl1cl2bl3al4,li≥0,i=1,2,3,4}是坐标代数O(slq(2))/〈S〉的一个线性基.

