中间约束轴向运动梁横向非线性振动

赵小颖, 李 彪, 丁 虎, 陈立群,3

(1. 上海大学 上海市应用数学和力学研究所, 上海 200072;2. 上海卫星工程研究, 上海 200240; 3. 上海大学 力学系, 上海 200444)

作为航天工程、机械生产、日常生活中常见的沿着轴向移动的柔性连续体体的力学模型，自20世纪60年代Mote院士提出动力学模型[1]以来，轴向运动梁已经得到广泛的研究。基于不同工况下的轴向运动梁，横向自由振动频率得到了研究[2-5]。也有研究人员关注于受到外部激励的轴向运动梁的振动特征研究[6-8]。Marynowski等[11]综述了2014年以前轴向运动弹性振动相关的研究进展。

有很多工况需要在轴向运动梁中部添加弹性支撑或者约束，例如，空中缆车的缆绳，为了增加刚度，会增加支撑；再如，为了抑制轴向运动系统的横向振动，会在系统中间弹性吸振装置，等等。尽管对于包含中间弹性约束的柔性体已经得到广泛的研究[10-13]，但是对于中间弹性约束影响轴向运动系统动力学特征的研究并不多见。Ghayesh[14]研究了中间黏弹性约束对轴向运动弦线的非线性振动特性的影响，包括周期响应与分岔混沌特征。Zhang等[15]研究了轴向运动梁在初始激励作用下，非线性吸振器对系统的暂态振动的吸收效果，证明非线性吸振器的优异吸振效果。需要说明的是，以上提到的文献都是基于Galerkin截断方法的研究结果，对于中间约束的轴向移动柔性体，移动速度对约束的作用效果的影响、截断阶数的收敛性都没有做出说明。目前，还缺乏对轴向运动速度和中间弹性支撑或者约束相互影响的研究。

本文运用Galerkin截断方法研究了在两端简支边界条件下，中间弹簧刚度、轴向运动速度、不同截断阶数对轴向运动梁固有振动频率的影响，并通过对比，给出了收敛的假设模态截断阶数。另外，本文还研究了中间弹簧刚度、轴向运动速度对稳态响应的影响。数值结果表明，中间弹性约束对轴向移动梁振动有着复杂影响，沿着轴向运动的速度会增加中间约束对梁自由振动频率和受迫振动响应影响的复杂性。

1 数学模型和控制方程

图1所示为带有中点约束的轴向运动梁力学模型，在距离梁左边界xs处加上了弹簧支撑，刚度系数为k。其中ρ为轴向运动梁的质量密度，A为横截面面积，E为弹性模量，I是关于中性轴的截面惯性矩，EI为梁的弯曲刚度，P0是梁的初始轴向张力。梁以固定速度Γ沿着其轴向运动，梁长为L。

图1 轴向运动梁物理模型

轴向运动梁的动能T和势能U的表达式分别为

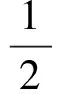
(w,t+Γw,x)2}dx

(1)

(2)

式中：w(x,t)是梁的横向位移，u(x,t)是梁的径向位移，t是时间坐标，δ(x)表示狄拉克函数，式(1)第一项为轴向运动梁与纵向运动有关的动能，第二项为轴向运动梁与横向运动有关的动能。式(2)第一项是与轴力P0有关的势能，第二项是中性面拉伸产生的势能，第三项是与曲率有关的势能，最后一项是与中点约束弹簧有关的势能。根据Hamilton变分原理，有

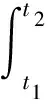
(3)

随时间简谐变化的分布力所做虚功为

(4)

由此可以得到如下控制方程

ρA(w,tt+2Γw,xt+Γ2w,xx)-

EIw,xxxx-P0w,xx+δ(x-xs)(kw)=

F(t)cos(ωt)

(5)

ρA(u,tt+2Γu,xt+Γ2u,xx)-

EA(u,xx+w,xw,xx)=0

(6)

因为纵向位移比横向位移小很多，并且EA>>ρA，所以可以得到

u,xx+w,xw,xx=0

(7)

由上式可以得到

(8)

其中，C1(t)和C2(t)是关于时间t的函数。

两端简支边界纵向边界条件为

u(0,t)=0,u(L,t)=0

(9)

将式(8)代入式(9)得到

(10)

将式(10)代入式(5)得到

ρA(w,tt+2Γw,xt+Γ2w,xx)+

EIw,xxxx-P0w,xx+kwδ(x-xs)-

(11)

两端简支边界横向边界条件为

w(0,t)=w(L,t)=0,

w,xx(0,t)=w,xx(L,t)=0

(12)

通过无量纲化得到控制方程

w,tt+2γw,xt+(γ2-1)w,xx+kwδ(x-xs)+

F(t)cos(ωt)

(13)

无量纲参数定义如下

(14)

无量纲简支边界条件为

w(0,t)=w(1,t)=0,

w,xx(1,t)=w,xx(0,t)=0

(15)

2 Galerkin截断

设式(13)的解为

j=1,2,…,M

(16)

将(16)式代入控制方程后得到

(17)

假定，上面等式等号左边的式子等于RM(x,t)，式RM(x,t)应满足

i=1,2,…,M

(18)

即可实现对控制方程的M阶Galerkin截断，最终将方程转化为含有M个未知数为qj(j=1,2,…,M)的常微分方程组。将中间弹簧设置在xs=L/2处。

计算自由振动频率时，忽略上式中的非线性，通过无量纲化得到控制方程

w,tt+2γw,xt+(γ2-1)w,xx+

(19)

对于给定的轴向速度、中间刚度系数和截断阶数，通过广义本征值问题，即可求得前M阶固有频率。

3 固有频率

下面取8阶Galerkin截断(M=8)。取梁的长度L=0.3 m,杨氏模量E=200 MPa，初始张力P0=80 N，ρ=1 200 kg/m3，梯形截面上底宽0.022 m，下底宽0.008 9 m，高度0.018 m，kf=0.442 8。图2给出了前两阶固有频率随速度变化曲线。从上图可以看出，前两阶固有频率随着中间弹簧刚度的增加不断增大，图2(a)中清楚的显示当无量纲约束刚度超过35以后，梁的轴向临界速度不再变化。图2(b)表明，当轴向运动速度为零时，第二阶固有频率不受中点约束的影响。但是随着速度的增大，约束刚度对第二阶固有频率的影响变得越发显著。更加有趣的是，当无量纲约束刚度取值大于200时，在运动速度不大时，第二阶固有频率会随速度增大而增大。

图3给出了速度对不同刚度下轴向运动梁前两阶横向振动固有频率的影响。从图(a)和(b)中可以看出，当轴向运动速度为零时，第二阶固有频率开始不随中点约束刚度变化，而第一阶频率持续增大。但是当无量纲约束刚度增大到220左右时，第一阶频率超过第二阶频率。最初的第二阶模态对应的频率成为最小的频率，即基频，最初的第一阶模态对应的频率不再是最小的频率，成为第二阶频率，继续增大。这一前两阶频率转换的现象同样发生在轴向运动速度不为零的工况。另外，还需要说明的是，轴向运动的速度会使得中间弹簧无量纲刚度系数小于200时梁的第二阶固有频率受到中点约束弹簧的影响。如图所示，速度为零时，此时的第二阶固有频率不随中间约束刚度变化。因此可以判定，轴向移动的速度使得原本中点对称的模态，不再对称。

图4比较了不同截断阶数对前两阶固有频率的影响。截断阶数分别取M=4、8、16和24阶，中间弹簧无量纲刚度系数k取200。对于前2阶固有频率的预测，4种截断阶数给出了相同的变化趋势。8、16和24阶截断对应的第一阶固有频率基本重合。相比之下，4截断的结果与8、16、24阶截断结果的差别随固有频率的阶数增大而增大，第一阶和第二阶固有频率间，有可识别的差别。

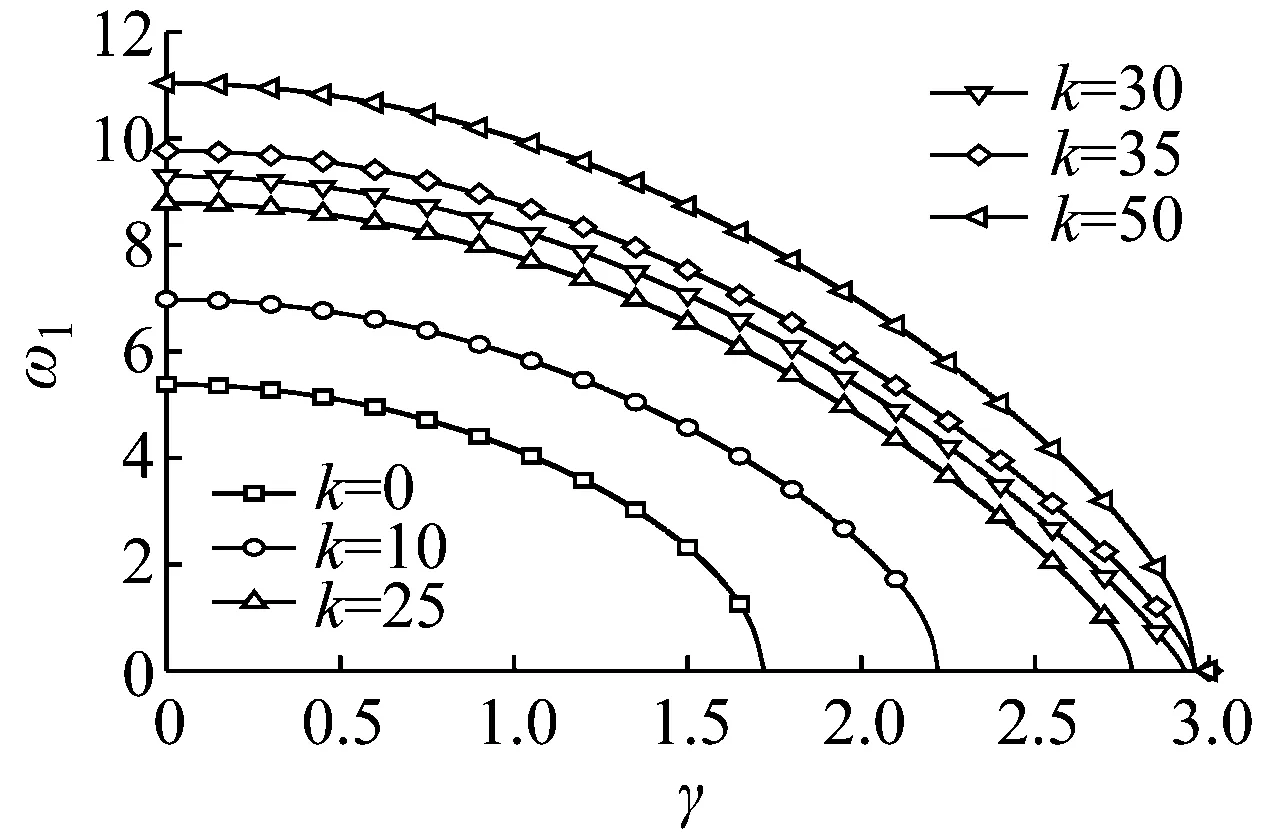
(a) 第一阶固有频率

(b) 第二阶固有频率

(a) 第一阶固有频率

(b) 第二阶固有频率

(a) 第一阶固有频率

(b) 第二阶固有频率

4 稳态响应

取无量纲阻尼系数μ=1.161 3，无量纲外激励F=0.3，其他参数与图2一致。

图5(a)为轴向运动梁在距离左端1/4点处的稳态响应曲线。通过观察发现，速度的变化对曲线有着明显的影响。既改变轴向运动梁横向受迫振动的共振区，也改变梁的共振幅度。图5(b)通过改变中间弹簧约束的刚度值发现，在一定范围内，随着刚度k的增加，轴向运动梁前两阶共振逐渐接近。另外，轴向运动速度的增大和中间约束的减小，梁的振动幅度都会增大，而且非线性跳跃的区域也都会随着增大。

(a) 稳态响应(k=100)

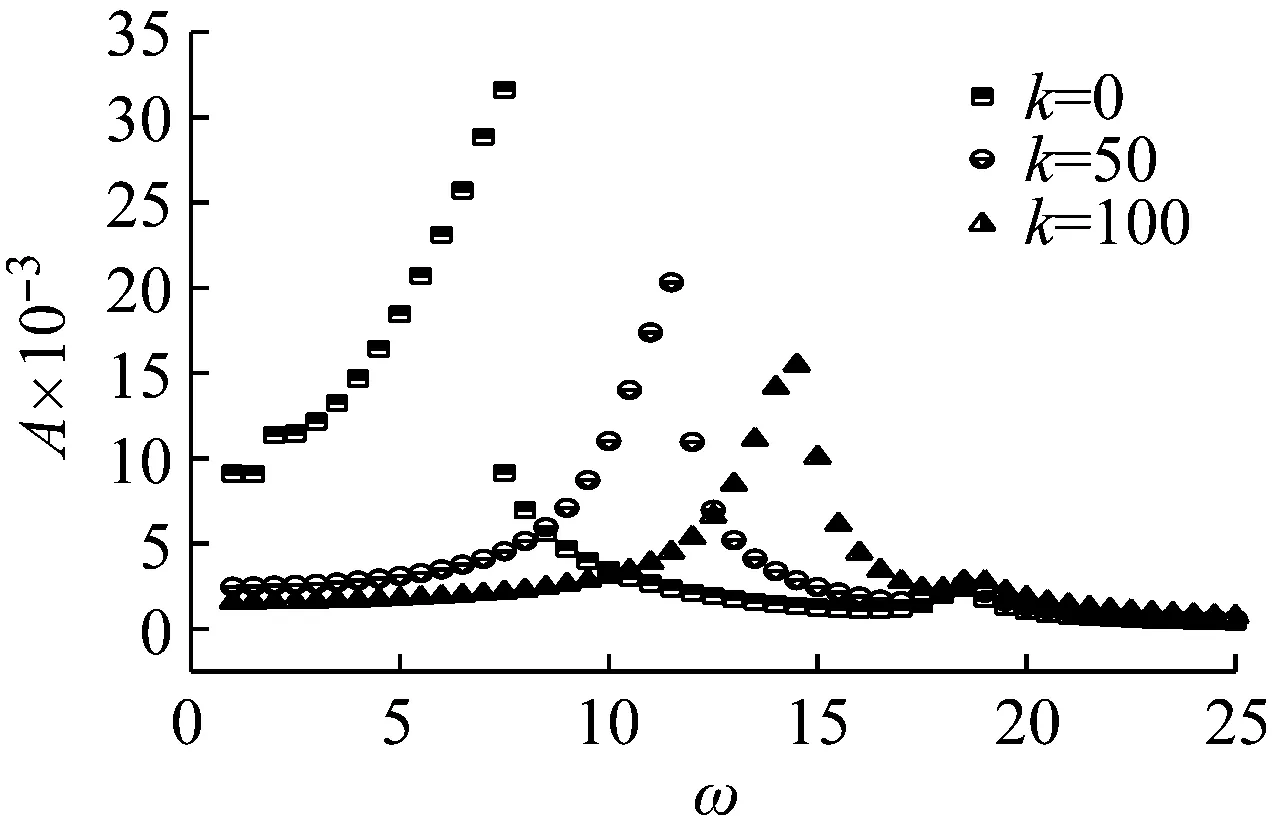
(b) 稳态响应(γ=0.5)

5 结 论

本文运用Galerkin截断方法，研究了带有中间约束的轴向运动梁的横向非线性振动。得到了不同中间约束刚度系数下，轴向运动速度与频率的变化关系曲线以及稳态响应曲线，分析了不同变化因素对固有频率及稳态响应曲线的影响以及研究方法的收敛性。研究揭示了中间弹性约束和轴向运动速度的共同作用对梁固有频率及稳态响应的复杂影响。发现中间约束刚度的增加会导致轴向运动梁的固有频率不同程度的增加，尽管中间约束对静态梁偶数阶模态无影响。更有意思的是，约束刚度的增加会使得前两阶模态的频率相互转换。另外，还发现4阶Galerkin截断的计算结果与高阶截断相比较，存在可以辨识的误差。而在横向非线性受迫振动方面发现，轴向运动速度和中间弹性约束刚度的影响会有叠加效应，两个因素的共同作用下，梁的稳态响应会产生复杂的变化趋势。