基于F-CNN的雷达目标辨识算法

， ， ，

(1.国防科技大学电子对抗学院， 安徽合肥 230031；2.空军研究院战略预警研究所， 北京 100089)

0 引 言

近年来，随着电子战的重要性日益凸显，敌我双方对电磁频谱的争夺逐渐加剧，雷达干扰技术迅速发展且相关新兴技术被广泛应用[1]。同时，雷达抗干扰技术也获得相应的发展。但是，这些抗干扰措施[2-4]更多依赖人工判断和设定，缺乏客观性和精确性，这也成为制约雷达抗干扰技术发展的关键因素之一[5]。

近些年，深度学习算法研究发展迅速，将相关算法应用到电子战中正逐渐成为雷达抗干扰研究的新趋势[6]。姚毅等将卷积神经网络(Convolu-tional Neural Network, CNN)运用到雷达反欺骗干扰领域[7]，不依赖设计者的经验，采用数据训练，取得了98.83%的识别率。但是，姚毅等搭建的卷积神经网络存在识别参数庞大的问题，不利于实时处理。

本文提出了一种基于分解卷积神经网络(Factorized Convolutional Neural Network, F-CNN)的雷达目标辨识算法。以深度可分离卷积[7](Depthwise Separable Convolution, DSC)结构为基础搭建分解卷积神经网络，以及对分解卷积神经网络进行精简[8]，使用实测数据对两个网络模型进行训练和测试，并对结果进行分析讨论。

1 分解卷积神经网络的模型结构

本节详细介绍具体的卷积结构(深度可分离卷积结构)及网络模型(分解卷积神经网络模型)。

1.1 深度可分离卷积的结构

假设输入图像矩阵I∈h×w×m，其中h表示图像的高，w表示图像的宽，m表示图像通道数；卷积核矩阵K∈k×k×m×n，其中k表示卷积核尺寸，n表示卷积核数。在标准卷积运算中，取步长为1，且对边界不进行补零操作时，输出图像矩阵为O∈(h-k+1)×(w-k+1)×n。计算公式[7]为

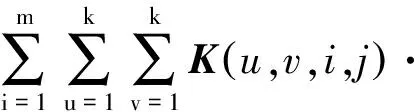
I(y+u-1,x+v-1,i)

1≤y≤h-k+1,1≤x≤w-k+1,1≤j≤n

(1)

式中，O(y,x,j)表示标准卷积输出图像矩阵O的第(y,x,j)个元素。式(1)其他矩阵类似O(y,x,j)表述的含义与其含义相似。

式(1)的计算量为

C1=k2mnhw

(2)

标准卷积的卷积核模型如图1所示。

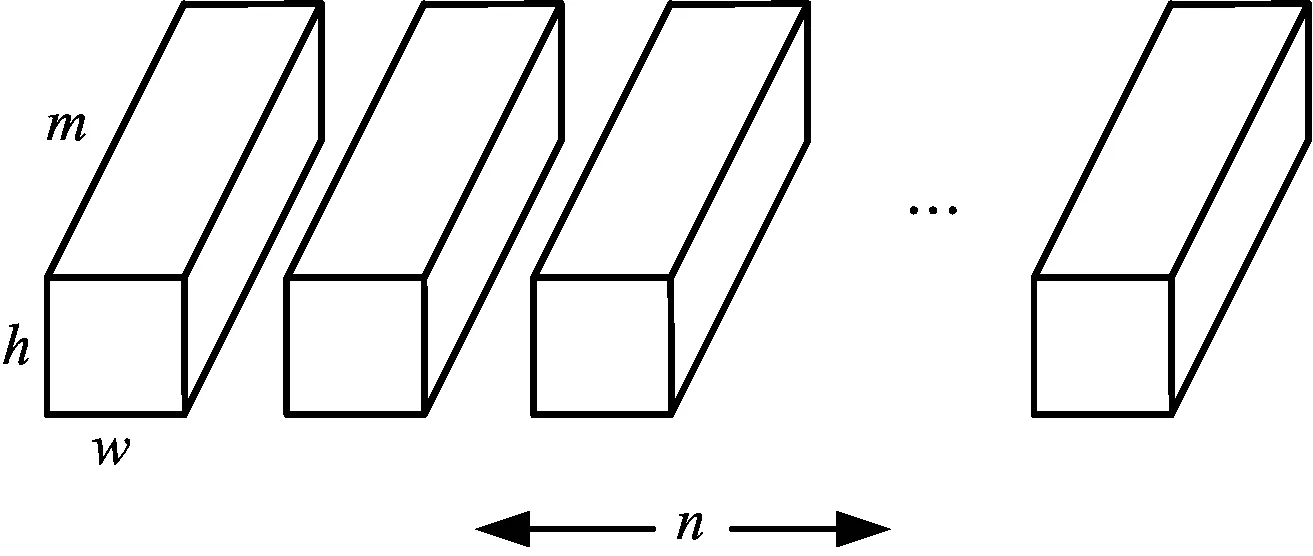
图1 标准卷积核

深度可分离卷积是将标准卷积运算分解为逐通道卷积(Depthwise Convolution，DC)和逐点卷积(Pointwise Convolution，PC)。逐通道卷积过滤输入图像，提取特征。逐点卷积则是将提取的特征进行加权合并。

逐通道卷积的卷积核和逐点卷积的卷积核模型分别如图2和图3所示。

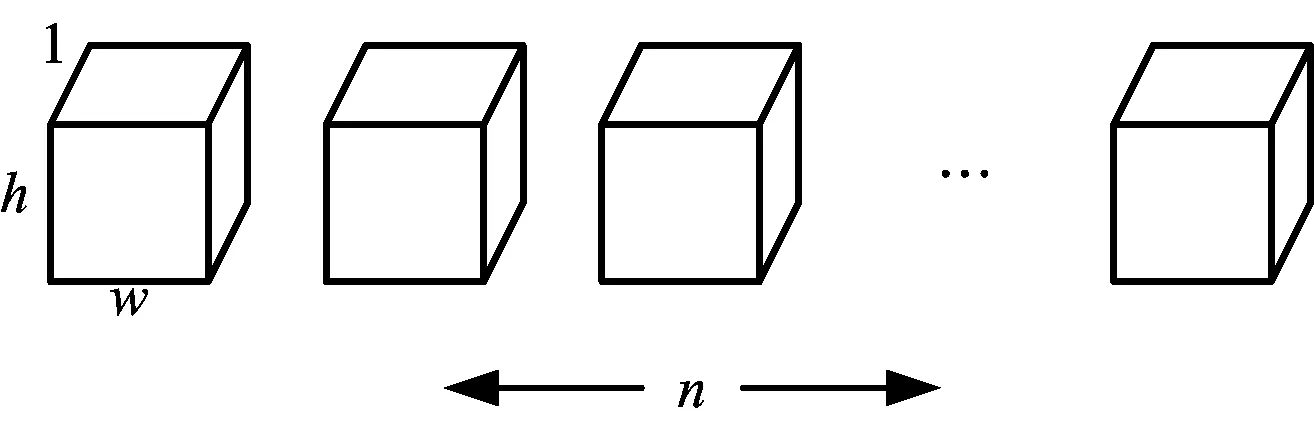
图2 逐通道卷积核

图3 逐点卷积核

给定输入图像矩阵，逐通道卷积核P∈k×k×1×m，逐点卷积核Q∈1×1×m×n。在卷积运算步长为1，且对边界不进行补零操作时，通过分解卷积运算，可以得到输出图像矩阵。计算过程如下：

逐通道卷积公式[7]为

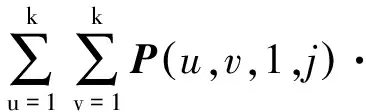
I(y+u-1,x+v-1,j)

1≤m≤h-k+1, 1≤n≤w-k+1, 1≤j≤m

(3)

式中，G(m,n,j)表示逐通道卷积后输出矩阵G中的第(m,n,j)个元素。式(3)其他矩阵类似G(m,n,j)表述的含义与其含义相似。

逐点卷积公式[7]为

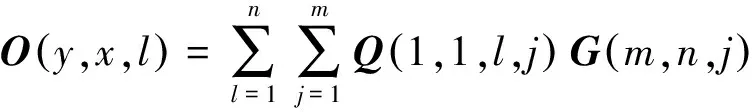
1≤y≤h-k+1, 1≤x≤w-k+1, 1≤l≤n

(4)

式(4)其他矩阵类似G(m,n,j)表述的含义与其含义相似。

深度可分离卷积的计算量为

C2=k2mhw+mnhw

(5)

深度可分离卷积的计算量与标准卷积的计算量之比，可以得到如下结果：

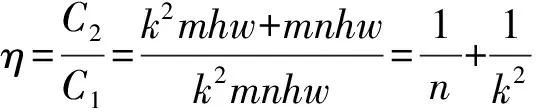
(6)

式中，当k=5，n=32时，η≈7%，即相同情况下深度可分离卷积运算的计算量仅有标准卷积运算的7%。

1.2 模型搭建与训练

参照卷积神经网络的经典模型LeNet-5[9]，并比照卷积神经网络模型[7]，搭建分解卷积神经网络。其网络框图如图4所示。

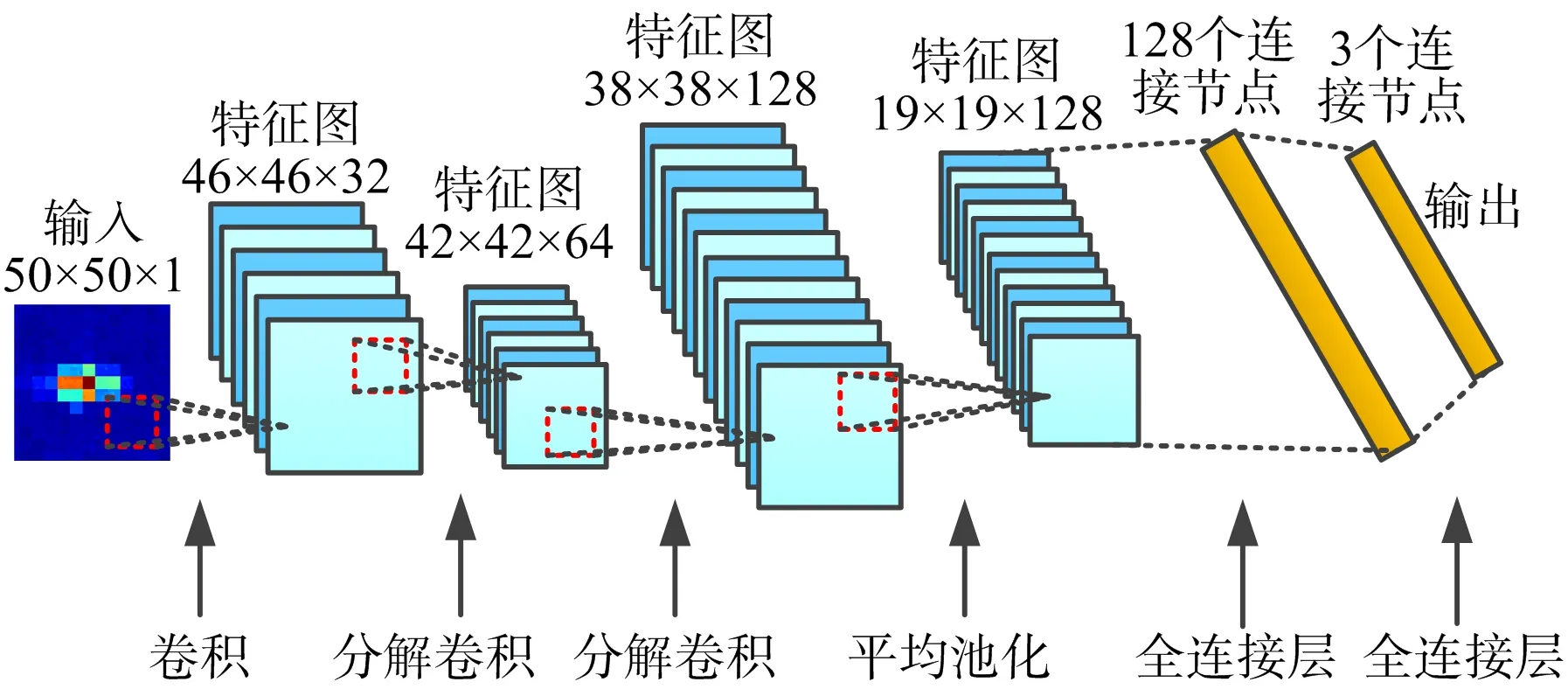
图4 分解卷积神经网络框图

分解卷积神经网络由1个输入层、3个卷积层(1个标准卷积和2个分解卷积)、1个池化层、2个全连接层、1个输出层组成。实际运算中，为了及时有效地调整数据，需要引入块归一化(Batch Normalization)操作[10]、激活(Activation)操作[11]、平整(Flatten)操作、弃离(Dropout)操作。块归一化操作可使输出服从均值为0、方差为1的标准正态分布。引入激活函数可以添加输出的非线性因素。平整操作则是将矩阵拉伸成向量，便于全连接层进行特征提取。弃离操作是为了有效减少过拟合的情况。

各个层级输出样本大小和参数数量如表1所示。

表1 分解卷积神经网络输出样本大小和参数数量统计

注：输出大小中的“None”表示不限制输出和输入的数量。

分解卷积神经网络模型中，6个层级共使用了5 929 283个参数，是卷积神经网络参数数量的近3倍。同时全连接层参数数目占总参数数目的99.75%。

参数数量过多将会严重影响识别的速率，为此对该网络模型进行精简，搭建精简分解卷积神经网络。在原网络层数不变的前提下减少卷积核数和第一个全连接层连接节点数。精简分解卷积神经网络框图如图5所示。

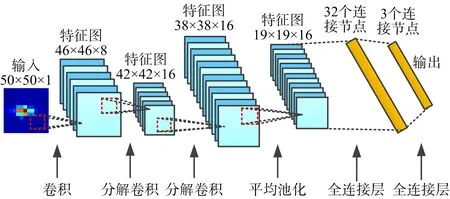
图5 精简分解卷积神经网络框图

精简分解卷积神经网络与分解卷积神经网络相比较，各个层级的参数数量均减少，而全连接层参数数量减少得最多。各个层级输出大小和参数数量统计如表2所示。

表2 精简分解卷积神经网络输出样本大小和参数数量统计

注：“None”表示对输出图片的数量并没有限制。

精简分解卷积神经网络中6个层级共使用186 371个参数，全连接层参数依旧占到了全部参数的99%以上。

2 网络模型的训练与测试

本节主要讲述用实测数据样本对两个网络模型进行训练和测试，并对测试结果进行比较分析。

实验数据均为实测数据，数据包括真实目标样本、地杂波样本、密集假目标样本。数据二维平面显示如图6所示。

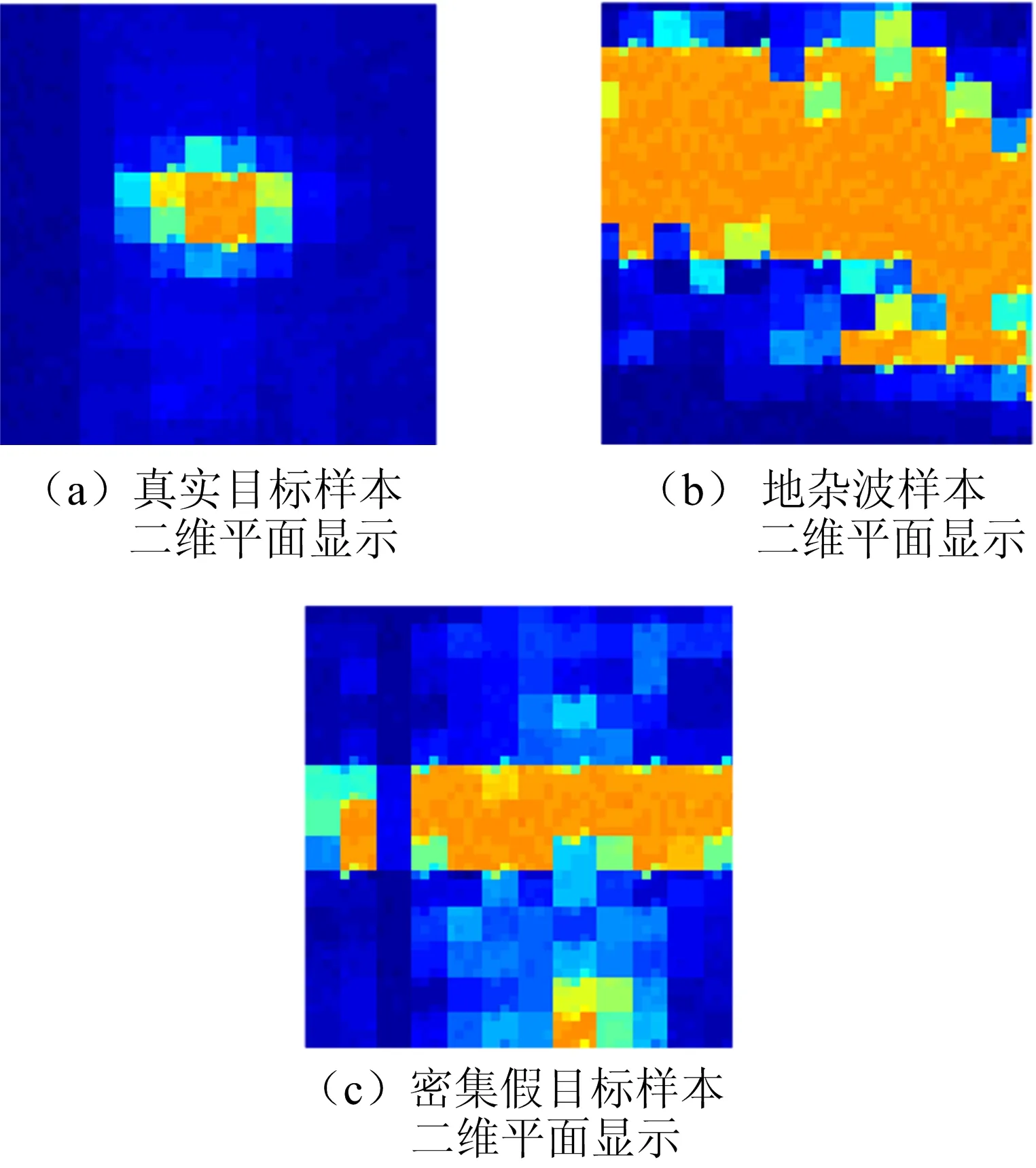
图6 某型雷达实测数据不同样本平面显示

对采集到的数据进行合理切块和数据扩充。组建相应的训练集和测试集，对搭建好的网络模型进行训练和测试。数据扩充可以弥补数据量不足的缺点，增加训练集和测试集。扩充方式如图7所示。

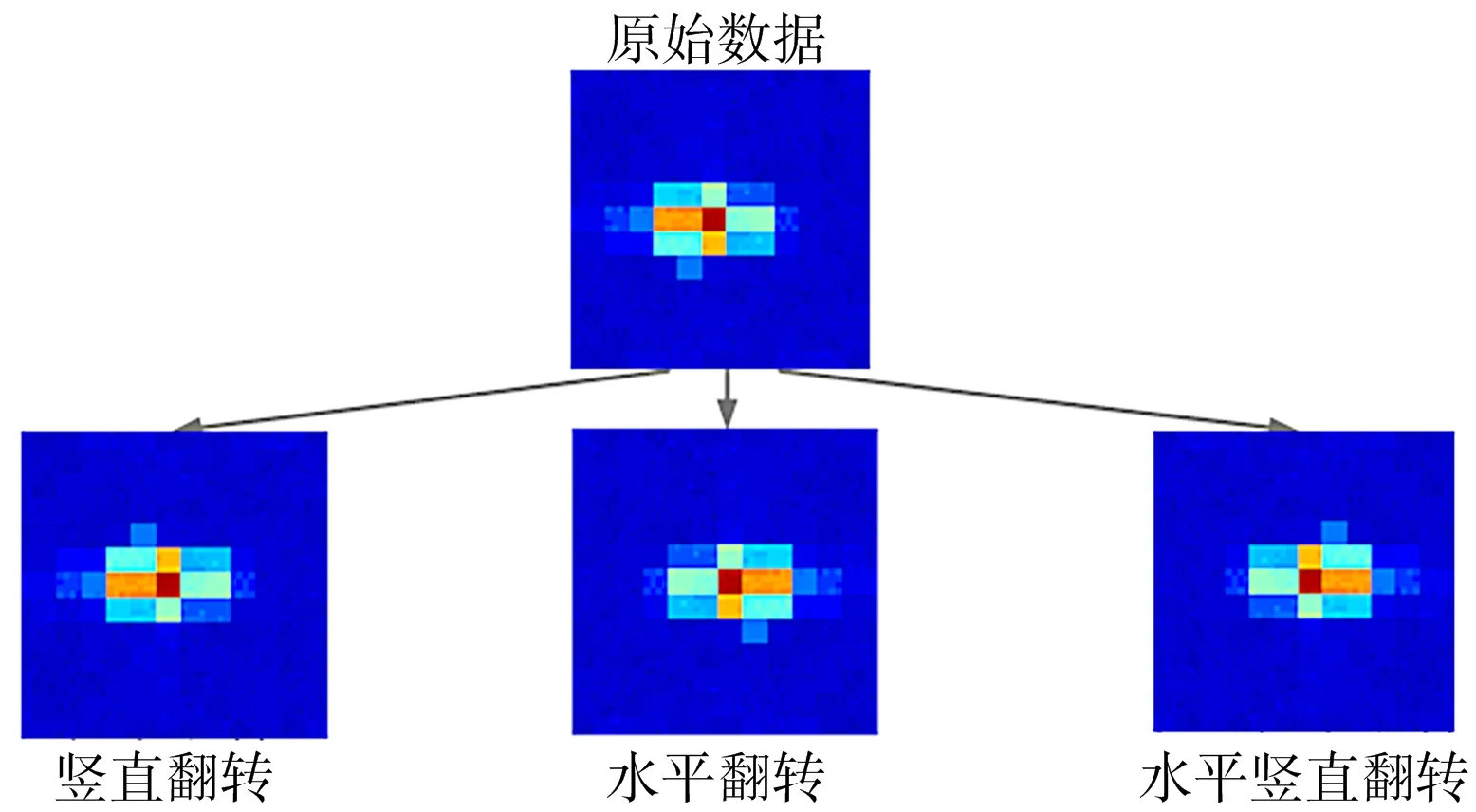
图7 数据扩充

网络模型的训练和测试均是基于Keras深度学习框架，采用Python语言编写程序。实验使用的具体硬件平台为CPU：Inter Xeon E5-2620 v3 @2.4 GHz，GPU：GTX TITAN X。

采用与卷积神经网络相同的数据对模型进行训练和测试，在每一轮迭代结束后统计识别率，可以得到如图8所示的统计结果。

图8 3种模型识别率比较

图8表明，分解卷积神经网络和精简分解卷积神经网络在经过3次迭代之后，其识别率均比卷积神经网络更高。

3种模型由于卷积结构、卷积核尺寸和全连接层连接节点不同，使得其识别率和参数数量两种性能均存在差异。对两种性能进行统计，得到表3。

表3 3种网络模型综合性能分析

表3表明分解卷积神经网络的识别率最高，但是参数数量也是最多，是卷积神经网络的近3倍。精简分解卷积神经网络识别率也较高，参数数量却仅占卷积神经网络的8.56%。

3 结束语

雷达目标辨识是雷达抗干扰的基础。本文提出了基于分解卷积神经网络的雷达目标辨识算法，实测雷达数据处理结果表明，分解卷积神经网络的识别率在卷积神经网络的基础上再提升近一个百分点，但是网络参数量庞大，不利于实时高效处理。精简分解卷积神经网络在卷积神经网络识别率的基础上提升0.4个百分点，参数数量大幅度减少，仅占卷积神经网络参数数量的8.56%。与卷积神经网络相比较，本文所提的算法对真实目标样本、地杂波样本、密集假目标样本均能提升辨识准确率。如何对真实目标进行详细区分将是下一步的研究重点。