分布式MIMO雷达的目标定位

， ，

(1.驻马店职业技术学院， 河南驻马店 463000；2.黄淮学院国际教育学院， 河南驻马店 463000)

0 引 言

近期，多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达系统得到迅速发展。由于MIMO雷达系统在检测和定位方面的优势，MIMO雷达系统也得到广泛关注。通常将MIMO雷达分为隔离(分布式)天线[1]和阵列天线[2]两类。前者充分利用空间分集，而后者是充分利用波形分集。

目前，研究人员对分布式雷达[3-4]的目标位置估计进行了大量的研究。雷达定位算法通常可划分为直接或间接两类。后者首先利用互模糊函数测量延时时间，然后再将时间与信号传播速度相乘，进而获取双基测距(Bistatic Range, BR)值，其是发射器-目标和目标-接收器的距离之和。这些BR值可形成一系列的椭圆等式，再通过这些等式估计目标位置。文献[5]提出线性无偏差估计算法，并利用泰勒序列展开算法求解非线性等式。但是，此算法的不足之处在于定位精度依赖于初始值。文献[6]提出封闭式最小二乘(Least Square, LS)算法。此外，文献[7]将目标定位问题转化为约束二次等式规划(QCQP)问题，进而对椭圆等式进行线性化，然后再利用权重LS算法(WLS)求解，最终获取目标的位置。而文献[8]提出一个分布式目标定位算法。此算法先依据不同的发射参数或接收参数将测量值划分不同的聚类，然后再在每个聚类内利用双重WLS估计算法，进而获取独立的目标位置的估计值。然后，再将不同聚类的位置估计值进行融合，形成最终的估计值。文献[9]和文献[10]分别提出基于封闭的一种WLS(OSWLS)的目标定位算法。

为此，本文先将目标定位问题转化为QCQP问题。由于QCQP的约束条件是非凸的，因此，QCQP问题为非凸、NP-hard。为了解决此问题，将每个非凸约束转化为线性约束。通过将QCQP问题转化为线性约束二次规划(LCQP)问题，再利用迭代CWLS算法求解，最终获取目标位置的解。

1 问题的描述

假定分布式的MIMO雷达系统由M个发射和N个接收天线组成。假定第i个发射器和第j个接收器的位置分别为xt,i=[xt,iyt,izt,i]T和xr,j=[xr,jyr,jzr,j]T，且i=1,…,M,j=1,…,N。发射器发射一系列正交波，由未知目标反射。目标位置表示为x0=[x0y0z0]T。然后，接收器分别收集来自发射器和目标的直接和反射信号，进而估计目标位置。

假定目标与第i个发射器的欧式距离rt,i：

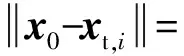
(1)

相应地，目标与第j个接收器的欧式距离rr,j：

(2)

BR定义为目标与发射器的欧式距离rt,i和目标与接收器的欧式距离rr,j之和，如式(3)所示：

ri,j=rt,i+rr,j

(3)

对式(3)两边平方，并令αi=rt,i，再经代数处理，可得

(4)

(5)

通过忽略式(5)的二次噪声项，测距误差可表示为

(6)

将式(6)转换成矩阵形式，并考虑所有发射器和接收器，便可形成

(7)

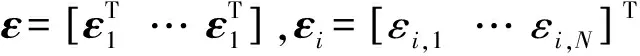
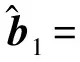
(8)

为此，可将误差矢量ε表述关于噪声变量n的函数：

ε=Bn

(9)

(10)

注意到式(7)是关于θ的线性关系。因此，可通过WLS估计算法求解未知矢量θ。可通过最小成本函数εTwε获取式(7)的WLS的解，如式(11)所示：

(11)

式中，W为对称正矩阵，其定义如式(12)所示：

W=E[εεT]-1=(BQBT)-1

(12)

式中，Q=E[nnT]-1表示噪声协方差矩阵。值得注意的是，未知位置矢量θ由未知目标位置x0和参数α组成。由于未知目标位置和参数αi，且i=1,…,M并非相互独立。因此，通过式(11)求解式(7)的解并非是式(7)的最优解。

为了提高定位精度，可将未知位置x0与参数中每个参数的关系应用于定位问题。因此，通过考虑这些关系，定位问题可表述为[7]

(13)

式(13)所示的目标定位的问题是一个非凸二次等式优化问题。

接下来用迭代的CWLS算法求解式(13)问题搜索目标的过程中，有许多随机因素的影响，所以雷达发现目标的距离也是一个随机变量。

2 迭代CWLS(ICWLS)算法

雷达的ICWLS算法先将式(13)所示的目标定位问题转化为约束二次等式规划问题(QCQP)，然后再通过对非凸约束进行转换，将QCQP问题转化为LCQP问题，最后再利用ICWLS算法求解，获取目标位置，如图1所示。

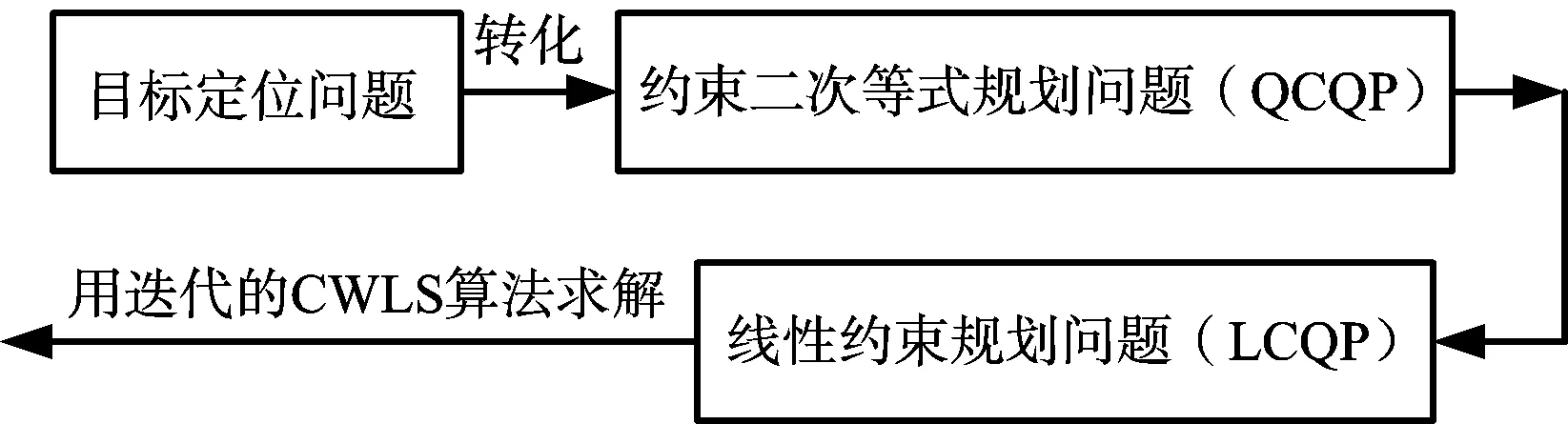
图1 目标定位问题的求解过程

2.1 QCQP问题

将式(13)的目标定位问题从非凸转化为凸式问题，如式(14)所示：

(14)

尽管式(14)的目标函数是凸的，但是二次等式约束仍是非凸的。因此，式(14)所示的目标问题属于非凸QCQP问题，其通常也是NP-hard问题。

2.2 LCQP问题

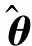
(15)

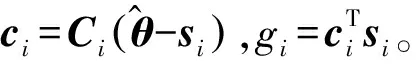
2.3 基于ICWLS求解LCQP问题的解

为了推导式(15)所示的LCQP问题的最优解，将线性约束转化矩阵形式，进而形成等式约束：

Gθ=g

(16)

式中，G=[c1…cM]T,g=[g1…gM]T。

依据矩阵的广义逆理论(Generalized Inverse Theory)，式(16)的解可表示为

(17)

式中，ξ为arbitrary矢量，P-=I-G+G为投影矩阵,而G+的定义如式(18)所示：

G+=GT(GGT)-1

(18)

将式(17)代入式(15)所示的目标函数，便可产生：

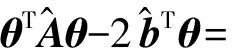
(19)

最小化关于变量θ的式(15)所示的目标函数，等于通过变量ξ最小化式(19)。因此，式(19)右边进行关于ξ的偏导数，并令其等于零，便可获取ξ的最优值：

(20)

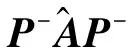
(21)

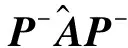
(22)

将每次迭代的最终解看成上次迭代的解与式(15)问题的解的结合，因此，对于第k次迭代，可得[11]

(23)

式中，λ为遗忘因子，且0<λ<1。λ值越大，收敛速度越快。因此，ICWLS算法通过迭代地解决定位问题，并更新解。

迭代CWLS的目标定位算法总结如下：

1) 参数初始化：

2) 设置迭代次数k=k+1，再运用近似LCQP算法：

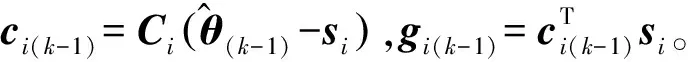
3) 再求解第2)步的解：

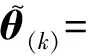
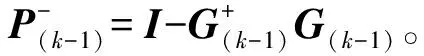
4) 获取第k次迭代的目标位置估计值：

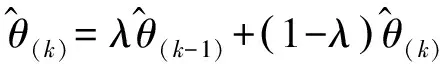
5) 检测是否满足收敛。即检测是否满足式(24)，其中δ为收敛阈值。如果满足，则终止迭代，否则进入第6)步。

(24)

3 仿真结果分析

为了更好地分析ICWLS定位算法的性能，建立Monte Carlo仿真实验。考虑文献[12]所述的MIMO雷达系统，且M=9,N=8。这9个发射器和8个接收器的参数如表1所示。

表1 9个发射器和8个接收器的参数

此外，BR中的测量噪声服从零均值的高斯分布，且已知方差[10],其仅依赖于每对发-收的信噪比。因此，BR的测量值只受加性高斯噪声影响，其标准方差σi,j=σ0rt,irr,j/R0，i=1,…,M,j=1,…,N，其中σ0为常数，R0为监测区域半径。

同时，将选择文献[10]的OSWLS、文献[7]的WLS算法、文献[8]的TSWLS和文献[8]所推导的CRLB算法作为参考，并已对本文所提出的ICWLS算法进行比较。并选择均方根误差(Root Mean Square Error, RMSE)作为性能指标，其定义如式(25)所示：

(25)

3.1 实验一

本次实验分析目标x0位于[100 400 200]T时的ICWLS定位性能，且R0=600 m，实验数据如图2所示。

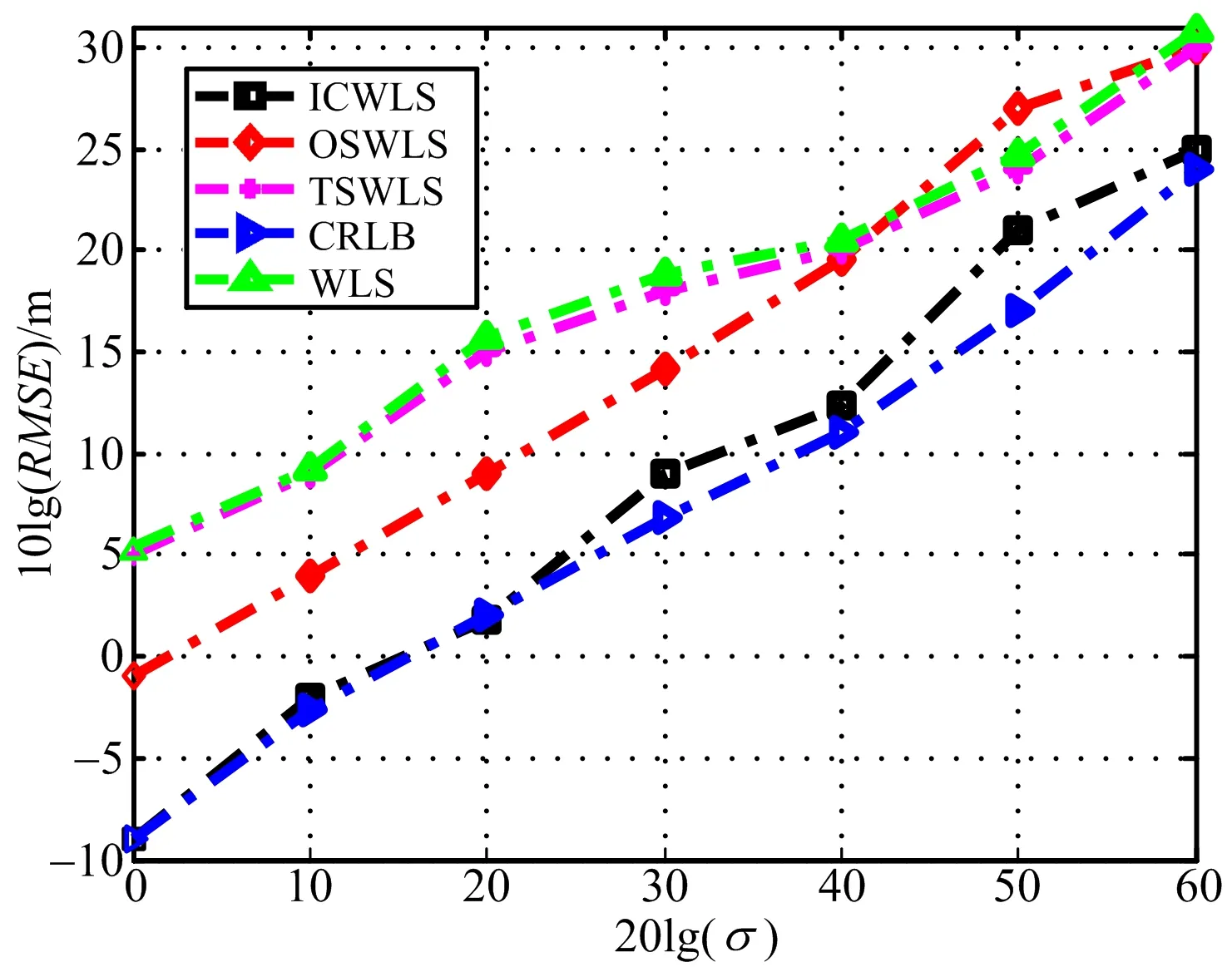
图2 实验一RMSE

图2分析了各算法的RMSE随σ0的变化曲线，且σ0从1～1 000变化。从图2可知，相比于其他算法，提出的ICWLS算法具有更高的定位精度。此外，通过图2发现，在σ0从1～1 000变化期间，ICWLS的RMSE与CRLB精度一致。

3.2 实验二

本次实验中，目标位于平行y轴，且x0=400 m,z0=200 m,R0=600 m,σ0=40。实验数据如图3所示。

从图3可知，ICWLS算法的定位误差RMSE在y轴的变化期间仍低于其他算法，并且逼近于CRLB。与TSWLS算法相比，ICWLS算法的RMSE平均下降了约25%。

图3 实验二RMSE

4 结束语

本文分析了基于双基测距的单一目标的定位问题，并提出迭代的CWLS算法。首先将目标定位问题转化为QCQP，然后再将QCQP问题转化为LCQP问题，进而获取封闭解。最终通过ICWLS算法求解LCQP问题，进而估计目标位置。实验数据表明，提出的ICWLS算法能够有效地控制定位误差。

优化算法，降低算法复杂度，同时考虑多个目标而非单一目标的定位问题，这将是后期研究工作的重点。