基于空时频输出矩阵的盲波束形成算法

， ， ，

(陆军工程大学石家庄校区， 河北石家庄 050003)

0 引 言

阵列信号处理在无线通信、雷达信号处理、水声探测、医学诊断等领域都有广泛的应用[1-2]。例如在空地双基地雷达中，雷达系统由无人机搭载发射器，如果采用传统的脉冲追赶方式[2]，要求比较高的时间准确度和空间定位精度。但在实际情况中，由于空中平台的稳定度较低，发射波束指向不稳定，导致来波方向无法与实际情况相符，造成一定的空域覆盖损失。而盲波束形成算法只需要一定的先验信息而不需要训练数据，是阵列天线在复杂环境中有效工作的迫切要求。

现有的盲波束形成算法中，最常见的比如利用信号的恒模特性[3]、循环平稳特性[4]、高阶统计量特性[5]等。但是其主要适用于窄带信号的分析中。国内分析宽带信号的文献较少。其思路一般是将其理解为卷积混合盲源分离问题[6-7]，再利用盲解卷积算法进行求解。盲解卷积算法主要包括时域算法和频域算法两大类[8]。时域算法需要设计FIR滤波器达到解卷积的目的，而滤波器阶数上升会造成计算量大幅增加，并且系统的稳定性也是必须考虑的问题。频域算法主要是利用傅里叶变换，将时域问题转换为频域问题，将一个卷积混合问题转化为瞬时混合问题，利用时域上的盲分离算法如H-J扩展算法即可完成波束形成。但是由于各频点输出独立，存在子带输出排序上的模糊问题，导致性能下降。

文献[9-11]将时频分析理论应用到盲波束形成算法中，通过在时频域上的分析估计出导向矢量，在性能方面较之传统的波束形成有一定的优势，但是计算过于繁琐。本文从宽带信号的特性出发，利用分数阶模型分析提取信号。理论分析和仿真实验表明，在快拍数较少、信噪比较低的情况下，所提算法具有更好的有效性和稳健性。

1 信号模型

1.1 宽带信号模型

有M阵元的均匀线阵，以第一个阵元为参考原点，阵元间隔是d。假设有Q个线性调频信号入射到平面上，第m个阵元的输出为

(1)

式中,τm,q=(k-1)dsinθq/C,sq(t)=ejπ(2fq0t+μqt2),C为光速，τm,q为第q个信号关于参考阵元的延时，fq0为第q个信号的初始频率，μq为第q个信号的调频率，nm(t)为与信号无关的高斯白噪声，θq为第q个信号的入射角度。

写成向量的形式：

(2)

式中，第q个信号的导向矢量是

aq(t)=[1 e-j2π(fq0+μqt)τ1,qejπμq(τ1,q)2…

e-j2π(fq0+μqt)τM,qejπμq(τM,q)2]T

(3)

1.2 信号的分数阶域模型

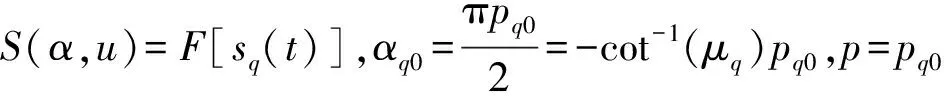
(4)

式中，T为观测时间长度。为了能在离散域进行计算，采用Ozaktas的离散算法[12]，得到离散的分数阶傅里叶变换。以采样率Fs对sq(t)完成时域上的离散：

s1,q(n)=ejπ(2fq0(n/Fs)+μq(n/Fs)2)

(5)

对其进行分数阶傅里叶变换，对应最优阶数αq0=-cot-1(μq)：

(6)

对每个阵元的接收数据进行最优阶次分数阶傅里叶变换，可得

Sm,q(αq0,km,q)=Am,q(τm,q)S1,q(αq0,k)

(7)

Am,q(τm,q)=ejπ/Nτm,q(-2kq0Fscscαq0)ejπ/N(τm,q)2(-Fs2sinαq0cosαq0)

(8)

综合所有阵元的输出可得

(9)

由于线性调频信号在最优阶的变换下除峰值点以外其他取值比较小，可以把它看作干扰项略去。改写为

X(αq0,km,q)=Aq,m(τm,q)Sq(αq0,kq0)+

Nm(αq0,km,q)

(10)

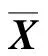
(11)

考虑到模型建立与实际情况的关系，下面的分析中做出以下3点假设：

1) 调频率不一样，可以将其分离；

2) 信号的来向不同，也就是导向矢量之间是相互独立的；

3) 采集到的信号是一个脉冲内的信号。

2 基于分数阶傅里叶域滤波的盲波束形成算法

对于线性调频信号而言，分数阶傅里叶变换具有独特的优势。在最优阶的变换下具有最好的能量聚集性。据此可以把信号的能量集中于很小的一个部分，通过滤波的方式获得信号的大部分能量，根据这些信息便可以很好地估计出实验需要的导向矢量，再根据波束形成算法对特定的方向完成接收和抑制的作用。

2.1 分数阶傅里叶域峰值滤波

通过上述分析可知，在最优阶数下，线性调频信号在分数阶域会出现能量的聚集效应，也就是会出现单峰值点，这个峰值就是线性调频信号在分数阶域的表示，它包含了线性调频信号的所有信息，如图1所示。据此，可以构造一个峰值滤波器，最大限度地分离特征不同的信号，并且滤除噪声。

(a) 有用信号在不同阶下的幅值分布

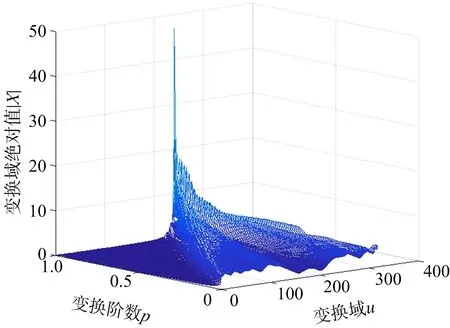
(b) 干扰信号在不同阶下的幅值分布图1 不同信号的幅值分布图

2.2 导向矢量的估计

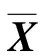
(12)

(13)

由式(13)可得每个信号的估计导向矢量，其中q表示第q个信号，m表示第m个阵元。

2.3 干扰协方差矩阵

滤波后得到的干扰信号同样对其作分数阶域的峰值滤波，得到与有用信号导向矢量估计相似的干扰导向矢量估计，而对其作协方差的运算即可得到MVDR准则中的关于分数阶域的空时频输出矩阵协方差矩阵：

(14)

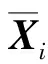
计算时为了提高整个系统的稳健性，采用文献[13]中提到的对角加载技术改造协方差矩阵，如下式：

(15)

式中，load表示加载系数，具体数值根据环境中的信噪比确定。

2.4 波束形成

根据MVDR波束形成理论，得到导向矢量和干扰协方差矩阵，如下式计算权值：

(16)

根据Lagrange乘数法，可以得到最终需要的最优权矢量，通过最优权矢量便可以形成所需要的波束：

(17)

2.5 算法分析

文献[8]的运算主要集中在时频变换的计算上，本文算法的计算量主要集中在分数阶域滤波上，利用FFT算法可以极大程度地减少运算量，提高运算效率。具体运算量对比如表2所示。

通过分析可知，文献[8]算法随着N的增大快速增加，而本文算法利用FFT算法可以很好地降低运算量，且FFT算法在工程实践中已经有成熟的算法，所以该算法在工程实践中有更好的应用前景。

表1 本文算法

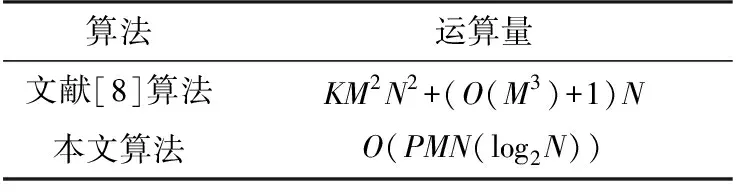
表2 运算量对比分析

注：P表示需要做P次(本文取100次)的分数阶傅里叶变换，M表示阵元数，N表示采样点数。

3 实验仿真结果与分析

考虑有8个阵元的均匀线阵，阵元间距是信号最小波长λmin的一半，为了不失一般性，有两个远场信号射入。假设一个是宽带信号s1，入射角是-25°，调频范围是90～100 MHz，中心频率是95 MHz，相对带宽满足宽带条件。另一个是宽带信号s2，入射角是0°，中心频率是142.5 MHz，调频范围是135～150 MHz，相对带宽满足宽带条件。输入干噪比等于输入信噪比。设置不同的仿真条件，假设s1是有用信号，s2是干扰信号，进行100次蒙特卡罗实验，将本文算法与频域[8]以及时频域[9]算法进行对比，分析总结算法性能。

实验一 不同输入信噪比下的输出信干噪比

实验条件是信噪比由-20～20 dB，步长是 5 dB，采样频率是400 MHz的情况下。比较本文算法与频域[8]算法以及时频域[9]算法的输出信干噪比随输入信噪比的变化趋势。仿真结果如图2所示。

“统一战线具有内蕴的共同体理论基因、丰富的共同体表现形式、独特的共同体力量功能，这是统一战线成为我们党的重要法宝的理论原理所在。”［9］由于统一战线是政治联盟，统一战线所构建的共同体主要是政治共同体。统一战线与共同体的逻辑关联表现在以下三个方面：

如图2所示，在信噪比较低的时候，由于分数阶傅里叶变换具有较好的能量聚集性，本文算法可以较好地识别信号。而频域和时频域的方法由于受到噪声的影响更大，恢复性能有较大限制。

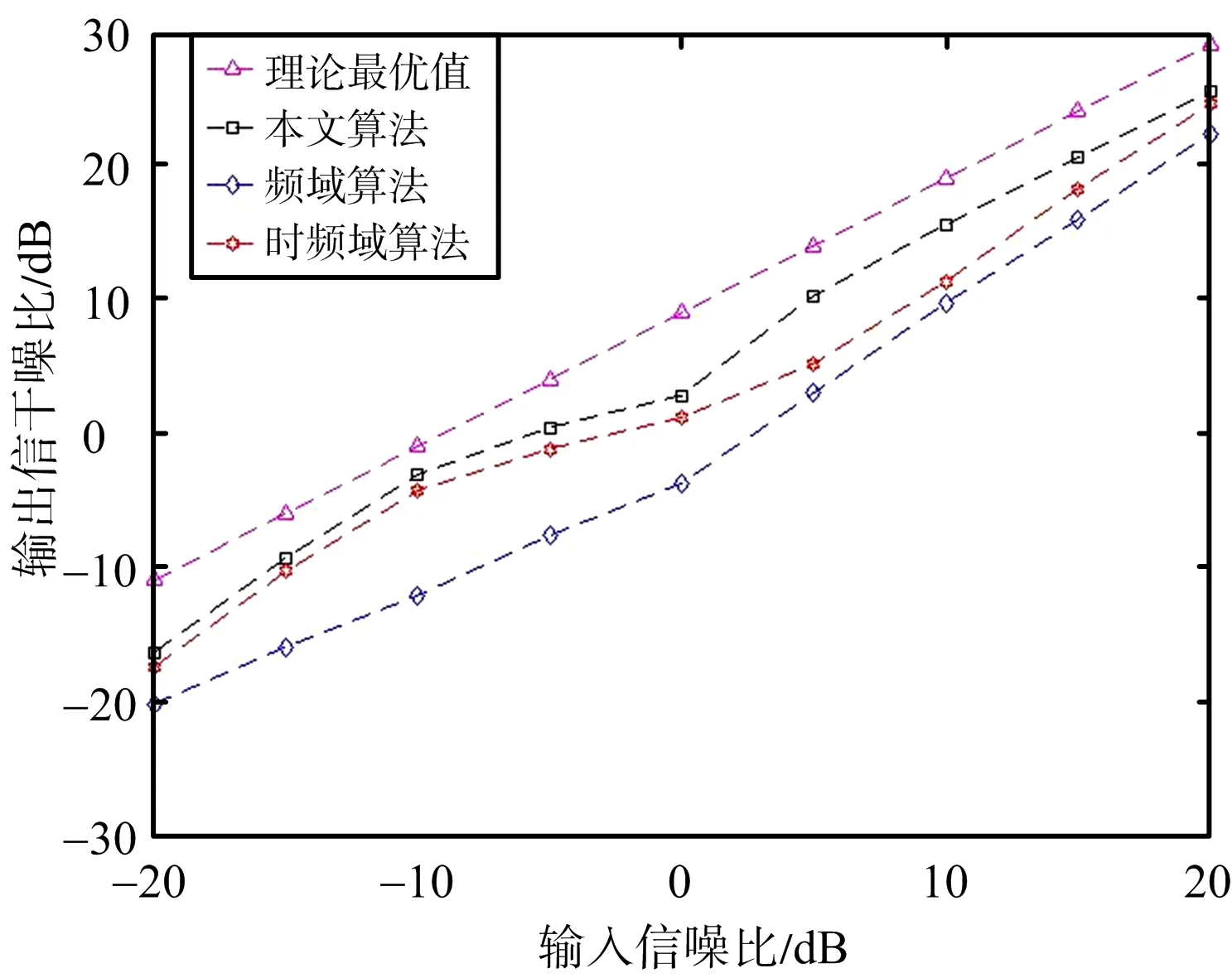
图2 输出信干噪比与输入信噪比的关系

实验二 不同快拍数下的形成质量

在同样的信噪比(SNR=10 dB)下,设置不同的采样率从100～400 MHz，快拍数分别是80,120,160,200,240,280,320。比较时频域[9]的算法和本文算法在不同快拍数下的区别，仿真结果如图3所示。

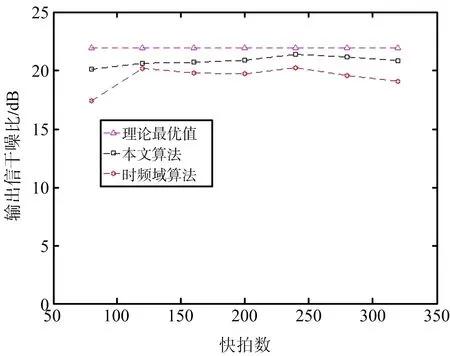
图3 不同快拍数下的输出信干噪比

如图3所示，在低快拍数的情况下本文算法具有较好的性能，时频域算法的性能要略差一些。

实验三 波束形成的鲁棒性仿真分析

在导向矢量误差为1°的情况下，设置信噪比是-40～40 dB，步长是5 dB，采样频率是400 MHz。比较本文算法与频域[8]、时频域[9]算法的输出信干噪比随输入信噪比的变化趋势，仿真结果如图4所示。

通过图4可以看出，当估计导向矢量1°的误差时仿真的3种算法性能都有所下降，但是本文算法能随着输入信噪比的提高能较快地趋向最优，说明本文算法的鲁棒性较好。

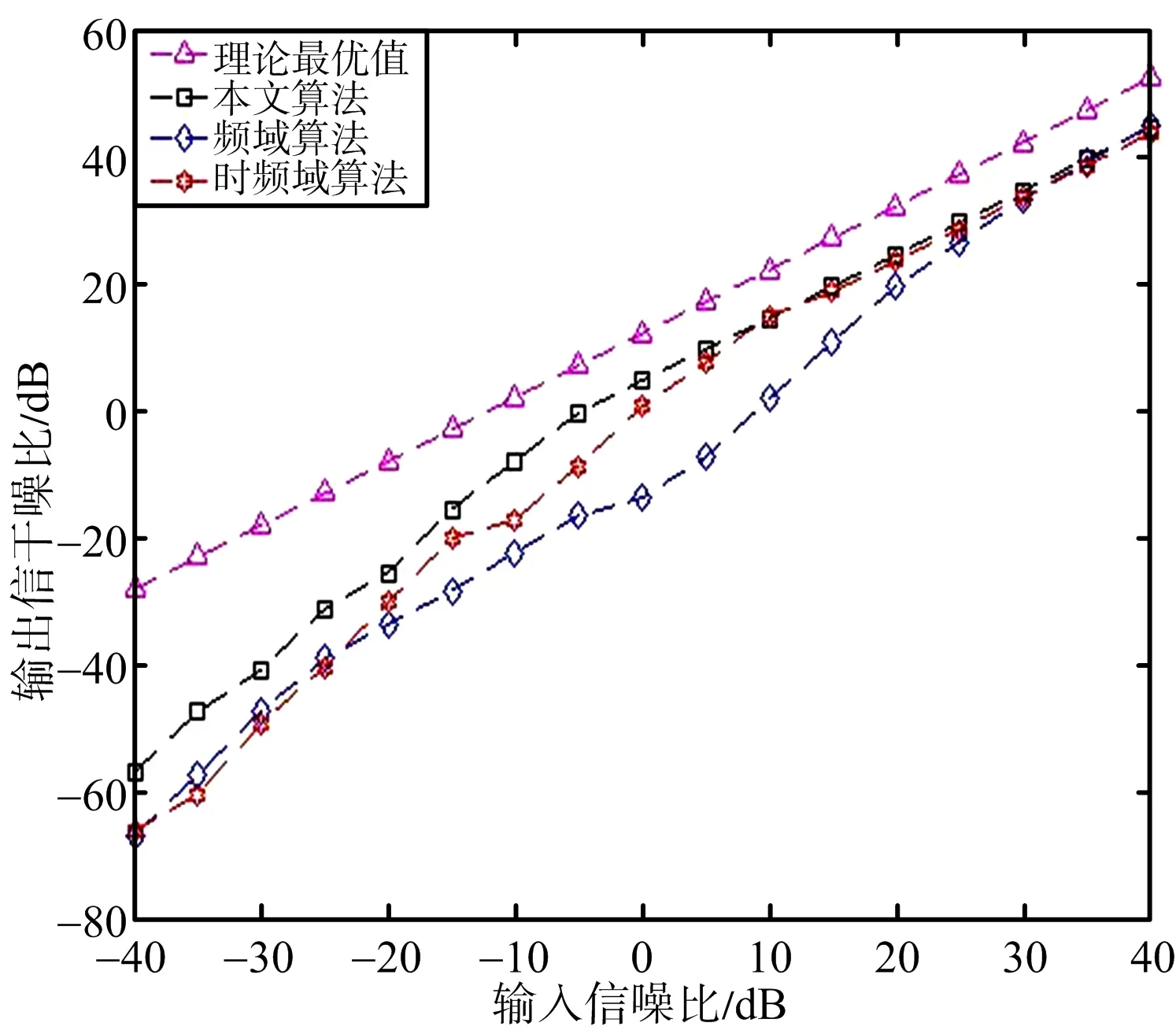
图4 导向矢量误差1°时的输出信干噪比

实验四 一定条件下的波束形成图

在信噪比(SNR=10 dB)下,设置采样率是400 MHz，入射角是-25°，调频范围是90～100 MHz，中心频率是95 MHz。根据本文方法计算波束图。

通过图5可以看出，本文方法形成的波束指向较为稳定，可以较好地接收信号。但是副瓣电平较高，接近-10 dB，对波束形成的稳定性造成了不良影响。

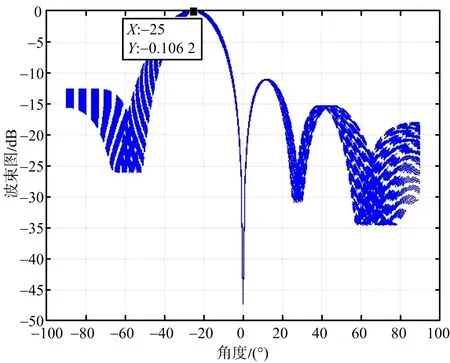
图5 波束形成图

4 结束语

波束形成算法中传统的时频分析方法计算量较大，当需要快速探测时，会有较大的迟滞。本文利用线性调频信号在分数阶傅里叶域具有能量聚集的特性，采用峰值滤波的方式构造空时频输出矩阵，并估计导向矢量，实现宽带信号的波束形成。实验结果表明，本文算法在低信噪比、计算量较少的情况下，可得到较好的输出性能。但是波束的旁瓣较高，需要进一步提高波束的稳定性，这也成为下一步的研究重点。