基于模型简化法的含有随机时延的多智能体系统一致性研究

张弘烨，彭世国

（广东工业大学 自动化学院，广东 广州 510006）

近年来随着计算机技术的迅速发展，多智能体协调控制问题引起了社会各界越来越多的关注[1-3]，在分布式编队控制[4]、神经系统稳定控制[5]、脉冲控制[6]等领域都得到了广泛应用. 多智能体系统一致性是协调控制的重要组成部分. 多智能体一致性指的是系统中所有智能体的信息最终趋于相同. 为实现多智能体的一致性，需要设计出能使各个智能体相互交换彼此信息从而实现所有智能体信息最终趋于相同的规则，即一致性协议.

目前，在多智能体系统一致性问题的研究中，许多学者已经取得了丰硕的成果. Vicsek等[7]从统计学角度出发，建立了经典离散时间模型. Olfati等[8]则对无向联通并且权值对称的多智能体系统进行研究，认为只要系统强联通，则多智能体系统就能实现一致性. 而Ren等[9]在文献[8]的基础上得到了有向拓扑的多智能体系统收敛条件.

然而在实际应用中，系统不可避免地遇到各种外界影响，例如网络堵塞或者其他因素等，造成通信延迟，从而导致智能体之间的信息传递存在一定时延. 针对这种现象，文献[10-13]对含有时延的多智能体系统一致性进行了广泛研究. 由于环境的复杂性，多智能体系统中智能体之间输入时延随机存在更具有普遍性. 本文受文献[14]的启发，研究系统中存在随机时延的情形. 文献中对含有时延的多智能体系统的分析一般利用线性矩阵不等式给出系统一致性的条件，但线性矩阵不等式法计算量大且复杂，不便于分析含有随机时延的多智能体系统. 本文将采用文献[15]提出的模型简化法对含有随机时延的的多智能体系统的一致性进行讨论.

1 预备知识

1.1 图论

令G(ν，ε，A)表示具有n个节点的有向图，ν={ν1，ν2，···，νn}表示图G 顶点集，ε⊆ν×ν表示图G 边集，A=[aij]表示图G 的邻接矩阵，若存在由节点νi到νj的有向边 eij∈ε，则aij＞0，否则 aij=0. 令矩阵D=diag{di，i=1，2，···，n}，其中为节点i的出度，则Laplacian矩阵L可定义为L=D-A.

假设1 Laplacian矩阵的0特征值是一个单一特征值.

对于网络连接，这个情形代表了这个网络存在一个生成树从而连接任意两个子系统，对于一致性协议的设计，只需考虑0特征值是单一特征值[16].

1.2 模型

本文考虑具有n个智能体的一阶多智能体系统，智能体之间的拓扑图用图G 表示，每个智能体可看作图G 的一个节点，且满足以下动态方程

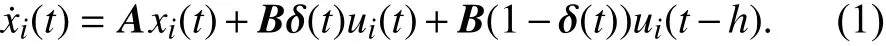
其中xi表示智能体 i的状态，ui则表示控制输入，A,B表示常数可控矩阵，h＞0表示系统输入时延，同时为了表征系统时延可能存在也可能不存在，引入变量δ(t)，当δ(t)=1时表示系统不存在时延，而δ(t)=0表示系统存在时延，其中δ(t)满足如下分布变换：

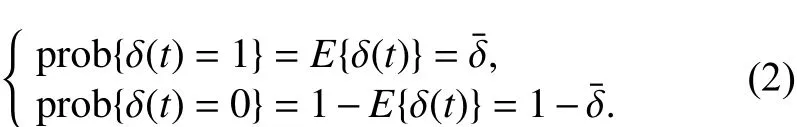
引理1 一个含输入时延的系统：

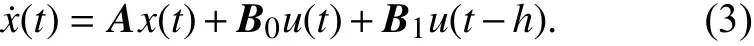
令

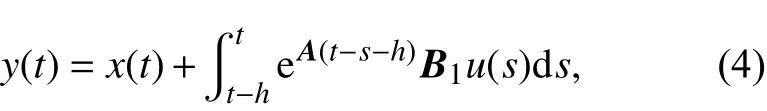
则原系统(3)稳定性与如下系统(5)相同,

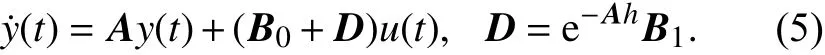
证明

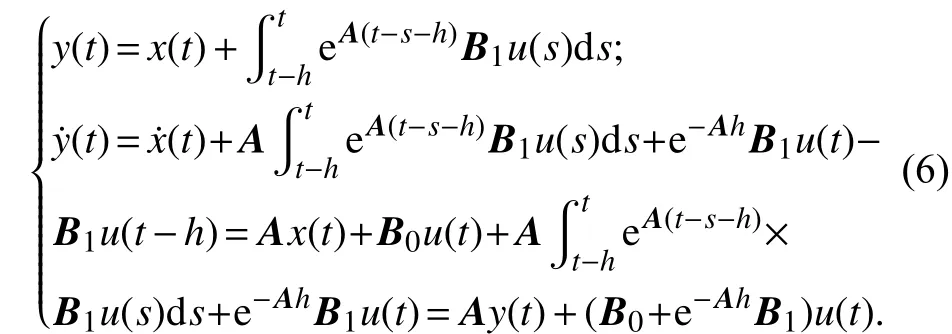
对系统(3)，提出以下控制器如果控制器(7)能使得系统(5)达到稳定，则原系统(3)也能用相同控制器达到稳定[17-18].

引理2[16]如果Laplacian矩阵L只含有一个0特征值，其余特征值均大于0，则存在一个相似变换T，同时T的第一列T(1)=ϕ, ϕ =[1，···，1]T使得

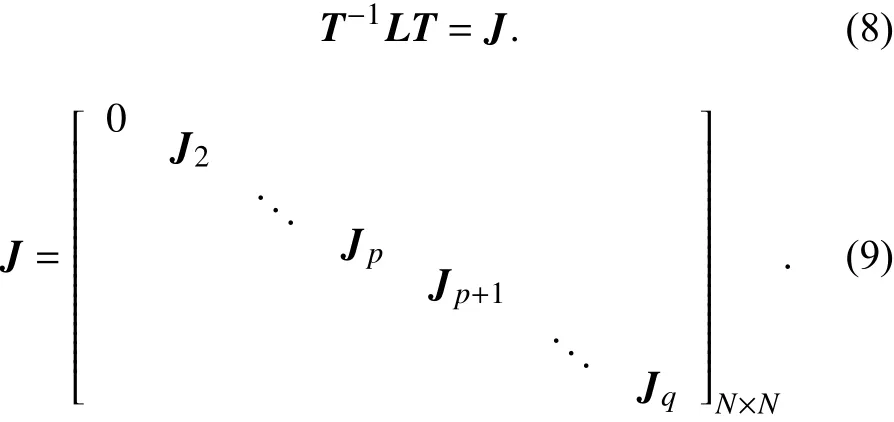
当Jk∈ Rnk×nk, k =2，3，···，p ，是Jordan块中的nk重实数特征值λk＞ 0的形式，即

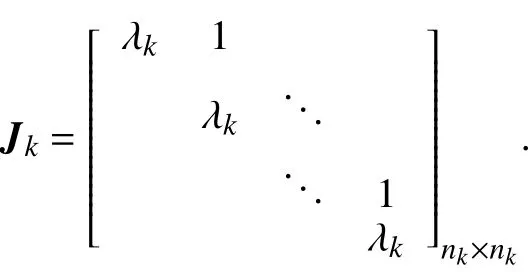
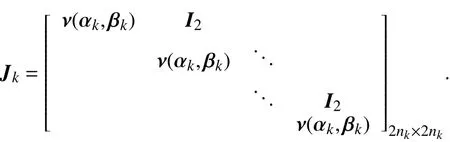
I2是R2×2的单位矩阵且

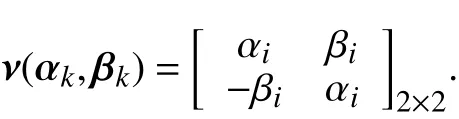
2 主要结果

根据引理1，对多智能体系统(1)，使用变换(4)作简化. 令

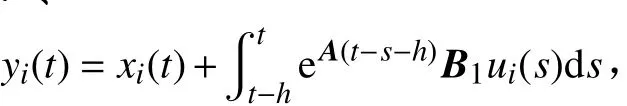
则系统(1)可转化为

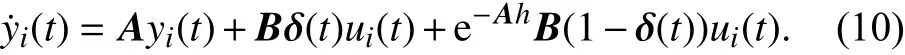
针对简化后的系统(10)，采用如下控制协议

其中，K表示控制增益.

定理1 当控制增益K满足

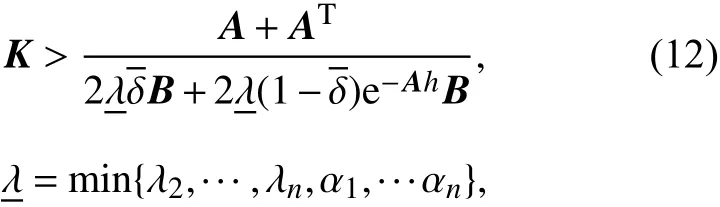
系统(1)可达到一致性.

证明 令

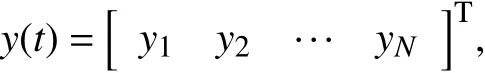
则系统(10)可写成

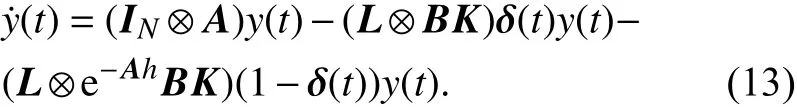
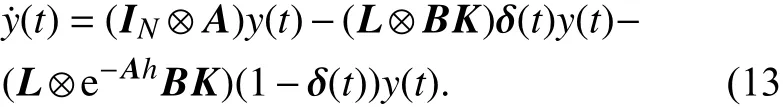
定义 r∈RN为矩阵L的0特征值对应的左特征值向量，即rTL=0，同 时 使 之 单 位 化 ，即 rTϕ=ϕ,ϕ =[1，···，1]T. 从 引 理2可 知 存 在 矩 阵T使 得T-1LT=J.

定义

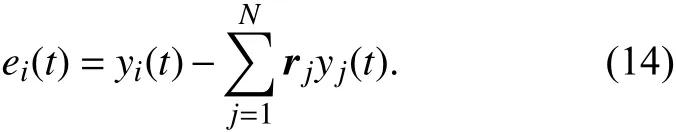
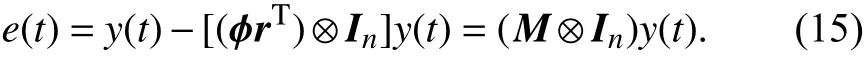
此时 M=IN-ϕrT. 由于 rTϕ=ϕ即 Mϕ=0，因此系统(13)的稳定性相当于e=0，因为此时相当于y1=y2= ···=yN，则一致性问题转化成了系统稳定性问题.

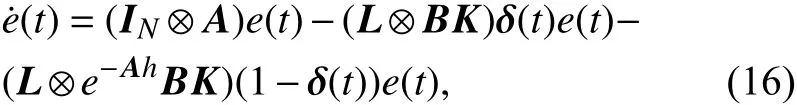
定义

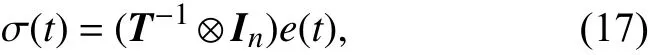
则

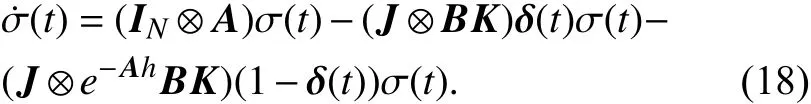
根据转化式(14)和(17)，

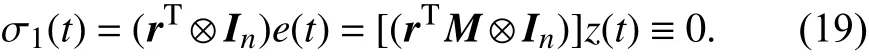
因此只需要证明 σi收敛到0，则可以证明一致性可达成基于laplacian矩阵的结构，可以发现

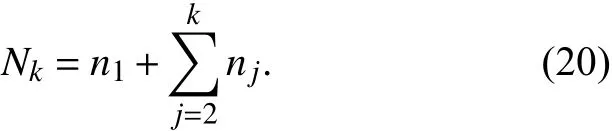
同时，n1=1, Nq=N，且k =2，3，···，q.

当Jk为实数特征值，即 2≤k≤p ，

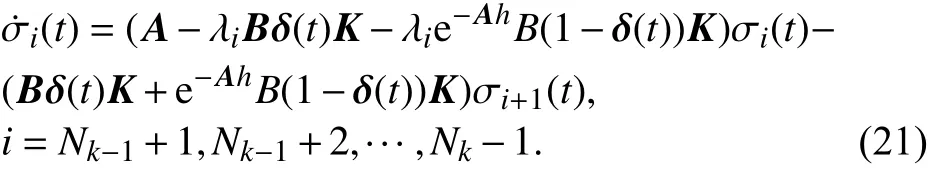
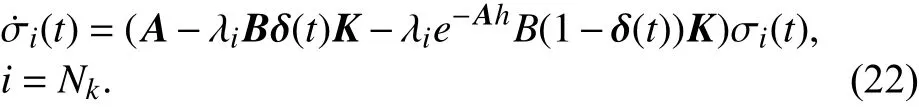
当Jk为复数特征值，即k＞p，可考虑一对动态状态方程，为方便，让

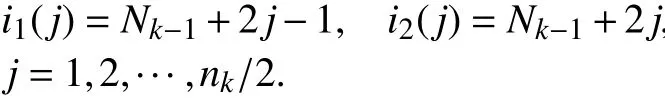
则当 j=1，2，···，nk/2-1，σi1(j)和σi2(j)的动态方程为

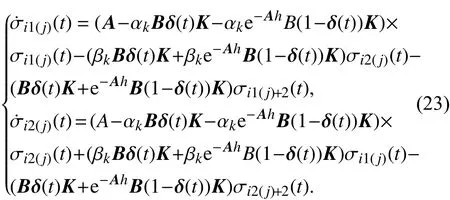
当 j=nk/2,

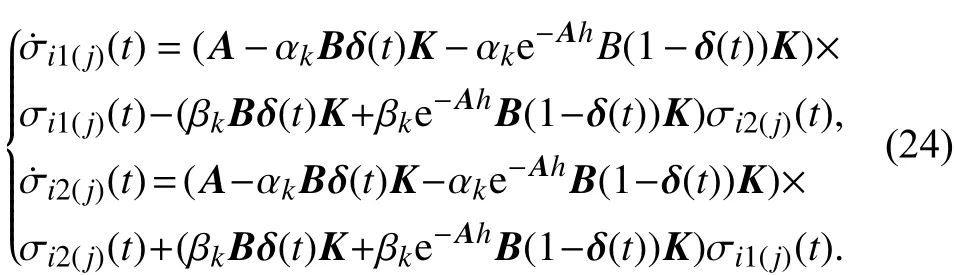
对于系统(8)构造如下Lyapunov函数

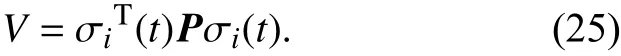
当i=Nk，V的导数为

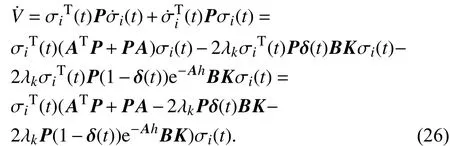
对等式两边求解期望，

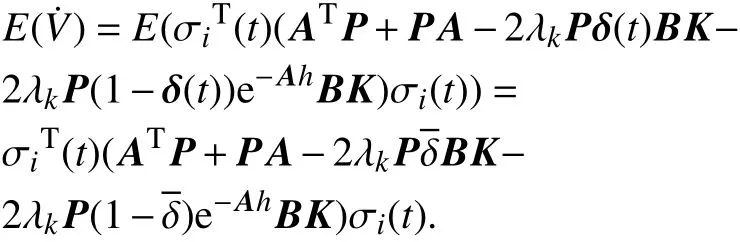
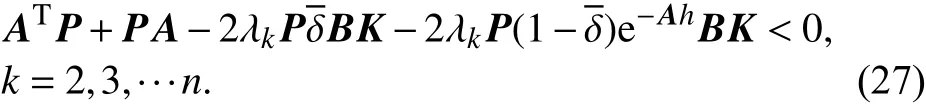
存在某个K值使得(9)恒成立. 由于 P＞0，即需要

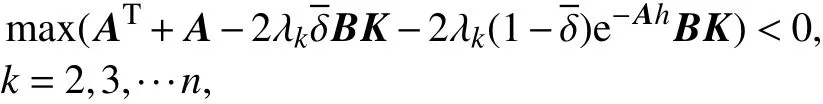
所以

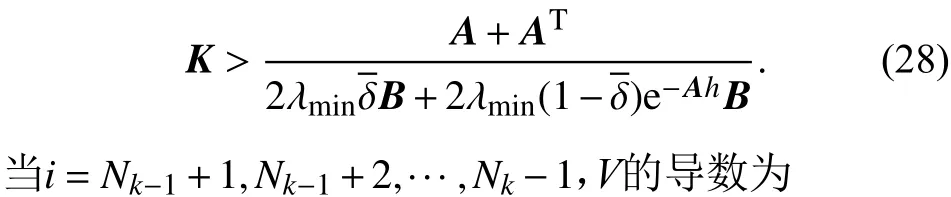
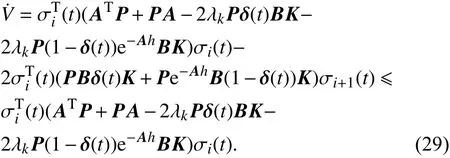
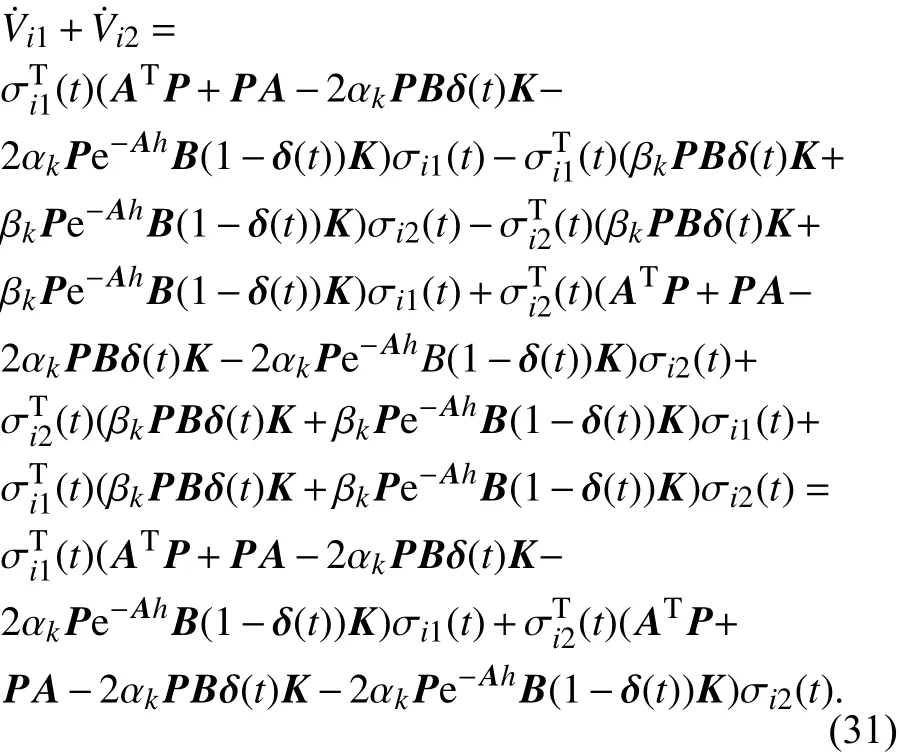
对两边求期望

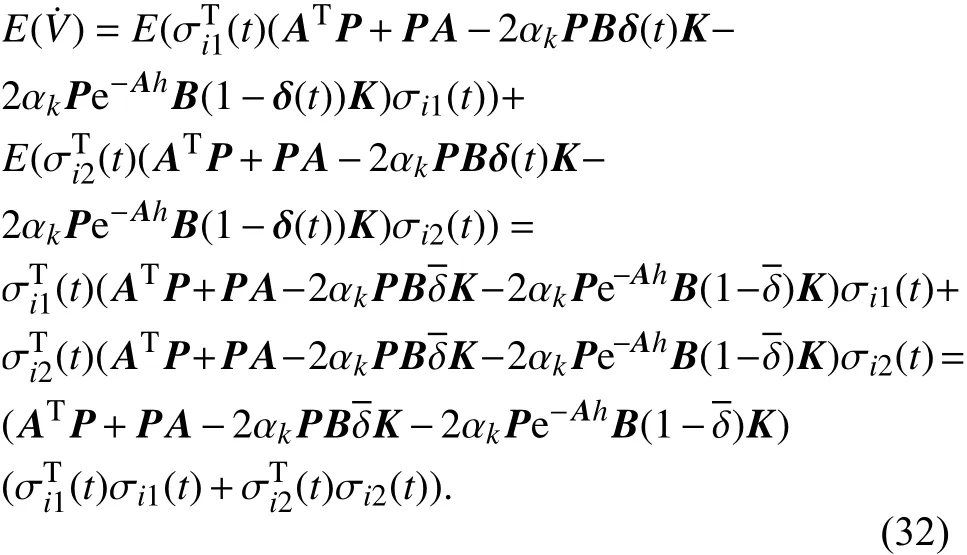
存在某个K值使得式(33)恒成立. 由于 P＞0，即

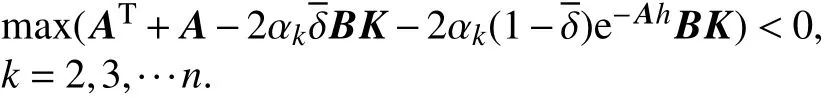
所以

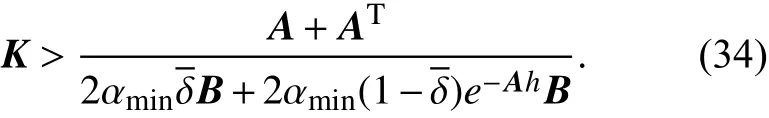
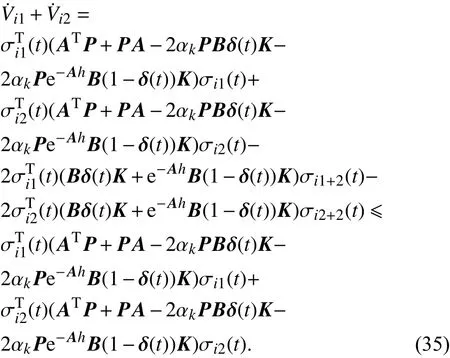
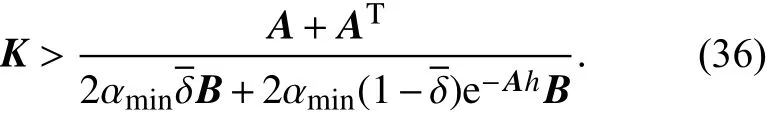
因此结合式(28)、式(30)、式(34)和式(36)，只要满足

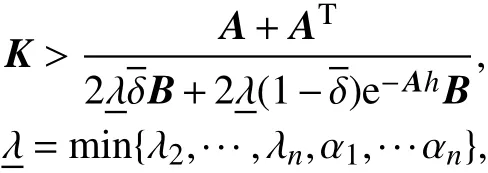
多智能体系统(1)可达到一致性.

3 仿真验证

如图1所示，假设多智能体系统拓扑图包含以下4个节点，分别记作节点1、2、3、4，令A=1，B=3任意选择初始状态 x1(0)=-20， x2(0)=-5， x3(0)=15，x4(0)=30， δ=0.8，时延h=0, 03，各智能体连接权重为1.

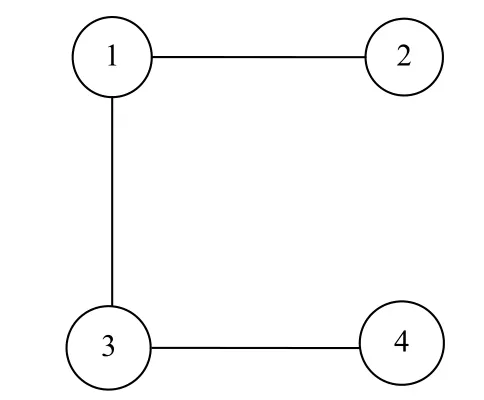
图1 系统结构拓扑图Fig.1 Topology of MAS

根据该拓扑图可写出Laplacian矩阵L，

可求得最小非0特征值 λ=0.5858,

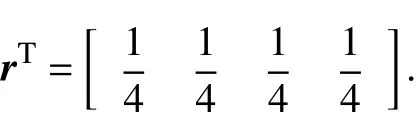
代入式(12)可得K ＞0.5724.

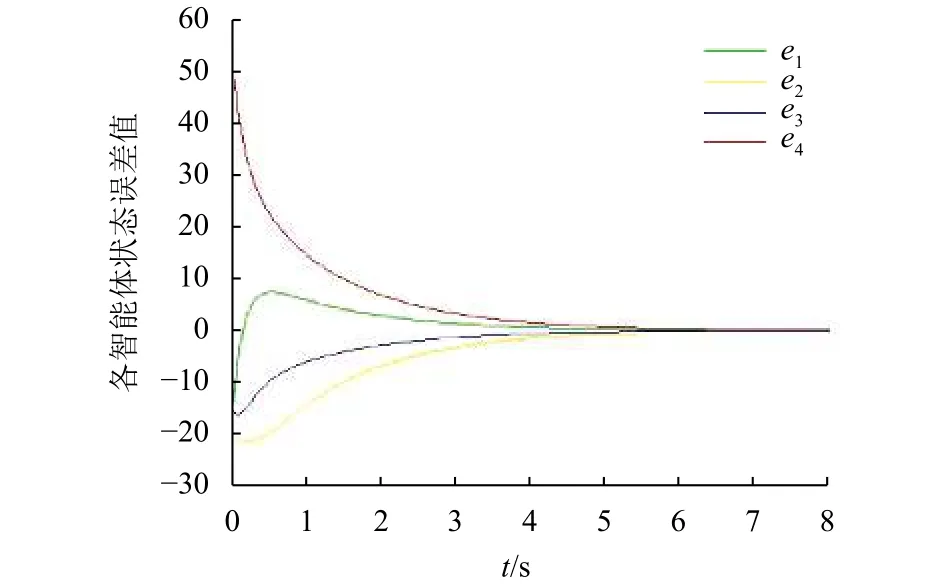
图2 K=1各智能体之间误差曲线Fig.2 The status errors of subsystems with K=1

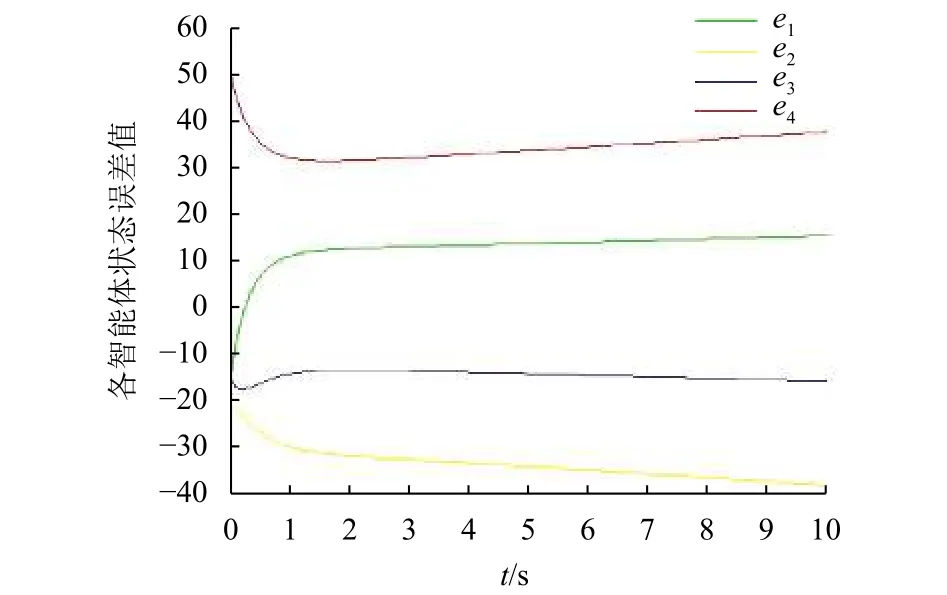
图3 K=0.562各智能体之间误差曲线Fig.3 The status errors of subsystems with K=0.562

当K=0.582略大于临界值，如图4所示. 可以看出当K值大于临界值时，各智能体误差曲线呈收敛趋势，经过一定时间能够收敛于0，各智能体能够达到一致性.

4 结束语

本文研究了一阶含随机时延的多智能体一致性问题，并通过模型简化法，引入一个新变量，将原本含有时延的系统转化为一个不含时延的系统，并提出一个一致性算法，使用Lyapunov函数，找出多智能体系统在这个算法下达到一致的充分必要条件. 最后给出模型仿真，验证出这个结论的正确性以及通过模型简化法对含有随机时延的多智能体系统分析的可行性.

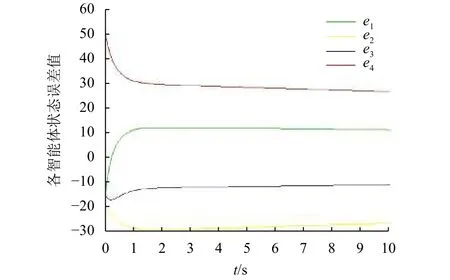
图4 K=0.582各智能体之间误差曲线Fig.4 The status errors of subsystems with K=0.582