基于IC卡数据的居民出行成本建模分析

谢振东，何建兵，何仕晔，吴金成，徐 锋，张景奎，冷梦甜

（1. 广东岭南通股份有限公司，广东 广州 510000；2. 广东工业大学 自动化学院，广东 广州 510006）

随着社会经济水平的不断提高，国民收入不断增加，越来越多的人开始拥有自己的车辆. 如今巨大数量的私家车给城市交通造成了拥堵，群众出行十分不便. 为解决城市交通拥堵的现状，发展公共交通是一条重要的途径[1].

发展公交出行的同时，需考虑居民出行的成本[2-4].文献[5-7]提出为构建旅客出行成本测度模型，从显性和隐性两个角度研究旅客出行成本的成本构成并进行成本测度，将出行成本分为直接购票费用、其他相关费用、时间成本、生理成本和心理成本5个方面.而针对交通客流信息的获取，文献[8-9]指出公交客流调查是一项繁琐和大量耗费人力、财力的工作，实际操作非常困难，采用基于公交IC 卡信息处理来获取公交客流信息是十分便捷有效的手段. 文献[1, 10-12]也使用公交IC卡大数据对公交客流等进行分析，达到了客流分析的目的.

在交通出行方面，许多研究更倾向于利用交通大数据进行客流预测或给予出行建议，而本文利用核密度估计算法对广州公交IC卡数据进行建模，并对模型的泛化能力进行测试，进而分析居民公交出行的时间成本和支出成本，以此为政府对公共交通相关政策的制定提供建议.

1 核密度估计

就居民出行成本的分析，在此使用的是核密度估计算法. 核密度估计(Kernel Density Estimation )是在概率论中用来估计未知的密度函数，属于非参数检验方法之一，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗(Parzen window).

一般对于参数模型的这种基本假定与实际的物理模型之间常常存在较大的差距，这些方法并非总能取得令人满意的结果. 而核密度估计完全利用数据本身信息，避免人为主观带入的先验知识，从而能够对样本数据进行最大程度近似(相对于参数估计法).

由于核密度估计方法不利用有关数据分布的先验知识，对数据分布不附加任何假定，是一种从数据样本本身出发研究数据分布特征的方法，因此在统计学理论和应用领域均受到高度的重视.

核密度估计是一种用于估计概率密度函数的非参数方法， x1、x2、x3···xn为独立同分布的n个样本点，设其概率密度函数为f，核密度估计为以下[13-14]：

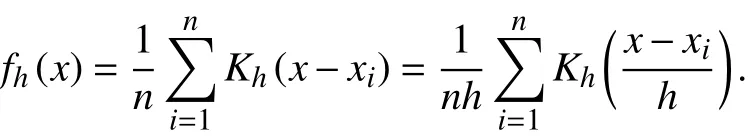
其中K为核函数，与支持向量机(SVM)、meansift等算法中的核函数类似，核密度估计中常用的核函数有Uniform函数，Triangular函数，Biweight函数，Triweight函数，Epanechnikovnormal函数等. h为平滑参数，称为带宽，不同的带宽会导致最后的拟合结果差异很大，h选择得太小，领域中参与拟合的点就会过少，而h选择得太大，就可能发生波形融合. h 的选择视具体情况而定，如果认为拟合出来的概率分布曲线过于平坦，可以适当降低h参数，如果认为拟合出的概率分布曲线过于陡峭，则可以适当增大带宽h.

2 出行成本分析的技术研究

2.1 出行成本的概念

成本是指为了完成某个特定的任务或者达到某个目的所需要付出的代价. 出行成本是指为了完成人或者物品在空间位置上转移所需付出的经济成本和时间成本的总和.

2.2 数据来源

本文建模时使用了广州公交地铁部分IC卡交易数据，共计543万条交易记录，其中公交出行交易记录246万条，地铁出行交易记录297万条，涵盖了工作日和非工作日，具有一定的代表性.

模型测试时，随机抽取了3 d的数据作验证，共计295万条，其中公交出行交易记录共128万条，地铁出行交易数据共167万条.

2.3 分析框架的选择

众所周知，交通出行刷卡数据量比较庞大，经试验，一般的数据分析工具由于效率不高，无法达到分析要求. 因此，本文针对海量数据分析特征采用了Apache Spark + Hadoop Hive框架.

Hive是建立在Hadoop上的数据仓库基础构架.它提供了一系列的工具，可以用来进行数据提取转化加载(ETL)，这是一种可以存储、查询和分析存储在Hadoop中的大规模数据的机制. Hive定义了简单的类SQL查询语言，称为HQL，它允许熟悉SQL的用户查询数据. 同时，这个语言也允许熟悉MapReduce开发者的开发自定义的Mapper和Reducer来处理内建的Mapper和Reducer无法完成的复杂的分析工作.

Apache Spark是专为大规模数据处理而设计的快速通用的计算引擎. Spark是UC Berkeley AMP lab(加州大学伯克利分校的AMP实验室)所设计的开源的类Hadoop MapReduce的通用并行框架，是一个通用引擎，可用它来完成各种各样的运算，包括SQL查询、文本处理、机器学习等.

使用Apache Spark + Hadoop Hive框架，能够利用Spark以代码的形式对Hive数据库进行Hive SQL查询，并将查询结果返回为方便处理的DataFrame类型，而无需进行Hadoop的Mapper和Reducer这一套复杂的操作. Apache Spark + Hadoop Hive框架能够有效地节约代码编写时间，并且能够充分发挥两者的优点，拥有良好的数据处理速度.

2.4 数据预处理

在分析出行成本之前，需要对数据进行处理. 海量的原始数据中可能会存在不完整(有缺失值)、不一致或有异常的数据，会严重影响到核密度估计建模的执行效率，甚至可能导致挖掘结果的偏差，所以进行数据清洗显得尤为重要，数据清洗完成后就是进行或者同时进行数据集成、转换、规约等一系列的处理，该处理过程就是数据预处理. 数据预处理一方面是要提高数据的质量，另一方面是要让数据更好地适应特定的挖掘技术或工具.

从各个地市得来的交易记录数据并不能直接用来进行数据分析，需要进行数据的预处理，具体操作如下[15]：

(1) 对于存在缺失、不完整、不合理(例如离群数据)的数据进行处理. 由于数据集样本充足，而存在以上情况的数据数目一般相对较小，可以进行舍弃.

(2) 公交卡存在不同的卡类型，大约80种，需要对其进行自定义划分，最终划分为三类：老年卡，学生卡和普通卡.

(3) 需要对来自不同地市的交易记录加入地区编码，用以区分.

(4) 对各地市的交易记录的数值进行数据规约，例如交易日期与时间需要处理成符合处理条件的格式、票价需要转换成Apache Spark相关操作需要的数据类.

本文对IC卡数据的预处理使用python的pySpark模块，pySpark模块是Spark的pyhton语言实现，将IC卡数据读成DataFrame的形式，以对其进行方便的处理.

2.5 出行成本建模研究

居民出行的成本一般体现在出行支出成本和出行时间成本两个方面，因此，本文正是基于以上两方面进行建模，建模使用核密度估计算法，能够客观地对样本数据进行最大程度的近似(相对于参数估计).在数据建模之前，首先需要为待训练的数据拟定特征和标签.

经分析，影响出行支出成本的因素主要包括出行方式(公交或地铁等，本次研究使用的数据仅包含公交和地铁交易数据)、所在地市区域(不同地区的票价花费、优惠政策等可能存在不同)、公交卡类型(不同类型公交卡存在不同的优惠方式)，因此核密度估计算法在出行支出成本分析中选取的特征应主要包括：出行方式、所在地市区域、公交卡类型、交易日期时间和交易金额，前4项作为出行支出成本分析的区分条件，交易金额作为核密度估计算法的输入.

影响出行时间成本的因素主要有出行方式(若出行时间不在居民出行高峰期，地铁相对于公交来说一般更快)、出行时间(居民出行存在高峰期，如上下班、节假日等，不同的时间段对出行的时间成本存在影响)、所在地市区域(不同城市的人口数量、人群类型数量、经济发展程度等都对出行时间造成影响)，因此核密度估计算法在出行时间成本分析中选取的特征应主要包括：出行方式、所在地市区域、公交卡类型、交易日期时间和出行时间，前4项作为出行时间成本分析的区分条件，出行时间作为核密度估计算法的输入.

在出行支出、时间成本分析中，核密度估计算法的输出能够分别体现不同时间、地区等条件下居民出行的消费密度与时间密度.

3 出行成本建模

3.1 出行支出成本模型构建与分析

3.1.1 模型建立

国家给予苗族银饰传承人一定的资金帮助促进其发展传承，同时组织相关人员将苗族银饰的制作流程整理成册并且出版发行。此外，国家完善了相关法律制度，形成了一套各级政府相辅相成的管理发展体制。

对于核密度估计算法，首先需要确认带宽参数，以广州公交地铁票价为例，出行方式的最小出行支出成本级差为0.6元(一般出行票价均以1元为单位递增，15次以后6折)，而带宽代表计算概率密度时所覆盖的范围，若过大则会让概率密度曲线更平缓，较难看出各个出行支出成本的概率密度差异，若过小，则会让差异显得太过突出，影响判断. 故在0.6附近取支出成本带宽h，核函数为Epanechnikov曲线，样本数量n为5 435 883，出行支出成本的模型为：

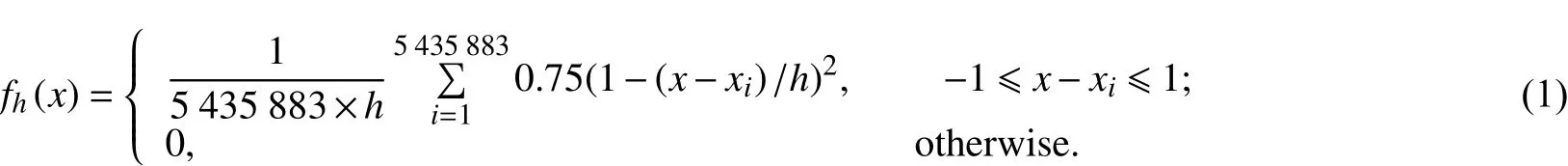
当h分别取0.4，0.5，0.6，0.7，0.8时，对其输出的概率密度积分，都能得到相应的概率，表1是8种出行支出范围的概率，图1是其各自的核密度曲线.

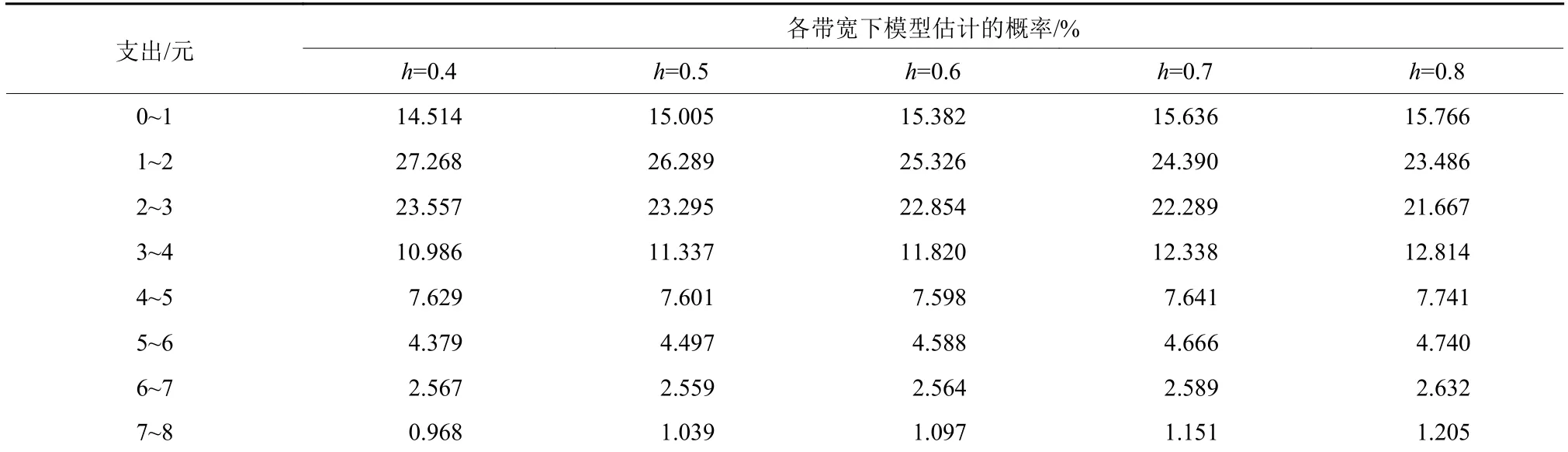
表1 模型估计概率表Tab.1 Model estimation probability

3.1.2 模型评估

为验证核密度估计算法模型的准确性与合理性，使用训练数据集的数据进行测试评估.

验证方法为：计算训练数据集分别在各个支出范围内的概率，与模型估计的相应支出范围的概率进行对比，计算得到平均偏差，训练数据集统计得到的频率(由于样本集足够的庞大，足以将频率近似为概率)如表2所示，相应的偏差值如表3所示.

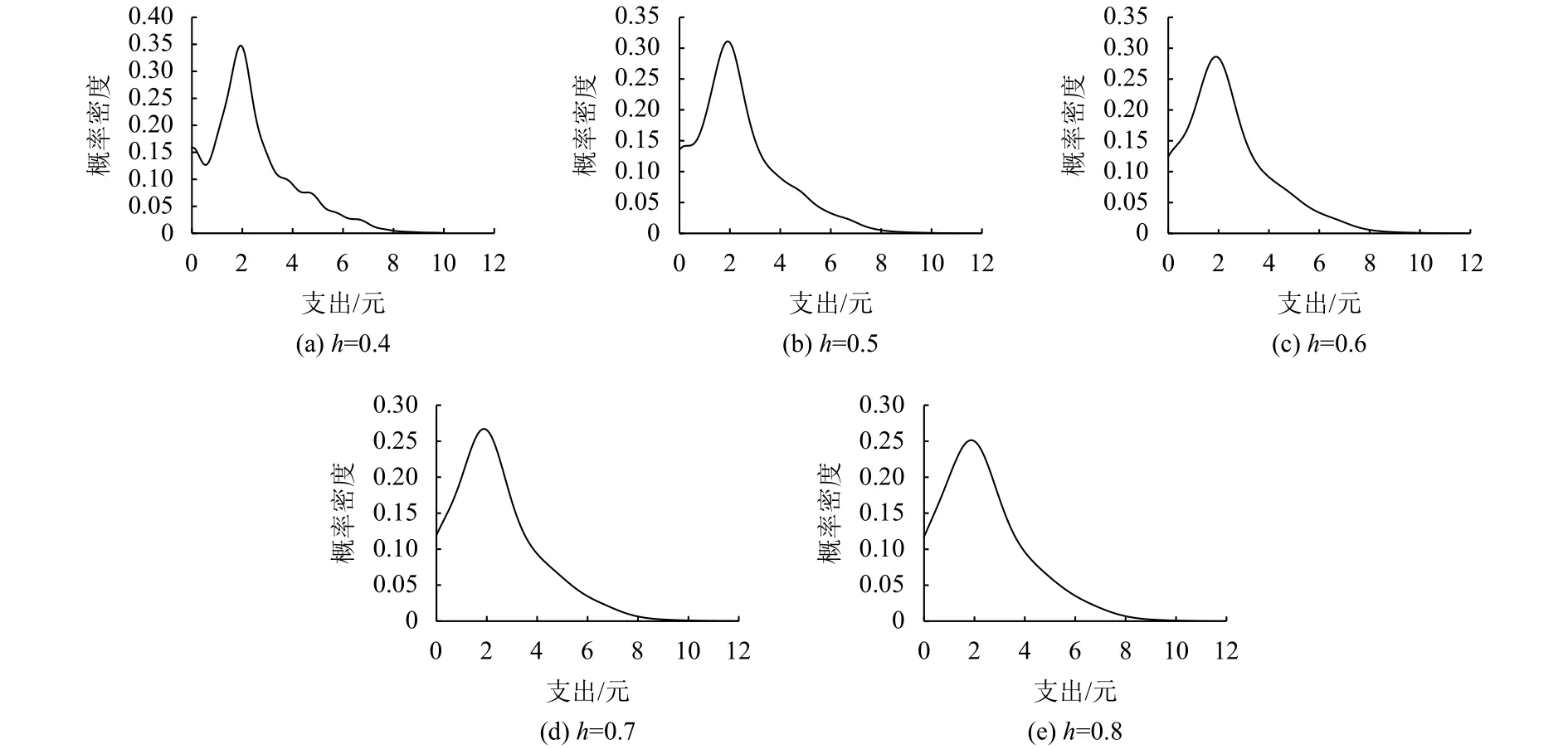
图1 各带宽h下的支出成本核密度曲线图Fig.1 The kernel density curve of expenditure cost under each bandwidth h

表2 模型估计概率表Tab.2 Model estimation probability

表3 偏差值表Tab.3 The deviation value

可以看出，带宽h取值越小偏差越小，精度越高，但是其相应的核密度曲线图越不平滑；当h取0.6时，曲线相对平滑、偏差也相对较小，这种偏差是允许的，如果算法模型的偏差太过于小，便说明模型呈过拟合，泛化效果便相对较差. 因此h取0.6作为带宽是相对合适的.

3.1.3 模型泛化能力测试

计算可得模型估计概率与测试集概率的平均偏差为3.658%，说明模型泛化能力良好，能够客观、准确地反映广州居民出行支出成本的现实常态.

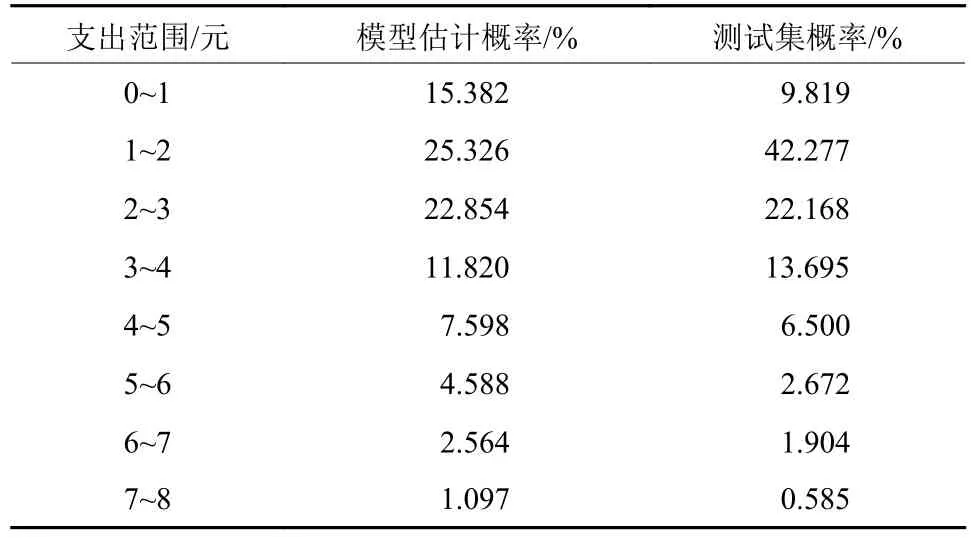
表4 模型估计的概率与实际概率对比表Tab.4 Model estimation probability and actual probability

3.1.4 模型分析

根据广州市统计局最新报告，2016年广州市城镇居民可支配收入为4 245元/月，而从2018年7月1号开始，广州市的月最低工资标准也升为2 100元/月.而当出现支出成本占收入的3%～5%时，公共交通出行幸福指数是最好的；超过5%指标时，则表明公众承受的票价压力较大，建议政府加大票价补贴，惠及大部分人群出行.

就广州市城镇居民可支配收入水平而言，每月合理的出行支出成本范围是127.35～212.25元，而根据出行支出成本核密度曲线以及上节的表格可以得出，居民公共交通出行票价基本保持在0～8元之间，对相应支出范围上下限的均值以概率加权并累加(例如0～1元范围的概率是15.382%，则其加权值为(1+0)×0.154/2)，便能得到平均出行支出为2.285元，以1月30天，每天2次计，则月均出行支出约为137元，符合合理出行支出成本范围，证明大部分广州市居民的公共交通出行支出成本幸福指数已经达标.

就广州市月最低工资标准而言，每月合理的出行经济成本范围是63～105元，而居民的月均出行支出为137元，并不能完全满足合理范围. 需要政府加大对最低工资人群的补助，以提升其公共交通出行经济成本幸福指数.

3.2 出行时间成本模型构建与分析

3.2.1 模型建立

对于核密度估计算法，需要确认的参数为带宽，一般来说，各种出行方式的出行时间均以分钟计，故在1.0左右为时间成本带宽h取值，核函数为高斯曲线，样本数量n为2 971 884个，出行时间成本的模型为：

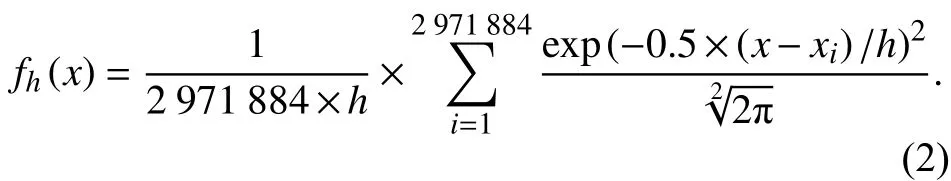
当h分别取0.5，1.0，2.0，3.0，4.0 时，对其输出的概率密度积分，能够都到相应的概率，表5是8种出行时间范围的概率，图2是其相应的核密度曲线.

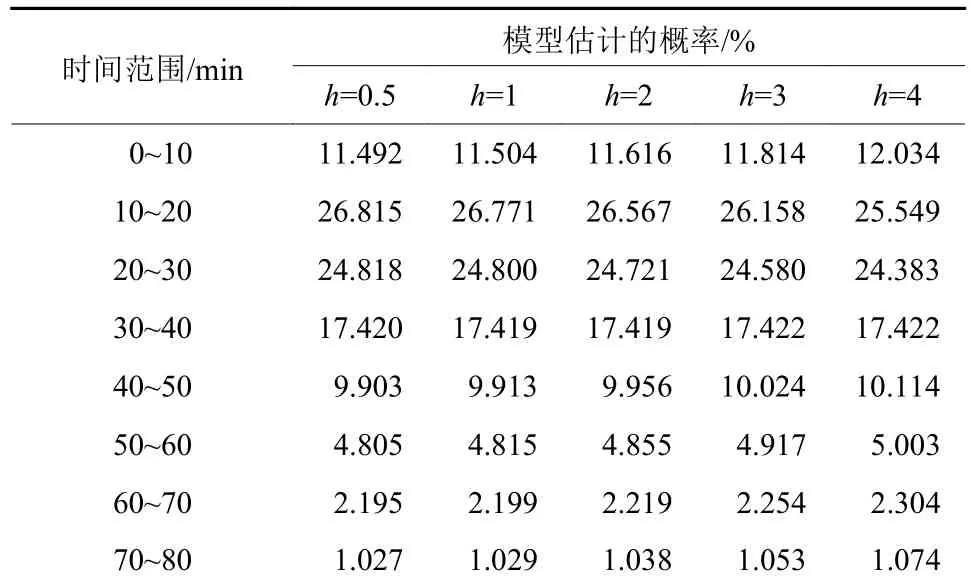
表5 模型估计概率表Tab.5 Model estimation probability

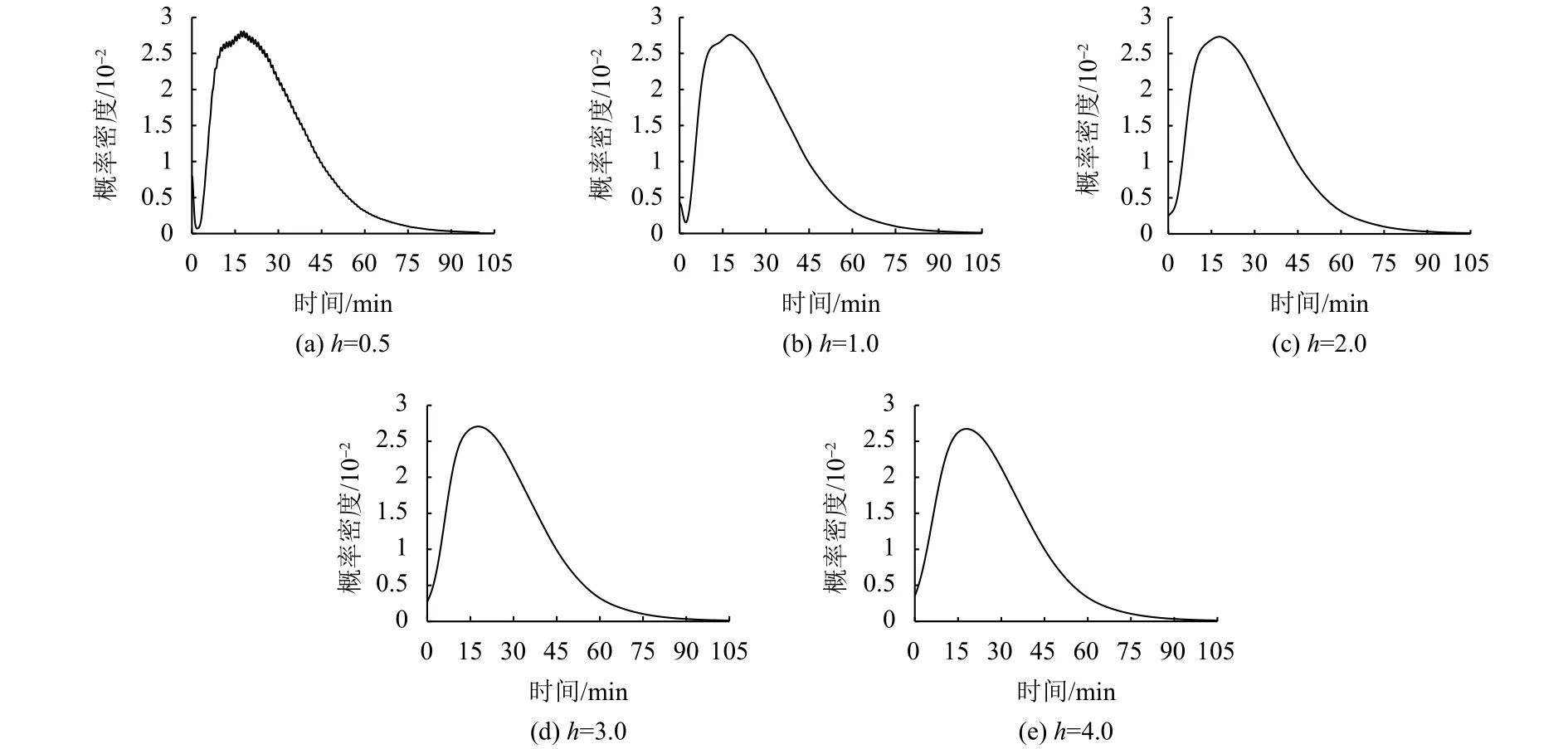
图2 各带宽h下的时间成本核密度曲线图Fig.2 The kernel density curve of time cost under each bandwidth h

3.2.2 模型评估

为验证核密度估计算法模型的准确性与合理性，使用训练数据集的数据，统计各个时间范围的频率(样本足够大，故可看做概率)，相应时间范围的频率如表6所示.

验证方法为：使用训练数据集分别计算各个时间范围的时间成本概率，并对模型估计的概率密度进行积分，算出相应时间范围的概率并得到偏差，如表7所示.

在以上各个带宽下，总偏差均比较小，而且当带宽大于1时，偏差随带宽增大而逐渐增大，而从核密度曲线可以观察到h为3时，曲线更平滑而有弧度，故取带宽h为3相对合适.

3.2.3 模型泛化能力测试

测试数据集为样本数据集随后3 d的数据，共167万条，模型估计的概率和实际概率如表8所示.

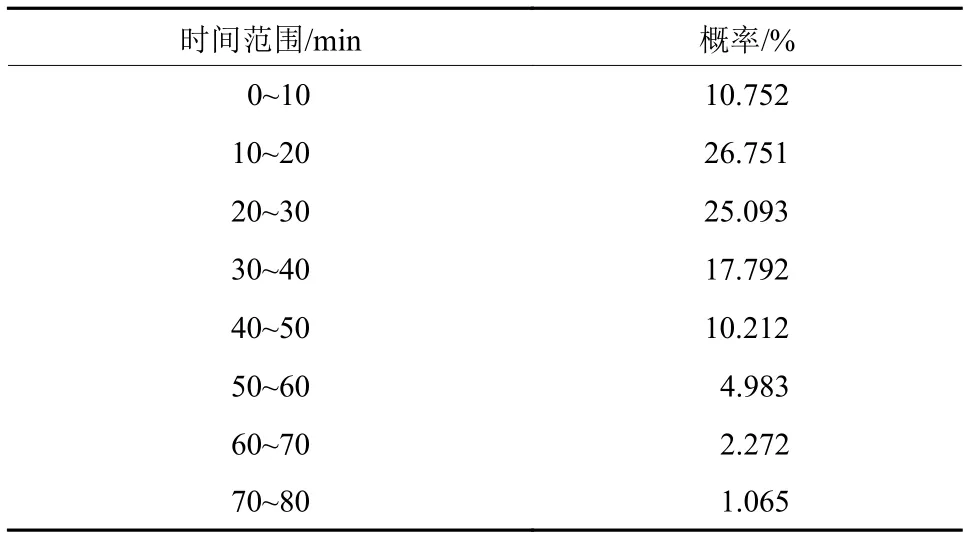
表6 模型估计概率表Tab.6 Model estimation probability

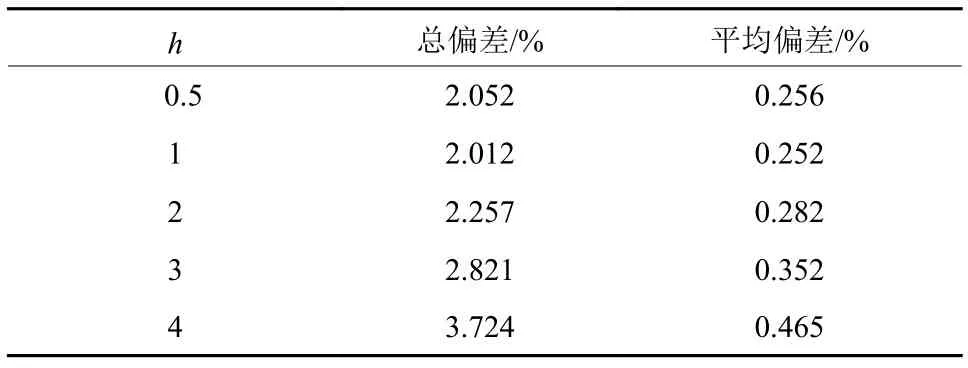
表7 偏差值表Tab.7 The deviation value

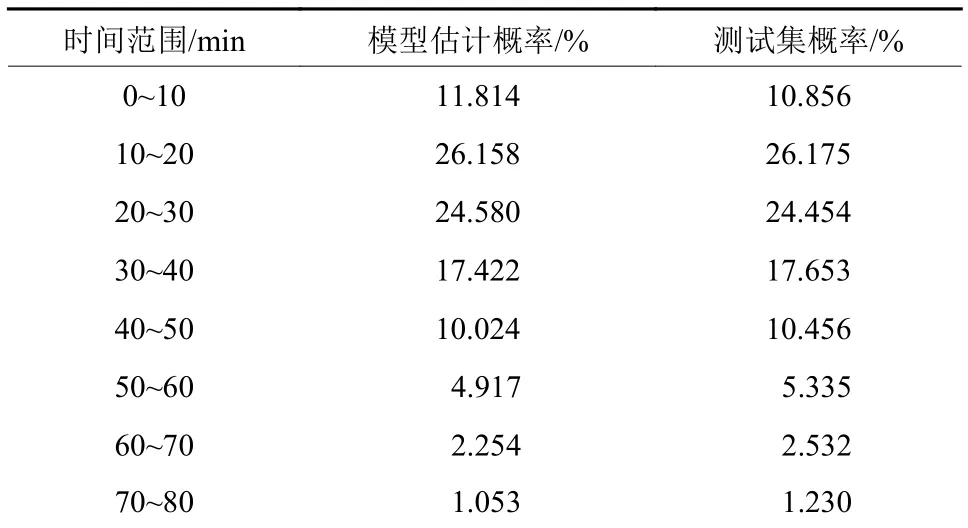
表8 模型估计的概率与实际概率对比表Tab.8 Model estimation probability and actual probability

计算可得模型估计概率与测试集概率的总偏差为2.638%，平均偏差为0.353%，说明模型泛化能力良好，能够客观、准确地反映广州居民出行时间成本的现实常态.3.2.4 模型分析

通过对出行时间范围进行加权平均(权数为概率)，可得到居民出行平均时间成本约为26.227 min，对于广州大部分居民来说，在工作日的工作时间一般为8 min，睡眠时间大概为8 h，饮食等生理活动时间大概为1.5 h，那么一天剩余的大概时间为6.5 h；非工作日(周末)的睡眠时间大概为8 h，饮食等生理活动时间大概为1.5 h，则每日大概剩余时间为14.5 h.

以每月30天，工作日22天进行计算，可以计算得到居民每天加权剩余时间均值TM为：

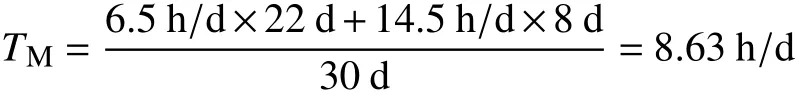
居民平均出行时间成本占剩余时间的比例为(以每

天出行2次计)：

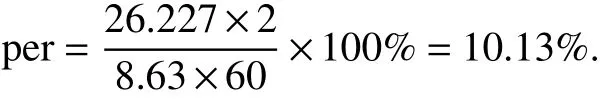
这是一个可以接受的比例，且公共交通出行时间成本在2 h以内是最合理的，当出行时间超过2 h，说明交通出行环境较差，需要政府加大公共交通治理力度，提升公共交通接驳，解决拥堵问题，提升出行体验. 根据模型输出的核密度曲线可以看出：居民公共交通出行时间成本大部分在80 min以内，且计算得到居民出行平均时间成本约为26.227 min，符合合理的公共交通出行时间成本范围，说明广州市居民出行时间成本合理.

4 结论

解决城市交通拥堵，公共交通是重要的可行方式. 在解决城市交通拥堵的同时也应考虑降低居民出行的支出成本与时间成本，以此提高居民出行的幸福指数.

本文从时间成本和支出成本两个方面，对广州IC卡数据进行核密度估计，通过对不同带宽的选取与评估，得到相对合理的带宽，最终对模型的泛化能力进行评估，算得支出成本分析的平均偏差为3.658%、时间成本分析的平均偏差为0.353%，这是一个合理的偏差范围，证明模型的泛化能力良好，适用于居民出行成本的评估分析.

本文经过建模分析，最终得到广州市居民出行成本大体是合理的，大部分广州市居民出行幸福，但是对于收入为最低工资标准的人群来说，广州市的公交收费仍然不够友好，需要加大对该人群的补助.