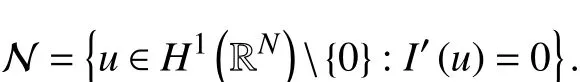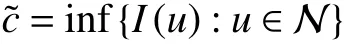全空间ℝN上的渐近线性Schrödinger方程

朱亚杰，朱红波

（广东工业大学 应用数学学院，广东 广州 510006）

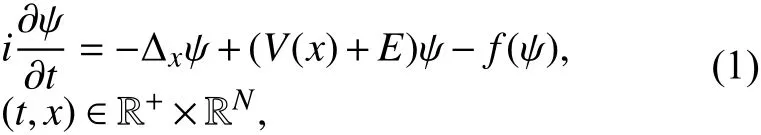
本文的研究动机来自于寻找以下非线性Schrödinger方程的驻波其中 ψ(x，t)：RN×[0，+∞)→ C，且对所有的. 方程(1)出现在许多物理应用中. 例如，在非线性光学、等离子体物理和凝聚态物理中出现的一些问题中，许多粒子的存在导致人们考虑用非线性项来模拟它们之间的相互作用.

对于方程(1)，笔者感兴趣的是寻找它的稳态解，即ψ(x，t)=u(x)eiωt，其中u (x)＞0,ω ＞0(频率)，易推导出函数u (x)满足下列方程

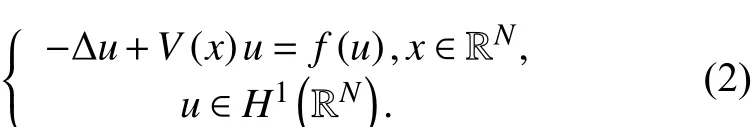
在本文中，将讨论如下带有一般非线性项的非线性方程

当位势函数 V(x)是一个常数或当| x|→ ∞时极限存在，非线性项 f(x，t)关于t在无穷远处渐近线性时，关于方程(3)存在性和多解性结论有很多，具体可见文献[1-7]. 但是在这些文献中， f(x，t)关于t在原点超线性，即当 t→0时， f(x，t)→ 0，并且q (x)是一个常数或f(x，t)≡ f(t). 本文的结果推广了文献[8]中的部分结论，在文献[8]中位势 V(x)=λ ＞0, f (x，t)关于 x是径向对称，即 f(x，t)=f(|x|，t)，并且当t ≥0时， f(|x|，t)单调非减，这两个条件的假设对文献[8]中结论的证明都起着至关重要的作用.

本文的结构如下. 在第1节中，类似于文献[8]，定义：

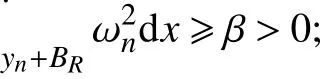
(消失)对所有的R ＞0，

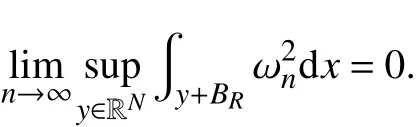
本文证明了这两种情况都不可能发生，这样就导出矛盾. 最后，文证明了有界序列收敛到能量泛函I的非平凡的临界点. 通常有两种方法可以得到这种收敛性. 一种是要证明方程(3)对应的能量泛函与该方程在无穷远的方程的能量泛函之间存在严格的大小关系. 但是，这种方法通常要求在 f(x，t)关于t 是单调非减；另一种方法是利用伸缩变换t →u(x/t)，这种方法通常处理自治问题有效，而对于本文中的非自治情况，这种处理技巧在这里不起作用.

为了避免证明过程中使用集中紧致原理的技术性的麻烦，受到文献[9-10]的启发，本文采用了一种较简单清晰的方法证明了有界序列{ un}的收敛性.

在本文中，假设 f，V 满足下列条件：

(V1)并且对所有的，

(V2)，并且对所有的

(F1)f(x，t)∈并且存在0≤ p(x)≤，使得一致成立.

(F2)对任意的

(F3)对所有的使得

主要结果如下:

设p，q满足

其中

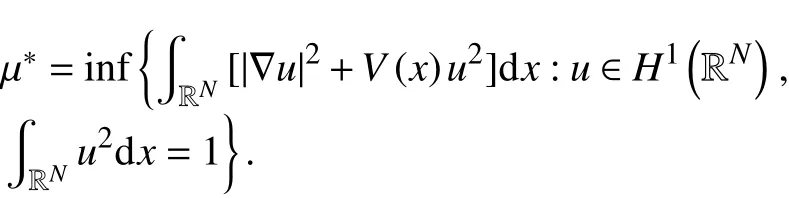
记号：在本文中，字母C 和Ci表示正常数.

BR(y)是球

1 变分泛函的性质

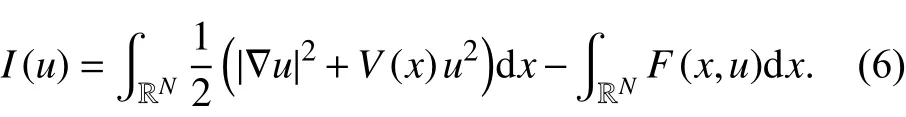
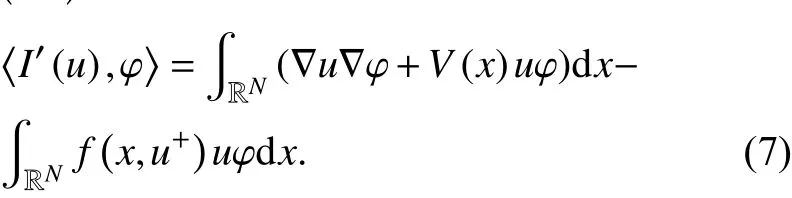
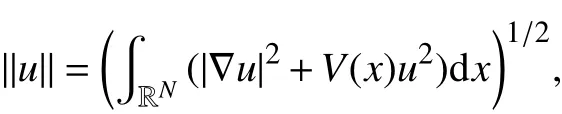
由( V1)和 (V2)可知的标准范数等价. 在条件( F1)和( F2)下，可以证明 I满足山路几何条件.

引理1 设 E 是一个实的Banach空间， E∗是其对偶空间，

满足

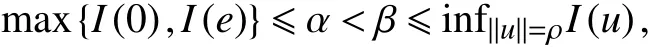
这里

引理1的证明可参见文献[11]或[12]中的第4章.带有式(8)的这种序列通常叫做临界值处的序列，简记为. 显然序列也是通常的序列.

为了应用上述山路定理，下述引理中等价范数的引入是有必要的.

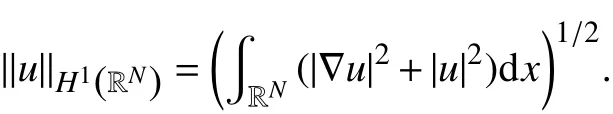
定义

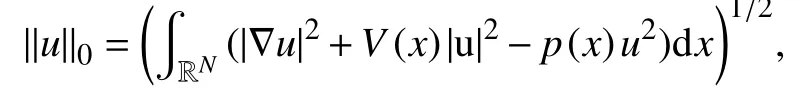
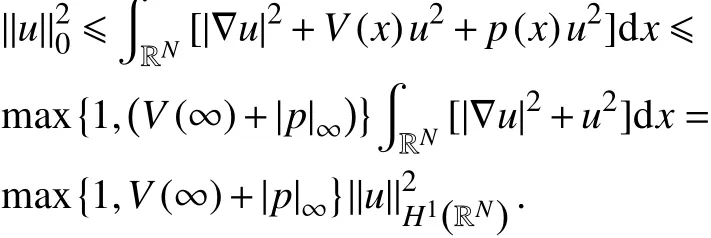
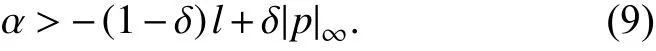
这里由式(9)可知，

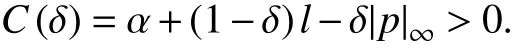
这就意味着

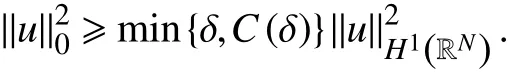
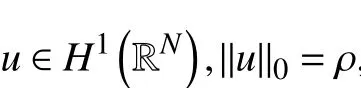
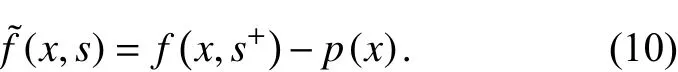
证明 为了证明这个引理，结合文献[6, 13]中的的一些想法. 令由可知关于一致成立. 由式(10)，存在使得对所有的，，

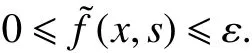
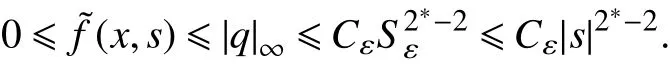
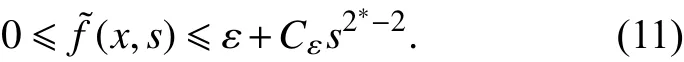
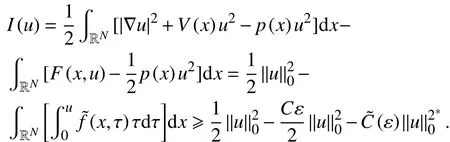
证明 这个引理的证明与文献[13]中引理4.2的证明类似. 为了完整起见，本文在这里给出了完整的证明.

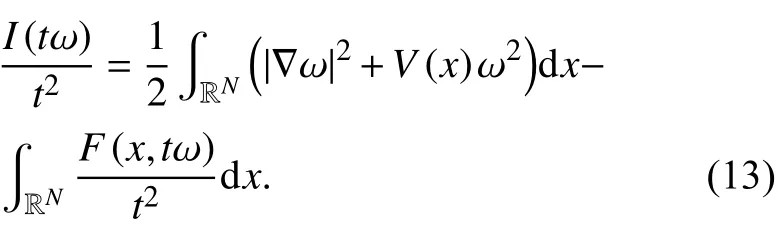
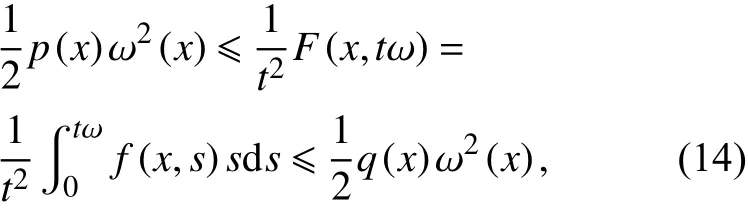
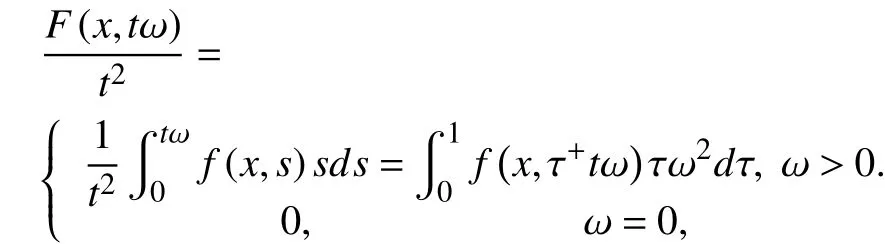
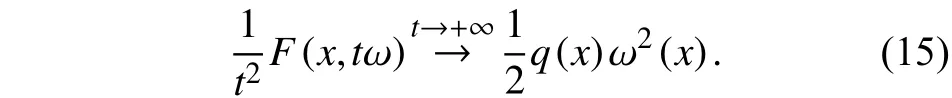
这样，由式(14—15)和控制收敛定理，

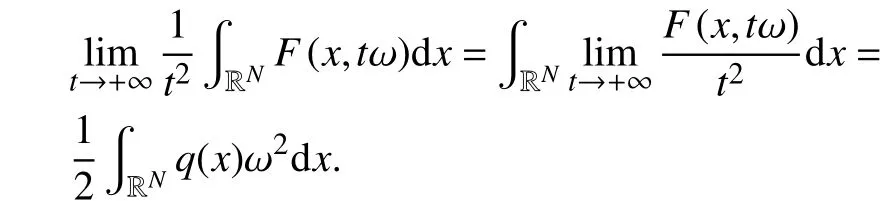
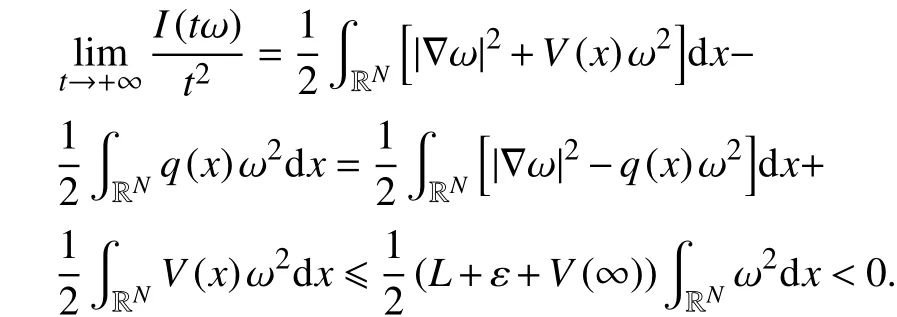
所(以，当时，，那么存在，使得.

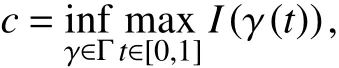
其中

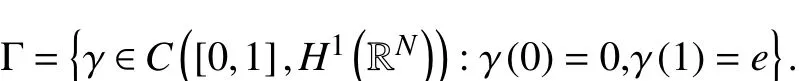
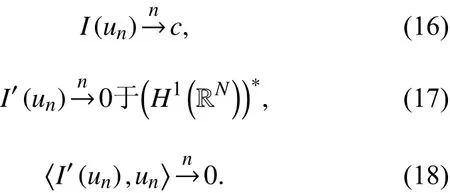
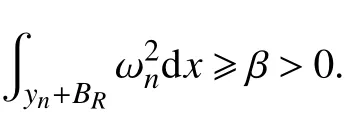
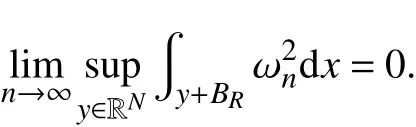
证明这两种情况都不可能发生.

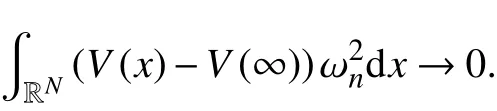
这样

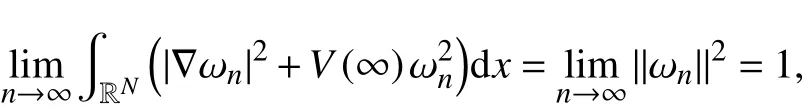
特别地，

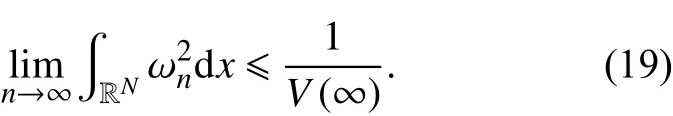
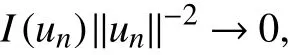
于是

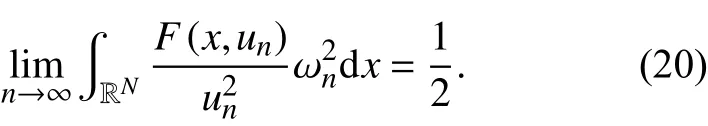
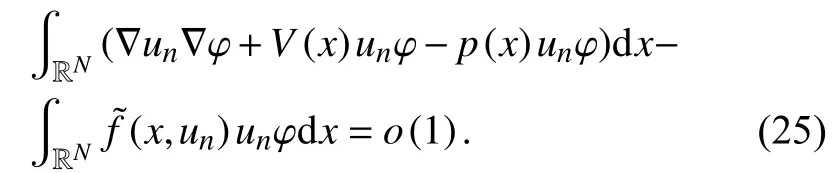
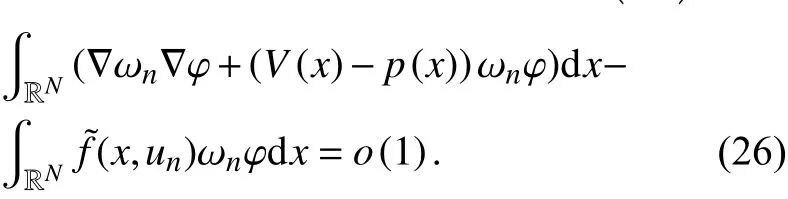
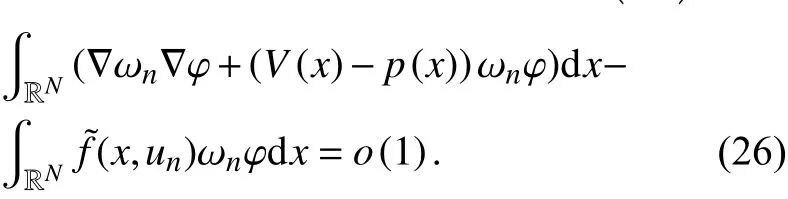
由式(21)和式(26)，有

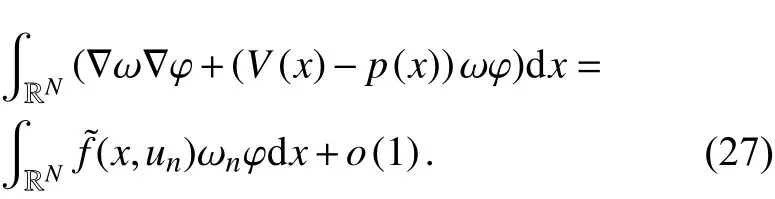
因为

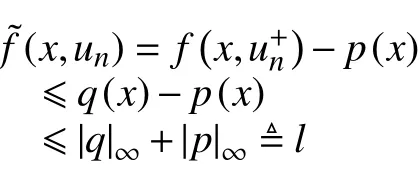
由式(21)～(23)可知，对所有的φ ∈C0∞，

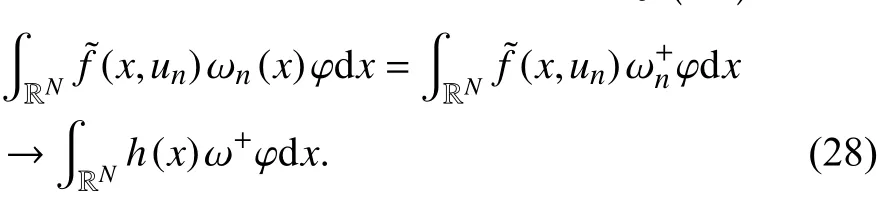
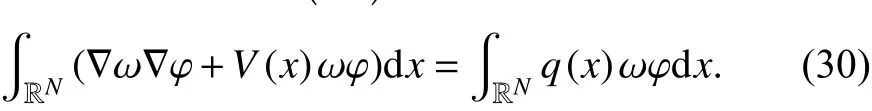
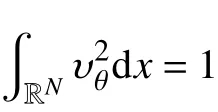
且

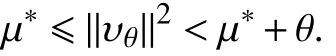
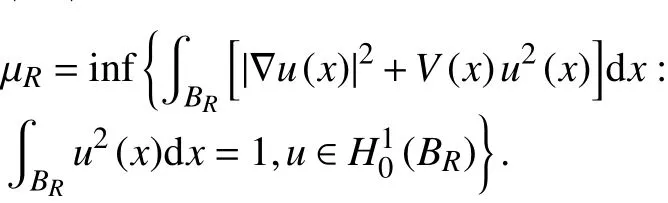
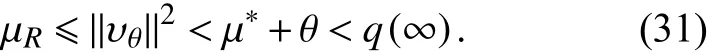
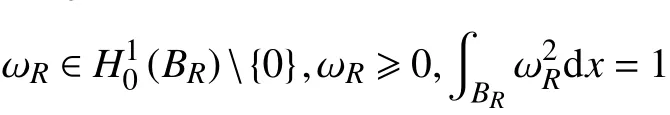
使得

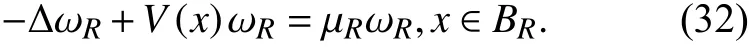
由强极值原理可得

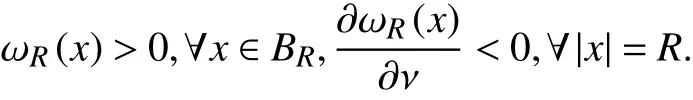
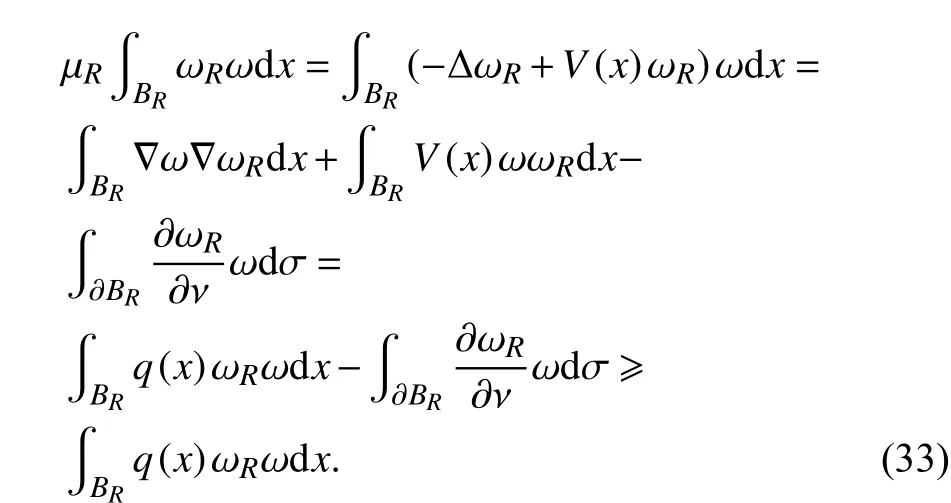
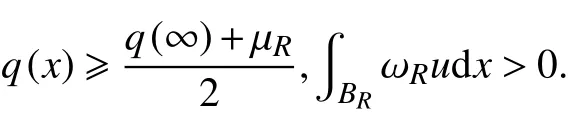
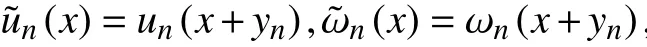
而且，

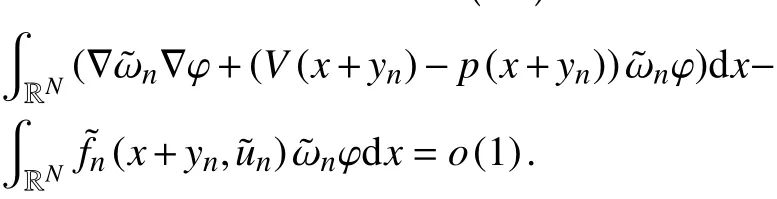
显然，

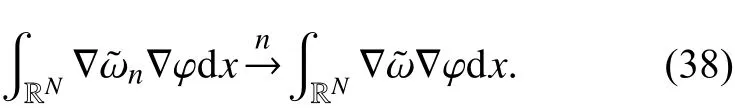
接下来，证明

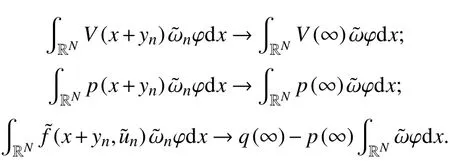
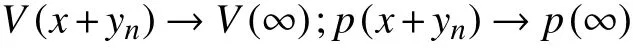
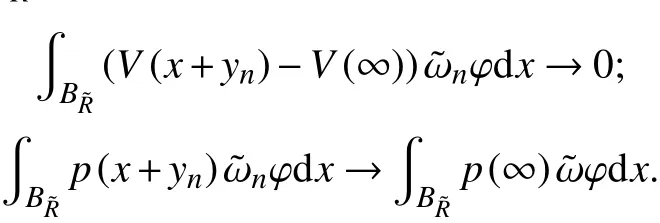
因此，

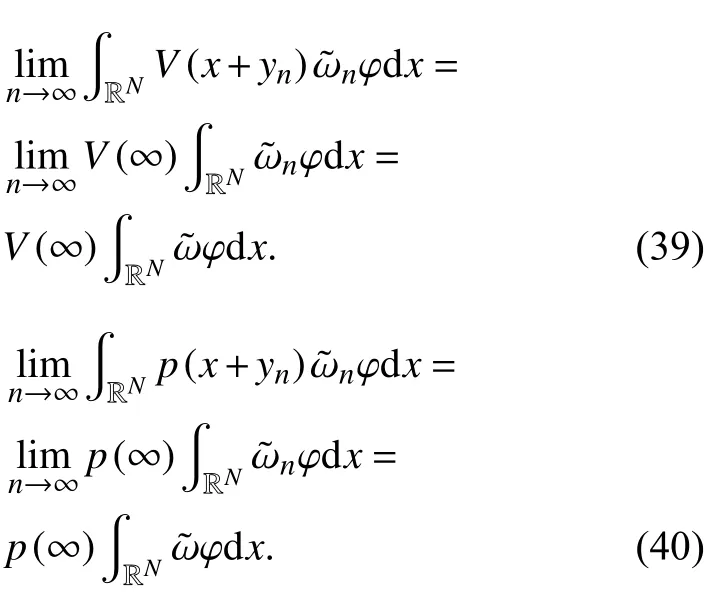
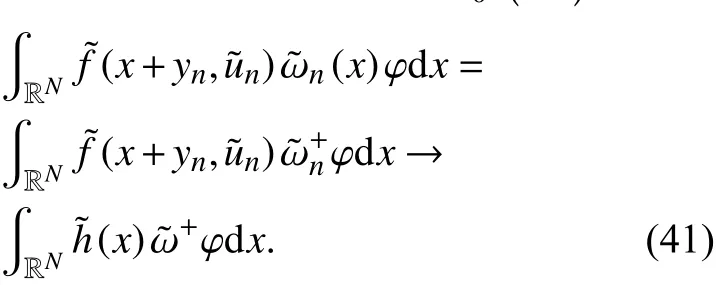
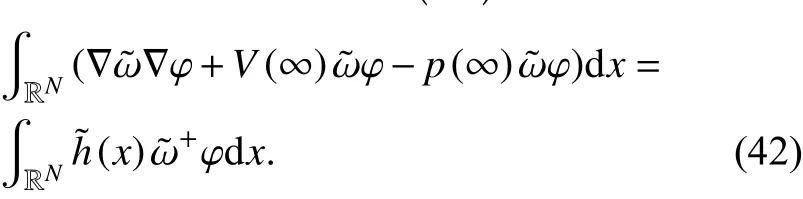
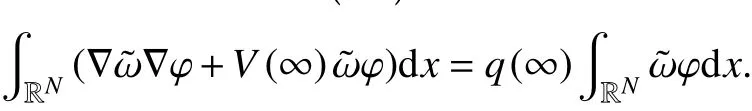
3 主要结果的证明

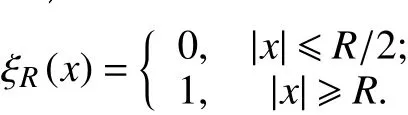
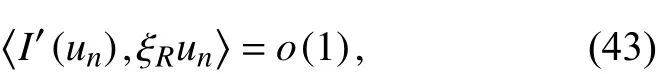
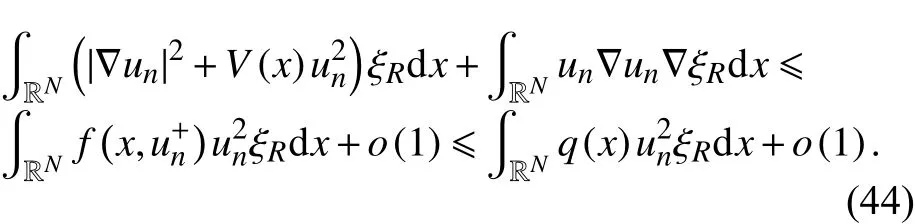
因为

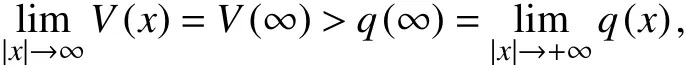
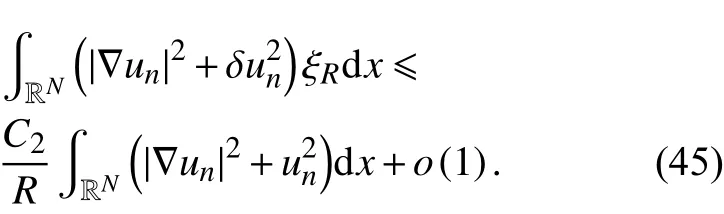
这样，

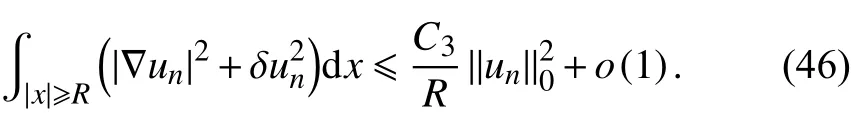
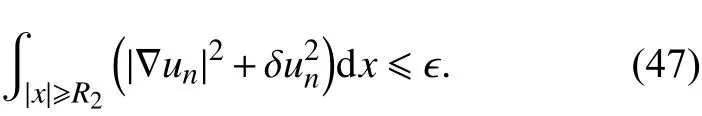
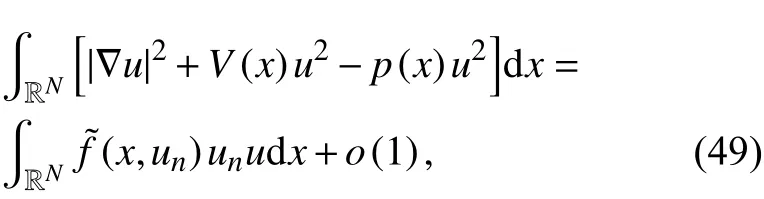
且

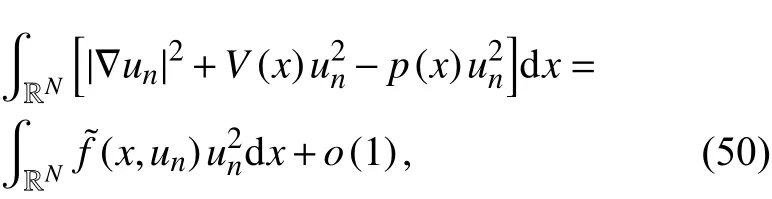
因此，

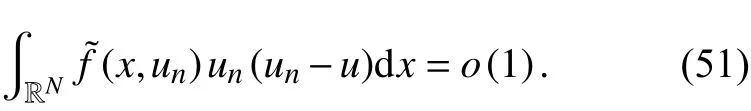
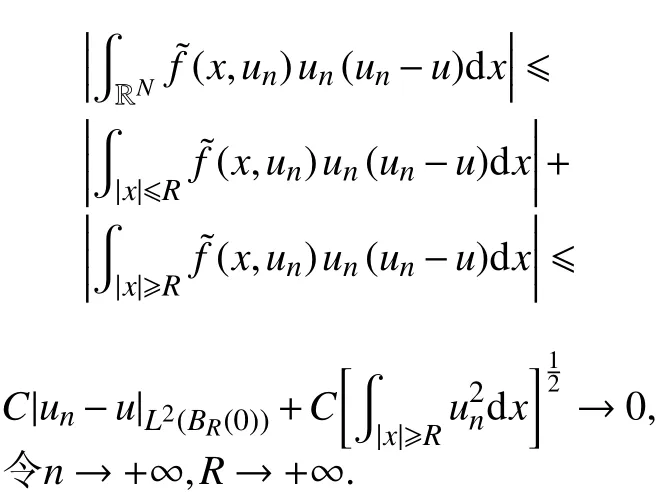
因此，式(51)得证.

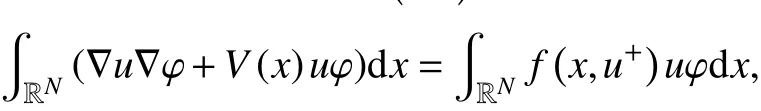
即

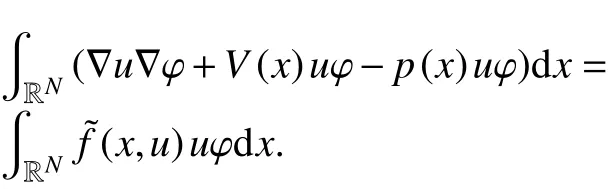
取φ =u-=min{0，u}，可以看出

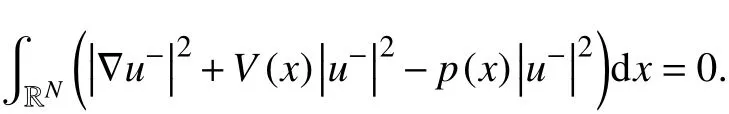
证明定理2 令