水压力和地震作用下岩质边坡倾覆破坏稳定性研究

柯 鉴，邓 琴，梁栋才,3，段文正，李 睿

(1. 西双版纳景海高速公路建设投资有限公司，云南 景洪 666100；2.中国科学院武汉岩土力学研究所岩土力学与工程国家重点试验室，武汉 430071；3. 中国科学院大学，北京 100000；4. 云南大永高速公路有限公司，云南 大理 671000)

0 引 言

随着国家“一带一路”和长江经济带的战略实施，水利和交通建设迅猛发展，沿线地区的地质条件异常复杂，岩质边坡稳定性问题日益获得人们关注，成为一个急需解决的重大课题[1-4]。岩质边坡的失稳模式根据岩性的不同有所差异，其中硬质岩坡主要是由显著结构面控制，破坏形态有平面破坏、楔形破坏和倾倒破坏[5,6]。目前关于平面破坏，主要是考虑沿着结构面的顺层滑移破坏[7-11]，这是基于外界荷载作用线通过滑体重心，仅考虑力平衡的假定得到的。许光详[12]指出，地下水的存在使得岩质边坡的倾覆破坏成为可能，这是由于地下水对边坡产生的静水压力对边坡产生绕坡脚的倾覆力矩。在此基础上，众多学者开展了抗倾覆稳定性分析，并开展了几何参数和影响因素的敏感性分析[6-19]。然而，上述研究中关于水压力分布的形式在某些状态下并不合理。李伟[20]全面分析了Hoek[5]和舒继森[19]水压力分布存在的一些缺陷，提出结构面上的静水压力分布是初始静水压力和传递效应共同作用的结果，建议了改进的水压力分布形式，并进行了极值分析和已有公式的对比分析，结果说明，新公式具有较好的合理性。李伟[21]和邵光钦[22]在此合理的水压力分布基础上分别开展了平面滑动破坏的极限解析解和顺层滑动边坡的破坏研究。

上述学者大多研究的是边坡在静水压力、水压与地震联合作用和极端灾害天气下的倾覆分析，鲜有学者研究外界荷载(水压力、地震和坡顶荷载)联合作用下的边坡倾覆稳定性分析。除了地震和水压力以外，坡顶荷载是水利工程边坡、铁路边坡以及公路边坡等稳定性分析中不可忽略的因素[23]。因此，基于合理的水压力分布形式，采用拟静力法，考虑静水压力、地震荷载和坡顶荷载的联合作用，推导出岩质边坡在外界荷载综合作用下的抗倾覆安全系数表达式，并深入探讨影响因素对倾覆稳定性的影响，对该类边坡设计施工具有重要的工程意义。

1 外界荷载作用下岩质边坡的受力分析及倾覆稳定性系数计算

1.1 计算模型

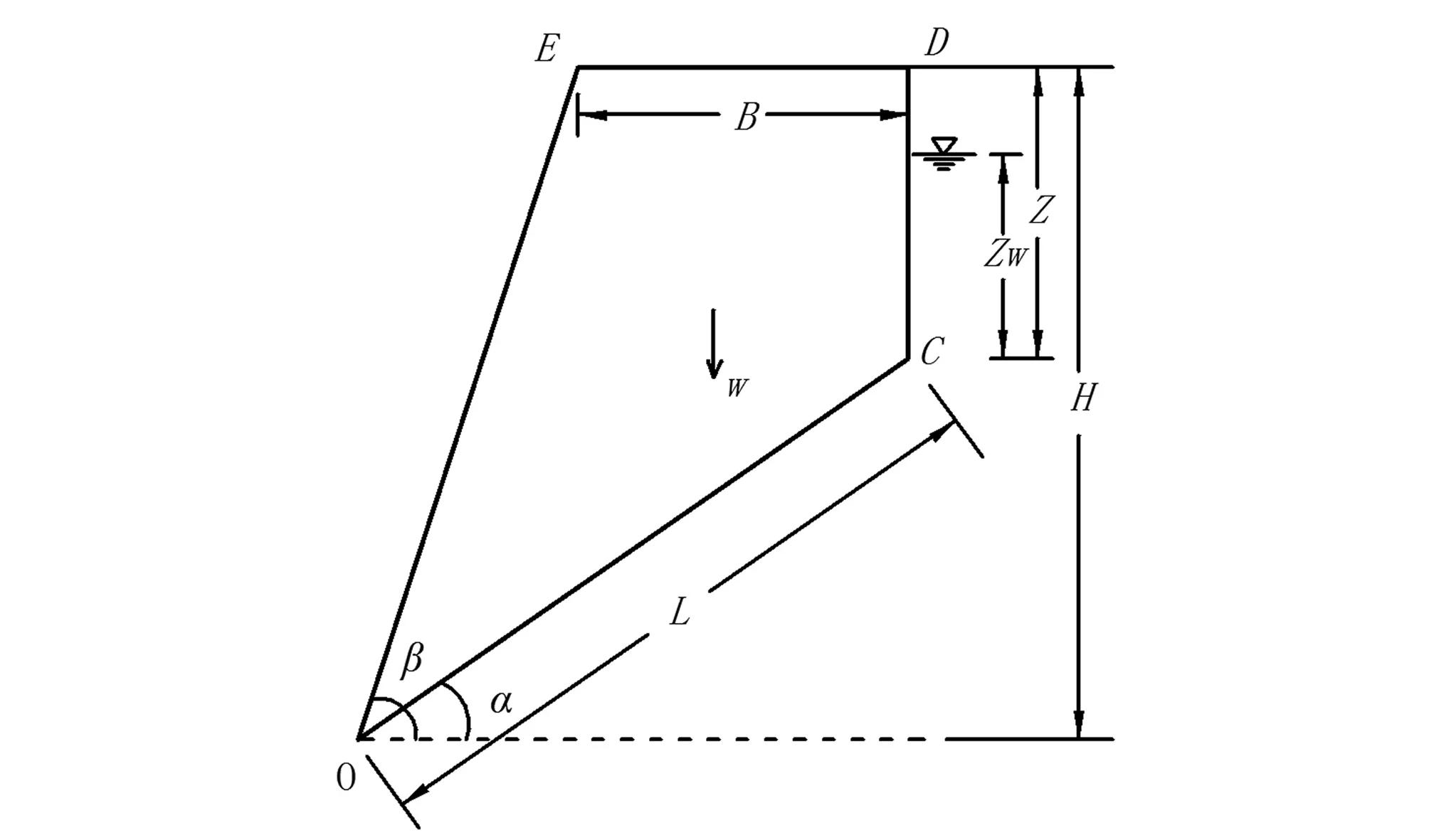
图1 典型岩质边坡几何要素Fig.1 Geometric factors of typical rock slope

1.2 受力分析

考虑潜在倾覆体受自重、张裂缝和结构面的静水压力、地震惯性力和坡顶荷载作用，其中静水压力考虑采用李伟[17]提出的改进水压力分布形式，考虑出流缝堵塞与不堵塞两种工况，受力如图2和图3所示。

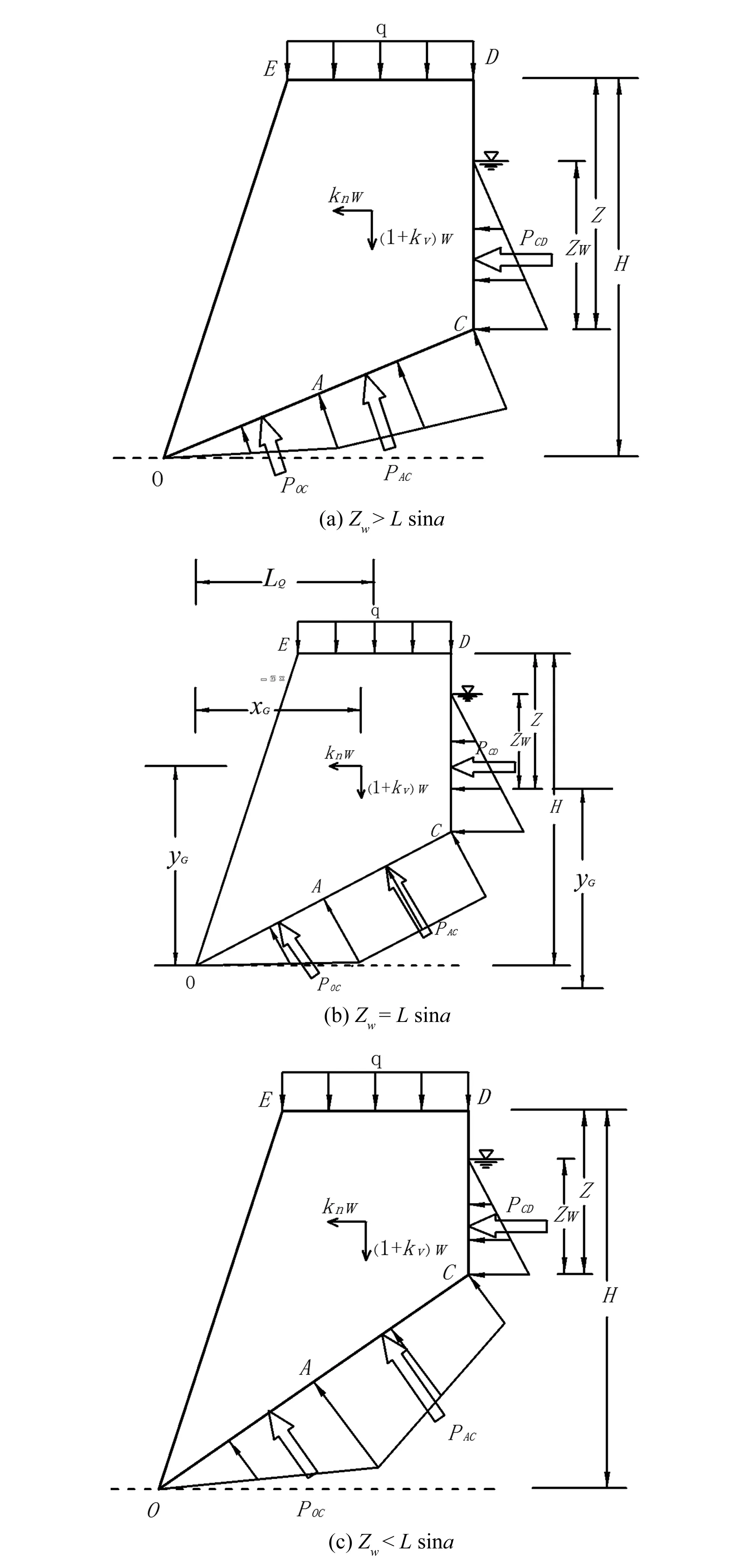
图2 出留缝不堵塞情况下倾覆体受力分析Fig.2 Forces analysis of overturning mass under outflow seam unblocking

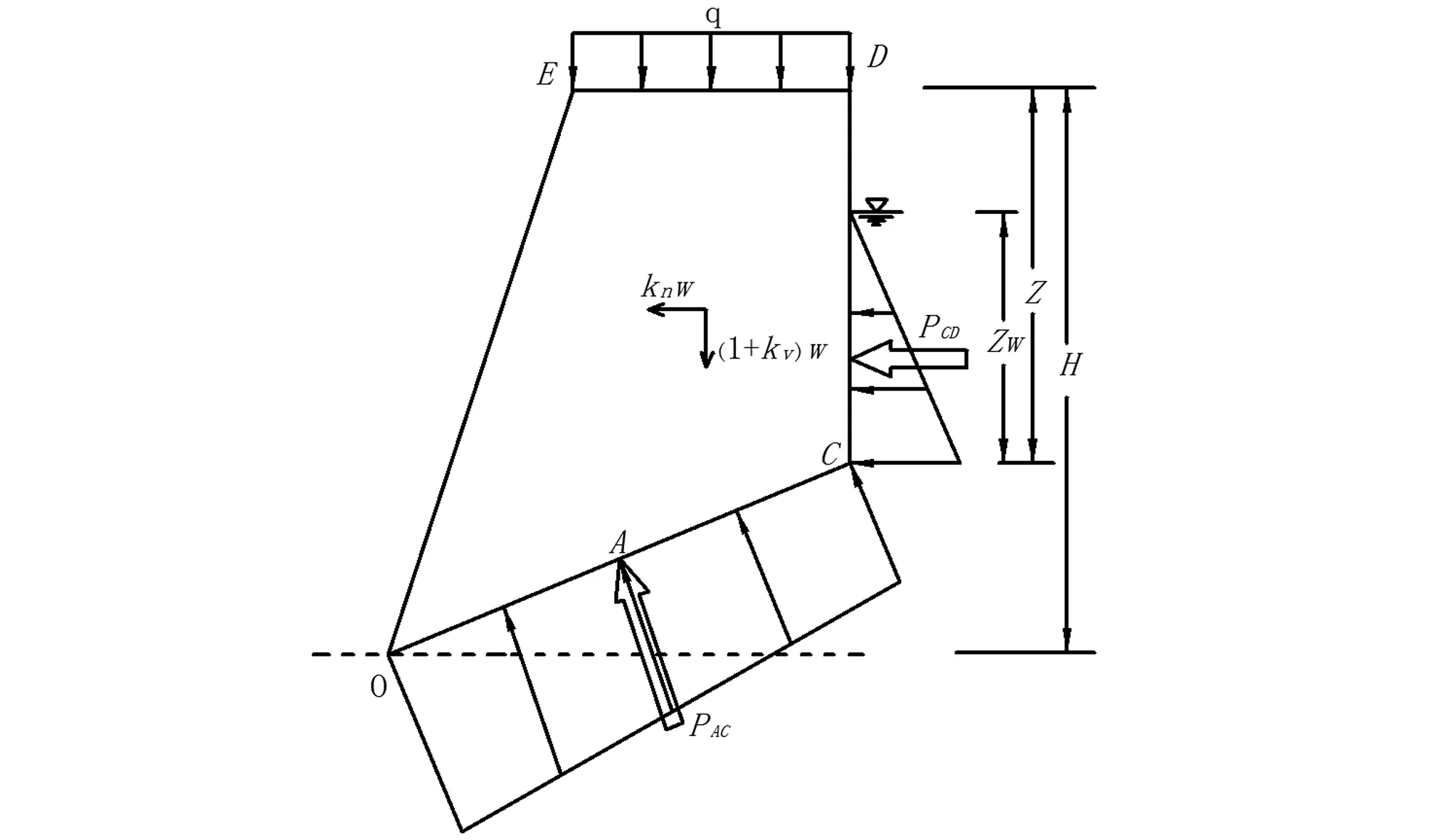
图3 出留缝堵塞情况下倾覆体受力分析Fig.3 Forces analysis of overturning mass under outflow seam blocking

(1)重力和地震力的计算。假设坡体重度为天然重度γ，不考虑水对其重度的影响，则重力为：

(1)

重心距离坡趾O的水平距离xG和竖直距离yG分别为：

(2)

(3)

地震力等效为作用在潜在滑体上重心的两个静态力，分别为水平作用力khW和竖直方向力kvW，且kv=ζkh。其中kh、kv分别代表水平和竖直方向的地震作用系数，ζ为比例系数。根据文献[16,18]关于地震系数的取值范围，这里kh取值范围为0～0.6，ζ取值范围为-1.0～1.0，且负值表示竖直作用力向下。

(2)坡顶荷载的计算。其中坡顶荷载假定以均布形式分布，大小为q。则坡顶荷载的合力及其绕坡趾O力臂为：

Q=qB=q[(H-Z)cotα-Hcotβ]

(4)

(5)

(3)静水压力的计算。张裂缝CD上的静水压力合力及其绕坡趾O力臂为：

(6)

(7)

① 出流缝不堵塞的情况，结构面OA段的静水压力合力POA及其绕坡趾O力臂为：

(8)

(9)

结构面AC段的静水压力合力PAC及其绕坡趾O力臂分别为：

(10)

(11)

② 出流缝堵塞的情况，结构面OC段的静水压力POC及其绕坡趾O力臂为:

(12)

(13)

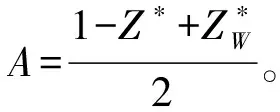
1.3 抗倾覆稳定性系数计算

考虑最危险的倾覆破坏为绕坡脚(即O点)的倾覆破坏。绕坡脚的抗倾覆力矩MR与倾覆力矩分别为：

(14)

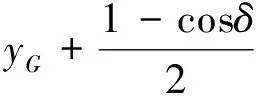
(15)

其中出流缝堵塞时，MOC=POCLOC；出流缝未堵塞时，MOC=POA·LOA+PAC·LAC。

因此，考虑外界荷载作用时，绕坡脚(即O点)的抗倾覆稳定系数为：

(16)

其中：

S1=(1+2Z*) (1-Z*)2cot2α-cot2β

(17)

S2=(1-Z*)2cot2α-cot2β

(18)

S3=(1-Z*)[3-(1-Z*)2]cotα-2 cotβ

(19)

(20)

(21)

当kv≥0时，δ1=1，δ2=0；当kv<0时，δ1=0，δ2=1。

2 水压力分布形式合理性分析

分析比较Hoek E提出的原始水压力分布[5]，舒继森改进的水压力[19]和本文采用的李伟提出的水压力分布[20]可以发现其中的差异：

(1) Hoek E提出的原始水压力分布形式在张裂缝的底部静水压力最大。当张裂缝内无水时，张裂缝底部水压力为0，相应的结构面上水压为0，对边坡倾覆稳定系数不产生影响，即F保持不变，这明显不符合工程实际。

(2) 舒继森在原始水压力分布的基础上，假定地下水位1/2处静水压力最大，为(Lsin(α)+Zw)/2。当ZwH-Z时，c点静水压力为γw(H-Z)。根据水力学理论[21]，张拉裂隙上的静水压力与水头高度始终呈线性分布关系。显然，舒继森模型在Zw>H-Z时的张裂缝的静水压力分布存在不足。

(3)李伟等提出结构面上的静水压力由初始静水压力和传递效应共同作用的结果，其水压力分布如图2所示。通过极值条件分析水压力分布[20]，其结果与传统水力学结果一致。因此，新的水压力分布具有较好的合理性。

为分析上述边坡水压力分布形式对岩质边坡倾覆稳定系数的影响，选取基本边坡的参数如下：坡高H=20 m，坡角β=60°，倾角α= 40°，竖向裂缝高度Z=8 m，rw/r=2.5，rw=25 kN/m3，q=0～500 kN/m，水平地震系数kh=0～0.6。竖向裂缝饱水状态下，考虑q=500 kN/m，kv=-0.3，边坡抗倾覆稳定系数的变化如图4所示。

图4 不同水压力分布形式下倾覆稳定性系数F与水平地震系数Kh的关系曲线Fig.4 Relation between coefficient of overturning stability and horizontal earthquake under different water pressure distribution

从图4中可以看出，①无论采用哪种水压力分布形式，在其他条件相同时，边坡的抗倾覆稳定系数F随着水平地震系数的增加而明显减小。如3种水压力分布形式下，kh=0.6时的稳定性系数比不考虑地震时的稳定性系数分别降低了51.2%、45.5%和43.3%。这是由于随着水平地震系数的增加，水平地震力引起的倾覆力矩变大，从而导致稳定性系数减小。②相同参数影响下，本文采用的水压力分布假设得到的倾覆稳定性系数比Hoek E和舒继森水压力分布形式计算的结果要小。如kh=0.3时的抗倾覆稳定系数F分别为2.03，1.74和1.63。文献[19]和[20]详细分析了Hoek E和舒继森水压力分布假设在一些极限情况下存在的不足，并针对几何要素开展了敏感性分析，证实了本文采用的水压力分析形式具有较好的合理性。

综上，后续采用文献[20]提出的合理的水压力分布形式进行研究。

3 影响因素的研究

(1)地震的影响。在上述基本边坡中，取kv=ζkh，kh取值范围为0～0.6，ζ取值范围为-1.0～1.0。

考虑出流缝未堵塞与堵塞工况，不同地震系数比下边坡的抗倾覆稳定系数F与水平地震系数的关系。计算结果如图5所示。从图5中可以看出：①无论出流缝是否堵塞，倾覆稳定系数F均随着水平地震力的增加而逐渐减小。这是由于水平地震力的增加，使得边坡的倾覆力矩增大，从而导致稳定系数减小。②其他条件相同时，出流缝未堵塞下边坡的倾覆稳定性系数比堵塞情况下的结果要大。从公式(22)看出，出流缝堵塞时的Moc比未堵塞时的大，导致倾覆力矩比未堵塞时的小，从而导致未堵塞边坡的倾覆稳定性系数相对大一些。③其他条件相同时，当竖向地震指向由竖直向下转向竖直向上时，边坡的倾覆稳定性系数F逐渐减小。这是由于竖向地震逐渐减小，其产生的力矩从抗倾覆变成了倾覆的缘故。

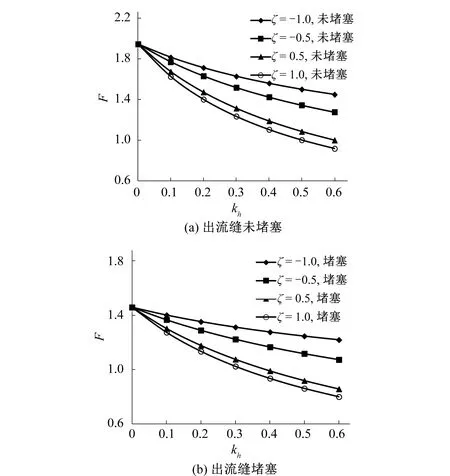
图5 不同地震作用系数比下倾覆稳定性系数F与水平地震系数Kh的关系曲线Fig.5 Relation between coefficient of overturning stability and horizontal earthquake under different ratio of earthquake action coefficient

(2)张裂缝积水深度的影响。考虑出流缝未堵塞与堵塞工况，不同裂隙水深度下边坡的抗倾覆稳定系数F与水平地震系数的关系。计算结果如图6所示。从图6中可以看出：①无论裂隙水是否充满裂缝，边坡抗倾覆稳定系数F均随着水平地震力的增加而逐渐减小。这是由于水平地震力的增加，使得边坡的倾覆力矩增大，从而导致稳定系数减小。②其他条件相同时，当裂隙水深度降低时，边坡抗倾覆稳定系数F逐渐增加。这是由于裂隙水深度减小，竖向裂缝内水压力引起的抗倾覆力矩减小，从而导致抗倾覆稳定系数增加。这和许光祥[9]提出的饱水边坡更易发生倾覆一致。

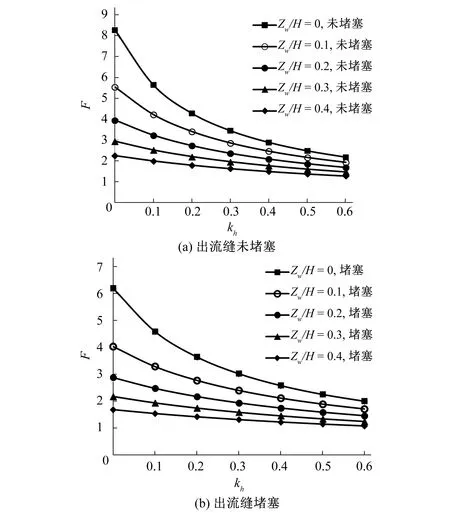
图6 裂隙水不同深度下倾覆稳定性系数F与水平地震系数Kh的关系曲线Fig.6 Relation between coefficient of overturning stability and horizontal earthquake under different depths of fissure water

(3)坡顶荷载的影响。考虑出流缝未堵塞与堵塞工况，坡顶不同荷载下边坡的抗倾覆稳定系数F与水平地震系数kh的关系。计算结果如图7所示。从图7中可以看出：①无论坡顶荷载大小，边坡抗倾覆稳定系数F均随着水平地震力的增加而逐渐减小。这是由于水平地震力的增加，使得边坡的倾覆力矩增大，从而导致稳定系数减小。②其他条件相同时，当坡顶荷载增加时，边坡抗倾覆稳定系数F逐渐增大。这是由于随着坡顶荷载的增加，堆载引起的抗倾覆力矩变大，从而导致抗倾覆稳定系数提高。

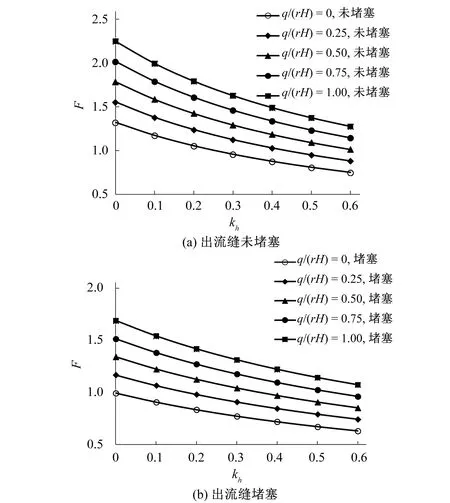
图7 不同坡顶荷载下倾覆稳定性系数F与水平地震系数Kh的关系曲线Fig.7 Relation between coefficient of overturning stability and horizontal earthquake under different load of the top of slope

4 结论与建议

采用李伟等提出的合理的水压力分布形式，基于力矩平衡原理，开展了岩质边坡在外界荷载(包括地震、水压力和坡顶荷载)作用下的抗倾覆稳定性分析，得出了无量纲的倾覆稳定系数表达式，得出以下结论：

(1) 新提出的水压力分布形式(结构面中点和张裂缝底部水压力是定值)克服了原始水压力分布形式(竖直张裂缝底部静水压力最大)和改进水压力分布形式(地下水位1/2 处静水压力最大)的不足，其抗倾覆稳定系数比其他两种方法均小，且更合理。

(2) 出流缝堵塞时，边坡倾覆稳定性系数显著降低。这是由于出流缝堵塞后，结构面水压力产生的力矩大于未堵塞时的力矩；抗倾覆稳定系数随着水平地震力的增加逐渐减小。当水平地震力保持不变，稳定系数随着地震作用系数的增加逐渐减小；边坡抗倾覆稳定系数随着裂隙水深度的降低而减小，饱水状态下边坡的倾覆稳定系数最小。坡顶荷载的增加有利于边坡的稳定。

□