黄河兰州段水质评价的HDE方法应用

逯晔坤，靳春玲，贡 力

(兰州交通大学土木工程学院，兰州 730070)

0 引 言

水是地球表面最多的天然物质，覆盖了71%以上的表面。作为生活不可缺少的重要组成部分，水质的好坏对人类生活具有深远的影响。近年来，随着基础工程的大量建设，相关产业产生了大量工业废水并没有合理处置，导致一些生态环境被破坏，水的自净功能降低，使水质发生恶化，严重影响了人类正常生活，保护水资源，防治水污染已成为重要一环。黄河自西向东流经9个省及自治区，提供了丰富的水资源。兰州作为黄河唯一穿城而过的省会城市，黄河水的使用作为城市用水的主要来源，使得对水质的要求变得尤为突出，故而对黄河兰州段水质进行评价，对兰州经济和社会的可持续发展具有重要的现实意义。

国外水质评价始于20世纪60年代中期，在70年代发展较为繁荣，各种评价水质质量指数的方法被相继提出，20世纪80年代，国内学者对水质质量指数计算进行了改进，提出了几何均数评价[1]、半集均方差评价[2]等。随着发展水质评价产生大量评价方法，但没有确定、统一的评价方法，国内外对水质评价的研究方法主要分为单因子评价法、综合指数评价法和综合评价方法(包括：模糊综合评价法、主成分分析法、集对分析法、灰色评价法及人工神经网络法等)[3-8]。单因子评价法是以最差因素的水质级别作为最终水质评价级别，评价结果保守；综合指数评价法方便易用，但没有考虑因素的权重；综合评价方法考虑影响水质的多个指标与评价标准的关系，从而确定水质的综合结果[9]。

在和谐理念下，采用和谐理论定量分析方法—和谐度方程(HDE)，考虑影响水质因素的和谐程度，建立新的评价模型。马军霞[10]利用和谐度方程的“分类等级评价”方法对水质进行了评价，本文在参考其基础上利用和谐度方程“综合程度评价”方法[11]对黄河兰州段水质进行评价。

1 和谐度方程(HDE)评价模型

左其亭教授于2009年在《和谐论的数学描述方法与应用》中把研究“和谐”行为的理论和方法体系称为和谐论(harmony theory)，并进一步定义“和谐论是研究多方参与者共同实现和谐行为的理论和方法”[12,13]。和谐论具有广泛的应用前景，是揭示自然界和谐关系的重要理论，其定量表达方法为和谐度方程(harmony degree equation)，被期刊《The Scientific Word Journal》编辑称为“左氏和谐度方程”(Zuo-harmony degree equation)[14]。自和谐度方程提出以来，在水资源的研究中做出了一定的成果，比如跨界河流分水问题[15]；流域人水和谐问题[16]；入河污染物排放量分配问题[17]；水资源分配和调度优化问题[18]。

1.1 和谐度方程表达式

1.1.1 单因素和谐度方程

HDk=ai-bj

(1)

式中：HDk为某一因素Fk对应的和谐度，是表达和谐程度的指标，HDk∈[-1，1]；a为统一度(unity degree)，和谐参与者按照和谐规则具有“相同目标”所占的比重，a∈[0，1]；b为分歧度(difference degree)，和谐参与者对照和谐规则和目标存在分歧情况所占的比重，b∈[0，1]；i为和谐系数(harmony coefficient)，反映和谐目标的满足程度，可依据和谐目标计算确定，i∈[0，1]；j为不和谐系数(disharmony coefficient)，反映和谐参与者对存在分歧现象的重视程度，可以根据分歧度计算确定，j∈[0，1]。

1.1.2 多因素和谐度方程

(1)加权平均计算。

(2)

式中：HD为综合和谐度，HD∈[-1，1]；wk为权重，wk∈[0，1]。

(2)指数权重加权计算。

(3)

式中：βk为指数权重，βk∈[0，1] 。

1.2 和谐度方程各参数确定方法

(1)统一度a。

a=φ(A1，A2)

(4)

式中：φ(A1，A2)为和谐行为A1与A2之间的关联程度隶属度，通常对指标体系建立线性函数进行计算。

(2)分歧度b。分歧度b与统一度a表达的意思相反，且a+b=1 ，故：

b=1-φ(A1，A2)

(5)

(3)和谐系数i。根据和谐目标满足程度确定和谐系数曲线，即而确定和谐系数，本文采用和谐系数两节点公式计算，故：

(6)

(4)不和谐系数j。 其反映和谐参与者对存在分歧现象的重视程度，可以根据分歧度计算确定，一般取j=b。

因和谐度方程参数确定较为灵活，详细计算参照文献[12]。

1.3 和谐度方程评价流程

(1)确定评价指标及指标标准。

(2)确定单因素和谐度。按照指标标准，分别计算指标的统一度a、分歧度b、和谐系数i、不和谐系数j，确定指标的和谐度。

(3)确定指标的权重。

(4)确定综合和谐度。通过上述多因素和谐度计算方法，计算出评价对象的和谐度值。

(5)确定评价结果。对比评价标准确定最终结果。

图1 和谐度方程评价流程Fig.1 Harmony equation evaluation process

2 黄河兰州段水质评价

2.1 评价指标数据

以兰州环境保护局2017年黄河兰州段新城桥断面和什川桥断面黄河水pH值、水温、浊度、溶解氧、电导率、氨氮和高锰酸盐指数7项指标的自动监测数据为基础，进行黄河水质评价。具体数据见表1和表2。

2.2 评价指标等级标准

我国依据地表水水域环境功能和保护目标，将水质划分为Ⅰ～Ⅴ类，不同功能类别分别执行相应类别的标准值。按照《地表水环境质量标准》(GB 3838-2002)确定上述除浊度和电导率外5项指标的等级标准，浊度和电导率单独进行级别考虑，见表3。

2.3 评价指标和谐度参数计算

2.3.1 统一度a计算

根据表3的标准划分和相关研究，对相关指标建立线性函数，按式(4)确定指标每一季度的统一度，如下：

表1 黄河兰州段2017年水质监测数据Tab.1 Water quality monitoring data for 2017 in the Yellow River Lanzhou Section

表2 黄河兰州段2017年四个季度水质监测数据Tab.2 Water quality monitoring data for the fourth quarter of 2017 in the Yellow River Lanzhou section

表3 黄河水质评价相关指标及其标准值 mg/L

(7)

(8)

(9)

其余指标中浊度(TB)和电导率(EC)在《地表水环境质量标准》(GB 3838-2002)中没有明确要求，以黄河的实际情况考虑，取统一度a=0.5；考虑兰州的温度变化情况对水温(T)的影响情况，取统一度a=0.5；溶解氧(DO)的实测值全部高于7.5 mg/L，满足Ⅰ类水质的标准，取统一度a=1。详细计算数值见表4。

2.3.2 分歧度b计算

分歧度b表示和谐参与者对照和谐规则和目标存在分歧情况所占的比重，与统一度a表达的意思相反，故按式(5)进行计算，各指标分歧度数值见表5。

2.3.3 和谐系数i计算

根据和谐目标满足程度确定和谐系数曲线或函数。本文和谐系数计算通过模糊思想，将和谐系数按照地表水等级标准划分为0～0.25、0.25～0.5、0.5～0.75、0.75～1、1五类并和各指标具体划分范围进行匹配，按照式(6)，确定各指标和谐系数。

水温、浊度和电导率取i=0.5，溶解氧取i=1，指标详细数值见表6。

表4 各指标统一度a 值Tab.4 Unity degree “a” value of each indicator

表5 各指标分歧度b值Tab.5 Difference degree “b” value of each indicator

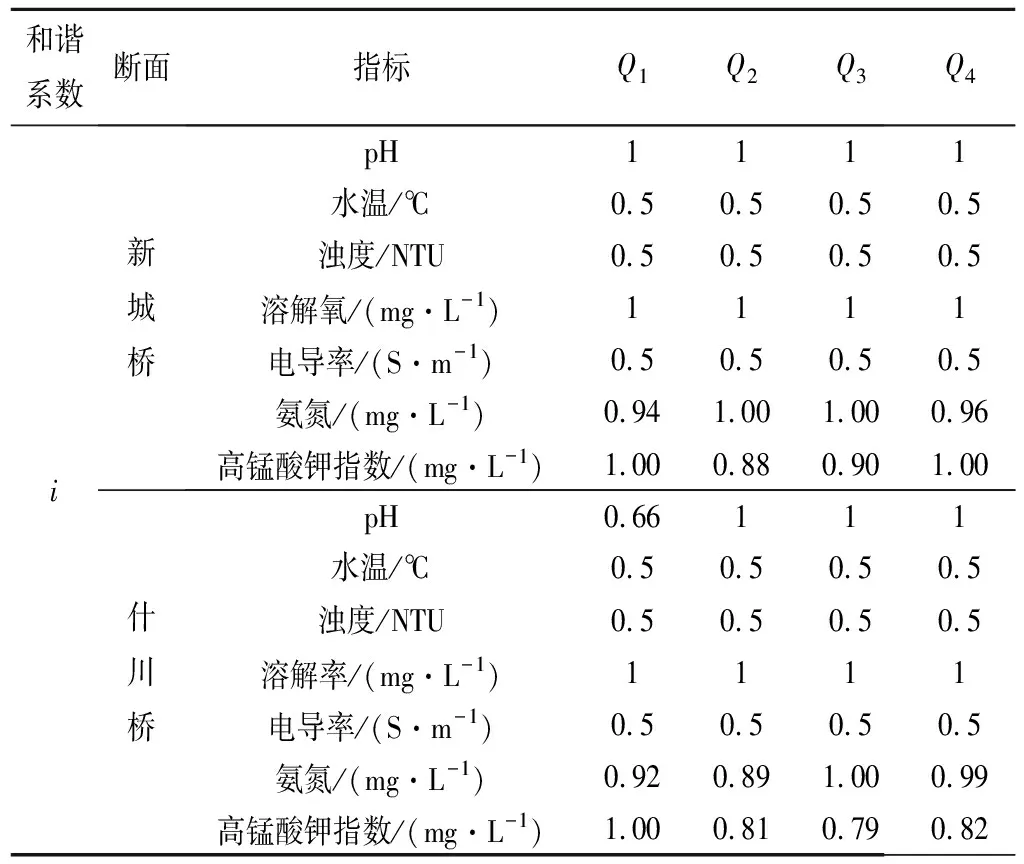
表6 各指标和谐系数i值Tab.5 Harmony coefficient “i” value of each indicator

2.3.4 不和谐系数j计算

不和谐系数j反映和谐参者对从在分歧现象的重视程度，可以根据分歧度计算确定，即j=b，各指标不和谐系数参照表5确定。

2.4 确定各指标和谐度HDk

采用式(1)确定各指标和谐度值，结果见表7。

表7 各指标和谐度值Tab.7 harmony degree values of each indicator

2.5 确定权重

(1)通过对两断面各指标的监测数据，采用熵权法确定PH值、水温、浊度、溶解氧、电导率、氨氮、高锰酸盐指数7项指标的权重值，结果见表8。

表8 各指标权重Tab.8 weights of indicators

(2)因为每季度跨度较长，无法精确确定其权重，故采用等权重法，确定每季度的权重，即每季度的权重分别为0.250；新城桥、什川桥断面分别为兰州段上游和下游的监测断面，具有同等作用，故权重分别为0.500。

通过采用等权重法和熵权法相结合的主客观方法确定权重，减少了权重的主观性，使权重更加客观。

2.6 确定兰州段黄河水质的和谐度

采用多因素和谐度方程的加权平均计算公式[式(2)]，计算各项指标每季度的和谐度，即：

(10)

式中：ωi为断面权重；HDki为对应断面指标和谐度值。

计算得出黄河兰州段每季度的和谐度值见表9。

表9 每季度和谐度值Tab.9 Quarterly harmony degree values

再次进行加权平均计算，最终得2017年兰州段黄河水质和谐度HD=0.56。

2.7 确定最终结果

通过运用和谐度方程计算得出2017年兰州段黄河水质和谐度值，根据和谐度水质等级划分表(见表10)，确定出2017年兰州段黄河水质为Ⅲ类水，结果符合实际情况。

表10 水质和谐度划分标准Tab.10 Water quality harmony degree classification standard

3 结 论

(1)通过确定每季度和谐度，得出第一季度至第四季度和谐度以此增加，故应该重视第一季度各指标的变化情况，其对水质影响较明显。黄河水质监测的因素中，水温、浊度和电导率和谐度最低，与兰州段情况相符，因兰州段“冬长夏短”温差变化较大，上游黄土受长期冲刷导致黄河水泥沙含量高，既而水的纯净度低，水中含有能导电物质增加，使得电导率数值很高。在环境生态建设的前提下，应突出对黄河上游水生态的修复，提高黄河上游水环境，使得黄河水质逐渐得到改善。

(2)和谐度方程中的和谐系数i、不和谐系数j可根据实际情况进行灵活选择，综合评价方法存在一定的模糊性，不易用确定的模式评价问题，其自身灵活确定的特性，突出了和谐度方程综合评价方法的优势。

(3)本文运用和谐理论的定量表达方式和谐度方程(HDE)进行黄河兰州段水质评价，得出黄河兰州段水质为Ⅲ类水质，与黄河委员会2017年水质公报结果相对比，符合实际。其简便、灵活、符合实际的特点，避免了复杂的理论和实践要求，对在实际工作中易于操作，可以对其进行一定推广。

□