基于贝叶斯理论的土体抗剪强度参数最优二维分布模型识别方法
孙 骞,冯晓波
(1. 武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072;2. 武汉大学 水工岩石力学教育部重点实验室,武汉 430072)
0 引 言
很多工程可靠度分析涉及土体抗剪强度参数黏聚力c和内摩擦角φ,确定土体抗剪强度参数的概率分布模型是土体工程可靠度分析的重要前提,其概率分布模型的准确性直接影响着工程设计的安全性和经济性[1-3]。错误地使用某种分布当做真实分布模型可能会导致较大的设计偏差,造成严重的后果[4]。
近年来,Copula 函数为土体抗剪强度参数模型表征提供了新的方法[4]。文献中有许多表征相关结构的Copula函数,例如Gaussian、t、Plackett、Frank、Clayton和Gumbel Copula[4]。每一种Copula函数都有独立的结构。Copula理论认为任意联合概率分布可以分解为参数边缘分布函数和表示参数间相关结构的Copula 函数。该方法实现了土体体参数间相关结构的优化,有效减小了传统方法认为相关结构均服从Gaussian相关结构而带来的模型误差[5-11]。
一般情况下常用AIC(Akaike Information Criterion)准则来识别最优边缘分布和最优Copula函数,该方法认为在所有备选边缘分布和Copula函数中,具有最小AIC值的边缘分布和Copula函数即为最优边缘分布和最优Copula函数。值得注意的是,无论是AIC值,还是用于估计边缘分布参数和Copula函数参数的样本均值、标准差、相关系数都源于有限的试验数据,因此其准确性和可靠性取决于试验数据的样本大小[12]。试验表明,要想得到可靠的样本均值、标准差、相关系数,样本容量不得小于30[13];要想得到可靠的边缘分布和Copula函数识别结果,样本容量需要达到100[14]。众所周知,土体工程的样本量属于小样本,且通常小于30,从小样本中得出的二维分布模型显然是不可靠的。因此,基于小样本条件下的二维分布模型识别是一个具有挑战性的土体工程难题。
此外,在有限的样本外还可以得到一些先验信息,包括文献、工程师的判断、当地的工程经验等,这些先验信息有助于得到最优的二维分布模型。随着贝叶斯理论的发展,越来越多的研究者证实了贝叶斯理论能够充分地利用工程数据和先验信息,将二者有机结合来描述土体工程参数模型的不确定性,在土体工程小样本问题上是一种高效而实用的方法[21-25]。贝叶斯理论已被用于土体工程模型比较,例如利用贝叶斯理论识别土体中土层数目、土层厚度[15],利用贝叶斯理论识别出了表征土体参数空间变异性的自相关函数[16]。
但上述贝叶斯理论仅限于单参数。为了表征两个土体参数间的关系,Wang和Aladejare[17]采用贝叶斯方法导出单轴抗压强度(UCS)和杨氏模量(E)的联合概率分布。然而,他们直接使用二维正态分布模型来表征单轴抗压强度(UCS)和杨氏模量(E)的分布,假定单轴抗压强度(UCS)和杨氏模量(E)的分布均遵循单变量的一维正态分布,参数间相关性均遵循Gaussian Copula,完全没有考虑二维分布模型选择的不确定性。众所周知,土体参数不一定遵循单变量正态分布,他们可能遵循单变量对数正态分布、Gumbel分布等等。同样,土体参数间相关结构也不一定遵循Gaussian Copula,他们可能遵循Plackett Copula、Frank Copula、No.16 Copula等等。更重要的是,土体工程二维分布模型中边缘分布和Copula函数选择对于土体工程可靠度有重要的影响。过去的研究[18]表明,选择不同的边缘分布和Copula函数所产生的失效概率的差异为几个数量级。因此,在土体抗剪强度参数识别中,采用贝叶斯方法识别出最优二维分布模型具有重要的意义。
本文的目的在于提出基于贝叶斯理论的土体抗剪强度参数最优二维分布模型识别方法。简要阐述了在拥有一定先验信息和较少试验数据的情形下,贝叶斯理论识别最优二维分布模型的原理。采用蒙特卡洛模拟方法验证了贝叶斯理论识别最优二维分布模型的有效性。对比了贝叶斯独立识别、贝叶斯非独立识别、AIC一步识别,AIC两步识别4种识别方法的识别能力,并分析了影响贝叶斯理论识别精度的主要因素。最后,搜集了29组实际工程土体抗剪强度参数试验数据,研究了贝叶斯独立识别和非独立识别在实际工程土体抗剪强度参数最优二维分布模型识别中的应用。
1 表征土体抗剪强度参数相关结构的Copula方法
根据 Copula 理论,任意一个多元联合分布都可以由相应的边缘分布和一个 Copula 函数组合而成, Copula 函数明确了变量间相关系数的大小和相关结构的类型。对于土体抗剪强度参数c和φ来说,它们的联合概率分布函数F(c,φ)和联合概率密度函数f(c,φ)可以分别表示为[4]:
F(c,φ=C[F1(c),F2(φ);θ]=C(u,v;θ)
(1)
f(c,φ)=f1(c)f2(φ)D(F1,c),F2(φ);θ
(2)
式中:u=F1(c)、v=F2(φ)分别为c、φ的边缘累积分布函数;f1(c)、f2(φ)分别为c、φ的概率密度函数;C(u,v;θ)为Copula函数;φ为Copula函数的相关参数;D[F1(c),F2(φ);θ]=D(u,v;θ)=∂2C(u,v,θ)/∂u∂v为Copula密度函数。
Copula 函数构造联合分布模型的关键是确定Copula 函数相关参数和识别最优Copula 函数。在确定Copula 函数相关参数时常采用秩相关系数法。Kendall 秩相关系数τ与Copula 函数C(u,v;θ)的关系式为[4]:
(3)
因此给定Kendall 秩相关系数 便可通过公式(3)求出参数θ。
在识别最优Copula 函数方面,本文选取Gaussian、Plackett、Frank 和 No.16 Copula 函数来描述土体抗剪强度参数的统计负相关性[5-11]。它们的 Copula函数和参数取值范围见表1。
2 土体抗剪强度参数最优二维分布模型识别的AIC准则
2.1 AIC一步识别
根据AIC准则定义,具有最小AIC值的二维分布模型被认为是最优二维分布模型。AIC一步识别是指同时识别出土体抗剪强度参数二维分布模型中最优边缘分布和最优 Copula 函数。由于AIC 值定义为试验数据点处二维分布模型密度函数值对数和的负 2倍与 2 倍二维分布模型参数数目之和,故AIC一步识别的计算表达式为[19]:

表1 4种Copula函数和参数取值范围Tab.1 Summary of adopted 4 copula functions and
(4)
式中:Nd为试验数据的样本数目;m为二维分布模型中参数的数目,模型中共包含μc、σc、μφ、σφ、θ等参数,所以m=5;(ui,vi)为土体抗剪强度参数试验数据(ci,φi)的经验分布值,将土体抗剪强度参数试验数据D={(ci,φi),i=1,2,…,Nd} 转化为标准均匀分布变量U={(ui,vi),i=1,2,…,Nd}的目的是为了方便计算,具体的计算公式为:
(5)
Rank为排序函数,排列顺序为升序。
此外,AIC准则中涉及的均值、标准差和相关系数是基于试验数据采用极大似然估计方法得到的。
2.2 AIC两步识别
AIC的两步识别顾名思义是先识别出边缘分布模型,再识别出Copula 函数,具有最小AIC值的边缘分布模型和最小AIC值的Copula 函数组合后即为最优的二维分布模型。识别边缘分布模型的公式为[19]:
(6)
(7)
式中:Nd为试验数据的样本数目;m为边缘分布模型中参数的数目,本文所选边缘分布模型中的参数包括μ、σ,所以m=2。
识别Copula 函数的公式为:
(8)
式中:Nd为试验数据的样本数目;m为Copula 函数中参数的数目,由于本文 4 种备选 Copula 函数都是单参数 Copula,因此m=1。
3 土体抗剪强度参数最优二维分布模型识别的贝叶斯方法
基于Copula 理论构造的二维分布模型可以拆分为两个边缘分布和一个Copula函数,通常根据土体抗剪强度参数二维分布模型中最优边缘分布和最优 Copula 函数是否被同时识别出将识别方法分为两种:一步识别法和两步识别法。贝叶斯一步识别需要五维积分,单次识别耗时长,计算效率低。两步识别是指首先识别出表征参数c和φ的边缘分布,再识别出表征参数间相关性的 Copula 函数。两步识别法在识别过程中避免高维积分的运算,大大提高了计算效率。对于工程师而言,计算效率的高低是决定是否采用该种识别方法的关键所在,能在可接受的精度范围内快速得出结论才是最重要的,所以本文只研究贝叶斯两步识别。根据贝叶斯两步识别中第二步识别过程与第一步识别过程是否有关,分为贝叶斯两步独立识别和贝叶斯两步非独立识别。显然,独立识别指前后两步识别没有关系,非独立识别指第二次识别过程基于第一步的识别结果。为了简化表达,文中用贝叶斯独立识别和贝叶斯非独立识别分别代替贝叶斯两步独立识别和贝叶斯两步非独立识别。
3.1 边缘分布的识别
根据前人的研究成果,本文的备选边缘分布类型采用正态分布、对数正态分布、极值Ⅰ型分布、伽马分布,其对应的分布函数和概率密度函数如表2所示。

表2 4种边缘分布的分布函数和概率密度函数Tab.2 Summary of distribution and their probability density functions of 4 marginal distributions
下面以黏聚力c为例详细阐述贝叶斯识别方法。
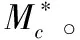
(9)
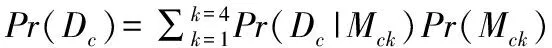
当边缘分布模型Mck中参数μc、σc未知时,可利用全概率公式将Pr(Dc|Mck)表示为:
(10)
式中:Pr(Dc|μc,σc,Mck)为给定Mck及其参数μc、σc条件下Dc发生的概率;Pr(μc,σc|Mck)为参数μc、σc的概率密度函数。假设Dc为黏聚力参数的Nd次独立同分布观测,那么Pr(Dc|μc,σc,Mck)可以表示为试验数据点处备选边缘概率函数的乘积:
(11)
当先验信息较少时,根据最大熵原理,通常假定μc、σc服从二维均匀分布,则概率密度函数Pr(μc,σc|Mck)的计算公式为:
(12)
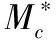
3.2 Copula函数的识别
Copula 函数识别前需要确定的要素有:参数u和v数据,先验信息以及备选 Copula 函数模型。参考前人研究成果,本文选取 Gaussian、Plackett、Frank 和No.16 Copula 函数为表征土体抗剪强度参数相关结构的 Copula 函数,则C={Ck,k=1,2,3,4}={Gaussian, Plackett, Frank, No.16}。分别计算这4种备选 Copula函数Ck在给定土体抗剪强度参数试验数据D={(ci,φi),i=1,2,…,Nd}条件下发生的概率Pr(Ck|D)。根据贝叶斯理论的基本原理,具有最大发生概率Pr(Ck|D)的Copula 函数即为最优Copula 函数。
(13)
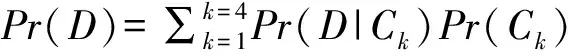
当Copula 函数Ck中参数θ未知时,可利用全概率公式将Pr(D|Ck)表示为:
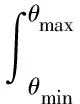
(14)
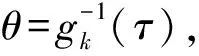

(15)
式中:Pr(D|τ,Ck)为给定Ck及τ在的条件下D出现的概率;Pr(τ|Ck)为τ的概率密度函数。同理,可假设τ在区间[τmin,τmax]内服从均匀分布,则Pr(τ|Ck)=1/(τmax-τmin)。假设D为独立同分布观测,那么Pr(D|τ,Ck)可以表示为试验数据点处备选Copula 密度函数的乘积:
(16)
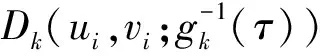
显然,在贝叶斯理论框架下识别Copula函数的首要任务是确定变量U={(ui,vi),i=1,2,…,Nd}。由Copula函数的定义可知, Copula 函数的边缘分布在区间[0,1]上服从均匀分布。根据变量U确定方法的不同,贝叶斯方法分为独立识别和非独立识别。独立识别指两步识别没有依赖关系,非独立识别指第二步识别以第一步识别结果为基础。
3.2.1 独立识别
由于第一步识别和第二步识别没有关系,所以变量U是基于原始数据的经验分布值确定的。由公式(5)将数据D={(ci,φi),i=1,2,…,Nd}转化为标准均匀分布变量U={(ui,vi),i=1,2,…,Nd}。
3.2.2 非独立识别
根据Copula理论可知,在变量U中u和v可分别视为参数c和φ的累积分布函数,即u=F1(c|μc,σc)和v=F2(φ|μφ,σφ)。第一步边缘分布模型识别后可以确定参数c和φ的累积分布函数类型,在确定μc和σc以及μφ和σφ后便可以确定c和φ的累积分布函数F1(c|μc,σc)和F2(φ|μφ,σφ)。下面以参数c为例详述如何在已知累积分布函数类型后得到μc和σc的最可能值,下文简称MPV值。依据贝叶斯原理可得出μc和σc的后验分布为:
(17)
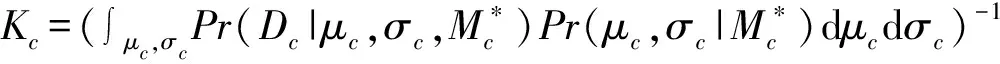
4 最优二维分布模型识别方法的对比
本节采用蒙特卡洛模拟方法验证贝叶斯理论识别最优二维分布模型的有效性。为了验证该方法的有效性,将贝叶斯识别结果与AIC 准则识别结果进行对比。试验表明1 000 次模拟能够得到非常稳健的最优二维分布模型识别结果,所以本节试验方案设计为:在给定真实二维分布模型情况下,重复模拟1 000组样本数目为Nd的服从给定真实二维分布模型的样本,分别采用贝叶斯独立识别、贝叶斯非独立识别、AIC一步识别、AIC两步识别共计4种方法给出每组样本的最优二维分布模型,最后统计并对比1 000次模拟样本中真实二维分布模型被识别为最优二维分布模型的次数。本文拟采用正态(Normal)分布、对数正态分布(Lognormal)、极值Ⅰ型(Gumbel)分布、伽马(Gamma)分布作为模拟算例的边缘分布类型,选取Gaussian、Plackett、Frank 和No.16 Copula 函数为表征模拟算例土体抗剪强度参数相关结构的 Copula 函数,分析这4种方法的识别能力与不同真实二维分布模型、样本数目以及参数相关性的关系。对于真实二维分布模型,假定μc=66,σc=22,μφ=28,σφ=3.5。选取样本数目Nd分别等于 30、50和100以及相关系数τ分别等于-0.25、-0.50 和-0.75 ,因此c和φ各4种备选边缘分布模型、4种Copula 函数构成了4×4×4×3×3=576种备选二维分布模型,再加上3种样本数目和3种相关系数,共组成 组模拟方案。表3 给出了 64 种备选二维分布模型。
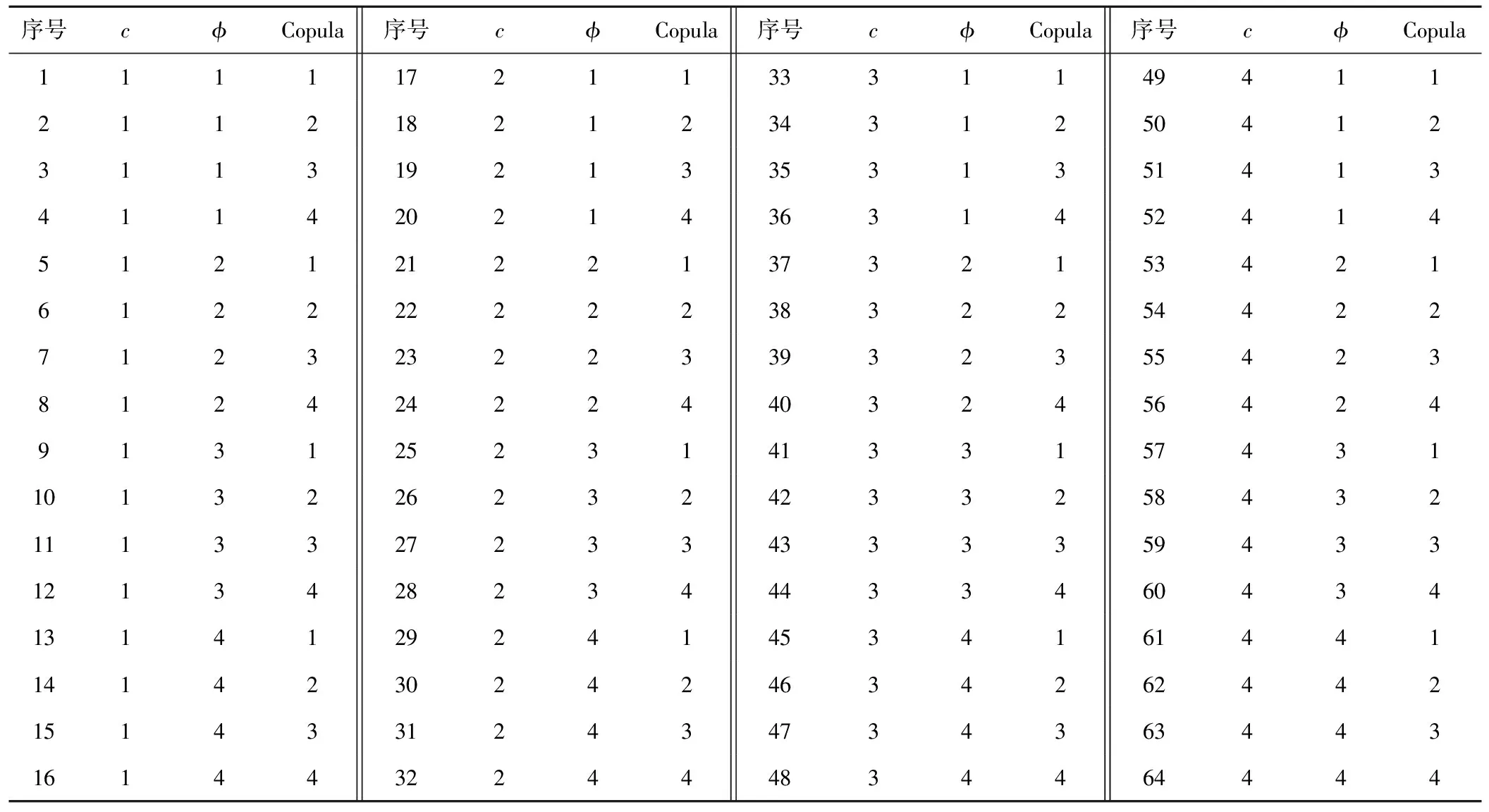
表3 64种备选二维分布模型Tab.3 64 kinds of alternative bivariate distribution models
注:在c和φ中, “1”,“2”,“3”和“4”分别代表“正态(Normal)分布”,“对数正态(Lognormal)分布”,“极值Ⅰ型(Gumbel)分布”和“伽马(Gamma)分布”;在Copula中,“1”,“2”,“3”和“4”分别代表“Gaussian”,“Plackett”,“Frank”和“No.16”。
这里假设64种备选二维分布模型的先验概率相等,由于本文采用两步识别,每步识别中的备选模型数量均为4,因此先验概率皆为1/4。在每组方案模拟的1000组样本中,当真实的二维分布模型被识别为最优二维分布模型的次数大于其余63种模型时,认为识别成功;否则认为识别失败。表4为上述模拟试验中4种方法的识别结果。
如表4所示,经对比发现,相同条件下两种贝叶斯方法成功识别的概率均高于两种AIC方法成功识别的概率。
就单个模型在1 000次模拟试验的识别精度而言,贝叶斯方法也优于AIC准则。由于模型种类多,且4种识别方法的识别精度规律保持相对稳定,所以只选取了部分试验数据作图1来展示4种方法识别精度的高低。
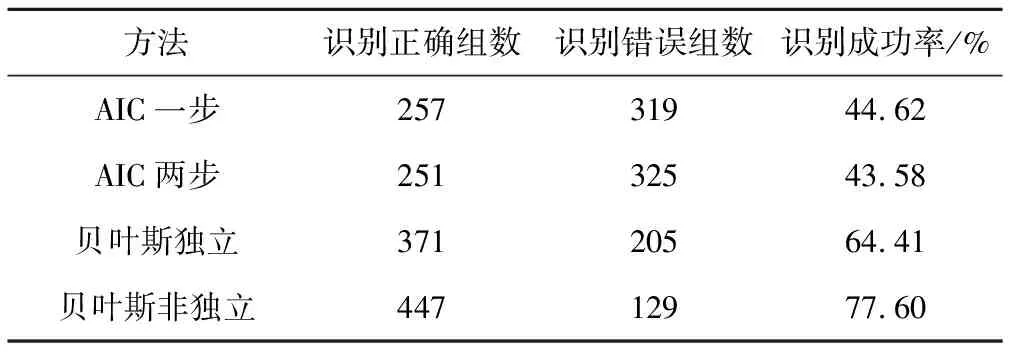
表4 576组模拟试验中4种方法成功识别真实二维分布模型的组数Tab.4 Number of successful identifications over 576 types using Bayesian method
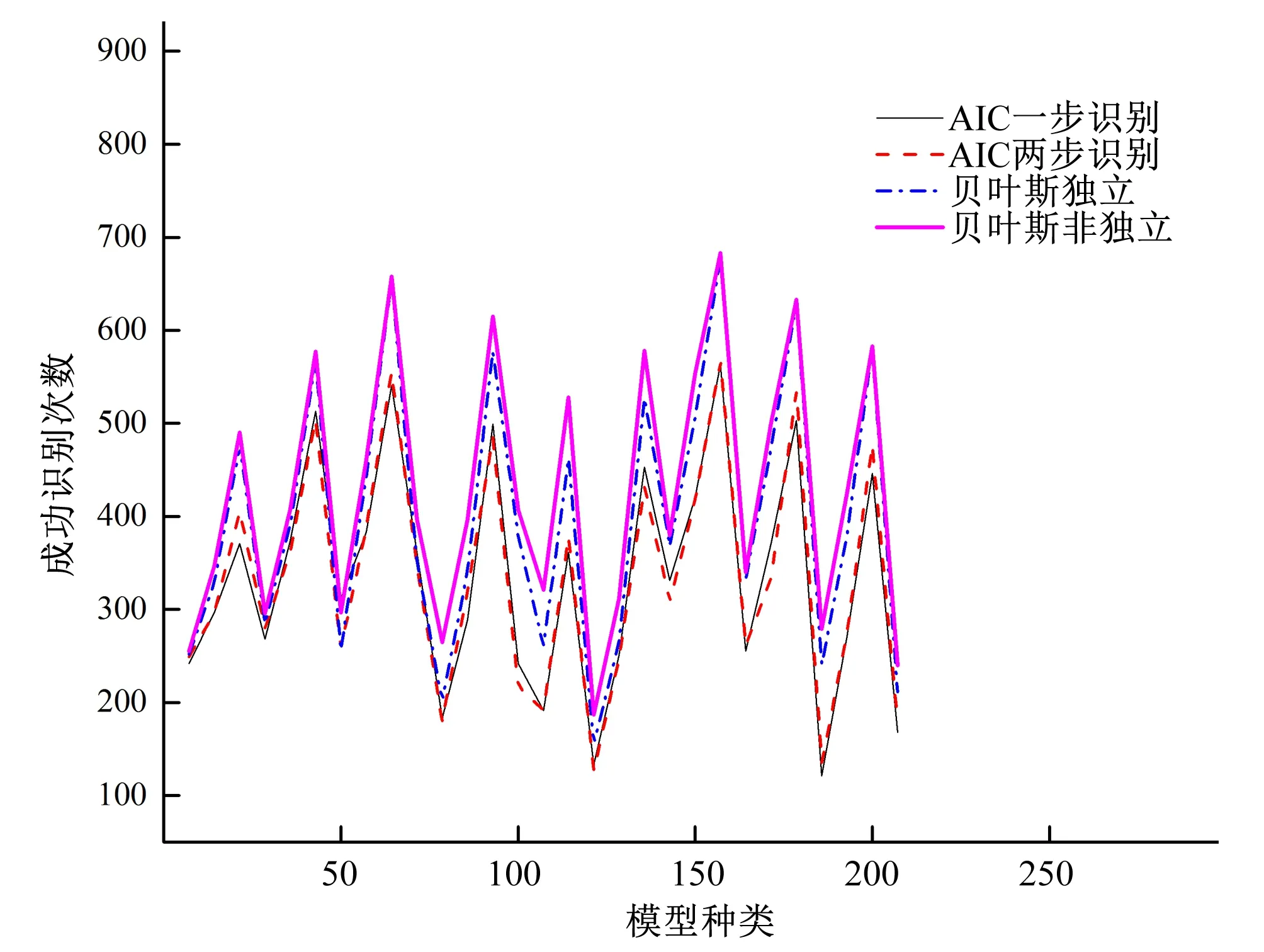
图1 4种识别方法成功识别次数比较Fig.1 Number of successful identifications of 4 methods
显然,两种贝叶斯识别方法的识别精度普遍优于两种AIC识别方法的识别精度,且贝叶斯非独立识别在多数情形下优于贝叶斯独立识别,AIC一步识别和两步识别在识别精度上并无明显差异。造成贝叶斯独立识别和非独立识别精度差异的主要原因是Copula函数的变量不同。以小浪底大坝斜心墙三轴固结排水(CD)土体抗剪强度参数数据为例,通过两种方法得到变量U,变量U的分布情况如图2所示。由图2可知,两种方法使用的变量U在整体趋势上一致,但是并不完全相同, Copula函数的变量不同导致了识别结果的差异。由于这4种方法在计算机上运行一次的速度均在3秒以内,所以在识别土体抗剪强度参数最优二维分布模型时,建议优先采用贝叶斯非独立法进行识别。
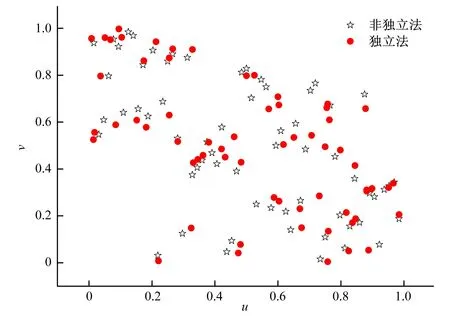
图2 贝叶斯独立法和非独立法中Copula函数变量散点图Fig.2 Scatter plots of Copula function in Bayesian theory bivariate distribution identification
5 影响识别精度的因素分析
前文验证了贝叶斯非独立识别方法对最优二维分布模型识别的高效性,下面进一步分析影响该方法识别精度的主要因素。比较后发现,影响最优二维分布模型识别精度的主要因素是样本数目、参数间相关性、备选二维分布模型集合。当然,备选二维分布模型的先验概率对真实二维分布模型的识别结果也有明显的影响。由于篇幅有限,图3仅展示了4种真实二维分布模型的识别结果,真实二维分布模型分别为[1,1,1]、[1,1,2]、[1,1,3]、[1,1,4]。
5.1 样本数目
从图3(a)~3(d)中可以看出,真实二维分布模型被识别为最优二维分布模型的次数随样本数目的增加而增大。此外,当样本数目逐渐增大时,单位样本数目的增加对于识别精度的提高效果逐渐减小,这说明识别精度在样本数目较少时对样本数目的变化更敏感。因此若能在实际工程中获得更多的土体抗剪强度参数试验数据,则可以得到更可靠的二维分布模型,提高工程设计的可靠度。
5.2 参数间相关性
从图3(a)~3(d)中可以看出,参数间相关性对最优二维分布模型的识别结果具有重要的影响。参数间相关性主要是通过影响Copula函数的识别从而影响二维分布模型的识别。通过对比发现,当真实Copula函数为Gaussian、Plackett 和 Frank Copula 函数时,真实二维分布模型被识别为最优二维分布模型的次数随参数间负相关系数的增加而增大。而当真实Copula函数为No.16 Copula 函数时,真实二维分布模型被识别为最优二维分布模型的次数随参数间负相关系数的增加而减小。这是因为大多数Copula函数在相关系数趋近于0时都收敛于独立 Copula 函数,此时不同的Copula函数差异性很小,可以忽略,当相关系数的绝对值逐渐增大时,不同的Copula函数差异性也随之增大,因此更容易识别,本文中Gaussian、Plackett 和 Frank Copula 函数便属于这一类;当然,还存在少数的Copula函数,它们在相关系数趋近于0时不收敛于独立 Copula 函数,且当相关系数的绝对值逐渐增大时,它们与其他Copula 函数的差异性逐渐减小,因此识别难度增加,本文中No.16 Copula 函数便属于这一类。因此,参数间相关性大小对于最优二维分布模型的识别精度没有完全统一的规律,换言之,大部分二维分布模型的识别精度随相关性的增加而增大,少数二维分布模型的识别精度随相关性的增加而降低。
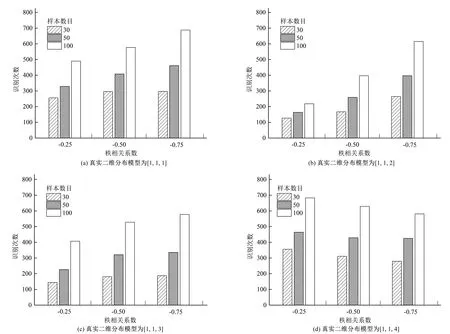
图3 4种真实二维分布模型识别能力对比图Fig.3 Identification ability of 4 real bivariate distribution models
5.3 备选二维分布模型集合
前文分析了参数间相关性对二维分布模型识别精度的影响。由于真实二维分布模型只选取了一种边缘分布类型,故只分析备选二维分布模型中Copula 函数的差异对识别能力的影响。对比图3(a)~3(d)不难发现,图3(a)和图3(d)的成功识别次数明显高于图3(b)和图3(c),这是因为一般来说, Plackett 和 Frank Copula 函数在相关系数相同时具有相似的相关结构,而 Gaussian 和 No.16 Copula 函数相关结构与其余 3 种备选 Copula 函数存在较大差别。因此,当真实Copula函数为Gaussian或No.16 Copula 函数时,真实二维分布模型被识别为最优二维分布模型的次数远远大于真实Copula函数为 Plackett 或Frank Copula 函数的二维分布模型。因此,真实 Copula 函数与其余备选 Copula 函数之间存在的差异越大就越容易被识别成功,需要的样本数目越少。
5.4 先验信息
由于信息缺乏,前文的分析假定64 种备选二维分布模型的先验概率都相等。当有足够的证据表明某种二维分布模型作为最优二维分布模型的概率明显大于其他二维分布模型作为最优二维分布模型的概率时,应代入不等的先验概率进行计算。就本文的模拟试验而言,由于样本均生成于真实的二维分布模型,故样本来自于真实二维分布模型的概率明显大于其他备选二维分布模型。
假定真实二维分布模型的概率为2/5,剩余63种备选模型均为1/5,相关系数τ=-0.5。计算结果如图4所示:
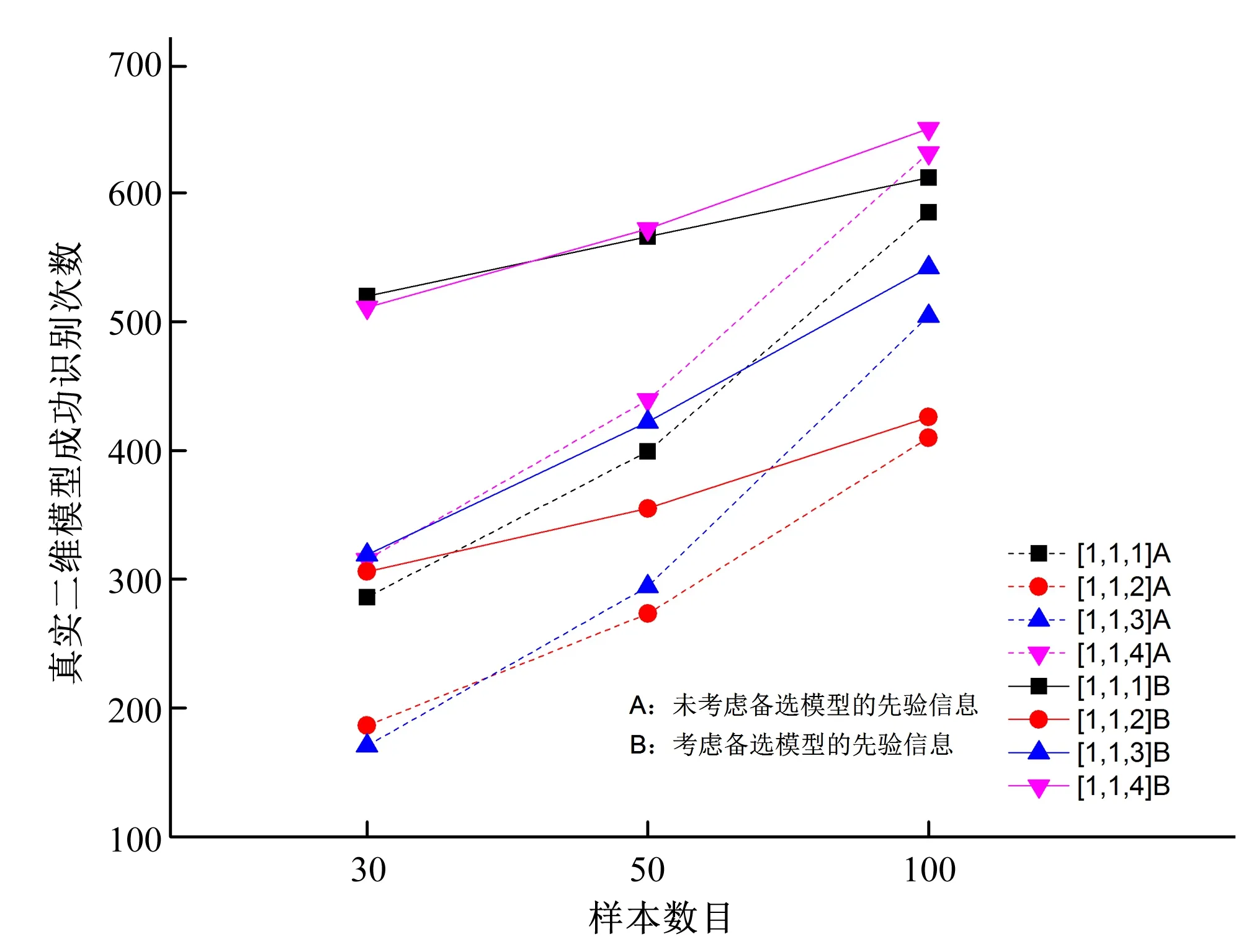
图4 先验信息对识别精度的影响Fig.4 The prior information influences on identification
从图4中可知,考虑不相等的先验概率的识别结果明显优于相等的先验概率的识别结果,真实二维分布模型被识别为最优二维分布模型的概率显著提高。
6 工程应用
本节探讨贝叶斯理论在实际工程土体抗剪强度参数最优二维分布模型识别中的应用。本文共搜集了全世界范围内 29 组土体抗剪强度参数的现场或者室内试验数据,大部分的试验数据的样本数目小于30,属于小样本。本文提出的基于贝叶斯理论的土体抗剪强度参数最优二维分布模型识别方法相较AIC准则的识别方法能在小样本条件下更有效地识别出最优二维分布模型。本节选择小浪底大坝斜心墙三轴固结排水(CD)土体抗剪强度参数数据为例,阐述基于贝叶斯理论识别最优二维分布模型的计算步骤:
(1)获取土体抗剪强度参数试验数据D={(ci,φi),i=1,2,…,63} 转化为标准均匀分布变量U={(ui,vi),i=1,2,…,n}。
(2)土体抗剪强度参数存在较强的统计负相关性,Kendall 秩相关系数τ=-0.38。选取本文中的64种二维分布模型为备选模型,设定τ的积分区间为[-1,0],此时τmin=-1,τmax=0。
(3)采用公式(9)计算出64种备选模型在给定试验数据D条件下的后验概率Pr(Mk|D), 具有最大后验概率的备选模型即为最优二维分布模型。
对于黏聚力c而言,根据公式(9)分别计算正态分布、对数正态分布、极值Ⅰ型分布、伽马分布发生的概率分别为: 96.88%、 0.12%、 2.54%、 0.46%,因而表征本例中黏聚力边缘分布的最优模型为正态分布;对于内摩擦角φ而言,正态分布、对数正态分布、极值Ⅰ型分布、伽马分布发生的概率分别为:30.69%、 18.42%、 2.08%、48.81%,因而表征本例中内摩擦角边缘分布的最优模型为伽马分布;同理,对于Copula函数而言,Gaussian、Plackett、Frank 和No.16发生的概率分别为:24.81%、 32.26%、 42.66%、 0.27%,因而表征本例中Copula函数的最优模型为Frank Copula函数。可见,黏聚力边缘分布为正态分布,内摩擦角边缘分布为伽马分布,相关结构为Frank Copula函数的二维分布模型为64种备选模型中能最优地表征小浪底枢纽工程固结排水(CD)土体抗剪强度参数试验数据二维分布的模型。表5给出了模拟样本c和φ的均值和标准差,等效样本的统计量均值和标准差与原始样本数据相比,其相对误差都在1%以内,模拟数据的Kendall 秩相关系数 ,与样本数据相比相对误差仅为2.63%,这些微小的相对误差说明蒙特卡洛模拟样本能够比较准确地还原原始样本的数据特征。图5给出了模拟数据和样本数据的分布情况,从图5中可以看出,模拟数据基本覆盖了样本数据的分布区域,两者拟合度良好,能够有效地反映试验数据的二维分布情况。
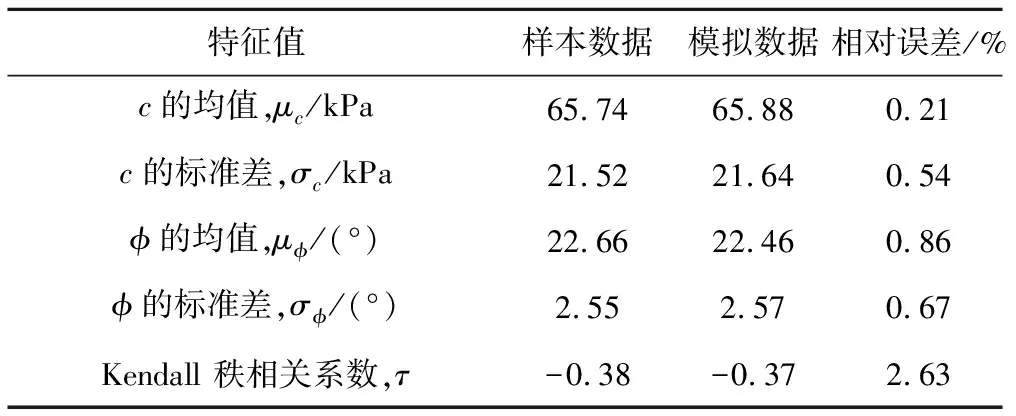
表5 土体抗剪强度参数模拟样本的统计特征值Tab.5 Statistical feature values of shear strength parameter simulation samples
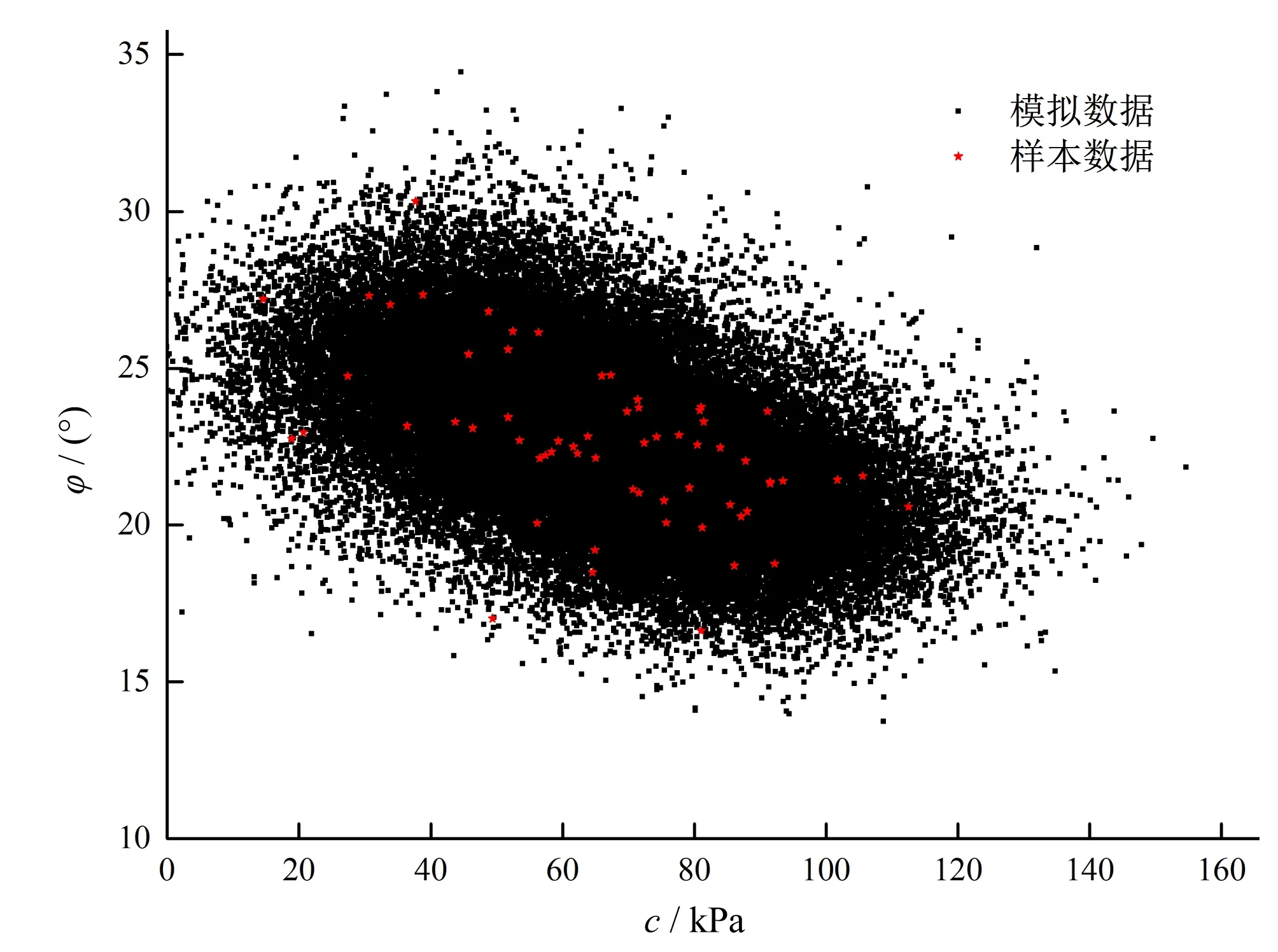
图5 土体抗剪强度参数等效样本散点图Fig.5 Scatter plots of shear strength parameter simulation samples
重复以上3步,即可得出29组数据对应的最优二维分布模型,计算结果见表6,该表统计了贝叶斯独立和非独立两种方法的识别结果。经统计,黏聚力的最优分布模型依次为:正态分布,伽马分布,对数正态分布和极值Ⅰ型分布;对于内摩擦角的最优分布模型依次为:正态分布,伽马分布,极值Ⅰ型分布和对数正态分布;表征参数相关结构的最优Copula 函数依次为: Gaussian, Frank, Plackett, No.16。可见在实际工程中土体抗剪强度参数存在各种类型的分布情况,要具体工程具体分析,不能一概而论,否则在计算土体结构物可靠度时会低估或高估实际失效概率,造成工程失事风险或工程资源浪费,这进一步证明了考虑土体抗剪强度参数二维分布模型的不确定性是非常有必要的。
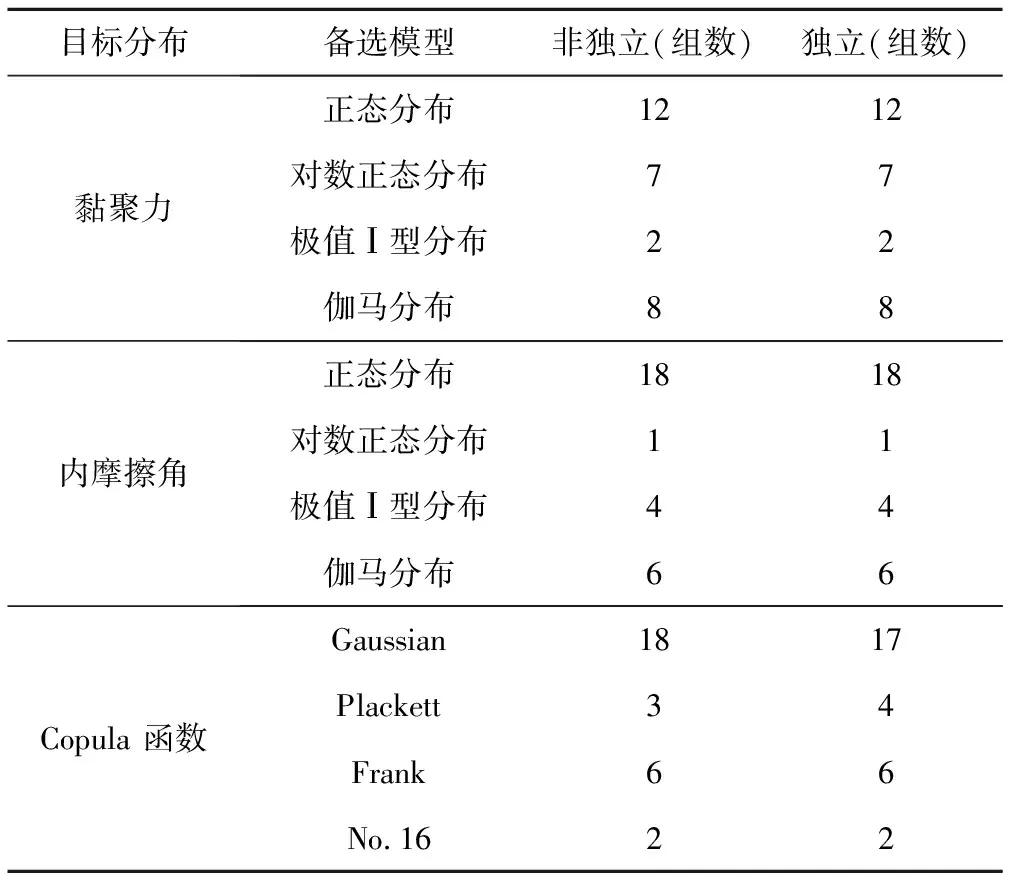
表6 29组工程数据贝叶斯独立识别和非独立识别的结果统计Tab.6 Summary of 29 sets of shear strength parameters and the results of their best-fit models
7 结 论
(1)贝叶斯理论能够有效地识别表征土体抗剪强度参数最优的二维分布模型。该方法识别二维分布模型时,不需要估计二维分布模型的参数,并能与工程上现有的工程经验等先验信息相结合,为降低模型选择的不确定性提供了一条高效且稳定的途径。
(2)与常用的基于AIC准则的识别方法相比,贝叶斯理论在识别能力和识别精度上表现更出色,特别是在样本数目较小的情况下,贝叶斯理论的优势表现得更为明显。其中贝叶斯非独立识别方法可以认为是兼顾识别能力和识别精度的最优选择。
(3)土体抗剪强度参数的样本数目、参数间相关性、备选二维分布模型集合以及先验信息都显著影响贝叶斯理论的识别精度。通常,样本数目越大、参数间相关性越强、备选二维分布模型集合中真实 Copula 函数与其余备选Copula 函数差异越大、真实二维分布模型具有越高的先验概率,贝叶斯理论的识别精度就会越高。
□

