基于贪心算法的城市地下物流系统网络节点选址

方龙祥 于雪雨

（安徽师范大学 数学与统计学院，安徽 芜湖 241002）

0 引言

当今社会，货物运输占公路交通的比例较大，极大的增加了交通压力。仅仅扩充地面路网等措施面临解决不了本质问题，亟需创新型的解决思路。“城市地下物流”虽然没有大范围普及,但是已有部分学者已经分析了城市地下物流系统的各方面优势[1-5]。一方面，地下物流系统项目多使用专门的货物运输线路，可以避免外界的干扰。同时，货物在地下运输噪音较小，对居民干扰较低，居民生活品质可以得到一定的提升。另一方面，地下物流系统在提升城市物流效率方面的作用也很显著，将城市大型零售企业的货物配送交给城市内部的地下物流系统来完成，这样可以实现网络相互连接。显然，构建城市内部的地下物流系统对于解决城市交通拥堵、环境恶化等问题十分有必要。近些年来我国的物流行业伴随着电子商务的兴起得到了迅猛发展，但是市场倒逼的发展缺少规划，物流行业的矛盾问题依然较多。竞争无序、基础设施落后、物流网络混乱、经验管理粗放等现象明显。像荷兰、美国、日本等世界上一些较为发达的国家已经对城市地下物流系统有了较为深入的研究和实践，对城市地下物流系统的数字化搭建、网络构架、工程技术等板块，都有了一定的研究成果[2]。这些研究在理论层面论证了城市地下物流系统具有运行速度快、准确率高的特点。由此，基于改善和缓解城市问题，实现城市可持续发展基础上，以合肥市二环及周边区域的数据为例，通过构建集合覆盖模型并采用贪心算法研究了城市地下物流系统网络节点的选择。

1 问题的提出

网络节点是整个地下物流系统网络的核心，节点的选择最终将会影响到整个物流系统的效率，所以在确定节点时要充分考虑各种因素，不仅要与商品的流向一致，而且也要考虑建立的网络节点与现有地面物流节点的竞争情况。地下物流系统网络节点选择应遵循：（1）尽可能的将节点选在靠近用户的地区；（2）物流节点不能选在地面建筑物下方，以免破坏现有建筑物的基础；（3）地下物流节点的最小深度要有明确的规定；（4）工业用地、商业用地的边缘可以选为物流节点，且应该尽量靠近工业区或商业区；（5）可以在农业区或者未开发的区域选择网络节点。因此在规划网络节点的时候要具有前瞻性，要与城市的发展规划相结合。网络路线要连接城市的港口、码头、办公区域、大型生活居民区、商圈等平时货流量较大的区域。另外还要考虑城市目前的轻轨建设及地面物流中心、物流基地的规划情况等。

本研究是已知一组货物需求点与货物供应点，网络节点是从货物供应点中选择，要求选中的网络节点数最少且能够辐射所有的需求点，以节省项目前期的建设成本，这是典型的集合覆盖问题。集合覆盖模型指的是：在已知一组需求点和供应点的情况下，建立目标函数并设定约束条件，用最少数量的供应点为这些需求点提供服务[3]。

2 研究设计

2.1 模型构建

为了便于讨论，这里放松IP变量的整数性要求，得到了它的松弛线性规划问题，令LP代表此规划问题的模型：

2.2 模型求解

集合覆盖模型是一种典型的组合优化模型，它要求用最少的网络节点将所有需求点实现全覆盖。遗憾的是集合覆盖问题在算法复杂性上属于非确定性多项式难题（NP-hard），即它不存在多项式时间复杂度内的精确算法[5]。当问题的规模较大时求解这类问题大多采用近似算法如0-1算法、贪心算法等。

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，而是在某种意义上的局部最优解。其基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。我们为模型设计如下贪心算法[6]：

上述算法可以描述为：从给出的货物供应点中选择一个点，使它覆盖最多的需求点，即便这些需求点已经被一些供应点覆盖也无妨。重复第一步，直到覆盖了所有的需求点[6]。可以看出贪心算法的求解过程是一种从局部最优解到全局最优解的逼近过程。

2.3 数据来源

地下物流系统还处于理论分析与预测阶段，较难获得精确的数据资料。本研究实证分析部分主要是对合肥市较为拥堵区域 （合肥二环及周边区域）的地下物流系统网络节点进行初步探索。所以物流供需点选在合肥市二环及周边人流量较大的区域如生产用地、仓储用地、居民区、商业中心等。选中的供需点如图1。这里提取了各点的坐标如表 1，并进行了相关的整理。 其中：Si（i=1，2，3，…，21）为货物供应点；ei（i=1，2，3，…，21）为货物需求点。

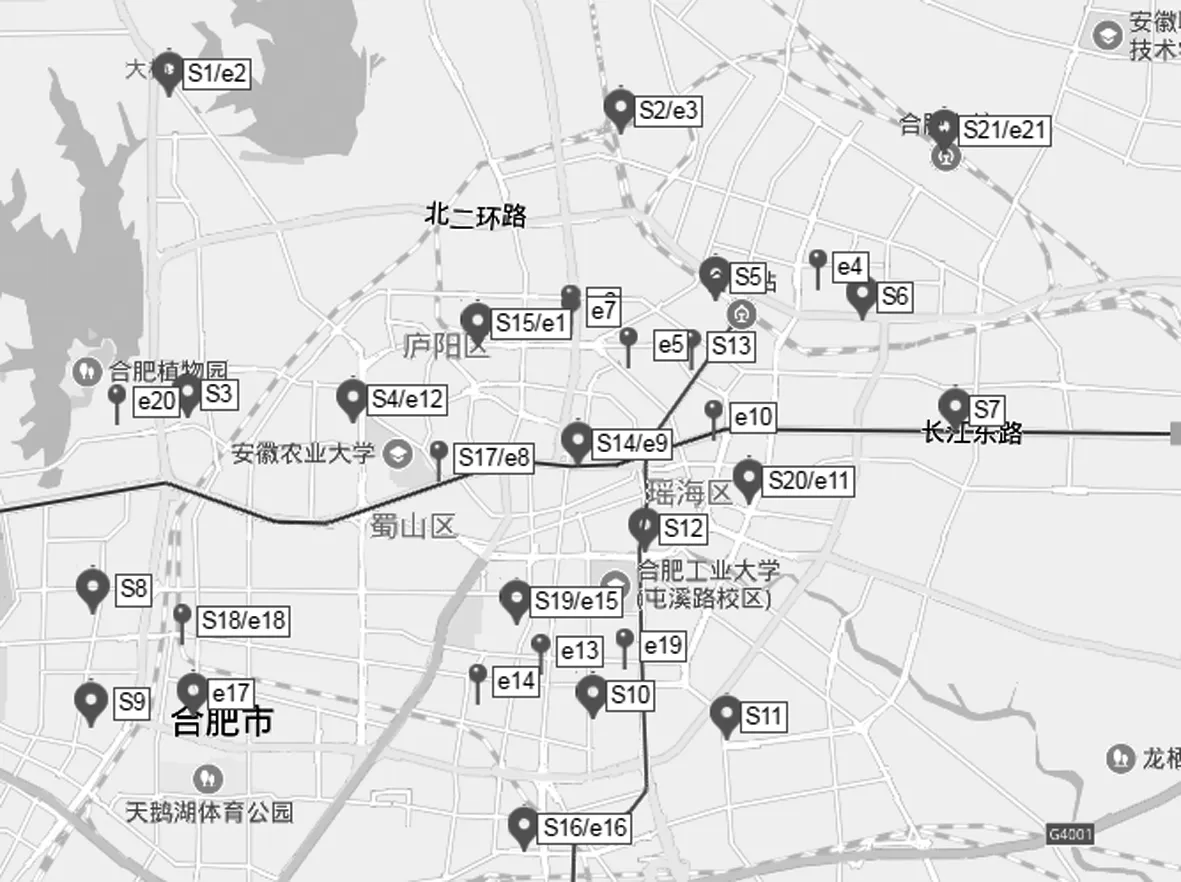
图1 货物供应点与需求点坐标

表1 各货物供应点与需求点经纬度

根据合肥市供应点与需求点的分布经纬度坐标表1，在地图上进一步测量了供应点到需求点的距离如表2：

表2 货物供应点到需求点的距离

由以往研究可知，地下物流系统网络节点的服务半径为3 km～5 km，这里假定节点的服务范围为3 km，结合表2（货物供应点到需求点的距离）得到各货物供应点到需求点的可达矩阵如表3：

表3 供应点到需求点的可达矩阵

令可达矩阵为A=aij，其中aij=1或aij=0，表示第j列供应点覆盖了第i行需求点或者第j列供应点没有覆盖第i行需求点。

2.4 实证分析

根据上面的各货物供应点到需求点的可达矩阵，找到所有候选的货物供应点可以提供服务的所有需求点的集合，它们到达货物供应点的距离均小于等于3 km。如表4所示：

表4 需求点集合

从上面给出的货物供应点中选择一个点，使它覆盖最多的需求点，即便这些需求点已经被一些供应点覆盖也无妨。重复第一步，直到覆盖了所有的需求点。这是一种从局部最优解到全局最优解的逼近过程。贪心算法的实现我们这里借助python2.7，求解程序及结果截图如下：

图2 贪心算法运行结果图

从上面的运行结果可知贪心算法最终得到的结果是从21个供应节点中选择8个供应节点，这8 个供应节点分别是 S1，S2，S3，S6，S9，S10，S13，S14，确定的网络节点如图3（注：小红旗代表选中的网络节点）。

图3 贪心算法确定的网络节点分布图

3 研究结论

根据已有研究[7]，基于0-1整数规划算法得到最少需要 S1，S2，S3，S6，S10，S13，S17，S18 这 8 个网络节点才能全覆盖所有货物需求点。对比上述两种算法的求解结果可知，贪心算法与0-1整数规划算法都选择了8个网络节点。两种算法均选择的网络节点是 S1，S2，S3，S5，S10，S13， 选择的网络节点仅在S18与S9，S17与S14上存在区别。在选择网络节点时，要将合肥市目前物流企业的分布情况考虑进来：合肥市的物流基地及物流园大部分分布在离两环较远的西南方向，一小部分分布在合肥市的东北方向及其他各处。大型的物流园及物流基地离合肥市中心较远，且大多数物流园、物流中心、物流基地离合肥市中心的距离相比于备选节点之间的距离要远的多。为了节省后期的运输成本，在选择网络节点时要尽可能的靠近上述两个方向。所以贪心算法在西南方向选择的网络节点S9比0-1整数规划算法选择的节点S18合适。同时，也不能忽略合肥市一环最为繁华、人流量最大的区域是淮海路步行街。这里在相同情况下会比其他地方的人流量、货流量大，在此建设网络节点会大大降低后期的货物周转成本。所以，贪心算法在此模型中选择的网络节点S14较0-1整数线性规划算法选取的节点S17更可取。综上，本文选择贪心算法确定的货物供应点作为合肥市二环及周边地下物流系统网络节点更合理，更符合实际。