基于阻尼参数的高速铁路连续梁桥地震损伤概率影响分析

向宝山,崔恩旗,曹艺缤,李 鑫

(1.西南交通大学土木工程学院,成都 610031； 2.四川省交通运输厅公路规划勘察设计研究院,成都 610041)

引言

地震不但对人民生命财产安全造成重大破坏，而且也使得作为交通基础设施的桥梁工程遭受到不同程度的损伤或毁坏。一旦灾区桥梁被毁坏，将阻断抗震救灾的生命线工程，造成更加严重的后果。因此，对现存桥梁进行地震易损性分析显得格外重要，这会对抗震加固及震后桥梁安全评价提供一定参考。

对于地震作用下桥梁易损性的研究，主要采用易损性曲线的方式。国内外学者已做了大量相关研究[1-16]，这些研究根据各种桥型，以不同的破坏准则及损伤指标，采用非线性动力时程分析，建立了易损性曲线。黄志堂[17]对叠合柱高墩连续刚构桥采用17条地震波进行了地震易损性分析，并根据可靠度理论推导全概率和半概率地震易损性解析表达式，进行了概率损伤风险分析和性能评估。李鑫[18]研究了材料参数和阻尼器参数对高速铁路连续梁桥地震易损性的影响。王炎[19]以简支梁桥为背景，对铁路减隔震桥梁的抗震设计理论、抗震性能以及地震易损性进行了系统的研究。

桥梁由于设置阻尼器后，阻尼器吸收部分地震能量，使得桥墩曲率下降，活动支座位移得到了控制，地震作用下桥梁的受力较未设置阻尼器时更为合理，桥墩和支座的损伤概率有较大的下降，能够提高桥梁的抗震性能，减小了地震作用下的损伤概率。因此以一座高速铁路连续梁桥为工程背景，基于开源程序OpenSees建立数值模型，研究阻尼系数及阻尼指数对桥梁地震易损性的影响。

1 易损性基本理论

桥梁的地震易损性曲线基于桥梁构件的地震时程结果来获得。根据Cornell的建议，地震需求D与地震动强度M之间的关系满足下式

D=aMb

(1)

式中，a，b为系数，可通过回归得到。将上式转换为对数函数，则可简化为式(2)所示的线性回归问题

lnE=lna+blnM

(2)

结构地震需求的离散度可表示为

(3)

式中，Mi为第i个地震动峰值；ei为桥梁在第i个地震动作用下的需求峰值；N为地震动总数。

基于上述概率地震需求模型，可获得桥梁的地震易损性曲线。

2 液体黏滞阻尼器

近年来，阻尼器在桥梁工程中广泛使用，用于提高抗震性能、减小结构振动。国内外研究者在大量试验研究的基础上，提出了多种黏滞阻尼器分析计算模型，其中，Maxwell模型能较好地满足一般的黏滞阻尼器，且在有限元软件中易于实现。

在实际工程中，阻尼器一般为非线性阻尼器，即Maxwell模型中阻尼器抗力与速度呈非线性关系

(4)

式中，Fd(t)为阻尼器抗力；K为刚度系数；C为阻尼系数；α为阻尼指数；u1(t)和u2(t)分别为阻尼器和弹簧的位移。

阻尼指数α对阻尼器动力性能的影响较大，随着阻尼指数α的减小，阻尼器的耗能能力增强，阻尼器的滞回曲线愈发饱满。原则上α可以取0.3～1.0的数值，但是参数优化和使用结果都表明，采用阻尼指数为0.3～0.5的非线性黏滞阻尼器效果较好。

3 桥梁易损性分析模型

3.1 工程背景

以一座高速铁路悬臂施工预应力混凝土单线连续梁桥为工程背景，此桥所处场地类型为Ⅰ类，地震动反应谱特征周期为0.35 s。桥跨布置为(32+48+32) m，如图1所示。主梁截面见图2。

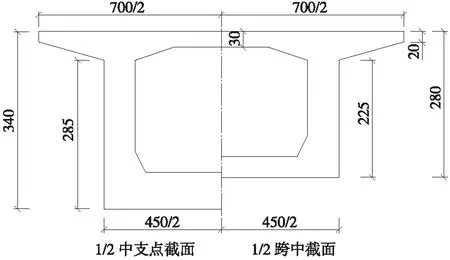
图2 主梁断面(单位：cm)

主梁采用变截面单箱单室箱梁，变截面圆曲线半径为385.508 m，支座处箱梁梁高3.4 m，跨中及边跨梁高为2.8 m；桥墩为圆端形截面，如图3所示。

图3 桥墩截面(单位: cm)

主梁混凝土为C50，桥墩混凝土为C35；承台混凝土为C40，桥墩纵向受力钢筋为HRB400，桥墩箍筋及摩擦桩受力钢筋采用HPB300。主梁采用QZ系列球型支座，每个支点设置2个支座，中支座为12 500 kN级，端支座为4 000 kN级，固定支座位于3号桥墩上。

3.2 有限元模型

建模时，主梁、桥墩、支座和阻尼器分别采用4种不同的单元，如图4所示。

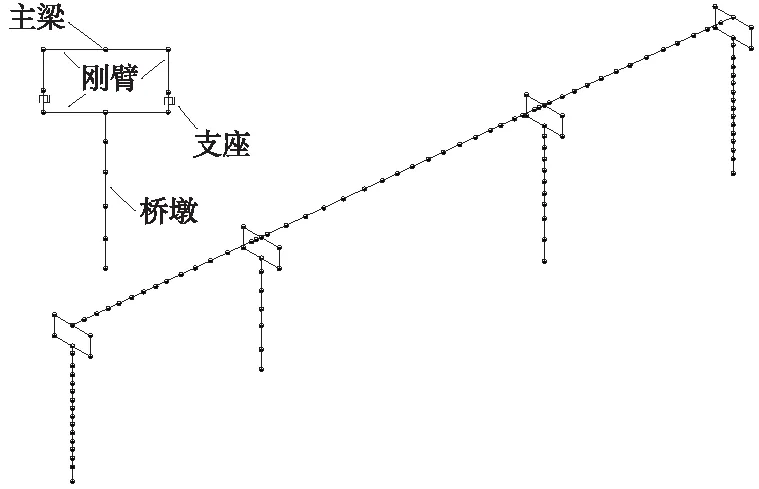
图4 全桥有限元模型

主梁采用OpenSees中的弹性梁柱单元 (Elastic-Element) 对主梁进行模拟，不考虑其非线性因素；桥墩采用OpenSees中非线性梁柱单元 (Nonlinear Beam-Column Elements)对桥墩进行模拟；支座采用OpenSees中零长度单元(Zero-Length Element)对支座进行模拟。

支座应力与应变的关系曲线见图5。

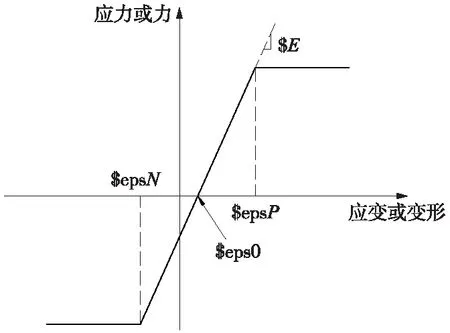
图5 支座应力与应变的关系曲线

图5中，$E为支座刚度，$eps0为初应变，取值为0；$epsP为塑性拉应变，取值为0.002；$epsN为塑性压应变，取值为-0.002。

采用Maxwell Material定义阻尼器材料[20]。模拟阻尼器时将Maxwell材料赋予Two node link element。分别采用Steel01和Concrete01材料模拟钢筋和混凝土，并利用过镇海模型[21]考虑约束混凝土的本构。支座采用零长度单元的材料特性模拟。钢筋的材料本构如图6所示，混凝土及支座的参数分别如表1、表2所示。

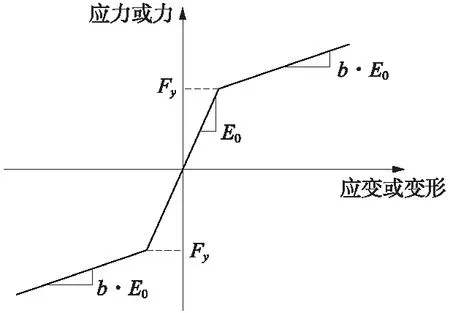
图6 钢筋材料本构

图6中，E0=2×105MPa，Fy=335 MPa，b=1.0×10-5。

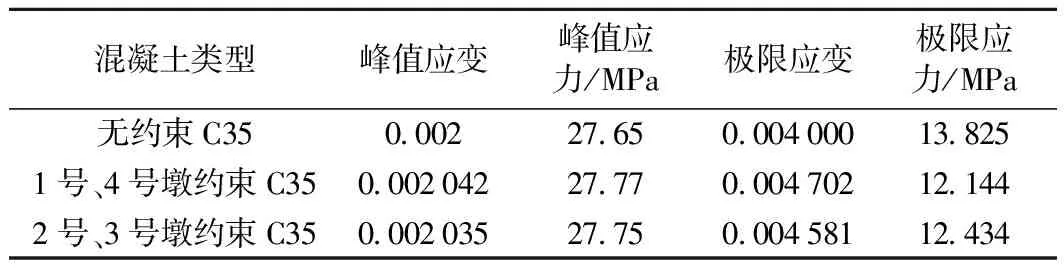
表1 混凝土材料参数

表2 支座参数

3.3 地震动输入

本文采用增量动力分析(IDA)法，综合考虑频谱特性、地震波持续时间和地震波幅值等因素的影响。为保证计算精度，根据表3中的参数从PEER地震动数据库中选取图7所示的20条地震波。

表3 地震动参数

4 损伤状态定义

4.1 桥墩损伤指标

以桥墩墩底曲率作为桥墩工程需求参数EDP，墩底截面的弯矩-曲率曲线如图8所示，损伤指标的定义见表4。

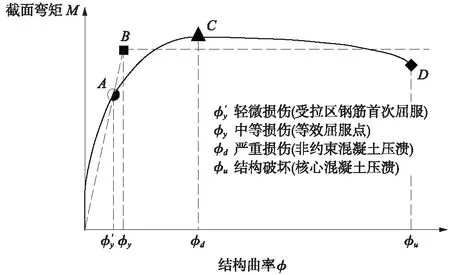
图8 弯矩-曲率曲线

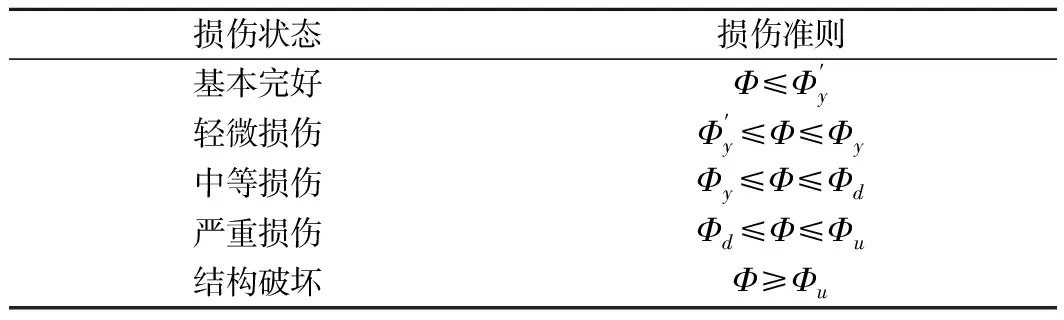
损伤状态损伤准则基本完好Φ≤Φ′y轻微损伤Φ′y ≤Φ≤Φy中等损伤Φy≤Φ≤Φd严重损伤Φd≤Φ≤Φu结构破坏Φ≥Φu

4.2 支座损伤指标

本文中连续梁桥活动支座容许位移为150 mm，根据文献[13]和桥梁球型支座规范，定义活动支座损伤状态时，支座损伤指标定义见表5。

表5 支座损伤指标定义

注：D为地震作用下支座的相对位移。

5 概率地震需求模型

有限元模型建立后，利用选取的20条地震波对结构进行非线性时程分析。计算时采用IDA方法，将每条地震波分为10级，通过调幅使PGA增量为0.1g，从而得到200个计算工况。

通过回归分析，可得到地震需求和地震动强度的关系

(5)

式中，u为结构地震需求；A和B为回归方程系数。

同样可得到需求对数标准差与PGA间的函数关系

(6)

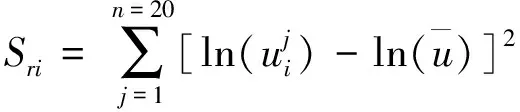
(7)

式中，βi为第i组数据的对数标准差；Sri为第i组各数据点对数值与对数平均值差值的平方和。

对多次拟合的效果进行比较，最终决定墩底曲率和支座位移地震需求的对数标准差采用式(8)、式(9)进行拟合。

βφ=Aφ(PGA)2+Bφ(PGA)+Cφ

(8)

βd=Ad(PGA)3+Bd(PGA)2+Cd(PGA)+Dd

(9)

式中，βφ和βd分别为墩底曲率和支座位移的标准差；Aφ、Ad、Bφ、Bd、Cd、Cφ和Dd均为回归系数。

通过对桥梁纵向地震响应数值分析，发现纵向地震作用下固定墩(3号墩)曲率远大于其他桥墩；3个活动支座位移基本一致，但4号墩活动支座纵向位移值是其中最大的。所以，将固定墩和4号墩活动支座作为本次易损性分析的研究对象。

6 易损性分析

6.1 阻尼系数的影响

为了研究阻尼系数对高速铁路连续梁桥地震易损性的影响，保持阻尼指数不变，计算了阻尼系数为1 000，2 000，3 000，4 000，5 000，6 000 kN·s/m时的损伤概率。结果表明：各类损伤的概率随阻尼系数变化趋势相同，限于篇幅仅给出桥墩和支座发生轻微损伤和严重损伤时的易损性曲面，如图9、图10所示。

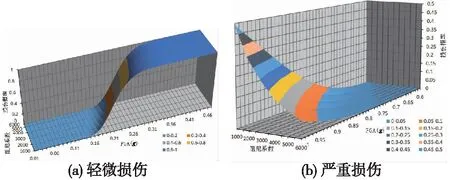
图9 阻尼系数变化的桥墩易损性曲面

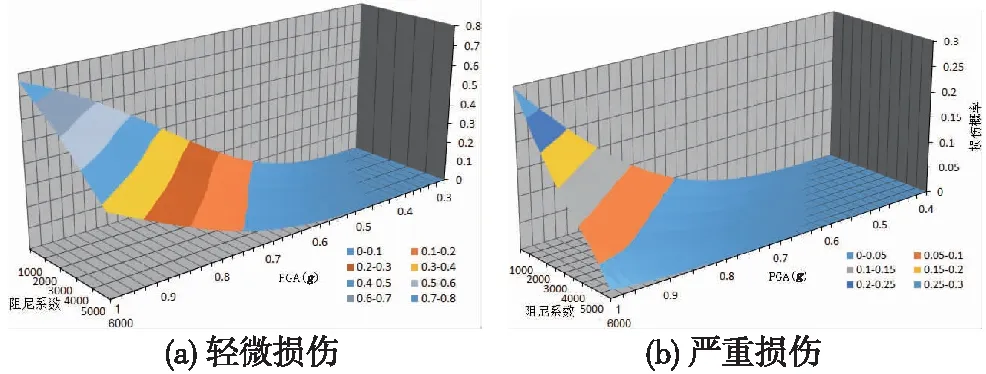
图10 阻尼系数变化的支座易损性曲面

由图9可知：随着阻尼系数的增大，同等地震动强度下，桥墩发生轻微损伤的概率略有减小。PGA为0.19g时，轻微损伤概率的下降速度最快，平均减幅为4.67%；同等地震动强度下，桥墩发生严重损伤的概率明显下降。PGA为0.77g时，轻微损伤概率的下降速度最快，平均减幅为44.13%。

由图10可知：随着阻尼系数的增大，同等地震动强度下，支座发生各类损伤的概率都有明显下降。其中，PGA为0.54g时，轻微损伤概率的降低速度最快，平均减幅为38.79%，PGA为0.74g时，严重损伤概率的降低速度最快，平均减幅为51.51%。

综上，阻尼系数的提高使各墩受力更为协调，固定墩曲率减小，活动支座位移减小，固定墩和活动支座在地震作用下发生各类损伤的概率都有所下降，桥梁的抗震性能提高。

6.2 阻尼指数的影响

为了研究阻尼指数对高速铁路连续梁桥地震易损性的影响，保持阻尼系数不变，计算了阻尼指数为0.2、0.3、0.4、0.5、0.6、0.7时的损伤概率。同样，仅给出桥墩和支座发生轻微损伤和严重损伤时的易损性曲面，如图11、图12所示。

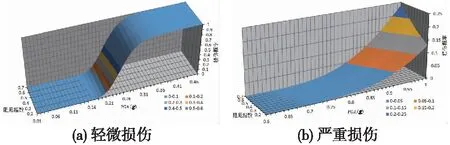
图11 阻尼指数变化的桥墩易损性曲面

图12 阻尼指数变化的支座易损性曲面

由图11可知：随着阻尼指数的增大，同等地震动强度下，桥墩发生轻微损伤的概率略微增大。PGA为0.21g时，轻微损伤概率的增长速度最快，平均增幅为4.82%；同等地震动强度下，桥墩发生严重损伤的概率明显增大。PGA为0.71g时，严重损伤概率的增长速度最快，平均增幅为21.37%。

由图12可知：随着阻尼指数的增大，同等地震动强度下，支座发生各类损伤的概率都有明显增大。其中，PGA为0.58g时，轻微损伤概率的增长速度最快，平均增幅为17.99%，PGA为0.72g时，严重损伤概率的增长速度最快，平均增幅为25.39%。

综上，阻尼指数的降低使各墩受力更为协调，固定墩曲率小幅减小，活动支座位移小幅减小，固定墩和活动支座在地震作用下发生各类损伤的概率都有所下降，桥梁的抗震性能提高。

7 结论

通过开源程序OpenSees，以一座(32+48+32) m连续梁桥为工程背景，建立了高速铁路连续梁桥在地震作用下的动力响应的数值模型，研究了阻尼系数及阻尼指数对桥梁地震易损性的影响，根据本文数值结果，得出如下结论。

(1)地震作用下，相对于未设置阻尼器工况，桥梁的受力更为合理，桥墩和支座的损伤概率也有较大的下降，说明阻尼器提高桥梁的抗震性能，减小了地震作用下的损伤概率。

(2)阻尼系数的提高与阻尼指数的降低均使各墩受力更为协调，固定墩曲率减小，活动支座位移减小，固定墩和活动支座在地震作用下发生各类损伤的概率都有所下降，桥梁的抗震性能提高。

(3)工程中可通过在高速铁路桥梁桥墩及支座位置设置阻尼器，并合理调整阻尼器参数来提高桥梁的抗震性能及改善桥梁的地震易损性。