复杂地质条件下煤体-充填体协同控制技术

李 柱，谢 锋

（1.重庆水利电力职业技术学院，重庆 402160；2.重庆市武隆交通委员会，重庆 408500）

近年来，浅部煤炭资源接近枯竭，因此不得不延伸至深井开采[1-2]。为了减少开采造成的煤炭资源浪费和提高回采准备巷道成型效率，提出了采用充填的方式来解决目前遇到的一系列问题[3-4]。在深部矿井中进行沿空掘巷往往比沿空留巷的维护要简单些，但其所处力学环境仍比宽煤柱护巷条件下复杂的多[5-7]。虽然我国对沿空掘巷的研究已经很多，也相应的对护巷合理煤柱宽度的留设提出了不同的计算方法，但其应用广泛性还有待进一步验证。

1 工程地质概况

冀中能源宣东二矿Ⅲ3302工作面埋深800 m，上临Ⅲ3303工作面，左为三采区运输上山。为了保证正常采掘接替，准备在不改变Ⅲ3302工作面通风方式的条件下，采用巷内充填沿空掘巷方式，以保证掘进速度。按照有关规定，煤层瓦斯压力小于0.74 MPa时或者瓦斯含量小于8 m3/t时，可只进行区域瓦斯验证，这样可极大加快掘进速度。

在高瓦斯矿井实施巷内充填沿空掘巷的目的，就是找到合适的掘巷范围，即可加快掘进速度，解决采掘接替问题，又不违反国家相关的安全规程的规定。在寻找合适沿空掘巷范围的过程中，防止煤柱过窄导致完全变形破坏，巷内充填沿空掘巷示意图如图1。

2 巷内充填工艺

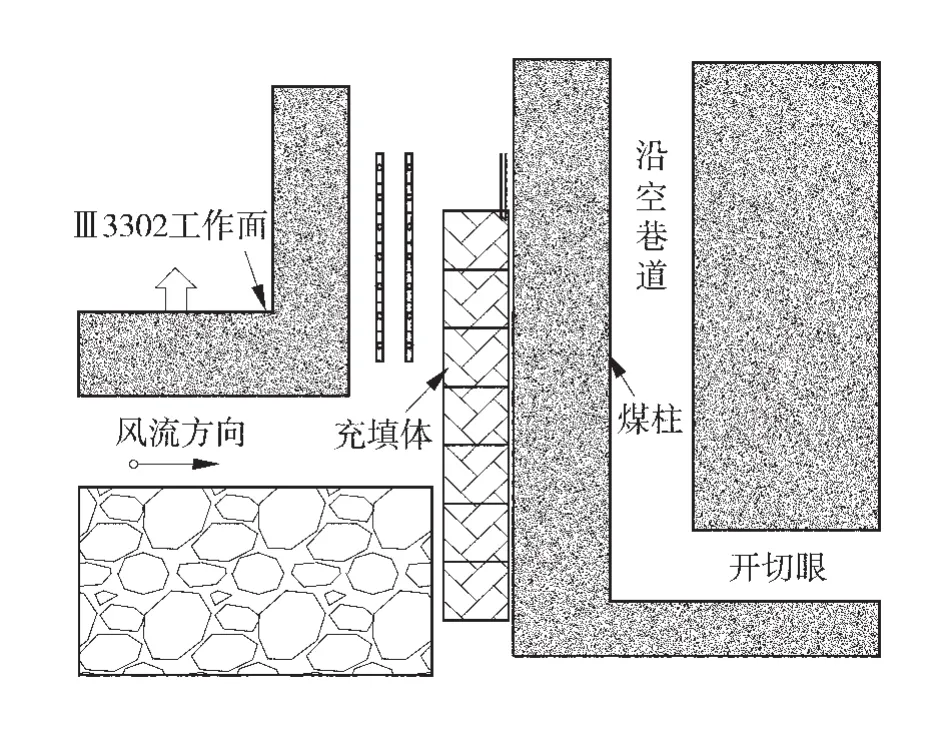
图1 巷内充填沿空掘巷示意图

在不改变通风方式、保证工作面正常通风的前提下，充填进度要超前于工作面推进进度。为保证通风断面，需要增加巷道的宽度至6 m，由于超宽巷道的顶板维护困难，因此为了防止顶板垮落，须用双排单体液压支柱配铰接顶梁进行提前支护。充填体超前充填的进度，可以根据工作面的推进速度V1（与充填速度相同）和切顶所需充填体的强度p共同确定。根据充填体强度发展曲线，可知切顶强度p所对应的充填体养护龄期为D，X为基本顶的极限跨距，则充填体超前工作面距离为Y=D×V1-X。根据宣东二矿Ⅲ3302工作面现场工程地质条件，可以计算出充填体需要超前工作面的充填距离大于45 m。充填体宽度为3 m，约占巷道宽度的1/2。为了保证巷道的稳定性，除了采用锚杆、锚索联合支护外，利用单体液压支柱对巷道进行加强支护，控制巷道的变形量。其巷道内充填时的剖面图如图2。

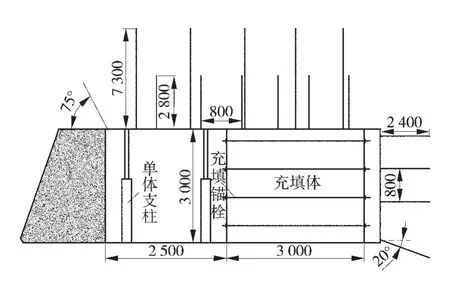
图2 巷内充填剖面示意图

根据宣东二号煤矿Ⅲ3302工作面的实际情况，安排在每天的八点检修班对工作面的巷道进行充填，进行巷内充填的工艺流程如图3。

3 煤体-充填体力学关系分析

3.1 煤体-充填体接触面力学分析

由于煤体-充填是1个长度远远大于宽度的柱形体，可简化为平面问题进行分析[8]，煤体-充填体平面结构简图如图4。

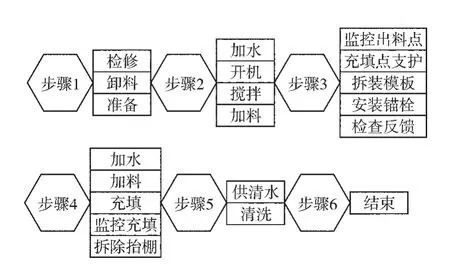
图3 充填工艺流程示意图

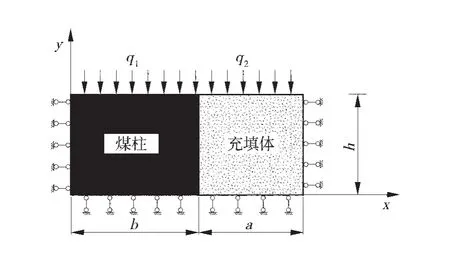
图4 煤体-充填体平面结构简图

煤柱左侧受到锚杆的约束，充填体的右侧同样受到了预应力结构的横向约束，两边为水平简支约束，煤柱-充填体的上部与顶板的接触面受到顶板的压力以及顶、底板接触面的摩擦力限制了煤柱-充填体的水平位移。煤柱-充填体上覆岩层的质量可以简化为均布载荷q。窄煤柱的宽度为b，充填体宽度为a，煤层厚度为m。煤柱体所承受的载荷为q1，充填体所承受的载荷为q2。在覆岩作用下，煤柱体和充填体之间产生了共同向下的位移，则煤柱体与充填体所承受的平均压力q1、q2可分别表示为：

式中：E1、E2为煤柱体和充填体的弹性模量。

同时由于煤柱体和充填体处于平衡状态，根据静力平衡条件可知：

由于煤柱体和充填体共同承担上覆岩层的载荷，当充填体承受载荷较大时，煤柱所承受的载荷相对就会变小，稳定性就会越好。它们之间的载荷也可以表示为：

式中：ρ为覆岩平均密度；H为埋藏浓度。

式中：μ1、μ2分别为煤柱体的泊松比、充填体的泊松比。

可以看出，充填体的弹性模量和泊松比越大，其所能够承受的载荷越大，抵抗变形的能力也就越强。根据胡克定律可以得出煤柱体与充填体之间的相互作用力F0的表达式为：

3.2 煤体-充填体两帮力学模型

将煤体-充填体看成一个整体，对其两帮进行受力分析，煤体-充填体力学模型简图如图5。在其煤柱一侧煤帮主要约束力来自于巷道锚杆的支护阻力ps，而对于充填体一侧主要受力来自采空区垮落矸石对充填体形成的侧向挤压力Fz。煤体-充填体左右两侧横向受力的差异性由煤柱与顶底板的剪切应力和充填体与顶底板的摩擦阻力来进行平衡。

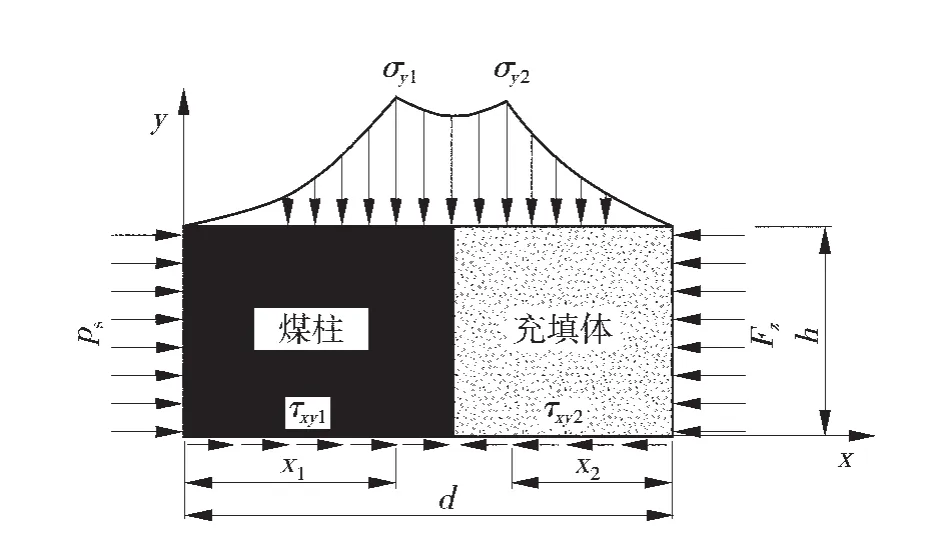
图5 煤体-充填体力学模型简图

其中ps、Fz分别为煤柱左侧的锚杆对煤帮的约束力与采空区矸石对充填体的侧向挤压力；τxy为煤柱对于煤层巷道顶底板的剪切应力；f为充填体与顶底板之间的摩擦阻力；x1、x2分别为煤柱与充填体的应力极限平衡区宽度；σy1、σy2分别是煤柱与充填体的支承压力峰值也即极限强度。其中煤柱的受力模型如图6[9-10]。

对该模型进行求解，其中σy1＝KρgH，K为煤体的应力集中系数，C0、φ0分别为煤体的黏聚力和内摩擦角。利用沿空掘巷实体煤帮应力极限平衡区的计算公式可以推导出模型中x1的表达式：

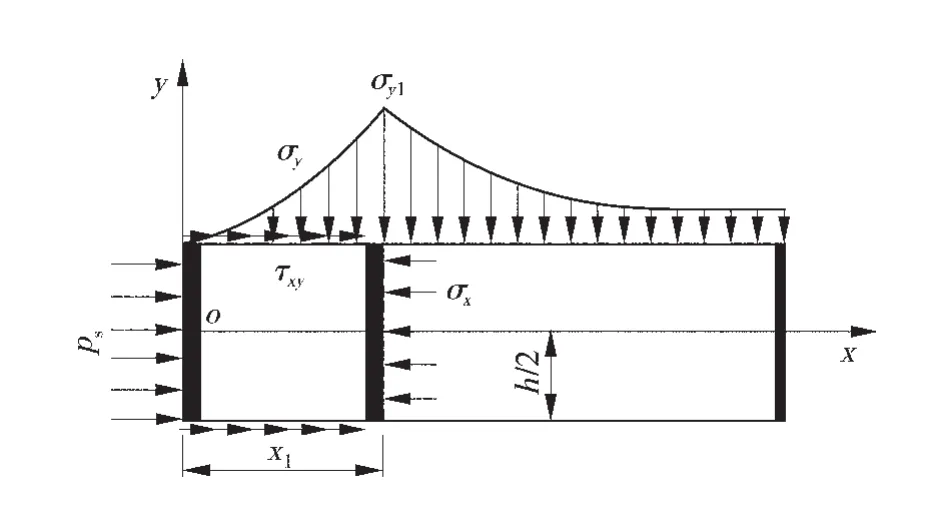
图6 煤柱受力模型简图

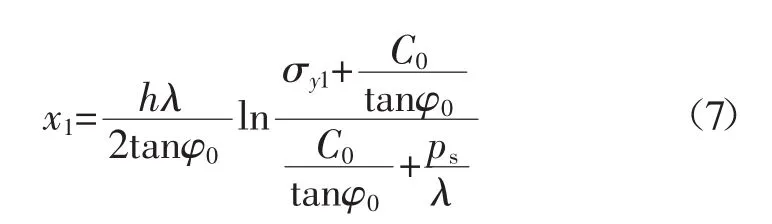
式中：λ为侧压系数；h为巷道高度。

对于沿空掘巷巷帮煤柱应力极限平衡区内任意一点的应力表达式为：

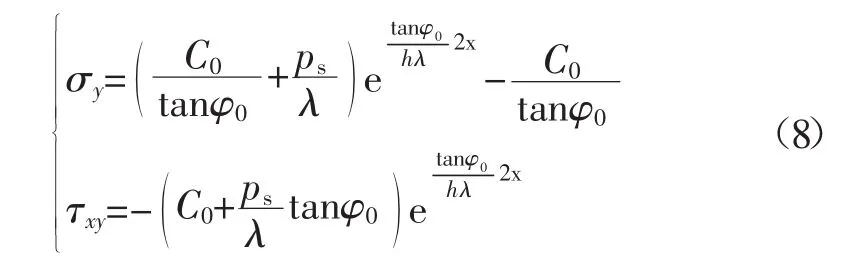
假设沿空掘巷充填体的应力集中系数为Kc，富裕系数为A；则对于充填体在水平方向的应力σxc的表达式为：

充填体的受力模型如图7。

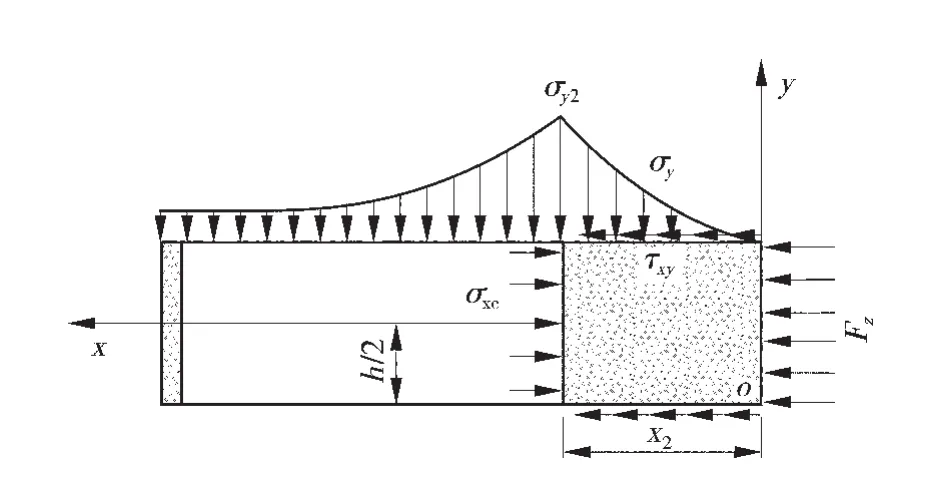
图7 充填体受力模型简图

对该模型进行求解，利用应力极限平衡区的计算公式可以得出充填体的应力极限平衡区域的x2的表达式：

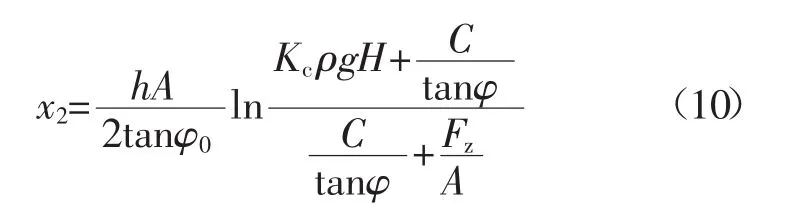
式中：C、φ分别为充填材料的黏聚力和内摩擦角。

充填体采空区侧的极限平衡区内任意一点的应力表达式：

3.3 煤体-充填体的影响因素分析

Ⅲ3煤层埋深H=800 m，煤体的黏聚力C0=2.5 MPa，巷道高度h=3 m，应力集中系数K=2，内摩擦角 φ0=30°，侧压系数 λ=1.8，覆岩的平均密度 ρ=2.2 t/m3，煤体的弹性模量E=2 400 MPa，其煤层的性质、埋深、巷道的设计宽度都已固定，因此研究影响煤体-充填体的塑性区宽度影响因素时，只考虑支护阻力、充填体强度等对煤体-充填体的塑性区宽度的影响。不同充填体强度的设置参数见表1。

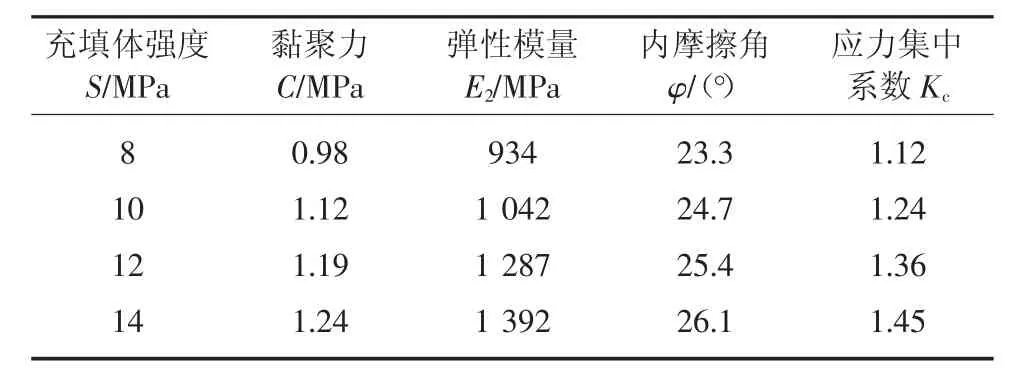
表1 不同强度充填体的力学参数

根据式（7）和式（10）可分别计算出充填体侧不同强度大小和煤体侧不同强度大小时塑性区宽度的变化情况（图8）。

图8 煤体-充填体两侧塑性区宽度分布规律

由图8（a）可知，随着充填体强度的上升，塑性区的宽度也出现了明显的下降。可见通过改善充填体自身强度可以在一定程度上降低塑性区宽度，增加支撑力，改善沿空掘巷巷道的稳定性。由图8（b）可知，煤柱侧在支护强度改变时，塑性区宽度也随之发生改变，支护强度越大越有利于巷道围岩的稳定性，因此在进行沿空掘巷时，合理设计巷道支护方案，对控制巷道围岩的变形破坏有一定的作用。

基于Kastner公式，考虑煤层瓦斯影响得到高瓦斯煤层巷道的围岩塑性区半径R的计算如式（1）。

式中：r1为巷道半径；pi为平均支护阻力；p0为瓦斯压力。

针对宣东二号煤矿沿空掘巷工作面煤层参数，工作面埋深800 m，覆岩平均密度为2.5 t/m3，巷道半径r1为2 m，瓦斯压力p0为2 MPa，平均支护阻力pi为1 MPa，煤体黏聚力C为1.5 MPa，内摩擦角φ为30°。为了简化理论计算，假设巷道处于静水应力场，巷道塑性区与弹性区交界的边缘应力可表示为ρgH+p0。

塑性区半径与瓦斯压力的关系如图9。由图9可知，随着瓦斯压力越大，塑性区半径范围也随之增大，因此在工程实践中进行沿空掘巷时，需要对煤层内瓦斯压力进行监测与分析，在确定沿空掘巷煤柱留设宽度时，应该对瓦斯压力对煤体所产生的影响进行综合考虑。

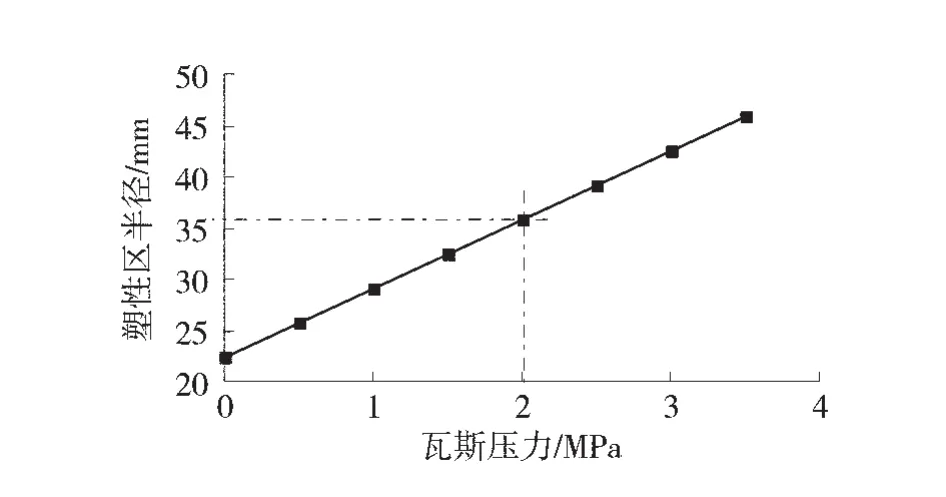
图9 塑性区半径与瓦斯压力的关系

根据Ⅲ3煤层地质情况，并基于式（7）和式（10）可计算求解出煤体-充填体协同护巷时巷道侧煤柱的塑性区宽度x1=1.82 m，采空侧充填体的塑性区宽度x2=2.11 m，瓦斯压力影响塑性区半径R=0.36 m。考到到煤体-充填体的稳定性，可按照（x1＋x2＋R）的30%～50%确定中间弹性核区的宽度x3，在此按照40%确定为x3=1.72 m，因此可以确定煤体-充填体的总宽度为W=6.01 m。

4 工程应用

为了检验支护效果，在超前工作面60 m位置处设置矿压监测点，对巷道围岩变形情况进行监测。相邻工作面回采期间巷道围岩变形情况如图10。由图10中监测数据可知：工作面回采期间，巷道顶、底板移近量分别为380 mm和315 mm，煤柱帮和实体煤帮移近量分别为352 mm和338 mm，围岩整体变形在可控范围内，没有发生失稳现象，说明煤体-充填体协同护巷方案达到了预期的效果。

图10 相邻工作面回采期间巷道围岩变形情况

5 结论

1）根据宣东二矿Ⅲ3302工作面现场工程地质条件，计算出充填体超前工作面的充填距离≥45 m，充填体的宽度为3 m，约占巷道宽度的1/2。

2）通过建立煤体-充填体力学模型对其进行计算分析，得知通过改善充填体自身强度和支护强度有利于巷道围岩的稳定性，并根据Ⅲ3煤层地质情况可知受瓦斯压力影响下煤体-充填体的最优宽度为6.01 m。

3）现场矿压观测结果表明，邻近工作面回采过程中，煤体-充填体协同护巷下巷道顶、底板移近量分别为380 mm和315 mm，煤柱帮和实体煤帮移近量分别为352 mm和338 mm，围岩整体变形在可控范围内。