采用PageRank和节点聚类系数的标签传播重叠社区发现算法*

马 健，刘 峰，李红辉，樊建平

(北京交通大学 计算机与信息技术学院， 北京 100044)

社区结构(community)是复杂网络所呈现的重要特征之一，从某种意义上说，整个网络由若干社区构成，具有社区内部节点之间连接比较密集，不同社区节点之间连接比较稀疏的特点[1]。复杂网络社区发现问题就是要揭示出复杂网络中存在的各个社区。从社区之间是否重叠的角度来看,社区结构是可以重叠的。例如人类社会关系网中的一个人可以拥有多个朋友圈，Internet中，一个路由器可以连接不同的局域网，在神经网络中，一个神经元可以属于不同的神经系统。

重叠社区的发现算法可以分为：基于派系过滤算法(Clique Percolation Method, CPM)的重叠社区发现算法，它将网络看作是完全连通子图(clique)的集合[2-3]。基于优化函数的重叠社区发现算法[4-5]，其中，Lancichinetti等[4]提出了LFM (Local Fitness Method)算法，该算法既可以发现层次社区又可以发现重叠社区。基于边的重叠社区发现算法[6-7]，基于标签传播的社区发现算法，Gregory等[8]提出了重叠社区发现算法(Community Overlap PRopagation Algorithm， COPRA)。Wu等[9]提出了基于均衡多标签传播的重叠社团发现算法(Balanced Multi-Label Propagation Algorithm, BMLPA)算法，定义了粗糙核的概念对节点的标签进行初始化，通过更改标签更新时的参数改进算法。张昌理等[10]提出了多标签传播重叠社区发现算法COPRA-EP，算法利用节点信息熵和节点的局部相关性进行研究。Cui等[11]从网络中发现所有最大子图，然后通过两个相邻最大子图的聚类系数来合并它们。Mohan等[12]提出了一个分布式和可扩展的模型来最大化信息的扩散，通过将图划分为社区并寻找每个社区中有影响的节点来检测社区，模型使用PageRank算法在每个社区中寻找有影响的节点。孙道平等[13]提出了一种算法计算网络节点的聚类系数，并选择具有最大聚类系数的节点来更新其在传播过程中的标签。Chen等[14]提出了基于节点层次和标签传播增益的重叠社区发现算法，算法提出了新的多标签更新规则，设计节点之间标签传播增益得到重叠社区。Xie等[15]提出了一种SLPA算法。

本文提出了一种基于PageRank和节点聚类系数的重叠标签传播算法(Community Overlap PRopagation Algorithm based on PageRank and Clustering coefficient,COPRAPC)。该算法在传播节点的社区标签时按节点影响力的大小进行排序，并且根据节点的聚类系数决定传播的阈值，最后通过一系列实验进行验证，实验结果表明所提出的重叠社区检测算法是可行且有效的。

1 COPRA算法

1.1 COPRA算法描述

COPRA算法(见图1)在标签传播算法(Label Propagation Algorithm， LPA)算法基础上改进解决重叠社区发现的问题，每个节点拥有多个标签(label)和隶属度(belonging coefficients)，所有隶属度的和等于1，标签采用同步更新的方式，用每个节点的邻居节点的标签更新该节点，属于相同社区标签的隶属度相加并标准化，如式(1)所示，隶属度小于1/v的标签将从标签列表中删除，阈值v用来控制一个节点所属的社区数。COPRA标签传播算法的时间复杂度为O(vmlog(vm/n))，当v取较小值时，整个算法复杂度为线性时间复杂度。

(1)

(a) 第1次迭代(a) Iteration 1 (b) 第2次迭代(b) Iteration 2

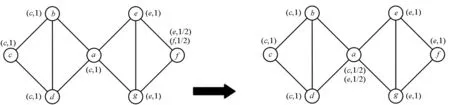
(c) 第3次迭代(c) Iteration 3 (d) 第4次迭代(d) Iteration 4图1 COPRA 算法Fig.1 COPRA algorithm

1.2 评价函数

Qov是Nicosia等将Q函数扩展提出的能够评价重叠社区的评价函数[16]。Qov越大，社区结构越明显。

(2)

其中，

δ(Ci,Cj,C)=F(αi,c,αj,c)

f(x)=2px-p,p=30

EQ是评估重叠社区的另一个度量标准，EQ值越大，社区的结构越明显。表达式如下[3]：

(3)

Lancichinetti等将标准互信息(Normalized Mutual Information, NMI)扩展为能够评价重叠社区的一种评价指标[2]。

(4)

2 COPRAPC算法

2.1 算法思想及描述

COPRAPC算法和其他重叠标签传播算法的不同之处在于算法采用不同的阈值来限制每个节点拥有最多标签的数量值，每个节点可能出现在多个社区中，社区边缘节点拥有较小聚类系数一般是重叠节点，社区内部节点拥有大聚类系数往往是非重叠节点，社区边缘节点比社区内部属于更多的社区。小的聚类系数做阈值可以保留节点更多的标签，而大的聚类系数可以删除节点更多的标签，重叠的节点可以比非重叠的节点保留更多的标签。此外，复杂网络的小世界特性决定了节点具有较高聚类系数，从而避免了传播过程中节点的标签对过多的问题。

COPRAPC算法采用同步更新策略。对于同步策略来说，可以比异步方式提供更稳定的结果，但是同步方案需要更多的迭代次数。

在COPRA算法中，每个节点都有一个标签，在传播过程中，节点标签在没有特定序列的情况下更新。这种随机策略导致运行结果不稳定。如图1(c)中所示的COPRA算法中，在这次迭代之后，节点a、b、c和d已经形成了一个社区。如果算法选择节点e或g，用节点a的标签替换它的标签，然后更新节点f的标签，那么，所有节点都使用c作为它们的标签，所有的节点将被划分为一个社区，结果导致整个网络在一个社区中。如果首先更新节点f的标签，将得到正确的分区结果。

图2显示了两个非重叠社区C1和C2迭代之后，如果节点d,e,f被分配到社区C2，此时更新节点g，将得到正确的社区分区，但如果更新节点b或c的标签并选择节点d和e作为它的标签，所有节点将拥有相同的标签，结果是所有节点被划分到相同的社区。

图2 COPRAPC算法实例Fig.2 Example of COPRAPC propagation

上述两个例子说明COPRA算法对节点更新序列很敏感，不是所有这些节点都具有相同的优先级。在社区之间的节点的影响力总是比社区内部的节点要低。PageRank值反映了这个特性，本文使用排名方法PageRank算法[17]对节点进行排序。首先，将无向图转换为有向图，将无向图中的边转换为具有两个相反方向的弧。PageRank的较小值往往位于社区中心，PageRank值小的节点优先于PageRank值较大的节点，即

(5)

其中，α参数为0.85，v′是节点v的邻居，degress(v′)为节点v′的度。

节点的PageRank值:PR(a)=0.146 6,PR(b)=0.147 6,PR(c)=0.147 6,PR(d)=0.152 0,PR(e)=0.152 0,PR(f)=0.107 6,PR(g)=0.146 6。节点在以下序列中更新它们的标签：f、a、g、b、c、d和e，可以很容易地得到正确的结果。

2.2 修改传播门限参数

在COPRA算法中，使用标签列表(c,b)表示每个节点拥有的标签，其中c表示一个标签(label)，b表示隶属度。如果b<1/v，从节点标签列表中删除(c,b)。在重叠的社区中，每个节点可能属于多个社区。参数v控制重叠的社区数目。也就是说，参数v限制节点所属的社区最大数量。如果v太大，则可能导致网络中节点的标签对过少，节点容易被划分到一个社区，如果v太小，则会导致网络中节点的标签对过多。参数v的选择能够影响标签传播算法重叠社区发现的准确性，由于每个节点所属社区数目是不相同的，因此，本文提出了一种新的标签传播算法，根据不同的节点选择不同的参数。

在网络中，节点vi的邻居节点之间实际存在的边数和可能存在最多边数的比值为节点vi的聚类系数[18]，每个节点vi邻居节点之间可能最多是ki×(ki-1)/2条边。节点vi的聚类系数如式(6)所示。

(6)

其中，Ei表示连接到节点vi的每个相邻节点的边数，ki表示节点vi所有相邻节点的个数。聚类系数Ci总是在0至1之间。

COPRAPC算法允许社区重叠，每个节点可能出现在多个社区中。社区边缘节点总是重叠节点，社区中间节点往往是非重叠节点，重叠节点聚类系数往往小于非重叠节点，重叠节点的聚类系数较小通常处在社区的边缘，非重叠社区的节点都在社区中间聚类系数较大，换句话说，一个社区边缘节点拥有小聚类系数可能比社区中间拥有大聚类系数属于更多的社区。更高的阈值可以删除节点更多的标签，重叠的节点可以比非重叠的节点保留更多的标签。

v是一个与节点无关的参数。相反，聚类系数参数是一个与节点相关的参数，算法设置参数μ，当节点的聚类系数大于μ，阈值设为节点的聚类系数，反之，使用先前的值1/v。这样做的目的是聚类系数大的节点一般在社区内部，往往不是重叠节点，这样的节点设置的门限高，可以去除较多的标签，而聚类系数小的节点一般在社区的边缘，容易成为重叠节点，设置的门限较低可以增加标签的数量。但对于聚类系数非常小的节点，阈值过低容易产生空的标签集合，这时就用原来的门限值1/v。

COPRAPC算法描述：

1)初始时，给每个节点赋予唯一的社区标签(cx,1)。

2)对网络中的节点按其PageRank值排序。

3)每个节点x通过最大邻居的数量来更新它的标签。属于相同社区的标签的隶属度相加并标准化，为了避免最后所有节点都划分到同一个社区，COPRAPC算法使用节点的聚类系数来限制每个节点拥有最多标签的数量值。如果节点的聚类系数小于参数μ，仍然使用原来的1/v，如果一个节点的所有标签隶属度都小于传播参数，那么随机选择一个最大值邻居的标签作为该节点的标签。最后，当每个标签包含的节点数不变，算法迭代结束，否则，重复步骤3。

4)将所有标签相同的节点划分为同一个社区。

5)将得到的社区进行删除其他社区的子集，不相连的社区分裂成更小的社区。

COPRAPC算法的形式化语言如算法1和算法2所示。

算法1 计算节点的聚类系数

算法2 COPRAPC算法

2.3 复杂度分析

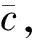
1)初始化标签的时间复杂度为O(n)。

2)设计算单个节点PageRank值的迭代次数为t，矩阵相乘时间复杂度为O(n2)，所以计算单个节点的PageRank值的时间复杂度为O(n2×t)，计算网络中所有节点的PageRank值的时间复杂度为O(n3×t)，根据节点排序更新序列的时间复杂度为O(n)。

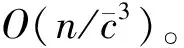
3 实验分析

为了验证所提出的COPRAPC算法，将它与几个重叠社区的发现算法进行比较:CPM, LFM, BMLPA和COPRA。

Lancichinetti的NMI已被广泛用于发现重叠社区，因此本文在实验中采用扩展的NMI作为度量标准。实验独立运行COPRA算法20次实验数据，得到平均结果。COPRAPC算法由于标签选择的随机性，本文独立运行了10次数据集取平均结果。CPM算法，k=4, BMPLA 算法，p=0.75。

3.1 LFR基准网络

LFR基准网络，该网络由Lancichinetti等提出，是一类更接近真实网络的人工网络，该网络节点及社区模型度呈幂律分布，具有真实世界的网络特性。N表示节点数目，d表示节点平均度数，k表示节点最大度，minc表示最小社区规模，maxc表示最大社区规模，t1表示节点度的幂率分布指数，t2表示社区规模的幂率分布指数，混合参数mu，on表示重叠节点的个数，om表示重叠节点所属的社区个数，表1和表2为LFR基准网络的参数。表1中的社区分别表示稠密小社区(Dense Small, DS)，稠密大社区(Dense Large, DL)，稀疏小社区(Sparse Small, SS)，稀疏大社区(Sparse Large, SL)。表1中实验节点的聚类系数都较大，因此设置μ=0。

表1 重叠社区的LFR基准网络参数

表2 非重叠社区的LFR基准网络参数

图3显示该算法在实验中表现良好。随着参数on的增大，重叠节点的数量越来越多。COPRAPC性能较优。

(a) DS网络的NMI值(a) NMI identified by DS networks

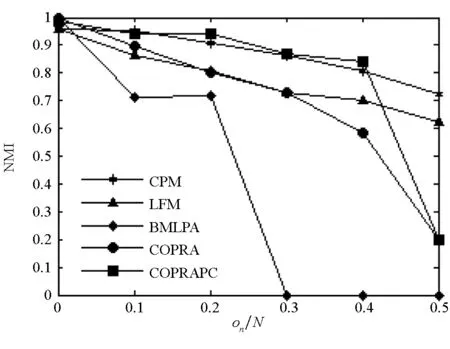
(b) SS网络的NMI值(b) NMI identified by SS networks

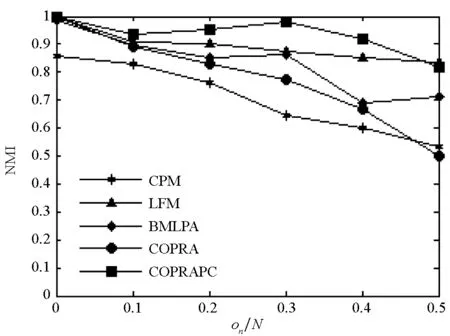
(c) DL网络的NMI值(c) NMI identified by DL networks

(d) SL网络的NMI值(d) NMI identified by SL networks图3 CPM, LFM, COPRA, BMLPA and COPRAPC算法的NMI对比结果Fig.3 The NMI identified by CPM, LFM, COPRA, BMLPA and COPRAPC

表2中的实验数据集节点的聚类系数较小，因此设μ=0.1。

上述是一个具有非重叠节点的社区网络。随着参数mu的增加，当值mu=0.4时社区的结构变得模糊，图4显示该算法在这些网络中表现良好。

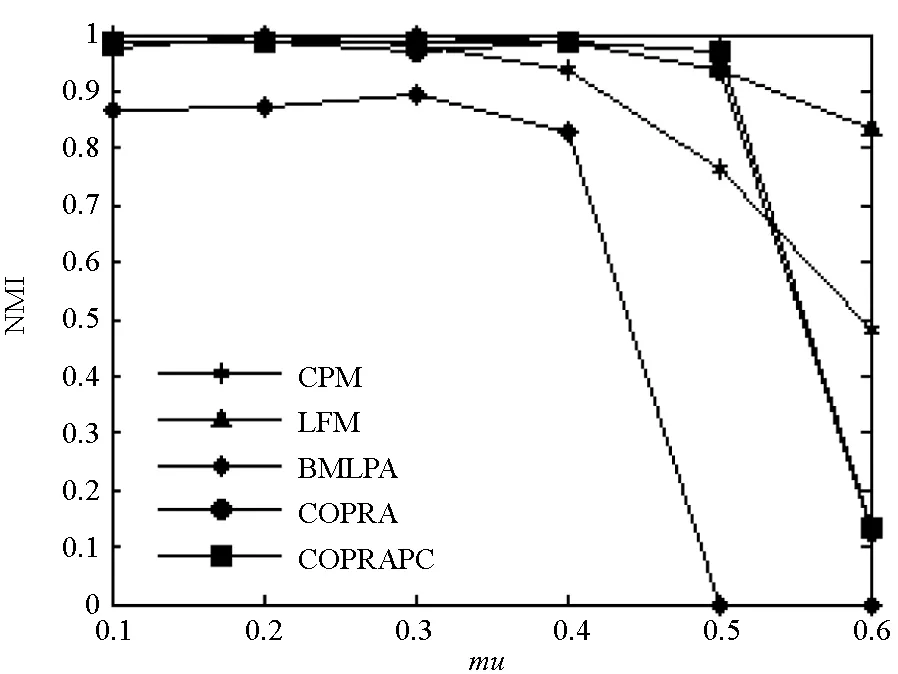
(a) Network a的NMI值(a) NMI identified by network a

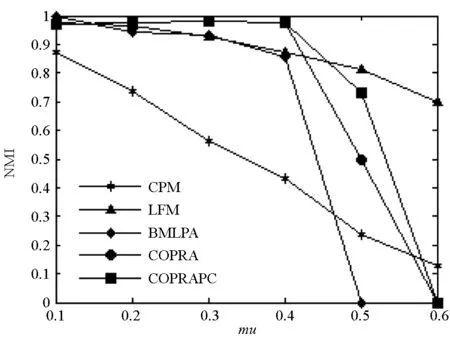
(b) Network b的NMI值(b) NMI identified by network b图4 CPM, LFM, COPRA, BMLPA and COPRAPC算法的NMI对比结果Fig.4 The NMI identified by CPM, LFM, COPRA, BMLPA and COPRAPC

3.2 真实世界网络

本文在几个真实世界复杂网络上对算法进行测试，实验采用的数据分别是：Newman提供的空手道俱乐部网络(Zachary′s club network)、海豚网络(dolphin social network)、美国大学足球联盟网络 (American college football)、爵士音乐网络(Jazz music)、政治书籍(political books)和邮件网络(the E-mail network of human interactions)。表3为实验用到的真实网络参数。实验中，设置参数μ=0.2。表4和表5分别给出了解情况种算法在个真实世界网络中的Qov和EQ值。

表3 真实世界网络参数

在基准网络和真实网络的实验中，算法的社区发现结果是稳定的，基于此思想的算法相比其他标签传播重叠社区发现算法有明显的提高，和其他重叠算法相比也有较好的挖掘结果，这也说明了基于PageRank和节点聚类系数的思路是可行的。

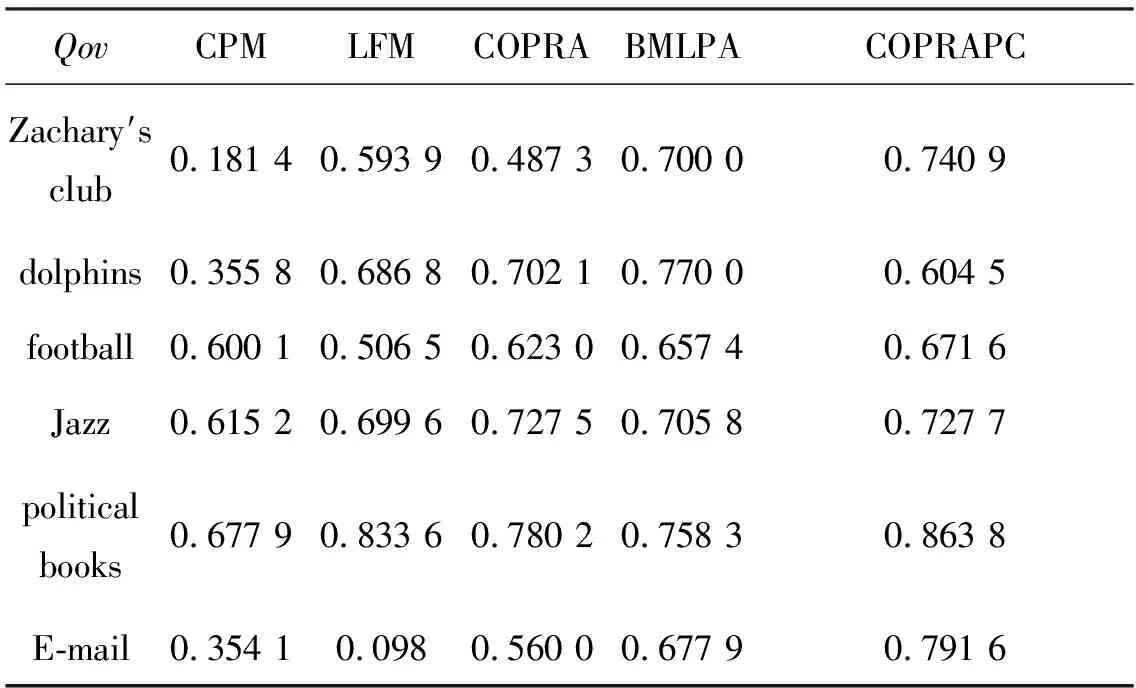
表4 CPM LFM, COPRA, BMLPA and COPRAPC算法的Qov值Tab.4 The Qov values identified by CPM, LFM, COPRA, and COPRAPC

表5 CPM, LFM, COPRA, BMLPA and COPRAC算法的EQ值Tab.5 The EQ values identified by CPM, LFM, COPRA, and COPRAPC

3.3 算法效率比较

改变LFR基准程序的参数，可以得到不同规模的人工网络,在这些网络上分别运行社区发现算法,可以得到算法运行时间的一般规律,从而能知道各个算法在效率上的差异。本节使用的LFR程序参数N=1000～10 000,k=20,kmax=50,cmin=20,cmax=100,t1=2,t2=2,on=0,om=2。图5显示了COPRA, BMLPA和COPRAPC算法的执行时间，由于CPM，LFM算法的运行时间较长，本文不做比较。COPRAPC算法具有合理的时间复杂度。此外，算法的时间效率和时间复杂度方面，标签传播算法具有明显的优势，本算法的时间在同类算法中也是可接受的。

图5 算法运行效率对比的实验结果 Fig.5 Experiment results of runtime efficiency

4 结论

本文提出了一种改进的重叠社区发现算法，即基于节点的PageRank值排序和节点的聚类系数标签传播算法。节点标签的传播不按随机顺序，而是按照指定节点的PageRank值的顺序传播，设定节点聚类系数阈值对标签进行更新，进而实现对网络社区结构的划分和网络重叠节点的发现。在许多人工网络和真实世界网络的实验中，基于此思想的算法都取得了相比其他同类算法更好的效果，这也说明了该思路的可行性，同时该算法具有稳定的社区发现结果。并且该算法的时间效率和复杂度也在可接受的范围内。