视频监视前景图像估计的盲源提取方法*
王 群,薛 瑞,孙振江
(1. 北京航空航天大学 电子与信息工程学院, 北京 100191; 2. 国防科技大学 教研保障中心, 湖南 长沙 410073)
运动检测是从图像序列中检测运动目标,在视频监视的目标跟踪、活动识别和行为理解中具有重要作用[1-16]。运动检测的基本原理是从视频图像的背景中提取运动目标,也称为前景图像序列。在大多数视频监视应用中,如交通或临床监视,摄像头是固定的。因此,在静态摄像机下检测图像序列中,运动物体的运动检测方法受到广泛关注,主要包括背景消减法和时间差分法[16]。由于时间差分法对于环境噪声较为敏感,仅适用于部分室内场景,因此本文重点研究背景消减法。
传统背景消减法通过评估当前场景图像与参考背景图像像素特征的差异来提取前景图像。该方法易于实现,但对光照变化非常敏感。为了适应环境(如光照)的变化,学者们提出多种改进方法来自适应地更新参考背景,主要包括两类:第一类是改进方法关注如何用合适的概率分布对背景像素进行建模[3-13];第二类是改进方法关注如何构建不包含移动对象的参考背景图像[14-16]。
在第一类改进方法中,背景中的每个像素都被建模为服从特定分布(如高斯分布[3-4]和混合高斯分布[5-9])。文献[10]提出了用非参数核密度估计来评估背景像素的概率,文献[11-12]对其进行了改进,以减小计算量。文献[13]提出了视频背景提取算法,为每个像素存储一组过去在相同位置或邻近区域获取的值,通过将该集合与当前像素值进行比较,以确定该像素是否属于背景。然而,在实际应用中,针对较快变化的背景,上述方法的背景更新过程占用了大量的计算时间。随着图像尺寸的增加,第二类改进方法受到越来越多的关注。
第二类改进方法将运动目标视为前景图像,视频监视图像视为背景图像和前景图像的叠加或线性混合,将前景对象作为当前帧和参考背景图像之间的差异进行检测[14],因此计算速度快。学者们分别提出了基于主成分分析(Principal Component Analysis, PCA)[15]、独立成分分析(Independent Component Analysis, ICA)的方法[16],在图像处理中获得了广泛应用[17-19]。然而,实际上视频的背景图像和前景图像通常是相关的。基于PCA的方法仅能提取方差最大的主成分,而主成分可能不包含前景图像信息。基于ICA的方法要求背景图像和前景图像独立,也无法进行很好的提取。因此,如何从相关的源图像中提取期望的前景图像成为一个难题。
在信号处理领域,盲源提取(Blind Source Extraction, BSE)是一种利用先验特性提取期望信号的重要手段[20-21],与PCA、ICA等盲源分离(Blind Source Separation, BSS)方法相比,BSE精度更高、鲁棒性更好。BSE包括使用高阶统计量(Higher Order Statistics, HOS)[20]和二阶统计量(Second Order Statistic, SOS)[22-26]两类方法。其中,基于线性预测器或自回归(AutoRegressive, AR)模型[22-23]SOS的BSE方法计算量小,适用于对实时性要求较高的应用。Wang等证明了当任一期望信号的AR参数已知时,如果源信号相互独立,基于均方交叉预测误差(Mean Square Cross Prediction Error, MSCPE)的BSE算法可以提取期望信号[22-23]。MSCPE能满足特定AR模型参数的要求,并能根据给定的AR参数提取任意期望信号。
基于上述研究,本文将MSCPE从独立源信号中期望信号的提取推广到相关源信号中期望信号的提取,提出一种背景消减的盲源提取方法,可以在前景图像与背景图像相关的条件下,直接从混合观测矩阵中提取前景图像,计算速度快,且可以适应不同光照变化。
本文首先给出了视频监视图像中运动检测的线性混合模型,然后给出了基于MSCPE从相关源中提取期望信号的理论证明,提出了基于盲源提取的背景消减方法,随后基于人工数据和真实数据进行了实验验证,最后提出了基于MSCPE的背景消减方法。
1 视频监视中的盲源提取模型
图1所示为监视视频中的一帧,运动检测的目的是将运动的物体(见图2)从背景(见图3)中分割。运动的物体也称前景图像,因此,感兴趣的图像(见图1)也可以看作是背景(见图3)和前景(见图2)的线性混合。

图1 源于视频的图片Fig.1 An image in a video

图2 从图1中抽取的前景图片Fig.2 Extracted foreground image from Fig.1

图3 从图1中抽取的背景图片Fig.3 Extracted background image from Fig.1
假设二维图像f∈RM×N,通过如下变换将其重构为矢量。
x(n)={x[(i-1)N+j]=f(i,j)}
i=1,2,…,M;j=1,2,…,N
n=1,2,…,M×N;x∈RMN×1
(1)
令向量sf(n)表示前景图像,向量sb(n)表示背景图像,源信号s(n)可以表示为:
s(n)=[sf(n),sb(n)]T,s∈R2×MN
(2)
感兴趣的视频监视图像x(n),可写为:
(3)
式中,x(n)表示图像序列xj(n),j=1,2,…,K;K=M×N表示一幅图像的像素数;A∈RK×2是混合矩阵。
式(3)的物理意义为:目标图像是背景和前景图像的线性混合。x(n)包含两个图像,一个是参考图像xr(n),另一个是感兴趣图像xi(n)。其线性模型可进一步写为:
(4)
运动检测的目的是通过观察量x(n)提取前景图像sf(n)。
上述问题可以看作是一个BSE模型,其目标是在模型y(n)=wTx(n)中求解向量w。然而,源信号之间通常是相关的,而非独立的。因此,本文利用相关系数(Correlation Coefficient,CC)度量提取信号se和原始信号so之间的相关性,记为:
(5)
其中,se和so具有零均值和标准方差。
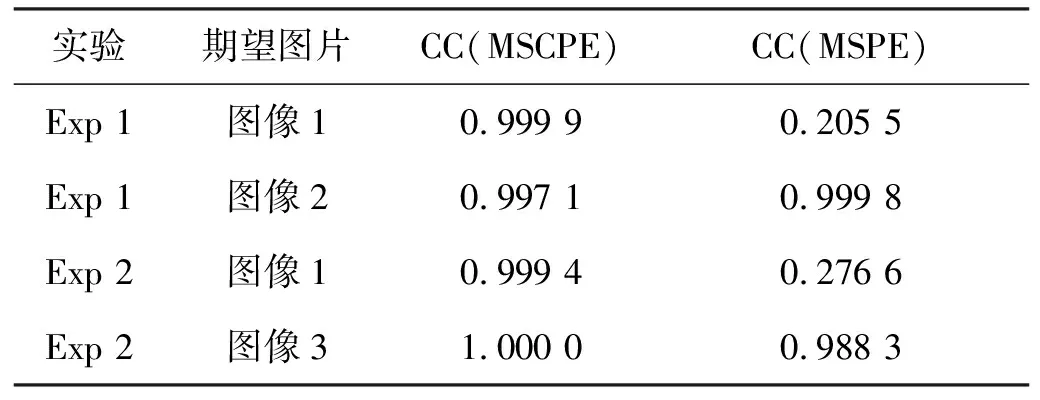
表1给出了背景图像(见图3)和前景图像(见图2)对应的相关系数,表明实际图像是相关的。

表1 背景和前景的CC值
传统的BSS信号提取方法,如PCA和ICA等,通常在操作前进行去相关,因此无法一次提取线性混合的相关信号。
2 基于MSCPE盲源提取的背景消减法
本节介绍基于MSCPE[18,20]的盲源提取基本原理,并将其用于前景图像与背景图像相关下的背景消减。
2.1 基于AR参数的盲源提取
在盲源提取问题中,N维随机信号向量x(n)形如x(n)=As(n),其中A为混合矩阵,s(n)为源信号向量。盲源提取的目的是在形如y(n)=wTx(n)的式子中求解向量w,从而估计源信号。为了使算法更加简便快捷,通常利用预白化处理将观测到的信号x变换为Hx,使得E{HxxTHT} =I,其中H为白化矩阵,E{}表示求期望。此外,预白化处理也可以帮助处理病态条件。方便起见,假设x是预白化处理的结果,并且具有与s相同的维数。
假设已知期望信号的AR参数,p表示AR模型的长度,e(n)表示瞬时预测误差(Prediction Error, PE),形如:
(6)
其中,b是期望信号的AR参数。
输出y的平均交叉预测误差(Mean Cross Prediction Error, MCPE)[22-23]可以表示为E{e(n)e(n-q)},其中q表示误差延迟。相应的e(n)为:
e(n)=y(n)-bTy(n)=wTx(n)-
[b1,b2,…,bP][wTx(n-1),wTx(n-2),…,wTx(n-p)]T
(7)
假设:
(8)
并且
(9)
MCPE可看作E{e(n)e(n-q)},有:
E{e(n)e(n-q)}
=E{wTAz(n)zT(n-q)ATw}
=wTAE{z(n)zT(n-q)}ATw
(10)
假设:
Z(q)=E{z(n)zT(n-q)}
(11)
MCPE为:
E{e(n)e(n-q)}=wTAZ(q)ZT(q)ATw
(12)
均方交叉预测误差为wTAZ(q)ZT(q)ATwT,是文献[22]中提取期望信号的代价函数。相应的代价函数的简单形式为:
Jq(w)=wTAZ(q)ZT(q)ATw, 0 s.t.wTw=1 (13) 令Σ=Z(q)ZT(q),为对角阵,其对角元素Σ(i,i) (i=1,2,…,M)等于源信号s(i), (i=1,2,…,M)MCPE的平方。如果源信号的AR模型参数不同,则上述代价函数最小为零。因此,可以通过最小化代价函数来提取所需的信号Jq(w)。 由于在约束wTw=1下最小化代价函数Jq(w)等价于求实对称矩阵AZ(q)ZT(q)AT最小特征值的特征向量,w等价于Z(q)最小奇异值的奇异向量。因此有以下算法[22]: (14) 其中,MINEVD{M}是计算实对称矩阵M的归一化特征向量对应的最小特征值的算子,MINSVD{M}是计算矩阵M的归一化奇异值向量对应的最小奇异值的算子。 当存在不同结构时[25-26],可以通过最小正规化MSPEE{e2(n)}/E{y2(n)}来提取源信号。由于x是经过白化处理的,因此去混合标量E{y2(n)}的输出功率是一致的。代价函数可以设为MSPE,即E{e2(n)},其表达式如下: E{e2(n)}=wTARpATw (15) 并且 (16) 从BSS的角度来看,本质是在被估计的信号y(n)=WTx(n)中求解矩阵W。式(14)对W的求解可以看作 W=SVD{AZ(q)AT} (17) 或 W=EVD{AZ(q)ZT(q)AT} (18) 其中,EVD{M}是计算实对称矩阵M的所有归一化特征向量算子。SVD{M}是计算实对称矩阵M的所有归一化奇异向量算子。 文献[22]和文献[23]证明,如果任何期望信号的AR参数已知,MSCPE将会避免排列问题[22],并可以提取期望信号[23]。本文将MSCPE推广到以相关源信号为基础,提取期望信号。 定理1 在无噪声BSE问题中,观测量x(n)形如x(n)=As(n),其中A为未知混合矩阵,s(n)为源信号向量,假设: 1)源信号之间是相关的; 2)每个源信号满足: E{si(n)si(n-τ)}=0,τ>0 3)某期望信号的AR参数已知; 4)观测量x与源信号具有相同的维度。 那么,当期望信号的MSCPE值小于任意一个源信号时,式(14)的算法可以有效提取出信号。 (19) 经施密特变换[13],有 (20) 由假设2可知: (21) 又由于x(n)=As(n)=ABs′(n),为便于后续推导,假设A=AB和s(n)=s′(n)。 当式(18)成立时,Z(q)则为对角阵,Z(q)ZT(q)为非负对角阵,当x经过白化处理后,即E{xxT}=I,A将成为正交矩阵。表示为Λ=Z(q)ZT(q)。AZ(q)ZT(q)AT的奇异值分解可表示为:[A,Λ,AT]=SVD(AZ(q)ZT(q)AT) 对于给定期望源信号sk的AR模型参数b,其中k为期望数,各源信号的MCPE可表示为[18]E{ej(n)ej(n-q)} (j=1,2,…,N)。其中ej(n)表示残留误差。由于源信号具有不同的AR参数,有以下特性: (22) 其中: (23) 其中,p是AR参数的长度,因此,Λ的第k个对角元素为最小对角元素且为0。 在约束条件wTw=1下,最小化代价函数Jq(w)等价于求实对称矩阵AZ(q)ZT(q)A的最小特征值对应的特征向量。 因此,如果期望信号的MSCPE值小于任意源信号,则式(14)的算法可以提取期望信号。 □ 以上定理表明,即使源信号之间互相关,MSCPE盲源提取方法可以通过最小化MSCPE值提取出所需的期望信号。此外,MCPE盲源提取方法可以通过最小化MCPE值提取期望信号。因此,从相关源信号中提取期望信号的关键是,找到合适的参数使相应的MSCPE值最小,其中MCPE是MSCPE的特殊情况。 综上,当期望信号的AR参数已知时,MSCPE盲源提取方法可以从线性混合源中提取期望信号。 在采用了MSCPE的BSE算法中,由序列中的参考背景图像和当前场景图像组成数据矩阵,是背景图像和前景图像的混合。 基于BSE的背景消减方法包括粗提取和精提取两个阶段。在粗提取阶段,利用MSCPE算法将数据矩阵与参考背景图像的AR参数进行去混合,得到两幅估计图像:其中一幅是背景图像的精细估计,另一幅是前景图像的粗略估计。在精细提取阶段,利用MSCPE算法将数据矩阵与估计的前景图像的AR参数进行去混合,估计出精细前景图像。 在粗提取阶段,由于提取的两幅图像互不相关,利用参考背景图像的AR,背景图像的估计相对较好,前景图像的估计相对粗糙。 如果背景图像和前景图像是独立的,得到的前景图像在粗糙状态下的估计就是解,这两个阶段合并为一个阶段。而背景图像和前景图像通常是相关的,此时两个阶段是必要的。 基于ICA (BSS)的方案通常包含两个阶段:训练阶段和检测阶段。与基于ICA的方法相比,基于MSCPE的方法有如下两个优势: 1)基于MSCPE的方法使用的二阶统计量相对于基于ICA方法使用的高阶统计量运算开销小; 2)MSCPE无须训练阶段,更加智能。 在本节中,使用MSCPE提取视频监视中需要的前景图像,以验证该方法的可行性。 本实验利用实际数据人工混合来评估MSCPE的性能。实验选择了3组图片,如图1~3所示。图1为视频图片,另外两张分别为前景图片和背景图片。然后进行两组实验,分别记为Exp 1和Exp 2。 Exp 1涉及Image 1和Image 2,Exp 2涉及Image 1和Image 3。 在每个实验中,假设期望信号的AR模型参数已知,使用MSCPE提取期望信号。另外,背景图像和前景图像将分别作为所需的信号。 实验步骤如下: Step1: 选择背景图像和前景图像作为源信号s(n); Step2: 生成混合数据x(n)=As(n),其中A∈R2×2表示混合矩阵,由MATLAB随机生成; Step3: 为提取期望信号选择特定参数p和q,(本文p=60,q=1); Step4: 利用MSCPE提取期望信号,其中期望信号的AR模型参数由MATLAB中函数“aryule”计算得到; Step5: 对提取的信号进行标准归一化,并计算对比相应的CC。 实验同时使用MSCPE和MSPE提取期望信号。实验结果如表2所示,其中CC(MSCPE)是由MSCPE求出的提取信号和期望信号计算而得。CC(MSPE)是用MSPE计算的CC。两种CC值都是通过100次仿真实验求平均得到。 表2 Exp1和Exp2的实验结果 由表2可知,MSCPE提取的图像与期望图像之间的CC值均大于99%,而MSPE在Exp 1中图像2和Exp 2中图像3的提取效果较好,在两个实验中图像1的提取效果较差。这是因为MSPE来自ICA,能够很好地提取独立的源信号,而表1中计算的CCs表明,背景和前景图像不是独立的,而是相互关联的。因此,ICA很难从相关源中提取独立的源信号。 备注1 (参数选择): 在MSCPE中涉及两个参数p和q。尽管式(16)表明,在选择不同的q时,对于期望信号MCPE为零,而MCPE的值不为零,甚至在实际中,对于固定的q,其值可能并非最小值。这种现象有两方面的原因:一是AR参数计算中累积误差的影响;二是源信号是相关的,这使得期望信号的AR参数与相关信号的AR参数相似。在这种情况下,p和q的选择主要依赖于仿真中的试错。 备注2 (q的选择): 注意到第3.1节中对q选择,不同的材料,A是不同的,而这部分采用q=1。理论上来说,q>1不会影响对源信号的估计。但在数值计算中,q取值越大会要求BSE模型的维数较大,进而会增加SVD计算的累积误差。因此,需要在q和累积误差之间进行权衡,本实验选择q=1。 通过第2节的理论分析以及第3.1节的实验结果表明:MSCPE可以从相关源中提取期望信号。本节进而利用MSCPE在BSE框架下,从数据矩阵中提取前景信息。该数据矩阵是由背景图片和当前场景图片组成的序列。 该方法涉及粗提取和细提取两个阶段。 Step1: 粗提取。采用MSCPE算法,利用式(17)或式(18)对参考背景图像的AR参数进行去混合。然后用矩阵AZ(q)ZT(q)A最小特征值对应的归一化特征向量将信号分离为背景图像的精细估计,另一分离信号为前景图像的粗估计。 Step2: 细提取。根据第一阶段对前景图像粗估计的AR参数,采用MSCPE算法,利用式(14)将与第一阶段相同的矩阵进行分层。 在上述两阶段的基础上,分别对单参考背景和多参考背景进行测试。并与图像差分法和粗糙阶段的结果进行对比。 单参考背景即参考背景平稳。在该示例中,仅改变了照明。测试房间有两组荧光灯。灰色的视频图像是10帧/s。在第62帧之前有一组灯被关闭,之后两组灯都被打开。 图4 (a)给出了一个视频序列中的离散场景图像,其帧数分别为10、85和150。选取帧数为10的图像作为参考图像,其光照强度与另外两幅检测图像不同。图4(b)、图4(c)和图4(d)分别给出了利用两阶段方法、图像差分方法以及粗提取(第一阶段的结果)方法提取到的前景图片。由于帧数为10的图像被作为参数,因此对其提取的前景图像的所有像素为0,即图4中第1行后3幅图像。 图4(b)表明,本文提出的两阶段提取方法可以很好地提取期望前景图像。图4(c)表明,在参考图像和场景图像光照不同的情况下,传统的图像差分方法效果不佳。图4(d)表明,粗估计使得前景图片在背景中相当突出,并且包含了部分背景信息。这是由于背景图像与前景图像相关性的影响。 对图4中图像进行二值化,结果如图5所示。图5(b)~(d)分别给出了所提出的两阶段法、图像差分法以及粗糙阶段法的二值化结果。 由图5可知,本文所提方法可以在室内光照条件下提取出理想的前景图像。当光线变化时,场景中物体的反射率会发生变化,进而会引起图像大小的改变。值得注意的是,信号大小的变化对信号的AR模型参数影响较小。进而说明该方法对光照变化具有较强的鲁棒性。 多参考背景是非平稳(动态)的。例如,房间里窗帘的形状经常受到风或行人的影响。第二个室内测试样本是一个人沿着房间的窗帘走。测试房里有两组荧光灯。灰色的视频图像拍摄于10帧/s。在第108帧之前有一组灯被关闭,之后两组灯都被打开。 图6(a)分别给出了第5帧、65帧、145帧的离散场景图像。帧数为5的图像被作为参考图像,因此对其提取的前景图像的所有像素为0,即图6中第1行的后3幅图像。图6(b)、图6(c)和图6(d)分别给出了利用两阶段方法、图像差分方法以及粗提取(第一阶段的结果)方法提取到的前景图片。图6(b)和图6(d)表明,本文提出的两阶段提取方法和粗估计方法可以很好地提取期望前景图像。图6(c)表明,传统的图像差分方法在多参考背景下效果较差。 对图6中图像进行二值化,结果如图7所示。图7(b)~(d)分别给出了所提出的两阶段法、图像差分法以及粗糙阶段法的二值化结果。 由此可知,在多参考背景下,粗糙估计方法和所提出的两阶段估计方法都是可行的。这是由于多重参考背景在式(3)的无噪声模型中引入了噪声。 x(n)=As(n)+V(n) (24) 其中,V(n)表示添加的噪声,物理意义为当前背景和参考背景之间的差异。通常有两种处理含噪BSE的方法:一是忽略噪声;二是采用噪声消除技术。第二种方法的大部分算法都是基于加性高斯噪声。由于加性噪声难以建模,因此采用无噪声BSE算法提取期望信号更为适合。 引入的噪声将不可避免地影响前景图像的AR参数估计,进而降低精细估计的效果。然而,本文所提出的方法仍然可以很好地提取期望前景图像。 由于MSCEP算法可以从相关源中提取所需的信号,因此该算法也可以用于其他背景消减框架,如基本模型方法和特征背景方法。 对于基本的背景消减法模型,主要的方法是检测前景对象作为当前帧,与场景静态背景图像之间的差异为: |Framei-Backgroundi|>Threshold (25) 解决上述问题的关键是如何自动获取场景的静态背景图像。一是选择背景作为前n帧的平均值或中值[14],该方法运算速度快,但对内存的开销较大,内存需求是框架大小的n倍。二是采用运行平均值: Backgroundi=αFi+(1-α)Backgroundi-1 (26) 其中:Fi表示当前场景图片;α表示学习速率,一般取0.05。该方法对内存需求不大,但是如果当前场景图片Fi包含了前景信息,则性能会严重下降。而MSCEP算法可以采用第一阶段粗略提取背景图像,去除或至少减少前景图像的影响,如图8所示。 图8(a)和图8(b)分别显示背景图像和前景图像的场景图像,两幅图片被重新排列为数据矩阵X。图8(c)为在数据矩阵中利用第一阶段方法对前景图片进行粗提取。由图8(c)可知,在保留了背景图片的前提下,前景图片得到了弱化。为了进一步验证性能,对图8(b)和图8(c)进行零均值标准归一化,并在图8(c)中减去图8(b)得到图8(d),其二值化结果如图8(e)所示。实验结果表明,当前场景图片Fi包含前景图片时,MSCPE方法仍然能够取得较好的结果。 对于特征背景模型[15],主要是利用主成分分析对n帧序列的背景特征进行计算。其主要步骤如下: Step1: 对n帧进行重排列,得到矩阵X∈Rn×l,其中l是场景图像的像素个数; Step2: 计算协方差矩阵C=XTX,C∈Rl×l; Step3: 利用协方差矩阵C,计算由特征值组成的对角阵E以及特征向量所组成的矩阵Φ; Step4: 只保留前m个较大特征值对应的特征向量,将其记为G,其中,G∈Rm×l; Step5: 当前场景图片I(1×l)可用时,将其在G中进行投影,并重构为I′=IGTG; Step6: 计算I与I′的差值,其差值即为前景图片。 根据特征值的思路,基于MSCPE的特征背景方法的步骤如下: Step1: 对n帧进行重排列,得到矩阵X∈Rn×l; Step2: 利用式(7)~(11)对协方差矩阵进行计算,C=AZ(q)AT,其中,C∈Rn×n; Step3: 根据式(17)或式(18),利用协方差矩阵C,计算由特征值组成的对角阵E以及特征向量所组成的矩阵Φ; Step4: 只保留后m个较小特征值对应的特征向量,将其记为W(n×m); Step5: 记G为m行特征向量子空间,并由G=WTX计算得到,其中,G∈Rm×l,当前场景图片I(1×l)可用时,将其在G中进行投影,并重构为I′=IGTG; Step6: 计算I与I′的差值,其差值即为前景图片。 图9给出了使用修改后特征背景的多个参考背景实验结果,其中m=4,n=10。图9(a)~(d)表示最后m个特征向量构成一个空间,图9(e)为视频中第145帧图片,对其使用MSCPE方法提取的背景图像如图9(f)所示,对图9(e)和图9(f)做差得到前景图像如图9(g)所示,其二值化结果如图9(h)所示。由该图可知,基于MSCPE的特征背景方法可以很好地提取前景图像。仿真实验进一步表明,基于MSCPE的特征背景方法和原始特征背景方法一样有效。由于篇幅所限,仿真结果未一一列出。 值得注意的是,当m=1时,基于MSCEP的特征背景方法将退化为基于MSCEP的基本模型方法。因此,基于MSCEP的基本模型方法实际上是基于MSCEP特征背景方法的一种特例。图9(c)和图9(f)表明,基于MSCEP的特征背景方法提取的背景图片仍然包含了非前景图片,而基于MSCEP的基本模型方法提取的背景图片仍然会受到前景图片的影响。对比表明,扩展子空间对背景图像的提取是有效的。 与此同时,基于MSCEP特征背景方法的性能大部分时候较基于MSCEP的基本模型方法好。当n帧矩阵X包含前景图像时,如果m>1,特征背景方法就无法工作;当m=1时,基于MSCEP的特征背景方法将退化为基于MSCEP的基本模型方法,可以正常工作,然而此时特征背景方法效果不佳,如图10所示。图10分别给出了第5帧、145帧、165帧构成矩阵X,图10(d)为利用PCA得到的重构图片。由图可见,重构图片受到了前景图片干扰。相比而言,MSCPE能够较好地提取背景图像。然后通过相应的背景消减法和二值化结果,验证了基于MSCPE的方法优于PCA或特征背景法。 综上,对于第二类背景消减的改进,有三种方法:基本模型、基于PCA的模型和基于ICA的模型。MSCPE算法可以结合这三种方法,提高算法的鲁棒性,进而用于人机交互[27]、目标跟踪[28]和人脸识别[29]问题。 理论上来说,如果对源信号加入适当的约束(非负约束、瞬时结构等[21]),相关源的准确提取仍然是一个具有很大挑战的问题。除了BSE外,其他的线性变换,如邻域线性嵌入[30]和局部线性嵌入[31],可能也会被嵌入背景提取中,这将是下一步研究的重点。 在视频监视中,一个(帧)场景图像可以被建模为前景和背景视觉内容的线性混合,而实际上图像的背景和前景往往是相互关联的。为了解决从与其他源信号相关的观测数据中提取期望信号的问题,本文将MSCPE推广到视频监视的前景图像提取中。通过对实际视频图像的处理,验证了该框架下算法的效果和效能。 在单参考背景下,前景提取可以看作是一个无噪声BSE问题。传统的图像差分方法对光照变化很敏感,这是由于图像的大小变化造成的。由于信号的AR参数对信号大小的变化不敏感,因此该方法的对光照变化具有鲁棒性。在多参考背景的情况下,后处理模型可以看作是一个有噪声BSE问题。由于加性噪声难以建模,因此采用无噪声MSCPE算法提取期望信号,在提取期望前景图像时仍表现良好。 MSCPE还可以用于其他背景消减方案,如基本模型和特征背景模型,从而构成了一个自动化和鲁棒性性能更好的算法框架,可以有效去除或减小前景图像的影响。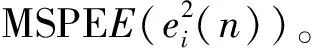
2.2 相关源的MSCPE盲源提取
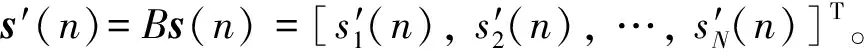
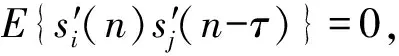
2.3 基于盲源提取的背景消减方法
3 仿真实验
3.1 真实图像的人工混合
3.2 单参考背景的真实视频图像

3.3 多参考背景的真实视频图像


4 讨论
4.1 基于MSCPE的基本模型

4.2 基于MSCPE的特征背景模型



5 结论

