风场中平流层飞艇轨迹跟踪的滑模控制方法*

杨希祥，张家实

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073;2. 湖北航天技术研究院 总体设计所， 湖北 武汉 430034)

平流层飞艇利用临近空间下层稳定的环境风场，可以实现月年量级的长期驻空，被形象地称为“平流层卫星”，应用前景广阔，是军事强国和互联网巨头竞相发展的战略前沿领域[1-2]。

长期区域驻留是平流层飞艇最显著的特征和优势，有效实现轨迹跟踪控制是平流层飞艇实现长期区域驻留的重要保障。轨迹跟踪控制是指操纵平流层飞艇按照预定的轨迹飞行。平流层飞艇的总体布局、飞行机理以及工作模式明显不同于飞机、导弹等飞行器，它是一个复杂的被控对象，轨迹跟踪控制面临控制布局受限、风场扰动影响显著、长时延等诸多难题，亟待深入探索研究。

国内外学者针对平流层飞艇及低空飞艇航迹控制问题的已有研究方法大致可分为三类：借助优化理论和方法来解决航迹优化控制问题、基于线性化模型的航迹控制方法、非线性航迹跟踪控制方法。文献[3]是目前可查的最早关于平流层飞艇航迹规划与控制的文献，采用线性系统中的最优控制理论，设计了平流层飞艇最优上升航迹控制指令；Paiva以AURORA飞艇为研究对象，分纵向高度控制和侧向航向控制两个通道，采用PI控制方法设计了航迹控制器[4]；Avenant采用模糊控制方法，实现了对飞艇航迹的有效控制，并在系统参数时变和外界干扰条件下验证了控制系统的鲁棒性[5]；文献[6]和文献[7]研究了风场中低空飞艇航迹控制问题，采用线性二次型方法设计了线性航迹控制器，其方法主要适用于二维航迹跟踪问题，对于三维航迹跟踪问题误差较大。文献[8]首先研究了平流层飞艇最优轨迹规划，然后采用反步法设计了全局稳定的非线性航迹跟踪控制器，文献[9]也采用反步法设计了平流层飞艇非线性航迹跟踪控制器。

本文采用对外部扰动和参数不确定性具有较好鲁棒性的滑模控制方法，实现风场中平流层飞艇驻空轨迹跟踪，为平流层飞艇动力学与飞行控制研究提供理论参考。

1 平流层飞艇动力学模型

将平流层飞艇视为轴对称外形，即体积中心和浮力中心重合，在体坐标系(ob-xbybzb)中建立动力学方程[10-12]，即

=B+G+T+R+Fw

(1)

M=mE3×3+Ma

(2)

式中：m为飞艇质量；Ma为附加质量矩阵；E3×3为单位矩阵；Vo=[u,v,w]为速度；ω=[p,q,r]为艇体绕浮心的角速度；p,q,r分别为滚转、俯仰和偏航三个方向的角速度；ω×为ω的叉乘矩阵；rG=[xG,yG,zG]为浮心到质心的距离；B，G，T，R，Fw分别为浮力、重力、螺旋桨推力、气动力和风场产生的环境力。

在体坐标系中建立飞艇绕浮心动力学方程， 即

=NR+NC+Ng

(3)

I=Io+Ia

(4)

式中：Io为转动惯量矩阵；Ia为附加惯量；NR，NC，Ng分别为气动力矩、矢量控制力矩、重力矩。Io定义为

式中：Ix，Iy，Iz分别为绕体坐标系三轴的转动惯量；Ixy，Ixz，Iyz为惯量积。

为研究问题方便，将式(1)和式(3)中的动力学方程解耦为横侧向运动和纵向运动，并采用小扰动线性化方法，将横侧向动力学方程线性化，得到，

(5)

式中，

2 平流层飞艇轨迹跟踪滑模控制器

2.1 设计思路

滑模控制是一种鲁棒性较强的控制方法，其基本原理是，首先定义一个滑模面；然后使系统轨迹向滑模面靠近，当到达滑模面附近时，控制其在滑模面附近滑动并最终到达滑模面；此外，控制其轨迹稳定在滑模面内，并沿滑模面运动直至系统到达原点(期望状态)。

滑模控制器设计步骤包括两部分[11-12]：

1)滑模面参数设计：设计切换函数s(x)，切换函数直接关系到系统滑动模态稳定性与动态性能。切换面需保证系统滑动运动渐进稳定，且动态品质好。

2)滑模控制律设计：设计控制量u+(x)和u-(x)，使系统满足到达条件，即使系统状态可以从状态空间初始点运动到滑模面，并稳定保持在滑模面上做滑动模态运动。

2.2 轨迹跟踪滑模控制器

选取切换函数，即

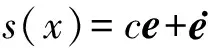
(6)

对于平流层飞艇驻空期间水平轨迹跟踪控制，系统轨迹采用地面惯性系中的位置和飞艇偏航角表示，误差定义为当前时刻实际轨迹与指令轨迹之差[12]，即

(7)

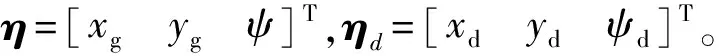
为消除滑模控制的抖振，选择指数形式的趋近律，

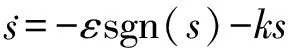
(8)

将式(6)和式(8)联立，得

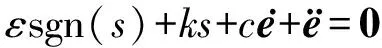
(9)

将误差二阶导数代入式(8)，得

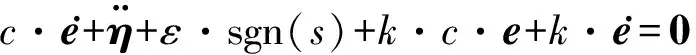
(10)

(11)

对式(11)进行微分运算，得

(12)

联立式(5)、式(11)、式(12)，得到实际轨迹二阶导数、一阶导数与控制变量的关系，则

(13)

结合式(10)，得到滑模控制律U，

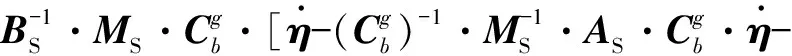
(14)

平流层飞艇轨迹跟踪的滑模控制器控制回路如图1所示。

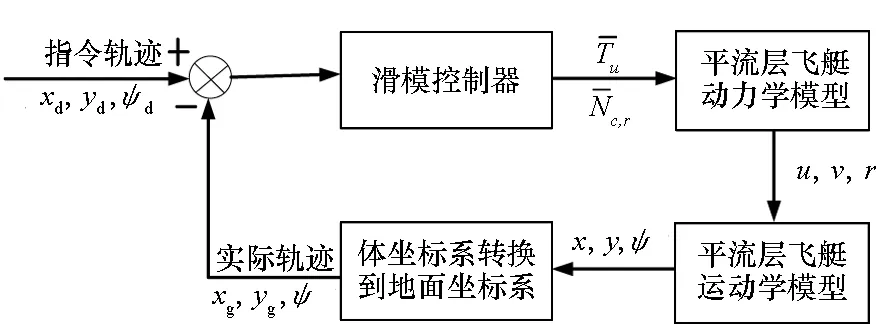
图1 平流层飞艇轨迹跟踪滑模控制器Fig.1 Sliding mode controller for trajectory tracking of stratospheric airship

3 仿真结果及分析

3.1 仿真条件

以美国HALE-D飞艇为研究对象，以直线与圆构成的组合轨迹跟踪为例，对所提基于滑模的轨迹控制方法进行仿真验证。HALE-D飞艇主要参数如表1所示，风场分解为轴向风速和侧向风速，仿真过程在10～20 m/s范围内随机取值。

表1 HALE-D飞艇主要参数

平流层飞艇先做直线轨迹跟踪运动，然后做圆轨迹跟踪运动，指令轨迹初始状态为，

[xd(0),yd(0),ψd(0),ud(0),vd(0),rd(0)]T

=[0 m,0 m,0.2 rad,25 m/s,0 m/s,0 rad/s]

平流层飞艇实际轨迹初始状态为

[x(0),y(0),ψ(0),u(0),v(0),r(0)]T

=[0 m,0 m,π/2 rad,25 m/s,0 m/s,0.1 rad/s]

直线轨迹跟踪阶段，滑模控制器参数取值为

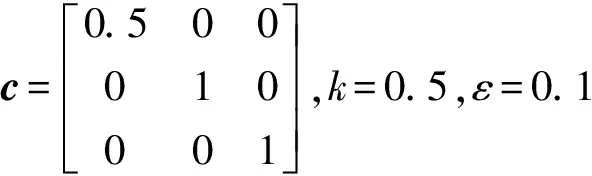
圆轨迹跟踪阶段，滑模控制器参数取值为

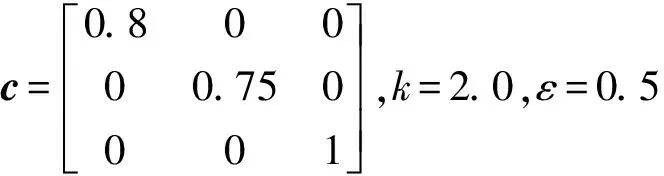
3.2 结果分析

平流层飞艇轨迹跟踪结果如图2～3所示。

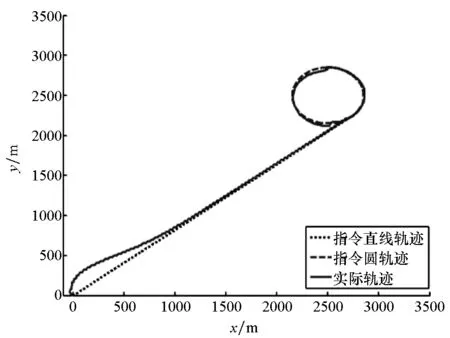
图2 轨迹跟踪结果Fig.2 Simulation results of trajectory tracking

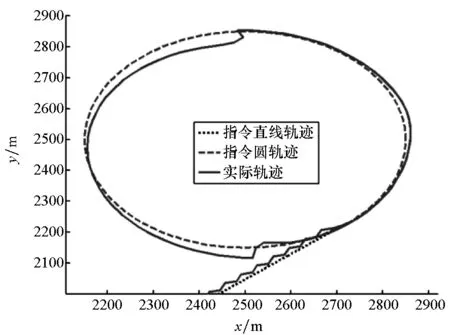
图3 圆轨迹跟踪结果局部放大Fig.3 Local enlarged drawing of simulation results

由图2和图3可以看出，在平流层飞艇轨迹跟踪的初始阶段，实际轨迹与指令轨迹偏差较大，这是因为滑模控制方法需先控制轨迹到达滑模面，在进入滑模面之前存在一段趋近运动；当实际轨迹抵达滑模面之后，开始进行滑动模态运动，通过滑模控制器校正，各状态量迅速收敛并达到稳定，实际轨迹与指令轨迹偏差较小且较为稳定。

轨迹跟踪过程侧向速度和偏航角变化如图4～5所示。

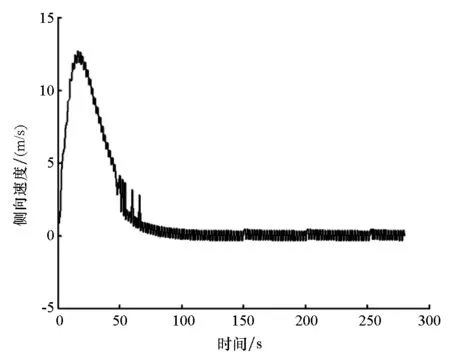
图4 侧向速度变化曲线Fig.4 Changing curve of lateral velocity

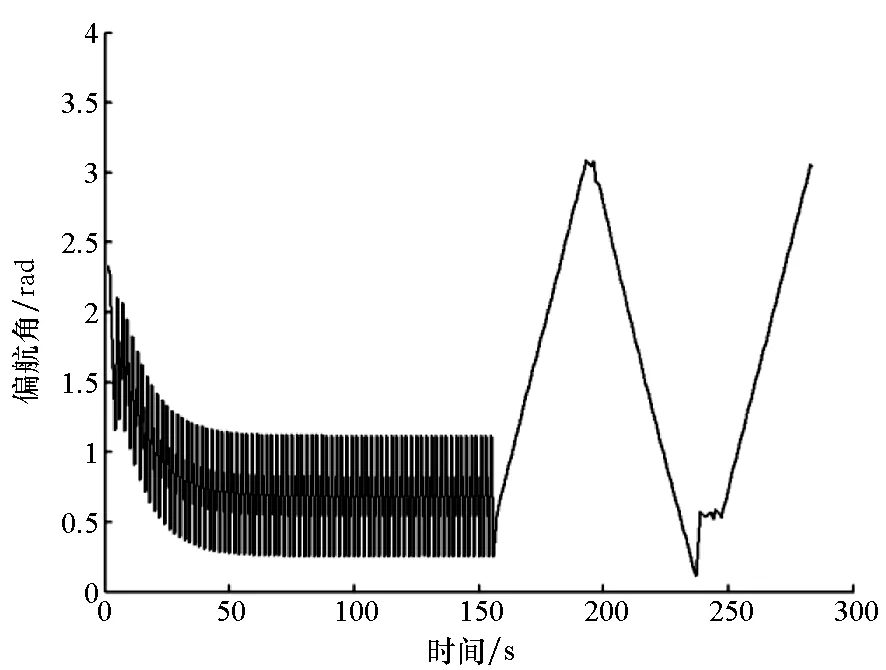
图5 偏航角变化曲线Fig.5 Changing curve of yaw angle

由图4和图5可以看出，由于随机风场干扰和滑模控制方法本身存在的抖振问题，使得状态量在达到稳定状态后存在小范围波动，这种波动会导致控制力和控制力据处于小范围波动状态。

总体来说，在风场干扰条件下，平流层飞艇从偏离指令轨迹的初始状态开始运动，在较短时间内到达滑模面，进行滑动模态运动，各状态量之间的偏差均渐近收敛，响应速度较快、滑模控制器具有较强的鲁棒性，可在一定范围的外界干扰条件下实现直线和圆轨迹的有效跟踪控制。不足之处在于，对于平流层飞艇这样大惯量、长时延的控制对象，在前0～150 s，偏航角波动频率较高，会给实际操作形成挑战，后续将围绕这一问题开展深化改进研究。

4 结论

本文研究了风场中平流层飞艇轨迹跟踪的滑模控制方法，主要研究工作和结论如下：

1)建立了平流层飞艇驻空阶段动力学模型，在定高飞行的前提下，采用小扰动方法对横侧向动力学方程进行了线性化。

2)基于滑模控制对外部扰动不敏感的特性，提出了平流层飞艇轨迹跟踪的滑模控制方法，设计了横侧向轨迹跟踪的滑模控制器。

3)分别以直线轨迹跟踪和圆轨迹跟踪控制为例，对所提的轨迹控制方法进行仿真验证。仿真结果表明，所设计的滑模控制器鲁棒性好，在一定范围的风场扰动条件下，可以实现对指令轨迹的有效跟踪控制，响应特性好。