焊接金属波纹管密封端面流固耦合参数分析①

，，， ，， ，

(1．四川大学 制造科学与工程学院，四川 成都 610065；2．四川日机密封件股份有限公司，四川 成都 610045；3．独山子石化公司 聚烯烃一联合车间，新疆 独山子 833699)；

在机械密封中，与补偿环连接元件为焊接金属波纹管的密封形式称为焊接金属波纹管机械密封[1]。焊接金属波纹管机械密封靠弹性补偿元件、流体压力及辅助密封的配合使密封端面相互贴合并相对转动。由于动、静环的表面加工精度很高，在密封介质的作用下，可以产生流体动压效应并在端面维持一层极薄的液膜，使密封端面处于混合摩擦状态，以达到密封的目的。

常见的内装型机械密封结构见图1[2]。机械密封安装在旋转轴轴套上，焊接金属波纹组件(2个焊接金属波纹管座)与补偿环组件(静环座、静环)连接在一起，且它们与轴套之间有微小间隙。当密封端面磨损后，依靠弹力自动补偿密封端面磨损，非补偿环组件(动环、动环座)、紧固螺钉与旋转轴相连并随之转动[3]。弹性补偿单元(焊接金属波纹管)起预压缩、磨损补差及减小振动的作用，具体包括为密封端面提供一定的弹性压力使其形成合理比压、传递一定的旋转力矩以及保持稳定的弹簧力来抵消非主要密封传动件的摩擦力。

1.旋转轴 2.紧固螺钉 3.动环座 4.动环5.静环 6.静环座 7.焊接金属波纹管 8.焊接金属波纹管座 9.辅助密封圈 10.密封腔体

西安石油大学高昊[4]采用GAMBIT软件建立了液膜三维模型，并应用FLUENT软件对端面液膜进行了参数分析。大连理工大学王宁[5]采用有限差分法对滑动轴承压力分布进行了数值计算。从国内外研究现状看，鲜见对密封端面的流固耦合分析。文中介绍了端面流固耦合分析所需的密封理论基础和方法，采用FLUENT、ANSYS Workbench有限元软件对焊接金属波纹管机械密封端面液膜进行压力场及端面耦合分析，将转速、介质压力设为输入参数，压力场分布、端面速度、泄漏量设为输出参数进行参数化分析求解，得到了密封端面压力分布及泄漏量与介质压力、转速的关系。

1 机械密封端面密封理论模型

1.1 端面受力

接触式机械密封在稳定工作时端面通常处于混合摩擦状态，其受力情况见图2。

图2 接触式机械密封稳定工作时端面受力示图

机械密封端面工作时主要受到液膜压力Fm、接触力Fc形成的开启力以及波纹管弹力F、介质压力Fp形成的闭合力，两者在密封端面形成力平衡，维持端面液膜及密封稳定，如式(1)。

Fc=F+Fp=Fm

(1)

1.2 液膜压力计算

在密封端面上，流体静压ps和流体动压pd决定了液膜压力Fm的大小。沿半径r取微元dr，其单位面积压力为pr，则平面上开启力为Fs：

(2)

(3)

(4)

式中，p为介质压力，MPa。

令h0为液膜出口厚度，h为端面间隙，η为流体动力黏度，v为流体线速度，则流体动压pd为：

(5)

以平行平面端面密封为研究对象，有h=h0、pd=0 MPa，Fm由下式计算：

Fm=Fs=π(r2-r1)(2r2+r1)p/3

(6)

1.3 端面接触压力计算

端面接触压力是指单位面积上所承受的接触力，该参数对端面密封性能有极大的影响[6]。要计算密封端面接触压力，需明确密封端面接触面积，在机械密封中称为名义接触面积Af：

Af=π(r22-r12)

(7)

两密封环在粗糙度影响下的实际接触面积为Ar，Ar为Af的极小部分。在实际计算中可以用bm来表示两端面的接触比。

(8)

式中，z为轴向坐标值；δ为密封端面综合粗糙度。

则端面接触压力pc可表达为[7]：

pc=bmσc

(9)

式中，σc为材料的压缩强度，MPa。

1.4 端面力变形计算

机械密封环在工作中主要受到摩擦力，密封面上的相互接触作用力、反作用力以及液膜反力。摩擦力只能使密封面产生一个相对于中心轴线的旋转变形，对密封面工作的影响可以忽略，因此进行端面力变形分析时只考虑密封面上的接触作用力。密封面的力变形非常复杂，且环本身存在伸缩和弯曲，各点应力状态多维且未知，故利用计算机完成计算。

文中采用基于圆环理论的变形方法计算密封环端面力变形，并提出以下假设：①不考虑圆环的伸缩和弯曲，只考虑圆环截面的变形。②密封圆环中任一点的应力维度是一维的。

旋转力矩引起变形的转角为：

(10)

其中

M=pSRm

(11)

式中，M为由接触作用力产生的作用于密封环上的力矩，N·mm；Rm为密封面的平均半径，R2为密封面外半径，R1为密封面内半径，L为密封环轴向长度，m；E为密封环所用材料的弹性模量，GPa；S为接触面面积，mm2。

旋转力矩引起的变形为：

δA=φAbCF

(12)

式中，b为密封面的径向宽度，mm；CF为形状系数。

径向力引起的变形为：

δR=φRbCF

(13)

转角φR计算公式为：

(14)

其中

q4=3|v2-1|/(v2b2Rm2)

(15)

式(14)～式(15)中，p1为面均布载荷，MPa；υ为泊松比。

密封环变形量δ为：

δ=δA+δR

(16)

取密封环材料为碳化硅和YG6钨钢，其弹性模量分别为14 GPa和192 GPa，泊松比分别为0.15和0.21。将数据带入以上各式，计算得到|δ1|=0.009 9 μm、|δ2|=0.03 μm。

从计算公式可以看出，端面力变形与材料的弹性模量E成反比，与作用力矩M成正比，故应尽量选用弹性模量大的材料作为密封环材料。

需要指出，采用圆环理论得到的结果往往与实验结果差距很大，在实际情况中一般不会采用此经验算法进行计算，这种方法只能用做临时的简单分析，其精确计算结果需运用有限元法计算[8-9]。

2 机械密封端面液膜压力场有限元建模及边界设置

2.1 模型建立

目前，最理想的接触式机械密封端面接触模型是平面平行端面，其液膜分布模型可以简化为圆环(图3)[4]。

图3 平面平行端面液膜分布简化图

根据选定的模型在FLUENT中对液膜进行分析，由于FLUENT没有前处理功能，故在DM Geometry中建模，利用ICEM软件划分液膜流体网格并设定边界条件，再调入FLUENT计算。

根据密封端面结构参数在DM Geometry中建立流体液膜三维模型。由于液膜是圆环状呈轴对称分布，存在周期性，故取液膜的1/12为1个周期进行网格划分与分析，可以节省大量的计算时间。实际工作中液膜厚度仅为1.5～2 μm，而端面半径为43.5～47.5 mm，相差4个量级。为了便于建模和观察，避免修补几何时可能出现的边界相交，将膜厚放大1 000倍。建立的端面液膜有限元模型见图4，其中上端面为动环端面，下端面为静环端面，外径弧面为介质入口，内径弧面为介质出口。

图4 端面液膜有限元模型

对于大尺寸比例(4个量级)的模型，为了保证网格质量，采用ICEM软件进行网格划分，利用ICEM中Ogrid block O型网格切割划分2D平面网格，先以液膜端面为源面生成结构网格，而后拓扑出体网格，得到六面体结构网格，见图5。

将网格导入FLUENT，利用软件自带网格检查模块进行网格检查，若不符合要求需重新划分网格。由于几何建模时将轴向网格放大了1 000倍，因此在FLUENT中需将轴向网格缩小到原来的千分之一，并保证流体网格与结构网格原点重合。

图5 端面液膜网格划分

2.2 边界条件及求解设置

2.2.1边界条件确定

采用FLUENT求解流体模型，边界条件的设置对计算时长和结果精度的影响很大[10]，设置边界条件的第一要求是符合实际要求、符合数学模型。

根据FLUENT提供的边界条件，结合本次分析的具体条件，出、入口压力已知，因此在端面外径设置压力进口条件，在端面内径设置压力出口条件。为了节省计算时间，建模采用了周期模型，故在网格两端面设置周期性边界。因动环处于旋转状态，需将上端面设置为旋转壁面条件，下端面设置为静止壁面条件。

对于旋转问题，FLUENT提供了旋转参考坐标系和旋转网格两种解决方法。对于带简单旋转元件的流体分析，采用旋转参考坐标系方法可以得到较为精确的计算结果，本文采用该方法。

2.2.2求解器参数确定

因求解目标是端面液膜压力场，故采用压力速度耦合下的SIMPLE算法[11-12]，采用一阶迎风式离散动量方程。端面液膜处于层流状态，黏性模式设置为层流。采用压力求解器求解模型，压力求解器以动量和压力为基本变量，通过连续性方程导出压力和速度，结合本次分析对象和计算要求，选择Segregated Solvers算法[3]。

3 机械密封端面流固耦合有限元分析

3.1 分析方法

焊接金属波纹管机械密封密封环端面处于混合摩擦状态，不仅受动、静环接触产生的内应力，还存在端面液膜流场所产生的液膜压力，应力场较为复杂。密封端面是机械密封最容易发生失效的关键部位之一，即使是端面所产生的微小变形，也会对机械密封的整体性能产生较大的影响，所以分析密封端面的准确变形对提高机械密封的密封性能、防止事故的发生有重要意义。端面变形会影响端面液膜压力，而液膜压力的改变也会影响端面的变形，两个不同场域的解分别是对方的输入。为了解决这类问题，采用流固耦合分析法对密封端面进行分析[13]。

目前流固耦合解算方式分为单向流固耦合和双向流固耦合。单向流固耦合分析单计算流体分析中的压力到结构分析中，或者单计算结构分析中的变形到流体分析中[14]。双向流固耦合分析区别于单向流固耦合分析，流场和结构场在同一时刻交换数据(流场输出压力变量、结构场输出变形变量)。综合考虑研究情况，需要流体网格同步固体网格的变化，且无大变形，不存在大变形带来的网格问题，故选择双向流固耦合分析法。

3.2 建模与网格划分

选择ANSYS Workbench软件中DM平台建立模型，机械密封动、静环组成的密封端面为轴对称结构，所受的力载荷和边界条件也是轴对称的，因此在ANSYS中按照轴对称问题进行求解，并将模型简化为周期模型。根据某公司提供的密封环原始尺寸简化后绘制二维CAD图形，在DM平台中建立三维实体模型，并导入MESH模块中划分网格，选择相应的三维结构实体单元SOLID 45进行仿真计算。建立的密封环有限元网格模型见图6。其中密封坝(密封宽度)为4 mm，静环外径为47.5 mm、内径为39.5 mm，动环外径为48.5 mm、内径为40.75 mm，载荷系数为0.75[15-16]。

图6 密封环有限元网格模型

3.3 载荷分布及边界约束

静环与补偿环座固定，视为全位移约束。动环嵌套在非补偿环座中，故在其径向位移施加约束，动环右端受弹簧载荷作用，径向环面受到法向介质压力作用。密封端面动、静环均受到液膜反力和接触力。根据某机械密封公司提供的实际工况条件，侧面承受1 MPa介质压力，可得端面比压p端=pt+p载-pm≈720 Pa (pt为弹簧比压，p载为介质压力，pm为摩擦比压)。

4 机械密封端面流固耦合计算结果分析

4.1 变形

密封环介质压力1 MPa、转速2 000 r/min、弹簧力136.5 N时密封环流固耦合变形结果见图7。由图7可知，整个密封环最大变形约为0.197 μm，出现在静环内侧拐点处，这是因为密封环最大应力集中在静环内侧拐点处。密封端面最大应力出现在静环内侧，是因为静环系L型结构，且静环端面受弹簧力作用形成悬臂梁力学模型。

图7 密封环流固耦合变形云图

沿半径在密封坝上取20个点的变形，在Excel中绘制得到密封坝端面变形沿半径的变化曲线，见图8。

图8 密封坝端面变形沿半径变化曲线

由图8可知，密封坝上最大变形出现在内径边缘，最小变形出现在外径边缘，并且变形量沿半径近似线性分布。这是由于摩擦生热产生的温度变化主要集中在密封坝处，靠近内径处温度最高，热膨胀变形量大，外径处温度低，热变形量小。

4.2 压力与流速

介质压力1 MPa、出口压力(设为大气压力)0.1 MPa、转速3 000 r/min下求解得到的端面液膜流体的压力分布图见图9。观察图9可知，端面液膜在外径处于高压区，在内径处于低压区，这是因为外径处介质压力较高，高压侧密封介质沿端面间隙进入密封环端面并向内径方向流动，在这个过程中压力逐渐降低直至内径处达到最小值。

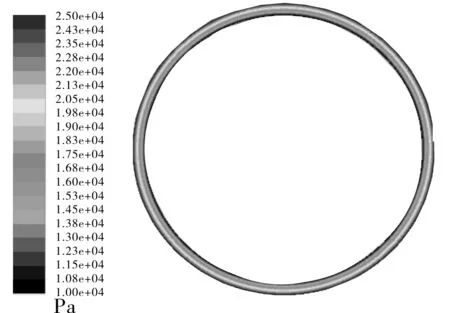
图9 端面液膜流体压力分布

介质压力1 MPa时密封端面平均压力与转速关系曲线见图10，转速2 000 r/min下密封端面平均流速、平均压力与介质压力关系曲线分别见图11、图12。

图10 介质压力1 MPa时密封端面平均压力与转速关系曲线

图11 转速2 000 r/min下密封端面平均流速与介质压力关系曲线

图12 转速2 000 r/min下密封端面平均压力与介质压力关系曲线

分析图9～图12，在介质压力不变、转速改变的工况下，端面液膜压力由外径向内径均匀降低，端面平均压力随转速的增高而缓慢增大，在1 000～3 000 r/min只有0.05 MPa的增幅，基本保持稳定。在转速不变、介质压力改变的情况下，液膜整体压力值随着介质压力的增大而增大，且增幅较大，这是由于在出口压力恒定的情况下，介质压力增大会导致流入密封端面的流体压力增大，液膜压力增大。所以介质压力是影响端面液膜压力场分布的决定因素，而端面流体平均速度随介质压力增加变化不大。

4.3 泄漏量

密封端面泄漏量随转速及介质压力变化曲线见图13和图14。由图13和图14可见，泄漏量与介质压力成正相关，但转速对它的影响可以忽略。

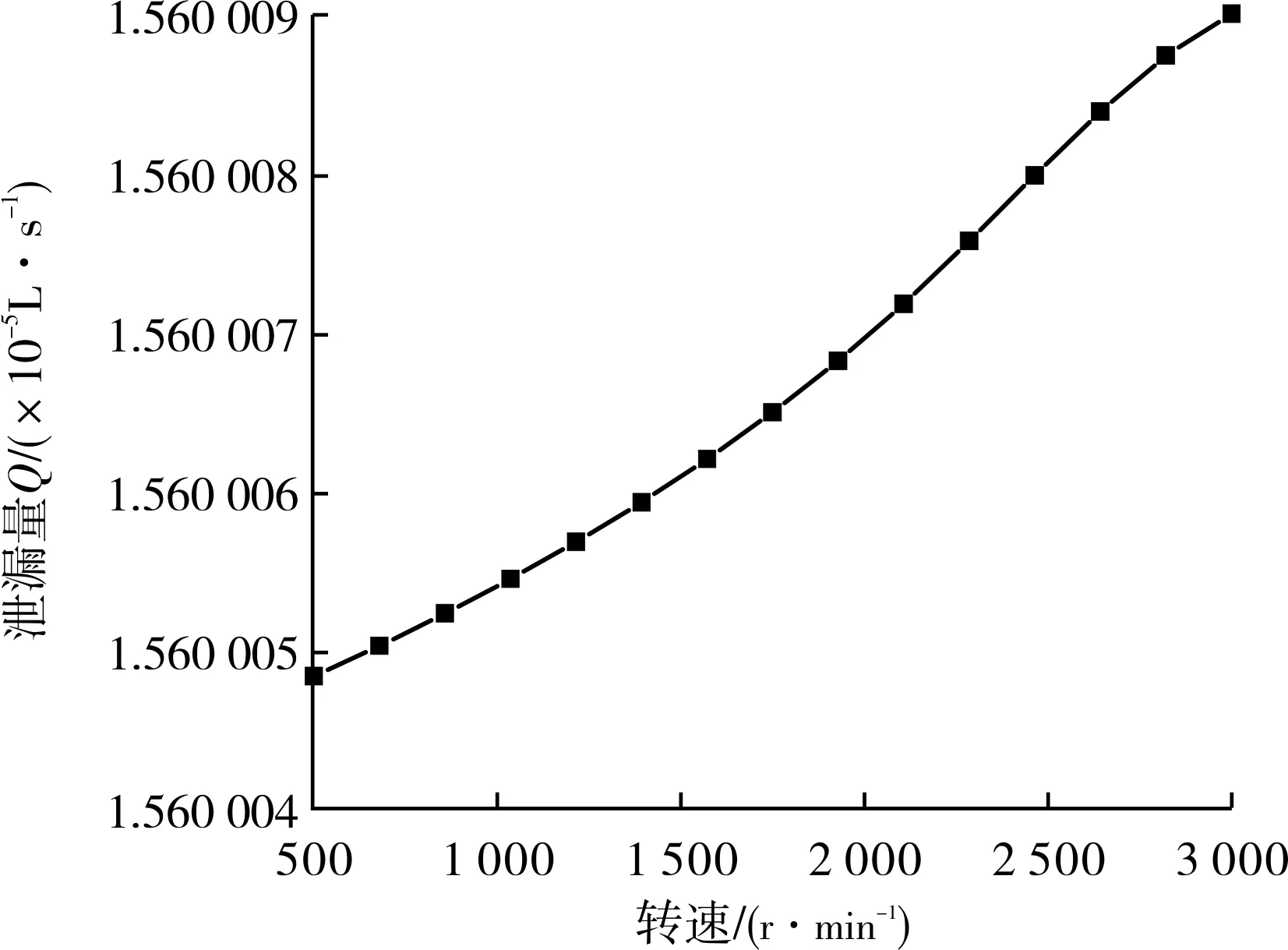
图13 密封端面泄漏量随转速变化曲线

根据对水平端面机械密封的研究，得到密封端面泄漏量的计算公式：

式中，Q为泄漏量，m3/s；dm为密封端面平均直径，m；Δp为密封端面液膜的内外压差，Pa；μ为液膜的动力黏度，Pa·s。

图14 密封端面泄漏量随介质压力变化曲线

5 结语

文中介绍了焊接金属波纹管机械密封端面密封性能的耦合分析，利用ANSYS Workbench平台建立了基于FLUENT的流体分析和ANSYS平台的静力学分析的耦合关系，研究了转速、介质压力对密封端面变形和端面泄漏量的影响。利用数值法很好地模拟了机械密封端面的密封情况，为端面密封研究提供了一种可靠有效的方法。