一种改进的病理显微图像亚像素快速配准方法

，

(华南理工大学 机械与汽车工程学院，广州 510641)

0 引言

图像配准是指求解两幅或者多幅具有相同场景或者内容的图像之间几何变换关系，图像配准是图像处理、机器视觉以及医疗成像中最重要的步骤之一[1]，医学图像拼接融合、计算机视觉领域的目标定位以及卫星遥感图像[2]等应用均对图像配准的精度有较高的要求。

扫描获取一张数字病理切片[3]通常需要进行数以千计的病理显微图像配准拼接，拼接过程中的图像对的配准是耗费时间的主要部分，由于病理切片对于医疗诊断有着极其重要的意义[4]，数字病理切片需要尽可能准确还原病理切片的所有信息，因而病理显微图像的快速高精度配准是获取高质量数字切片图像的最为关键一步[5]。

常见的医学图像的配准算法主要有以下几种：1)Appleton采用的互信息[6]等图像灰度区域信息配准方法，精度较高但配准速度慢；2)基于特征点的配准方法，彭勋所采用的改进SIFT算法[7]能够有效配准具有旋转、畸变等情况的图像，但特征点的筛选和匹配需要耗费大量计算，且在病理显微图像配准过程中出现的空白稀疏图像会导致特征点过少而配准失败；3)基于相位相关法[8]，通过将图像位移转换为图像频域的相位进行求解，相位相关法对光照变化不敏感，但是配准效率不高。

针对病理显微图像配准的应用特点，本文提出了一种新的快速配准方法。该方法利用对数差值函数对待匹配图像进行信息评估，并构建模板获取像素级粗定位，根据粗定位获取待配准子图，由相位相关法获取亚像素级细定位。

1 亚像素配准技术

1.1 归一化相位相关法

相位相关法主要是基于傅里叶变换中的平移定理，假设f1(x,y)和f2(x,y)是两幅存在平移变换(xs,ys)关系的图像，满足：

f2(x,y)=f1(x-xs,y-ys)

(1)

它们对应的傅里叶变换分别为F1(u，v)和F2(u，v)，则有：

F2(u,v)=e-j2π(uxs+vys)F1(u,v)

(2)

则f1(x,y)和f2(x,y)的归一化互功率谱为：

(3)

根据变换平移理论,互相关功率谱的相位等于两个图像的相位差,通过求互相关功率谱的傅里叶逆变换可以得到相位相关函数：

p(x,y)=F-1(ej2π(uxs+vys)=δ(x-xs,y-ys)

(4)

式中，δ(x-xs,y-ys)为典型的Dirac函数，也称为冲激函数，该函数在中心点(xs,ys)处不为零，在其他位置均为零。其坐标位置(xs,ys)即为图像平移量,由此得到了图像配准关系[9]。

1.2 基于相位获取亚像素配准技术

经典的相位相关法只能获取像素级精度的位移参数，为了进一步获取亚像素级精度的位移参数，常见的方法有以下几种：1)基于拟合的方法，利用正弦函数来逼近互功率谱的傅里叶逆变换所得的Dirac函数，再对拟合的谱函数进行上采样，从而获取亚像素的配准估计值[10]；2)基于相位差解析的方法，两幅存在平移变换的图像之间的相位差是一个2D锯齿函数，根据其角分量在两个轴上重复的周期数与平移参数所存在的解析关系即可获得亚像素平移参数；3)Smith提出对图像傅里叶变换后进行零填充(zero-padding)上采样[11]，再进行相位相关法求取亚像素配准值，但其计算资源的耗费巨大往往难以满足实时处理的需求。在此基础上，Soummer[12]等提出了基于矩阵乘法的傅里叶变换，该算法在像素级粗匹配值的一定邻域范围内进行k倍上采样，计算出精度为1/k的亚像素配准值。

2 改进的病理显微图像亚像素配准算法

基于矩阵乘法的上采样离散傅里叶变换虽然一定程度上避免了传统的零填充上采样方法在求取图像亚像素位移时的不足，但是在利用相位相关法求取像素级位移的过程中，其计算量会随着图像尺寸的增大而急剧变大，这对于尺寸较大的病理显微图像而言，求取像素级位移的计算量及算法所耗时间将非常大。并且，由于相位相关法只提取了两幅图像互功率谱中的相位信息，虽然减少了对图像本身内容的依赖，但同时又缺乏了对于病理显微图像配准拼接过程中对于信息量的评估，对于病理切片扫描过程中常出现空白的显微图像不能进行有效地规避，浪费了计算资源以及时效还可能导致错误的配准结果。为了充分利用局部上采样相位相关法在亚像素配准的有效性，又能使其更适用于病理显微图像的配准应用，本文提出采用一种由对数差值函数来评价显微图像信息量，由对数差值函数构建模板匹配，从而获取待配准子图完成相位相关亚像素配准，提高配准的速度。

2.1 对数差值函数

用i表示图像的像素灰度值，则其灰度值对数差值函数[13]为：

fls(I(x,y),I(x',y'))=Kln(I(x,y)/I(x',y'))=

Kln(I(x',y'))-Kln(I(x,y))=u[I(x',y')]-u[I(x,y)]

(5)

若i表示像素灰度值，则式(5)中：

u[i]=Kln(i)

(6)

对于常用的8 bit灰度图像，i∈[0,255]，ln(i)的值一般比较小，所以K为大于1的常数放大系数。当i=0时，ln(i)无效，为了处理方便，用一个极小常量ε(0<ε<<1)代替，即u[0]=Klnε。

对数差值函数有具备以下特性：

1)|fls(I(x,y),I(x',y'))|=|fls(I(x',y'),I(x,y))|,即表示对数差值函数值只与像素之间的灰度变化相关，与两像素点的先后次序无关；

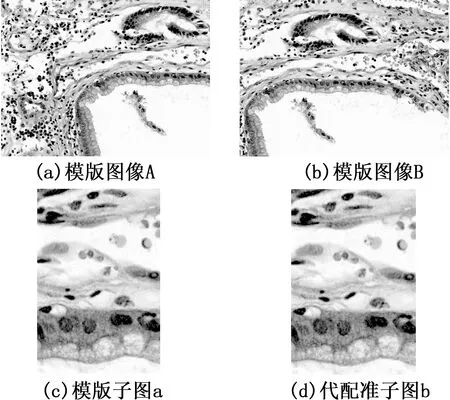
2)当I(x',y')>I(x,y)时，fls(I(x,y),I(x',y'))>0，即表示两像素间灰度值递增；当I(x',y')

3)I(x',y')与I(x,y)差异越小，|fls(I(x,y),I(x',y'))|越小；I(x',y')与I(x,y)差异越大，|fls(I(x,y),I(x',y'))|越大；即|fls(I(x,y),I(x',y'))|可以反映了两个像素之间灰度变化幅度的大小；4)u[i]的值可以预先计算并存在表格里，使用fls(I(x,y),I(x',y'))评价像素间的灰度变化幅度时只需要进行查表和减法运算，计算量很小。

2.2 病理显微图像亚像素配准算法的流程

第一步，构建H型对数差值模板。

以图像的左上角为原点O(0,0)，以水平向右为X轴正方向，垂直向下为Y轴正方向，H型对数模板由如图所示U、H、V三条线段组成，线段U和V的长度为l，线段H的长度为s。以线段U的第一个点P(x,y)确定模板的位置，线段H的第一个点坐标为P(x,y+m),则线段U上的像素依次为P(x,y+k),线段U上的像素依次为P(x+s,y+k),线段H上像素依次为P(x+n,y+m),k=0,1,…,l-1,n=0,1,…,s-1，下文中将线段U,V,H的各像素点的灰度值统一分别记为Ik,Jk,Dn,Ik,Jk,Dn∈[0,255],n=0,1,…,s-1,k=0,1,…l-1。

图1 H型对数差值模板

使用对数差值函数分别计算线段U和线段H上相邻两个像素间的灰度值变化,定义特征向量：

αlsp=(a0,a1,…,al-1)T=

(fls(I0,I1),fls(I1,I2),…fls(Il-2,Il-1))

(7)

γlsp= (y0,y1,…,yl-1)T=

(fls(D0,D1),fls(D1,D2),…fls(Dn-2,Dn-1))

(8)

计算获取线段U和V上对应位置像素间的灰度值变化，定义特征向量：

βlsp= (b0,b1,…,bl-1)T=

(fls(I0,I1),fls(I1,I2), …fls(Il-2,Il-1))

(9)

αlsp、βlsp和γlsp，共同组成H型对数差值模板Tlsp即：

Tlsp=(αlsp,βlsp,γlsp)

(10)

在病理显微图像配准中，图像A,B为有一定重叠区域的待配准图像对，在图像A重叠区域的搜索区域中，线段U为使|αlsp|获得最大值的线段，线段V为使|βlsp|取得最大值的线段，U和V之间的距离即为s。此时便构建了H型对数差值模板Tlsp(A)。线段U和V确定之后，线段H为平行线段U、V之间|γlsp|取得最大值的线段。

构建模板Tlsp(A)时要先确定l的参数，H型对数差值模板长度l应当小于待搜索区域，增加模板长度l可以有效提高配准精度，同时也会增加计算量，降低配准速度。因此，长度l应权衡速度与精度取适当的值。参数s,l为构建最佳匹配模板Tlsp(B(x,y))的必备参数信息。

第二步，图像信息量评估。

在切片数字化扫描过程中，由于高倍率的物镜成像和病理切片的特点，采集的显微图像时常会包含非常稀疏甚至空白的区域(如图2例子所示)，在此区域内进行配准会导致误匹配，所以在构建模板Tlsp(A)的过程中，通过遍历搜索|αlsp|、|βlsp|以及|γlsp|各自的最大值，同时也是对待配准区域的灰度变化信息量进行了评估。

其中|αlsp|反映了在待配准区域图像中长度为l垂直线段相邻像素灰度变化最大的幅度，|βlsp|反映了在待配准区域图像中长度为l平行线段对应位置像素灰度变化最大的幅度，|γlsp|反映了模板平行线段U、V范围内水平线段相邻灰度值变化的最大幅度。

对于显微图像重叠区域为空白或者稀疏区域时，|αlsp|、|βlsp|以及|γlsp|的值均较小，分别设置灰度变化幅度阈值THα,THβ,THγ来判定模板是否拥有足够丰富的信息量来满足匹配要求，当搜索所得|αlsp|、|βlsp|、|γlsp|有：

(11)

(12)

(13)

即表示在图像A的搜索区域范围内整体像素的灰度变化幅度小，可认定为是图像搜索区域范围内像素灰度值单调甚至为空白区域，无法提供足够的灰度变化信息构建模板Tlsp(A)完成配准，即便构建模板或者进行相位相关配准其配准结果亦不具备可靠性，应当返回信息量不足的错误配准信息。

第三步，进行对数差值模板匹配获取粗定位。

在图像A中创建模板Tlsp(A)之后,并经过信息量评估判定，便可在图像B的待搜索区域中搜索Tlsp(A)的最佳配准模板Tlsp(B)以获取像素级别的粗配准值。配准示意图如图3所示。

图3 匹配示意图

在显微图像B的待搜索区域内各点PB(x,y)依据模板Tlsp(A)的尺寸参数s和l构建H型对数差值模板Tlsp(B(x,y))，计算Tlsp(A)和Tlsp(B(x,y))的差异值。

|Tlsp(B(x,y))-Tlsp(A)|=μ|αlsp(B(x,y))-αlsp(A) |+

ω|βlsp(B(x,y))-βlsp(A) |+(1-μ)|

γlsp(B(x,y))-γlsp(A) |

(14)

其中，μ(0<μ<1)、ω(0<ω<1)为各特征向量差异值的权重值。

为了进一步减少计算量，设置阈值TOv过滤灰度变化幅度较小的匹配点,αlsp(A)中分量绝对值大于TOv的位置的集合为Cα,βlsp(A)中分量绝对值大于TOv的位置的集合为Cβ,则有：

|αlsp(B(x,y))-αlsp(A)|=∑i∈Cα|ai(B(x,y))-ai(A)|

(15)

|βlsp(B(x,y))-βlsp(A)|=∑j∈Cβ|bj(B(x,y))-bj(A)|

(16)

通过设置阈值TOv大小可以减少匹配点的数量，降低比较特征向量差异所需要进行的减法运算次数，从而加快搜索匹配模板的速度，但是TOv过大也会造成匹配点的减少，致使误配率升高，所以TOv的大小要在速度和精度考虑中取适中的值。

当Tlsp(A)和Tlsp(B(x,y))的差异值取得最小值时，该位置的Tlsp(B(x,y))就是Tlsp(A)的最佳匹配。从而可以获取显微图像A与B的像素级图像偏移值Δpixel=(xpixel,ypixel)。

第四步，获取待配准子图。

在获取了Tlsp(A)的最佳匹配Tlsp(B(x,y))之后，为了进一步校正以及获取亚像素级图像配准偏移值，根据模板定位坐标PA(x,y),PB(x,y)分别在显微图像A,B截取图像大小为Na×Na、完全包含模板Tlsp(A)、Tlsp(B(x,y))的子图a,b，l

经过第二步的图像信息量评估以及第三步的像素级粗定位，实际上是对两幅显微图像待配准区域的所有子图进行筛选，通过比值模板匹配获取粗定位，并截取其小范围子图作为亚像素配准的输入图像对，图像尺寸的缩小可以有效减小相位相关法计算亚像素偏移值的计算量。

第五步，获取亚像素级细定位。

对两幅待匹配子图a,b进行傅里叶变换并计算其相位相关归一化互功率谱,在两幅大小为M×N的子图计算所得的互动率谱的中心位置(xc,yc)附近范围构建大小为2c邻域，在此邻域区域内采用矩阵相乘计算互功率谱矩阵M(u,v)的K倍上采样局部互功率谱矩阵，其大小为cK×cK，矩阵形式为：

(17)

其中，X=[0,1…,cK-1]T-cK/2+xcK;Y=[0,1…,cK-1]T-cK/2+ycK;U=[0,1,…M-1]T-M/2;V=[0,1,…N-1]T-N/2；M'(U,V)为互功率谱矩阵M(U,V)的中心变换形式。

在第三步对数模板匹配正确获取像素级的偏移值的情况下，两幅待配准的相邻子图仅存在亚像素级偏移，将中心位置(xc,yc)的1.5×1.5像素大小的邻域作为细定位的搜寻区域，可以确保亚像素级的细定位峰值点在此范围之内。病理显微拼接算法的上采样倍率K=100，即细定位将在150×150区域内获取亚像素定位点，因而运动偏移量的配准估计精度可以达到0.01像素。通过求解式(17)的傅里叶逆变换即可获得显微图像A与B的亚像素级的图像偏移值Δsub=(xsub,ysub)。

因此，改进的病理显微图像亚像素配准的偏移量为Δ(x,y)为：

(18)

算法流程图如图4所示。

图4 病理显微图像配准算法流程图

3 实验结果与分析

3.1 实验平台

为了验证改进的病理显微图像配准方法的可行性、精度以及效率，在如图5所示的实验平台对切片标本采集图像进行了实验。实验平台主要由机械运动平台、图像采集系统及软件平台组成。PC主要配置为Intel Core i5-4440,4G内存，wndows7操作系统，算法测试软件使用Microsoft Visual C++ 2013开发。

图5 实验平台

3.2 实验一

为了验证改进的病理显微图像配准算法的精度，在实验平台上对由广东医学院病理教研室提供的体大息肉ESD标本采集图像尺寸大小为2448×2048的病理显微图像样例，经过10倍上采样，从中截取五组的偏移量不同的待匹配图像组，经由降采样后得到大小为640×480存在亚像素平移图像组(图6展示其中一组)。分别使用文献[12]中所提出的交互相关法和本文所提出的配准方法来对这五组相邻的病理显微图像进行配准。得出的配准平移估计值如表1所示。

图6 精度测试待配准显微图像组

由表1数据可知，相较于文献[12]方法，本文方法在计算图像的亚像素位移是对图像组子图进行矩阵乘法相位相关法所获取，对五组相邻图像配准的最大偏差为0.04，配准精度达到0.01像素，验证了该方法具备亚像素级配准精度，能够很好地满足病理显微图像高精度配准的需求。

3.3 实验二

为了验证改进的病理显微图像配准算法在实际配准应用的配准速度以及可行性，在实验平台上分别对体大息肉ESD标本采集两种不同图像尺寸相邻显微图像共80对，40对显微图像尺寸大小为800×600，水平方向上重叠区域大小在[520,544](像素)范围内波动；另外40对显微图像尺寸大小为2448×2048，水平方向上重叠区域大小在[1636,1650](像素)范围内波动。分别采用文献[12]算法与本文方法对80对显微图像进行配准，并将两种算法80次水平配准耗时进行对比，以此来比较两种算法的配准速度。两种算法分别进行80对病理显微图像的配准耗时如图7所示。图8为其中一组相邻显微图像以及它们的进行相位相关计算的两幅子图。

图7 两种方法配准80对显微图像耗时结果

从图7数据可以得知，对于尺寸大小为800×600的40对显微图像，文献[12]的方法配准平均耗时230.125 ms，本文方法配准平均耗时89.225 ms，速度提升1.5倍；对于尺寸大小为2448×2048的40对显微图像，文献[12]的方法配准平均耗时988.4 ms，本文方法配准平均耗时261.45 ms，速度提升2.7倍；本文算法速度相较于文献[12]方法有着明显提高。可见，随着图像尺寸的增大，文献[12]算法配准耗时急剧增大，而本文方法得益于模板匹配与子图的应用，配准效率有着明显的提升，这对于病理切片扫描需要经过数千次图像配准的应用需求有着重要的意义。选取的子图表明经过信息评估，H型模板避开了显微图像的空白区域提高了配准可靠性。

并将这80对显微图像按照计算所得的配准值进行配准拼接，检验改进算法的有效性。图9为其中一对显微图像的拼接效果图，拼接无明显错位，配准融合效果良好，黑边为两幅显微图像在垂直方向的波动。

图8 图像对比

图9 病理显微图像配准拼接结果

4 结语

针对病理显微图像快速高精度配准的应用，本文提出一种结合对数差值模板匹配和局部相位相关法的显微图像亚像素配准方法。并且针对病理切片扫描过程中时常出现的空白区域，通过信息量评估来进行规避。本文方法虽然在创建H型对数差值模板和匹配过程中增加了一定的计算量，但是由于对数差值模板的特性，仅是增加了查表和减法运算，并通过对关键点的筛选，进一步减少了计算量。其增加的计算量小于由图像尺寸增加而带来的相位相关法所增加的运算，因此改进的病理显微图像配准算法速度有明显提升。经实验验证，本文算法配准精度可达0.01像素，速度为相位相关法的3.7倍(图像大小为2448×2048)，且图像尺寸越大速度优势越明显。因此，改进的配准方法更适用于病理切片扫描过程中海量的大尺寸显微图像配准的应用需求。