高速列车受电弓气动噪声分析与降噪研究
,, ,
(上海工程技术大学 城市轨道交通学院,上海 201620)
0 引言
轨道交通发展的同时,人们对列车速度要求越来越高,加快了列车运行速度的提高,由于气动噪声的声压级增长速度是运行速度的6~8次方成正比[1-2],噪声问题日益突出。高速列车流线体外突出的部位与气流相撞,严重干扰气流,同时产生强大的远场空气脉动压力场,进而转化为气动噪声。因此对高速列车气动噪声特性研究有着重要意义,促进对后续气动噪声降噪的研究。
从近场、远场气动噪声看,受电弓是高速列车主要气动噪声源之一[3-5];张亚东[6]等对气动噪声贡献量进行预测,得出受电弓气动噪声贡献量最大的是碳滑板、平衡臂、弓头支架、底架、绝缘子等;SUEKI[7]等在受电弓处采用多孔材料,在360 km/h风洞试验运行下噪声减小1.9 dB;张亚东等[8]对受电弓开/闭口方式、导流罩结构、导流罩安装位置进行低噪声设计,得到远场声压级最多降低3.1 dB的最优设计方案;在风洞实验中,列车最显著的噪声源是转向架和受电弓[9]; T.Mitsumoji等[10]在弓头表面施加等离子激励器,得到该方法可降低弓头产生的窄频带气动噪声,Takehisa等[11]研究受电弓弓角表面的偶极子噪声源,并分析了在弓角表面穿孔来降低气动噪声的原理。因此研究高速列车受电弓的气动噪声特性,对气动噪声的降噪研究有着重要意义。
目前,高速列车受电弓的气动噪声的数值仿真研究较少,对受电弓气动噪声的声压级特性、声压级频谱特性以及在不同车速下气动噪声规律等特性了解甚少。为受电弓气动噪声降噪研究提供参考依据,本文利用大涡模拟与FW-H声学模型对不同车速下受电弓气动噪声特性进行研究分析。
1 计算模型
1.1 几何模型
本文以CRH380B型高速列车为研究对象,建立列车几何模型,模型由一节头车、一节中间车和一节尾车组成,头车和尾车外形相同,头车车顶有2个空调导流罩,中间车车顶有1个单臂受电弓和1个受电弓空腔,且受电弓底座安装在空腔内。本文主要研究对象为车顶受电弓,对列车模型进行适当简化,在仿真中简化下半部分车身、车底转向架等结构,采用完全封闭的外风挡。单臂受电弓模型是以CX-NG型受电弓为原型,保留主要部件,忽略紧固件等细小零部件。列车模型总长度L=76.5 m,宽度W=3.26 m,高度H=3.89 m。高速列车简化模型如图1所示。

图1 高速列车几何模型
1.2 计算域与边界条件
高速列车流场计算域长宽高分别为306 m、78.24 m、38.9 m,列车位于计算域中下方,列车头车距离计算域进口处1倍列车长(即76.5 m),尾车距离计算域出口处2倍列车长(即153 m),且列车与地面间的距离忽略不计。
计算域的进口设置为速度进口条件。计算域出口设置为零压力出口条件。高速列车下方边界设置为无滑移条件。高速列车表面设置为无滑移的固定边界。
1.3 网格划分
本文采用ICEM CFD软件进行网格划分。计算域采用混合网格划分,列车车身附近采用四面体网格划分,外域采用六面体网格划分,四面体域与六面体域之间的数据传递通过建立interface交界面。考虑到受电弓部位的压力变化,对受电弓进行局部加密,设置最大网格尺寸为20 mm;车身附近采用加密形式;外场最大尺寸1000 mm。网格划分单元总数约为4 412万。如图2中(a)(b)所示。

图2 网格
1.4 计算方法
本文先基于SST k-w模型进行稳态计算,再采用宽频噪声模型对受电弓气动噪声源进行识别;瞬态计算是以稳态计算结果作为初始值,再进行瞬态计算,瞬态计算采用大涡模拟,得到流场中边界脉动压力,再利用傅里叶变换将流场中时域脉动信号变换成频域信号。在稳态计算中,采用SIMPIC算法;在瞬态计算中,采用PISO算法,且本文气动噪声最高频率为5 kHz,设置时间步长1×10-4s,计算2 000个时间步,总计0.2 s,具体的参数设置如表1所示。本文计算过程在Fluent软件中完成。
为了计算在高速行驶下受电弓的气动噪声情况,选取受电弓为噪声源,在列车远场附近,分别确定A、B、C、D、E列作为气动噪声的19个噪声监测点,见图3所示。

图3 监测点位置图

表1 流场计算参数
2 数学模型
本文研究中采用大涡模拟方法来预测声源相关信息。大涡模拟(LES)控制方程为:
(1)
(2)
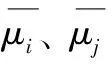
(3)
其中:μt为亚格子湍流粘性系数,表示如下:
(4)
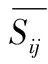
(5)
式中,Δ代表网格尺寸,Cs是Smagorinsky常数,对于大多数流动问题Cs=0.1具有较好的模拟结果。
由于LES只能进行瞬态计算,且对初始流场的要求比较高,从而需要进行稳态计算,稳态计算采用SST k-w湍流模型,其控制方程为:
(6)
(7)
(8)

式中,Ω为涡量,y为近壁面的距离,k为湍流动能,ω为湍流比耗散率,μt为湍流黏性系数,σk、σω、σω2、β为经验系数,ρ为密度,xj为方向坐标,μi为气流速度分量。
3 受电弓气动噪声特性分析
3.1 受电弓流场特性
图4为列车以350 km/h速度运行时,受电弓表面压力云图。有图4可知,碳滑板、弓头支架等表面的迎风面是正压,其中最大正压值为8 070 Pa,绝缘子背风面有最大负压,值为6 040 Pa。由于受电弓安装在车顶空腔内,底架及绝缘子迎风面受到的压力较小,在1 000 Pa左右。以轨道中心线为对称线,受电弓表面静压力表现出较大的对称性。
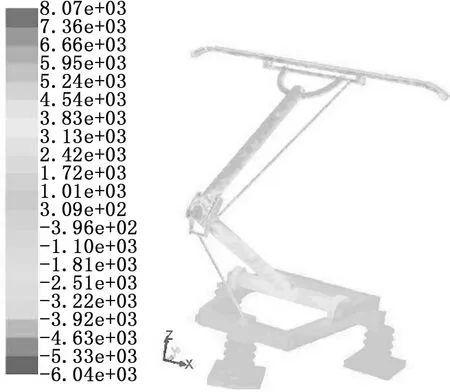
图4 受电弓表面压力云图
3.2 受电弓声场特性
在稳态流场计算结果的基础上进行瞬态计算,并建立噪声监测点,进行瞬态研究,将经过瞬态计算得到的噪声监测点的声压数据进行FFT变换,可得到监测点相应的声压级频谱曲线及1/3倍频程图。本文在受电弓附近设置5列噪声监测点(共19个监测点),高度与地面的垂直距离为3.5 m,每列从上到下依次为1、2、3等,如A列噪声监测点A-1、A-2、A-3,其中E列为远场标准监测点。噪声监测点设置位置如图3所示。
3.2.1 气动噪声声压级分布
图5为高速列车以速度为350 km/h运行时车顶表面声功率分布云图及受电弓部位的声功率级分布云图。由图可看出,在列车车顶部位,较大表面声功率级的部位为受电弓,表面声功率级值为111 dB。以轨道中心线为对称线,受电弓表面声压级有较强的对称性。受电弓碳滑板、弓头声功率级峰值达到100 dB以上,最大声压级为111 dB。当列车时速为200 km、250 km、300 km时,受电弓处最大声功率级分别为93.5 dB、102 dB、109 dB。由于受电弓表面声功率较大的地方其脉动压力值较大,产生较强的气动噪声,因此,受电弓碳滑板、弓头部位是受电弓产生的主要噪声源。

图5 车顶表面声功率及受电弓声功率分布云图
图6是E列7个标准监测点的气动噪声总声压级,由图可知,列车速度的增加,各监测点气动噪声总声压级也随之增加,200 km/h、250 km/h、300 km/h、350 km/h列车速度下平均总声压级分别为61.61 dB、65.16 dB、74.15 dB、78.02 dB,平均总声压级增加幅值为3.55 dB、8.99 dB、3.87 dB。当列车时速从200 km提高到350 km时,受电弓气动噪声传到远场各个标准监测点时,总声压级值最大相差分别为0.83 dB、1.46 dB、0.45 dB、0.15 dB。
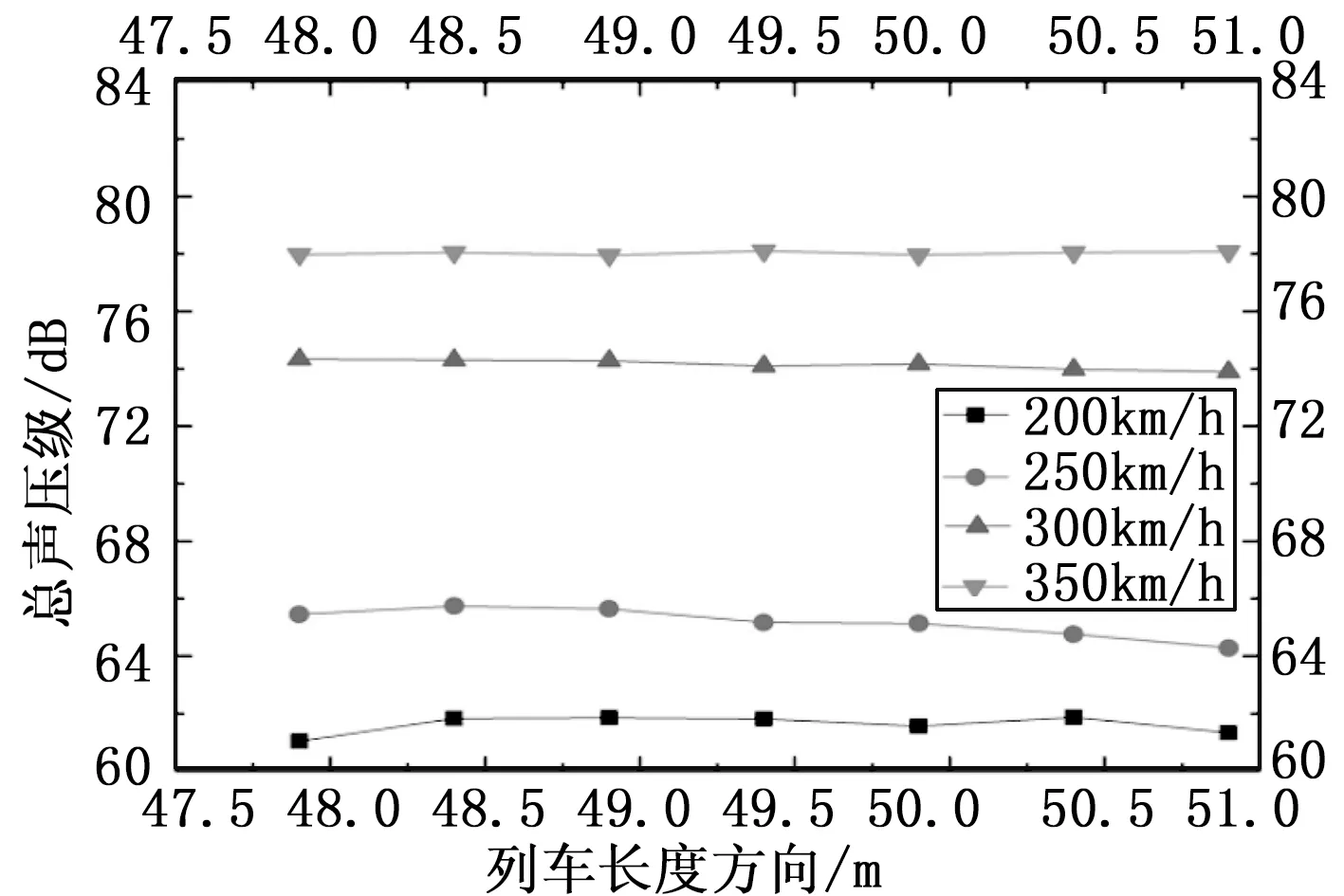
图6 E列监测点总声压级图
3.2.2 气动噪声频域分布特征
图7为仿真得到的以轨道中心线对称的A、B、C、D四列监测点在高速列车在300 km/h下的声压级频谱图,从图中可得出如下结论:
(1)所有噪声监测点的声压级随频率的变化规律基本相同,声压级分布的频带较宽,声压级幅值在低频段时较高,各个噪声监测点的声压级随着频率的增加呈现出下降的趋势。由此可知该型高速列车受电弓产生的气动噪声是一种宽频噪声。
(2)由图10以及表3总声压级值可知,列车左右两边对称的监测点频谱曲线图有较强的重合,以轨道中心线为对称线,表现出较强的对称性。

图7 对称监测点声压级频谱图
图8为列车在不同速度下运行时,距离地面高3.5米处,y=49米截面上,距离轨道中心线不同距离的A-2、B-2、E-4监测点总声压级图。由图可看出,在同一车速下,离轨道中心线的距离逐渐增大,监测点的气动噪声总声压级逐渐减小。各车速下总声压级减小的幅值在6.07~11.56 dB,且在不同车速下相邻两监测点的总声压级减小的幅值在0.01~0.93 dB。
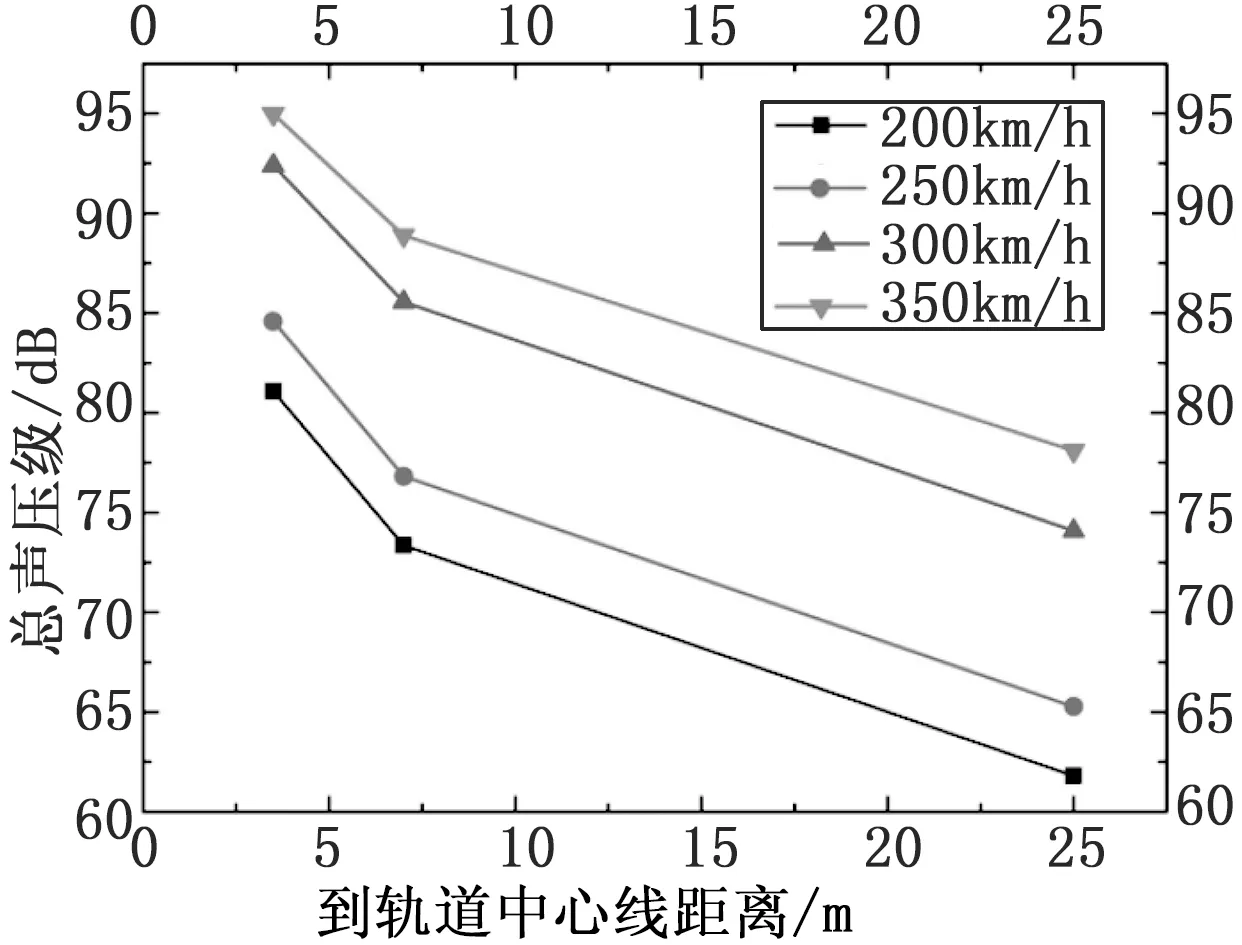
图8 列车横向监测点声压级图
由表2可知,在列车速度为250 km/h下,距离轨道中心线从3.5 m增加到25 m,其气动噪声声压级减小的幅值为7.76 dB(A)、11.65 dB(A),在不同列车速度下气动噪声声压级最大减小的幅值分别为11.56 dB(A)、11.65 dB(A)、11.47 dB(A)、10.80 dB(A)。

表2 列车横向监测点A计权声压级 dB(A)
3.2.3 A计权声压级1/3倍频程分析
A计权声压级是模拟人耳对55 dB以下低强度噪声的频率特性,和人耳的听感特性最为相似贴切,图9为列车在不同速度下运行时,监测点1的A计权声压级1/3倍频程图。由图可看出:

图9 不同速度下监测点A-2的1/3倍频程频谱图
(1)随着列车运行速度的增加,A计权声压级也随之增加,且主要能量集中在500~5 000 Hz频域内,最高A计权声压级值也逐渐增大。
(2)随着1/3倍频程的增加,监测点气动噪声A计权声压级也随之迅速增加,在0~500 Hz频率范围内,气动噪声的A计权声压级随着1/3倍频程的增加而迅速增加。
(3)列车速度为200 km/h、250 km/h、300 km/h、350 km/h时,主要能量分布在4 500~5 000 Hz,4 200~5 000 Hz,1 400~1 800 Hz,1 600~2 000 Hz,存在明显的主频,随着列车速度的增加,主频有着从高频向低频移动的趋势。
表3所示为各个监测点在不同速度下的总声压级值。
4 受电弓降噪研究
4.1 气动噪声降噪方法
高速列车气动噪声的产生及传播属于流体动力学领域,受电弓部位气动噪声降噪主要分为两大类,分别为被动降噪和主动降噪。其中,被动降噪是没有外部能量输入,目前主要靠优化几何结构、材料属性、安装导流罩、仿生改形设计、受电弓开/闭口方式等来改变流场,这些被动降噪对气动噪声只能达到有限的降噪效果;主动降噪是由外部能量输入,直接作用在局部流场中,来改变局部流场,从而达到降低气动噪声的目的,其中T.Mitsumoji等在弓头表面施加等离子激励器,得到该方法可降低弓头产生的窄频带气动噪声。

表3 不同列车速度下监测点总声压级对比表 dB
对大型客机起落架气动噪声进行主动降噪的,有如下几种方法,高哲采用空气膜降噪法,在原本形成湍流的区域增加额外层流(空气膜),层流代替原来不规则的流动,使湍流区域明显减小;任旺在起落架背风面边缘施加垂直射流,使射流、扭力臂与支柱构成一近似封闭空间。
4.2 受电弓降噪分析
空腔噪声产生的机理是由于,气流流经空腔前缘产生分离,在空腔上方形成剪切层,转化为漩涡运动,漩涡以一定的速度流向空腔下游,到达空腔后缘处与空腔后壁产生碰撞,从而诱发向前传播的压力波。
为改变空腔内的湍流,在高速列车受电弓空腔背风面设置射流降噪装置,射流面是宽为400 mm,长为2200 mm的矩形。射流温度与来流温度保持一致,射流在整个面上保持速度均匀分布,速度设置为30 m/s,列车速度为97.2 m/s。射流方向位置如图10所示。

图10 射流位置图
在建立的受电弓模型附近设置1个噪声监测点,位于空腔的中部,高度与车顶保持一致。图11给出了该噪声监测点的A计权1/3倍频程图,从图11中可得出如下结论:
该监测点在降噪前脉动压力的能量较为稳定,主要分布于105~111dB(A)之间,在800 Hz时脉动压力级出现较高峰值,800 Hz之后的高频段变化幅值较小,趋于稳定。而在射流降噪后,噪声监测点在低频时迅速增加,然后趋于稳定,在800 Hz时脉动压力级出现最大幅值,900 Hz之后的高频段变化峰值较小,施加射流后,监测点计算得到的总声压级值从133.17 dB降到117.97 dB,该射流方法具有一定的降噪效果,为后面的降噪研究提供一定的基础。
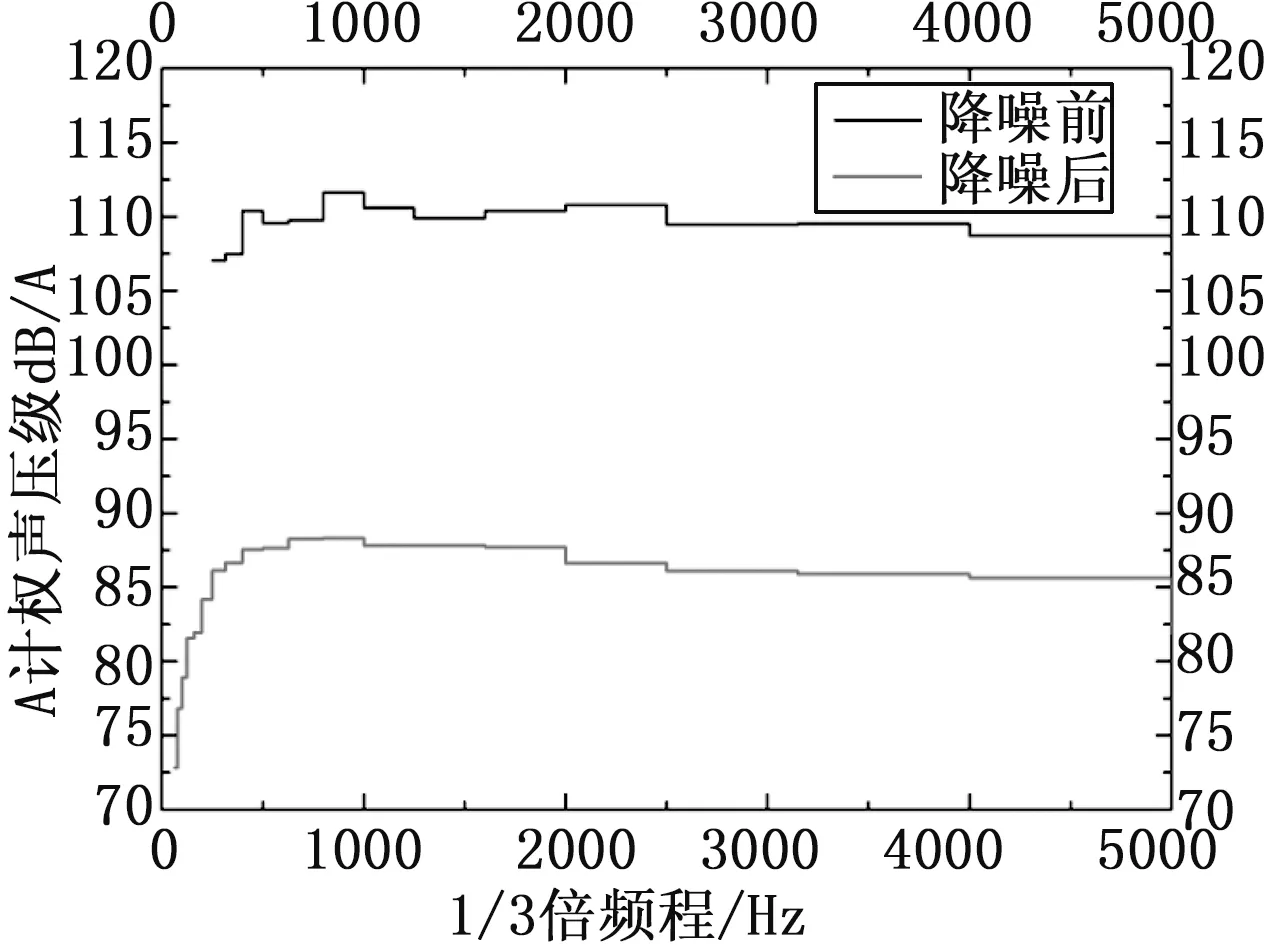
图11 监测点1/3倍频程图
5 结论
本文基于Lighthill声学理论,采用SST K-W模型、LES等模型对高速列车受电弓进行仿真模拟,并考虑不同列车运行速度,分析了受电弓的主要气动噪声源和远场气动噪声特性,并对受电弓进行降噪研究。基于仿真结果分析,可以得出以下结论。
(1)CRH380B高速列车车顶的主要气动噪声源是受电弓,受电弓部位的碳滑板、弓头等为受电弓的主要噪声源。
(2)高速列车以不同速度运行时,同一监测点随着列车运行速度的增加其声压级增加,以轨道中心线为对称的,监测点声压级及频谱特性表现出较高的对称性。
(3)高速列车以一定速度行驶时,随着离轨道中心线距离的增大,监测点的声压级逐渐减小,且在不同运行速度下,声压级降低的幅值相差较小。高速列车远场气动噪声是一种宽频噪声,其主要的能量集中在500~5000 Hz,存在明显的主频。
(4)在受电弓空腔处加射流主动降噪,监测点降低了15.2 dB,具有明显的降噪效果,为后续射流降噪研究提供基础。

