跨声速嗡鸣诱发机理及其失稳参数研究
高传强, 张伟伟
(西北工业大学 航空学院, 陕西 西安 710072)
0 引 言
现代高速飞行器有可能发生操纵面嗡鸣,通常表现为操纵面绕其刚轴不衰减的单自由度自激振荡,一般发生在跨声速及低超声速飞行范围内。嗡鸣问题是高速飞行器设计和使用过程中的拦路虎,其导致的大幅长时间振动,将会造成操纵面的损坏或严重变形,影响飞行安全[1-3]。
Tijdeman[4]根据激波在翼型表面的强度和位置将激波的运动分为A、B和C三种形式。其中A、B型主要发生于跨声速流动,激波还没有到达翼型后缘,不同的是A型流动激波仅在主翼上运动,操纵面处于激波引起的分离区中,而B型流动的激波强于A型,已经位于操纵面上;C型属于低超声速流动,激波更强,已经完全占据翼型表面。借鉴这种划分方式,跨声速嗡鸣(单自由度颤振)也通常被分为A、B和C三种类型。对于全动舵面模型,A、B型嗡鸣通常不再严格区分,其来流马赫数一般为0.7至0.95之间,C型嗡鸣来流马赫数依然为低超声速区,一般为M=0.96~1.6。
早在1947年, Erikson[1]等就对跨声速嗡鸣现象作了较详细的实验与理论分析,认为嗡鸣与翼型上表面产生的激波以及激波的前后晃动有关;激波的运动与舵面的振动之间存在相角差,该相角差被认为是嗡鸣产生的主要原因[5-7]。该观点逐渐被学术界和工业部门广为接受。Steger[8]等首先通过数值仿真方法验证了激波的运动与操纵面的振动间的相位滞后现象,国内的诸多学者[9-13]也通过数值仿真手段验证了上述结论。相位滞后解释的本质是气动力负阻尼效应,可以归结为能量的观点,即气流对结构做功。然而,所有的颤振问题都可以通过该观点解释,这显然不是嗡鸣的最突出特征。通过气动力负阻尼也不能解释嗡鸣为什么往往在特定的流动状态(跨声速“凹坑”区底部,与跨声速抖振边界有一定相关性)和结构参数(有限的操纵面旋转固有频率范围内)下发生,而这些才是飞行器设计师最关心的。
作者在近期的研究中通过CFD/CSD(Computational Fluid Dynamics/Computational Structural Dynamics)时域耦合仿真和降阶模型方法,开展了A型嗡鸣的失稳特性及其诱发机理研究。CFD/CSD仿真表明A型嗡鸣仅发生在抖振边界以下有限的迎角范围内,系统响应特性在抖振边界上下并没有发生突变,最终都达到一个相似的极限环振荡[14]。这说明这类嗡鸣与跨声速抖振密切相关,对前人的猜测给出了具体的数值论证。进一步的降阶模型分析研究表明A型嗡鸣的诱发与跨声速流动稳定性降低(跨声速抖振)密切相关,其本质是模态耦合引起的单自由度颤振,但是与结构间模态耦合引发的经典弯-扭耦合颤振不同,此时的单自由度颤振是结构模态与最不稳定流动模态耦合引发的[15]。其中的流动模态表征流动的本构特征及其稳定性特性,可以通过降阶模型方法获得其对应的特征值。
以上研究虽然给出了A型嗡鸣触发的流动条件,但是依然没有给出结构频率参数上下界明确的物理意义,同时也没有对B型和C型嗡鸣开展研究。因此,本文通过CFD/CSD耦合仿真和气动弹性降阶模型分析两种途径探究跨声速嗡鸣触发的本质原因,并给出嗡鸣发生的流动条件和结构条件。
1 研究模型及方法
1.1 研究模型
本文拟通过全动舵面为例探究三类嗡鸣的诱发机理,研究模型采用俯仰支撑的NACA0012翼型。对于全动舵面,A/B型嗡鸣不再严格区分,当马赫数或迎角较大时可以认为是B型嗡鸣,而当马赫数或迎角较小时是A型嗡鸣。
研究模型的示意图如图1所示,其中结构参数为无量纲质量比μ,俯仰支撑频率kα和支撑轴位置a。流动参数考虑来流马赫数M和来流迎角α。
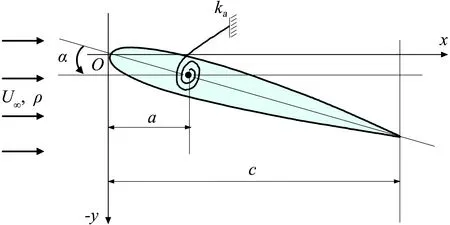
图1 研究模型示意图Fig.1 Sketch map of the research model
对于图1中所示的单自由度俯仰运动翼型,结构运动方程可以分别表示为:
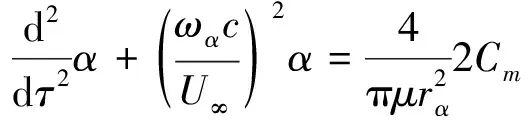
(1)
1.2 研究方法
本文拟分别采用CFD/CSD耦合仿真和基于ROM(Reduced Order Model)的气动弹性降阶模型研究系统的耦合特性。
在CFD/CSD耦合仿真方面,气动力的获取通过求解URANS(Unsteady Reynolds Averaged Navier Stokes)方程获得,空间离散采用迎风型的二阶AUSM+UP格式,时间推进采用双时间步法。湍流模型为SA模型。结构运动方程的求解通过具有四阶精度的四阶杂交的预估-校正方法,校正步中的广义气动力采用外插技术之后,气动力部分将由隐式格式退化为同阶精度的显示格式。该方法只需在预估步求解一次非定常流场,保证精度的同时求解效率大幅提高[16]。同时运用基于径向基函数插值的方法实现网格的变形。
除了时域仿真方法,本文还通过数据辨识方法构建了气动力降阶模型。辨识数据的输入为翼型的俯仰角度,输出为力矩系数,通过CFD(Computational Fluid Dynamics)方法计算翼型的强迫运动获得。将气动力降阶模型和结构运动方程模型在状态空间耦合,得到如下的气动弹性分析模型:
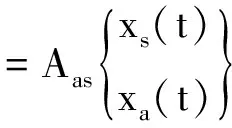
(2)
其中,下标a表示气动方面的量,下标s表示结构方面,如xs表示结构状态向量,xa表示气动状态向量。这样,耦合系统的稳定性分析就转化为矩阵Aas特征值问题。通过求解不同结构参数(kα和μ等)下状态矩阵Aas的特征值,根据根轨迹图来分析相关参数对结构模态和流动模态的耦合特征及各自稳定性的影响。矩阵特征值的实部为耦合系统的阻尼系数,虚部为耦合振动频率。当阻尼系数大于零时,系统稳定;反之,系统发散。
2 分析与讨论
2.1 A/B型嗡鸣
作者首先通过降阶模型方法,针对A型嗡鸣的发生条件和失稳特性进行了细致的研究[15]。相关结果表明A型嗡鸣的诱发与跨声速流动稳定性降低(跨声速抖振)密切相关,其本质是模态耦合引起的单自由度颤振。研究还发现这种模态耦合失稳的发生需要具备两个条件,一是流动模态的阻尼必须足够小,二是结构固有频率与流动特征频率满足一定的相对关系。图2给出了Ma=0.7,α=4.5°来流条件下,不同结构参数下(质量比和结构减缩频率)系统失稳边界和失稳响应的频率特性,ks-f表示耦合响应频率,其中失稳上界为0.42,下界约为0.17,与该状态下的流动特征频率接近,但是受质量比影响较大。因此,频率边界的物理意义还有待进一步确认。
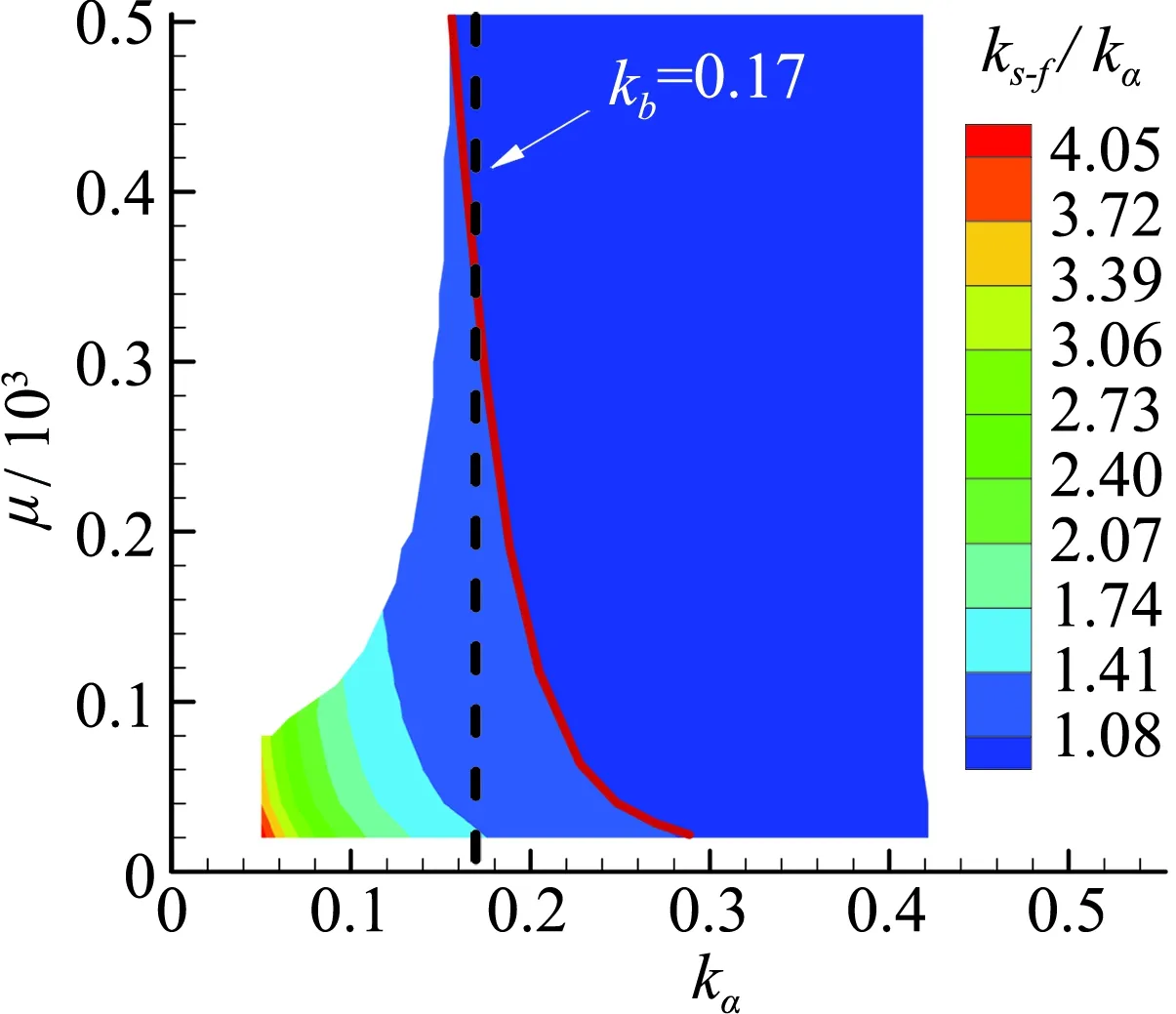
图2 不同质量比下失稳边界及响应频率分布,Ma=0.7, α=4.5°Fig.2 Instability boundary and coupling frequency as a function of mass ratio at Ma=0.7, α=4.5°
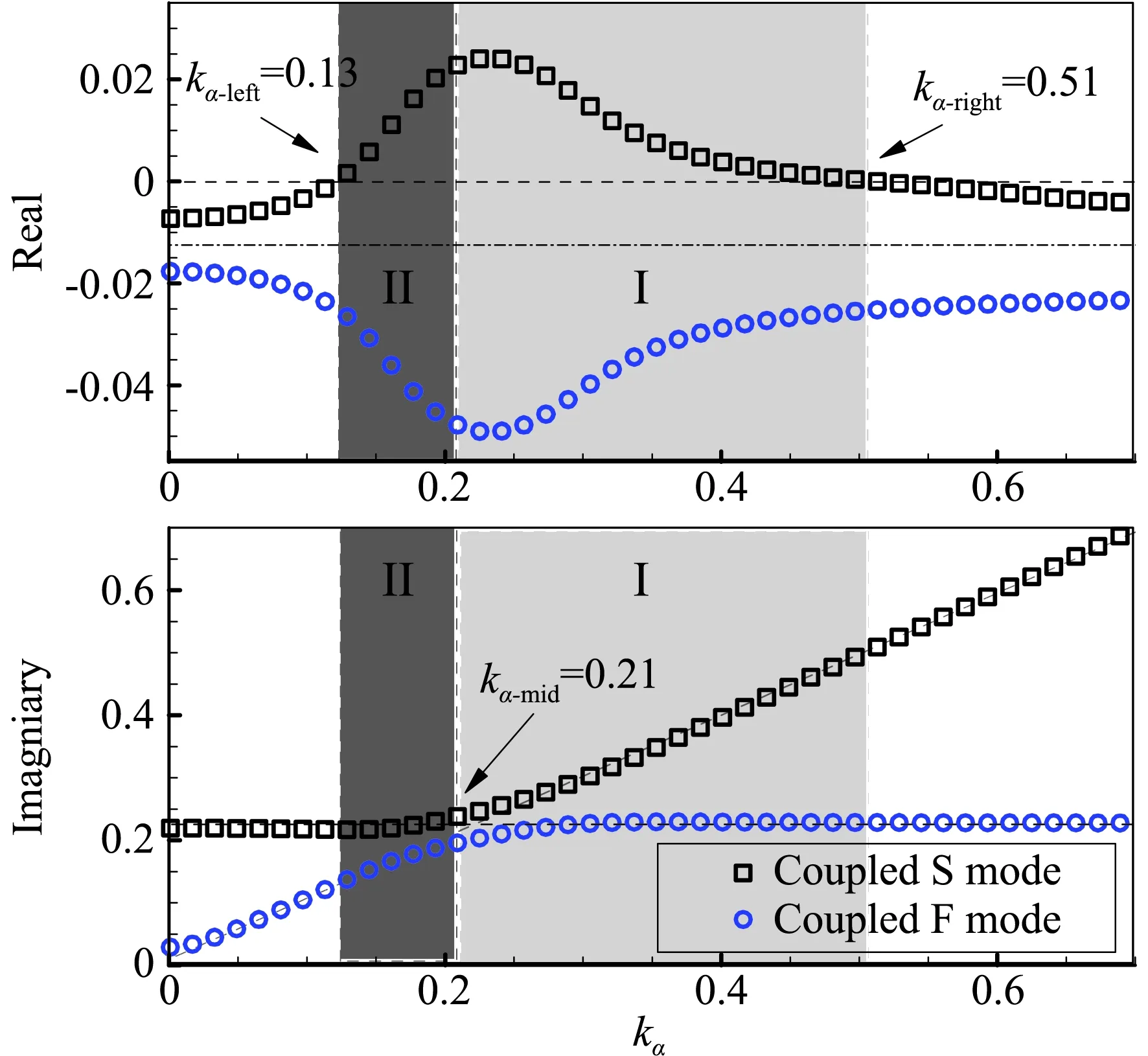
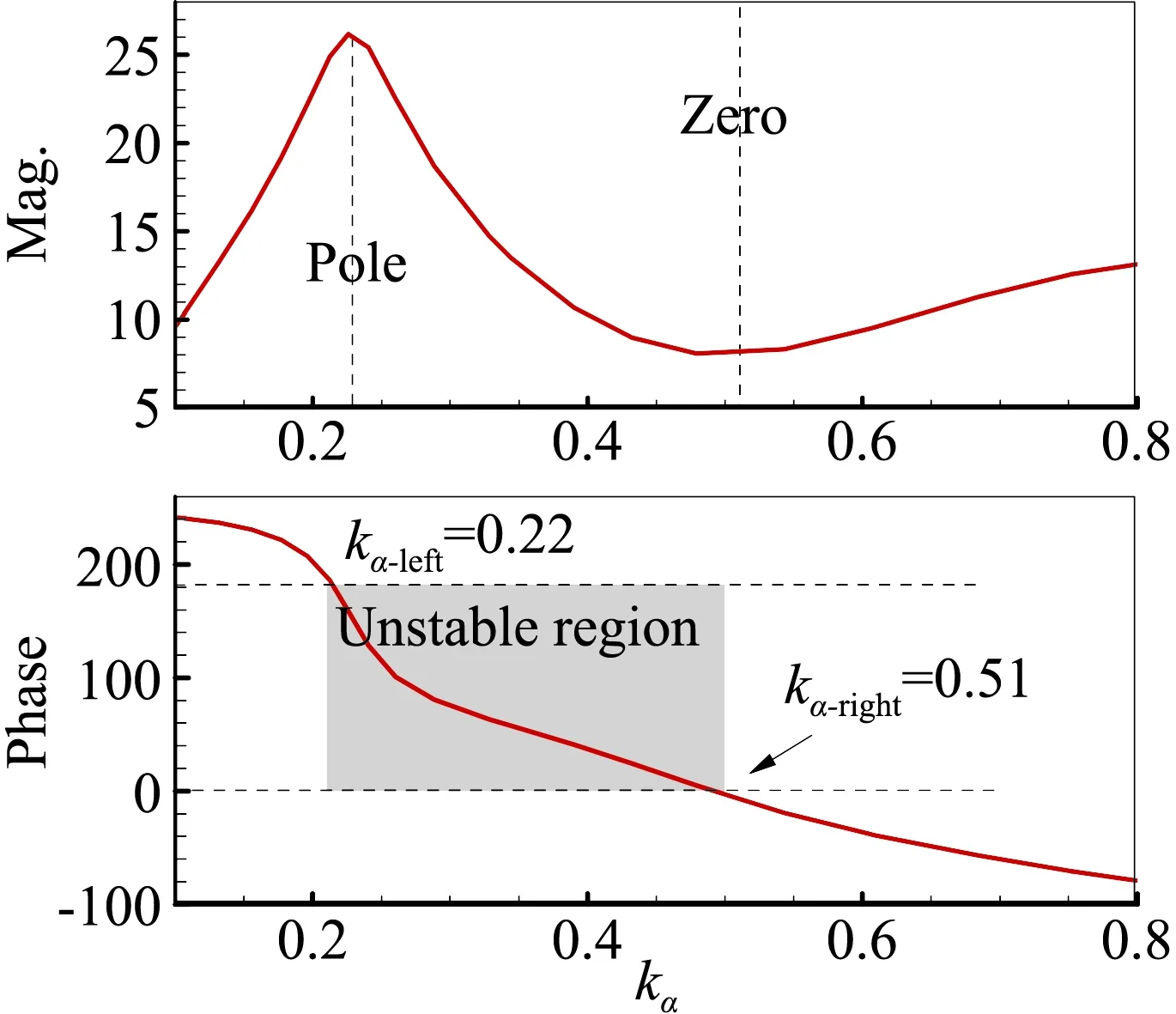
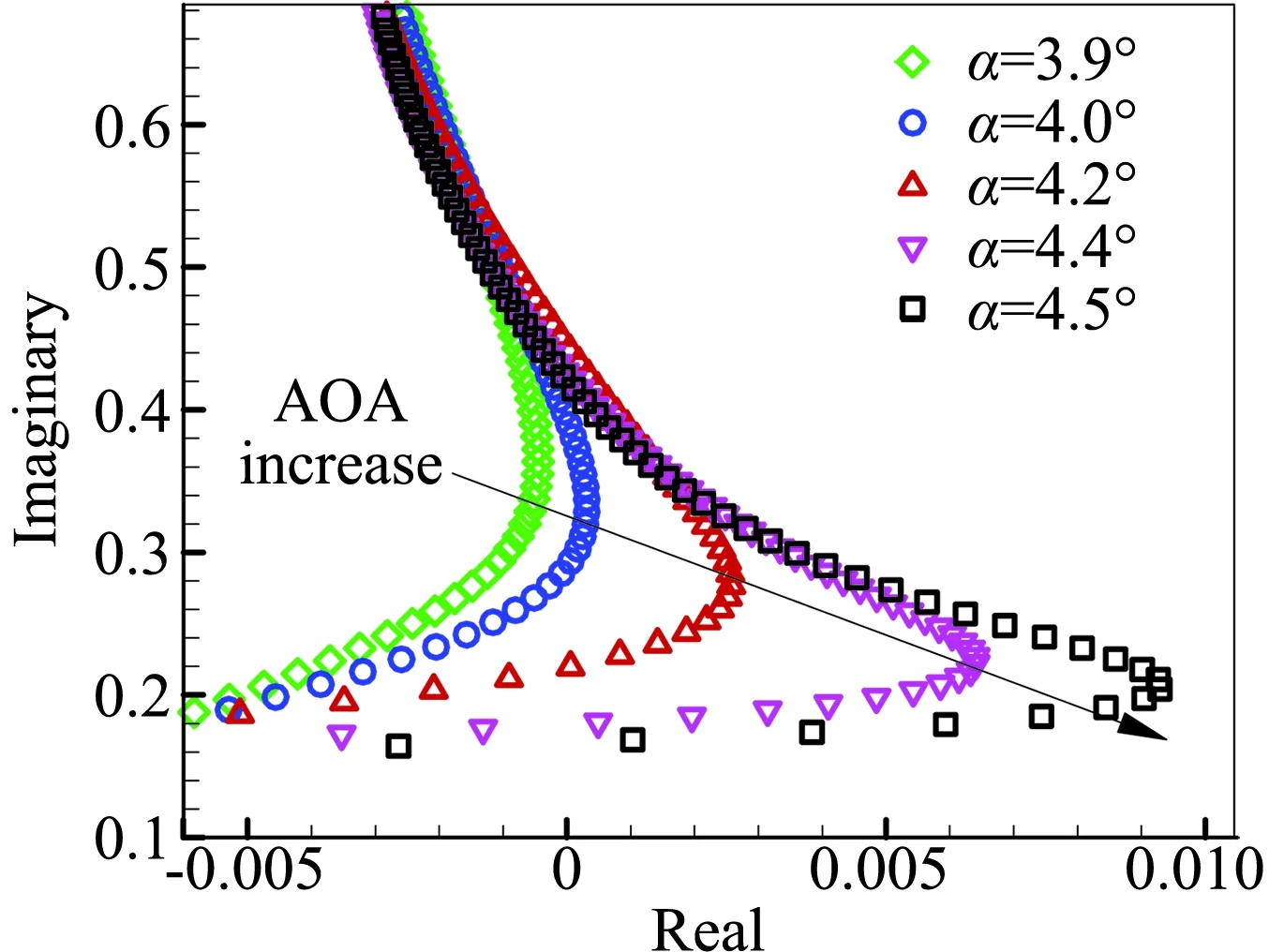
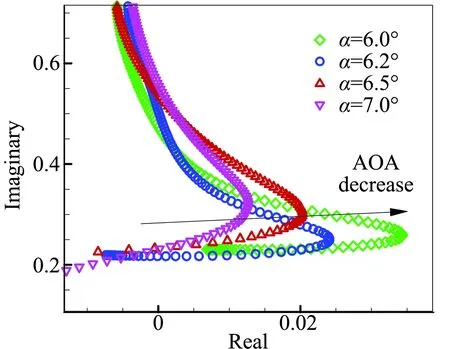
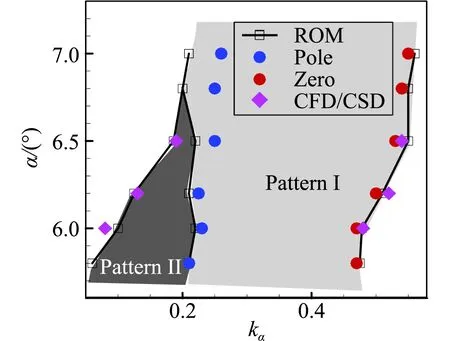
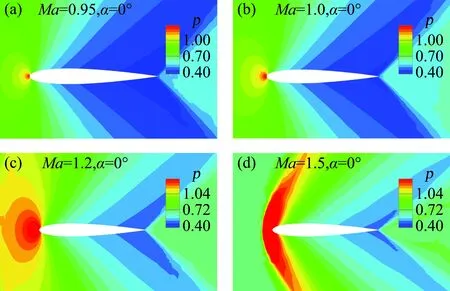
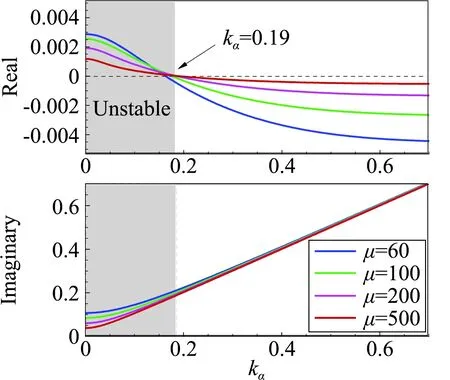
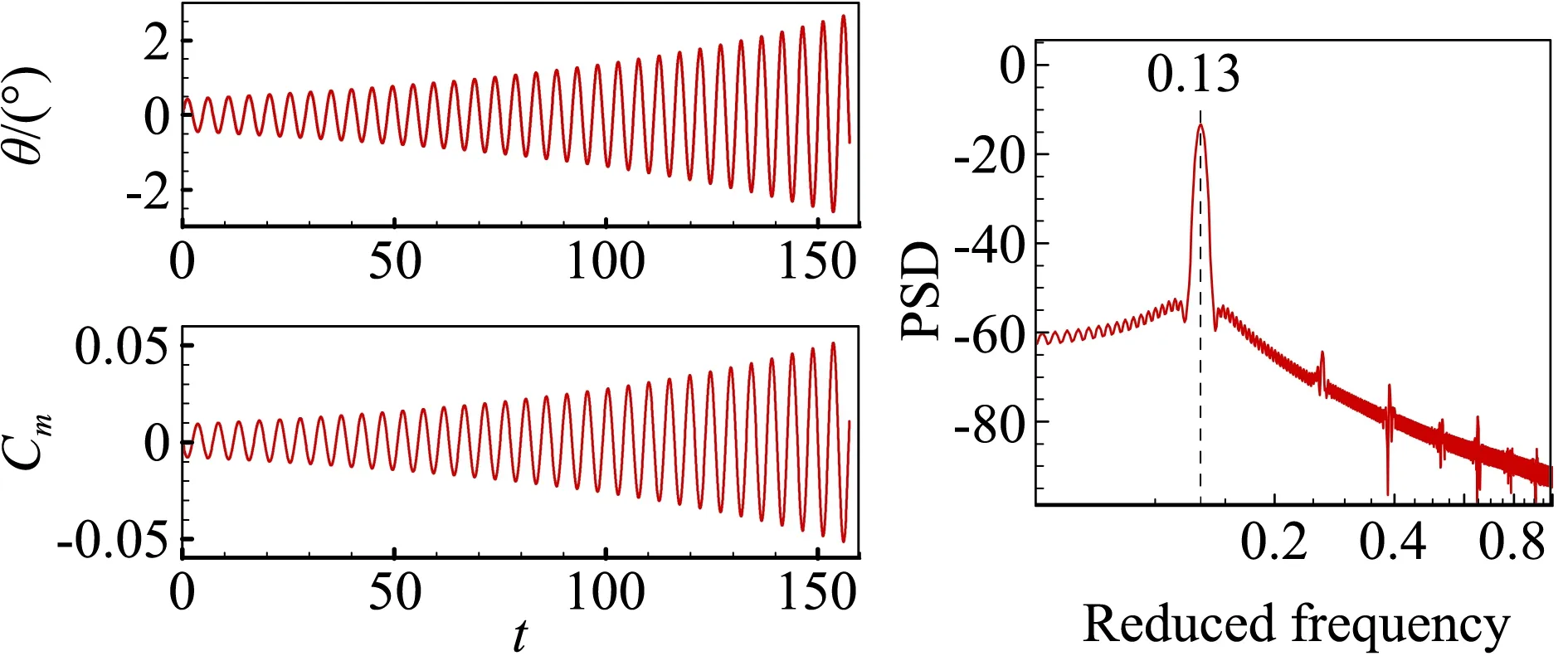
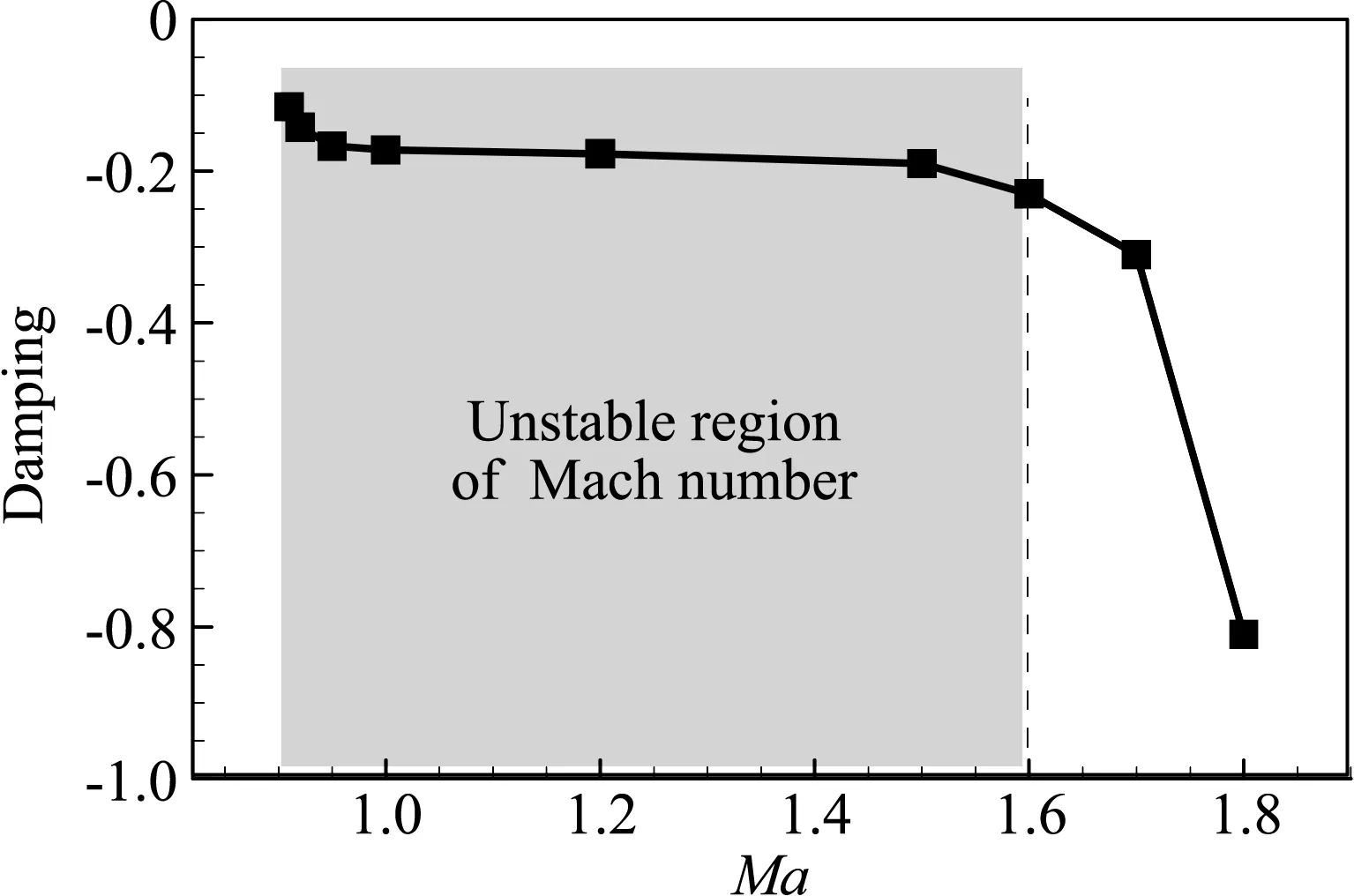
接下来我们将进一步探究频率失稳边界的物理意义,研究的来流状态如表1所示,其中的流动主模态特征根通过气动力降阶模型获得[17-18]。由NACA0012翼型的抖振特性可知Ma=0.7时抖振的始发和退出迎角分别是αonset=4.8°和αoffset=5.8°。这表明除了在抖振始发迎角附近 (α<αonset) 存在亚临界稳定区,在退出迎角附近(α>αoffset)也存在亚临界稳定区。图3给出了Ma=0.7,α=6.2°时,系统的特征值实部和虚部随结构频率的变化。可以看出特征值变化规律与α=4.5°的亚临界状态类似,首先根据频率特性确定各分支的模态属性,进而可将失稳区域分为模式I和模式II,其中模式II是抖振特性主导的失稳(具体特性见文献[19]),失稳范围为0.13 表1 典型研究状态(Ma=0.7)及其流动主模态Table 1 Typical cases and their dominant fluid mode (Ma=0.7) 图3 系统特征值实部和虚部随结构频率的变化,Ma=0.7,α=6.2°Fig.3 Real and imaginary parts of eigenvalue as a function of the structural frequency at Ma=0.7, α=6.2° 对比图3和表1,可以确定模式I的失稳下界由该状态下的流动主模态的特征频率决定。为了确定失稳上界的物理本质,图4给出了Ma=0.7,α=6.2°状态下开环系统的伯德图和其零极点分布。可以发现,伯德图的相频曲线预测的系统失稳范围与图3中的失稳区域完全一致,其中下边界kα=0.22对应幅频曲线中的极大值,表示系统的极点;而上边界kα=0.51对应幅频曲线中的极小值,表示系统的零点。该系统最不稳定零极点分布如图4(b)所示,相关特征频率与上述结果完全一致。此外,虽然系统极点是稳定的,但是零点是不稳定的,根据自动控制理论中的零极点关系可以确定,最终系统在极点频率和零点频率之间发生失稳。 (a) 伯德图 (b) 零极点 以上针对开环系统的伯德图和零极点的现象及分析也完全适用于表1中所示的其他状态。图5给出了抖振始发迎角和退出迎角附近若干来流状态下的根轨迹图比较,同时图6给出了失稳区域和零极点的比较。可以发现,两种状态下的根轨迹变化规律一致,在始发迎角附近,随着迎角的增加(靠近抖振始发迎角),系统失稳区域和强度都增大;类似的在退出迎角附近,随着迎角的减小(靠近抖振退出迎角),系统失稳区域和强度增大。这说明B型嗡鸣和A型嗡鸣类似,本质都是最不稳定流动模态与结构模态耦合导致的单自由度颤振,其诱发条件之一都要求该状态下流动的稳定性足够低,且流动稳定性越低,系统越容易失稳。另外,从图6对比发现,A型嗡鸣和B型嗡鸣中结构模态失稳的上、下边界分别由开环系统的零极点决定。这从根本上解释了失稳上界的物理意义,对研究嗡鸣的特性和工程中操纵面的防嗡鸣设计具有重要的指导意义。 (a) 抖振始发边界附近 (b) 抖振退出边界附近 (a) 抖振始发边界附近 (b) 抖振退出边界附近 Lambourne[3]通过理论模型预测C型嗡鸣可能发生的马赫数范围为0.96至1.4,在该范围内,激波运动的负阻尼效应导致结构的俯仰振荡。图7给出了Ma=0.95,1.0,1.2和1.5时的定常流场压力云图分布,可以发现这几个状态下激波已经完全到达翼型尾缘。论文将主要针对这几个典型状态讨论C型嗡鸣的失稳特性及其诱发机理。 图7 不同马赫数下流场压力分布Fig.7 Pressure distribution of flow field at different Mach numbers 首先研究C型嗡鸣的失稳特性。图8给出了Ma=1.2时降阶模型预测的不同质量比下系统特征根随结构频率的关系,其中俯仰轴位于0.15倍弦长处(a=0.15),质量比μ=60,100,200和500。与A/B型嗡鸣不同,从图8(a)中并不能提取出明显的参与耦合的流动特征模态,但是依然存在结构分支的失稳。失稳上边界为kα= 0.19,当kα< 0.19系统是不稳定的。另外,对比不同质量比的结果发现质量比对系统失稳区域几乎没有影响,这与文献结果及飞行试验数据类似。从图8(b)的特征值实部(阻尼特性)和虚部(频率特性)随结构频率变化关系可以看出C型嗡鸣的失稳阻尼很小,约0.001,较A/B型嗡鸣低一个量级左右,同时系统耦合频率始终近似跟随结构固有支撑频率。图9和图10分别给出了质量比μ=200下kα=0.16和kα=0.20时CFD/CSD仿真计算的时域响应及功率谱分析结果。首先,CFD/CSD仿真方法计算的失稳边界与模型预测结果一致;其次,时域响应的增幅率/衰减率表明系统的小阻尼特性;最后功率谱结果也与频率根轨迹预测结果一致。因此,本文的降阶模型方法能够准确预测C型嗡鸣的失稳特性。 (a) 根轨迹图 (b) 阻尼和频率变化图 图9 系统时间响应历程及功率谱分析,Ma=1.2,kα=0.16Fig.9 Time history and PSD analysis of the response at kα=0.16 图10 系统时间响应历程及功率谱分析,Ma=1.2,kα=0.2Fig.10 Time history and PSD analysis of the response at kα=0.2 我们进一步研究马赫数的影响。发现相关现象与Ma=1.2类似,只是具体的失稳范围不同。图11给出了Ma=0.89~1.8范围内系统的失稳区域,其中支撑轴固定于α=0.15,质量比μ=200。模型预测结果与CFD/CSD仿真结果几乎一致。研究发现,随着马赫数的增加,失稳范围逐渐减小,能够诱发C型嗡鸣的马赫数范围为0.91至1.6,这与Lambourne[3]预测的范围很接近。另外我们发现,稳定边界在马赫数为0.9附近发生突变,Ma=0.90时系统完全稳定,而当Ma=0.91时系统在较大范围内失稳。研究发现Ma=0.90时,激波位于0.95倍弦长附近,还没有完全到达尾缘,而当Ma=0.91时,激波已经完全到达尾缘。因此,激波拓扑结构的变化是造成系统稳定性在0.9马赫附近突变的根源。 图11 不同马赫数下系统失稳区域的比较Fig.11 Comparison of the instability region at different Mach numbers 接下来从流动模态的角度讨论C型嗡鸣的诱发机理。首先,图12给出了流动最不稳定特征根实部随马赫数的变化,在能够诱发嗡鸣的马赫数范围内,流动阻尼基本在-0.2附近。但是随着马赫数进一步增加(Ma>1.6),流动阻尼迅速减小,嗡鸣不再发生。因此,C型嗡鸣的诱发依然与流动在低超声速区稳定性裕量较低有关。然而,低超声速区流动的稳定裕量显然高于A型和B型嗡鸣所处的跨声速状态,因而C型嗡鸣中流动模态耦合较弱,失稳阻尼较低,表现为是一种缓和型颤振。因此,在工程中适当增加操纵系统的阻尼可以有效实现C型嗡鸣的抑制。图13给出了Ma=1.2时开环系统的伯德图和零极点分布,可以看出伯德图预测的失稳边界与CFD/CSD仿真结果一致,并且失稳上界频率与系统零点频率相同。因此,与 A/B型嗡鸣的失稳上界特性一致,C型嗡鸣的失稳上界也是由系统的零点频率决定。 A/B型嗡鸣和C型嗡鸣都是工程中常见的有限幅值的气动弹性问题,曾困扰很多工程型号的设计,现针对这两种嗡鸣的响应特性及诱发机理进行比较,具体的异同点如表2所示。 图12 不同马赫数下流动模态阻尼特性Fig.12 Damping characteristics of the dominant fluid mode at different Mach numbers (a) 伯德图 (b) 零极点 这两类嗡鸣具有许多类似的特点。首先,他们都是单自由度型的失稳颤振,表现为舵面/全动舵面有限幅值的振荡。从失稳特性来看,质量比(来流密度)对这两类嗡鸣影响较小,而对马赫数、迎角等较敏感。从失稳机理来看,他们都是流动模态和结构模态耦合造成的结构分支失稳,并且失稳频率范围由零极点频率决定。 表2 A/B型和C型嗡鸣的比较Table 2 Comparison between the A/B and C types of buss 但是同时两者又具有明显的差别。首先,从表面上看两种形式嗡鸣发生的流动状态不同,即来流马赫数和来流迎角不同。A/B型嗡鸣常发生在马赫数Ma=0.7~0.86范围内,往往具有一定的迎角,而C型嗡鸣发生在Ma=0.95~1.6范围内,一般零迎角状态即可发生。两者更深层次的不同体现在流动的稳定性不同,虽然两者都是本质稳定的流动,但是A/B型嗡鸣的流动的稳定裕量明显低于C型嗡鸣,从流动主模态对应的特征根的实部(阻尼特性)来看,两者相差10倍左右。这直接影响其与结构模态耦合形成的失稳模式的强弱, A/B型嗡鸣的失稳负阻尼较C型嗡鸣高一个量级左右。由于C型嗡鸣所处的流动的稳定裕量较大,流动模态的频率特征接近零频且不易捕捉,因而耦合系统失稳会发生在极小的结构频率状态下(对应极大的来流速度),类似土木工程中的驰振现象。从响应历程看,A/B型嗡鸣的振荡幅值较大,而C型嗡鸣在较小的振幅下就进入极限环状态,振荡幅值有限。 以上现象也决定了工程上对两类嗡鸣的改出措施是不同的。C型嗡鸣由于失稳负阻尼较小,很容易通过施加阻尼器的方式改出,而这种措施对A/B型嗡鸣并不太实用,因为往往需要施加足够大的阻尼才有效,这会造成操纵面对舵机指令响应的“迟钝”,不利于正常的飞行控制。A/B型嗡鸣主要通过提高舵轴的刚度改出,但是提高多少能够改出却没有具体的设计准则,实践中往往预留较大的刚度余量,付出的结构重量代价较大。 通过对嗡鸣的机理分析可以发现,流动模态的稳定性裕量是诱导嗡鸣发生和决定失稳特性的关键因素,因此,今后研究可以通过气动外形设计的方式设法提高流动模态的稳定裕量,进而从根本上抑制嗡鸣的发生,这种方式并不会增加结构复杂度和结构重量。 本文针对NACA0012翼型,通过CFD/CSD时域耦合仿真和基于ROM的气动弹性模型分析手段对三种类型嗡鸣的诱发机理及其失稳特性展开研究,得到如下结论: 1) 三类嗡鸣都是单自由度型的失稳颤振,本质是稳定性较低的流动模态和结构模态耦合造成的结构分支失稳; 2) A/B型嗡鸣发生在跨声速区,流动处于亚临界稳定状态(流动主模态阻尼足够小),这些状态往往在跨声速抖振始发和退出边界附近; 3) C型嗡鸣发生在低超声速区(Ma<1.6),其流动是稳定裕量明显大于A/B型嗡鸣的流动状态。 4) 嗡鸣诱发的结构支撑频率边界由系统的开环极点和零点对应的频率决定,因此,零极点频率是防嗡鸣设计中需要规避的关键频率; 5) C型嗡鸣的失稳负阻尼极小,比A/B型嗡鸣低近一个量级,因此,工程实践中施加阻尼器可以有效消除C型嗡鸣,而A/B型嗡鸣则难以消除。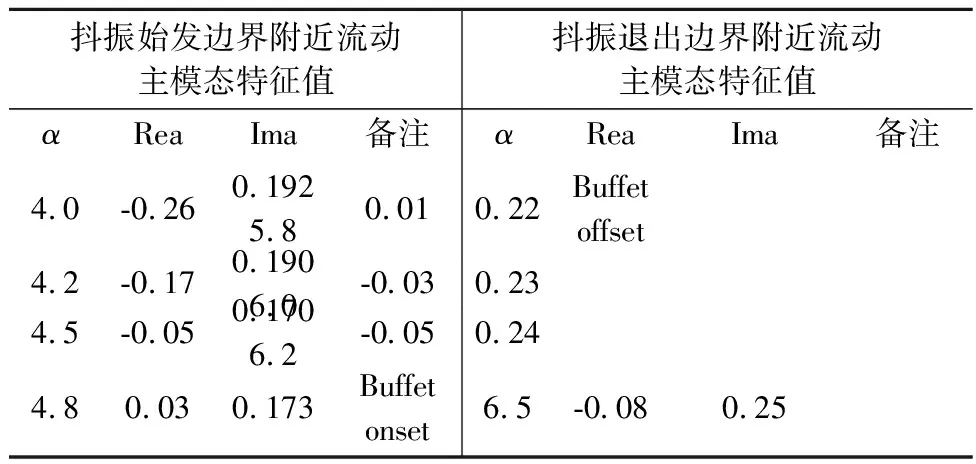


2.2 C型嗡鸣



2.3 A/B型和C型嗡鸣的比较和讨论



3 结 论

