飞翼布局无人机腹襟翼气动设计研究

, ,

(中航工业第一飞机设计研究院, 陕西 西安 7100891)

0 引 言

20世纪80年代，美国B2隐身轰炸机的问世标志着飞翼布局发展到了成熟阶段。近年来，飞翼布局以其特有的气动、结构和隐身优势，受到了无人机设计领域的高度重视[1]。美国是研究飞翼布局较早的国家之一，相继推出了X-45、X-47等系列低可探测性无人作战飞机研制计划[2-3]。与常规布局相比飞翼布局隐身性能好，巡航升阻比高，结构重量轻[4-5]；但是，飞翼布局飞机没有常规的平尾、垂尾，航向稳定性和操纵性较差[6-7]，俯仰操纵力臂较短，要获得与常规布局等效的俯仰操纵效果，需付出较大的升力损失[8-9]，飞翼布局飞机在起飞着陆阶段增升装置下偏增升的同时，将会产生较大的附加低头力矩，不满足起降操纵要求[10]。

为了提高飞翼布局无人机的起降气动性能，本文引入了一种安装在无人机下表面的腹襟翼装置[11]，打开腹襟翼可以增加飞机起降阶段的实用升力系数和俯仰力矩系数，能够改善飞机的起降性能。

近年来，国内外对腹襟翼开展了初步研究。Yann D. Staelens和Ron F. Blackwelder等人分别从试验和计算的角度简单研究了腹襟翼对飞翼布局飞机起降性能的影响[12-13]。Daniel Dougherty、Adam Vore和Hamid Hefazi对腹襟翼安装位置和尺寸的影响进行了试验研究[14]。康辉论述了腹襟翼对飞翼布局无人机的影响[11]。北京航空航天大学的张曙光等人通过飞翼布局小型验证机的飞行试验，验证了腹襟翼能够提高飞翼布局无人机的着陆安全性[15]。西北工业大学的沈冬等人对腹襟翼进行了二维的相关研究工作[16]。本文采用基于有限体积法的RANS方程，研究分析了腹襟翼对飞翼布局无人机起降气动性能的影响，并对腹襟翼的安装位置、偏角和板面实度进行了详细的气动优化设计研究。研究结果表明，打开腹襟翼能够增加起飞离地迎角的升力系数和俯仰力矩系数，从而提高了飞翼布局无人机的起降气动特性，通过对腹襟翼关键参数的气动优化设计研究，得到了最优的参数组合。

1 腹襟翼的工作原理

如图1所示，腹襟翼是安装在飞机腹部的一种增升和俯仰控制装置。图2给出了腹襟翼绕流的流场示意图，由图可见由于腹襟翼的存在，当气流流经飞机下表面时，使得腹襟翼前区域气流速度减小，因此该区域承受的压力增大，腹襟翼后区域流动出现分离，因此该区域承受的压力减小。

图1 腹襟翼示意图Fig.1 Diagram of the belly-flap

图2 腹襟翼绕流示意图Fig.2 Diagram of flow around the belly-flap

图3给出了压力变化对气动力影响的示意图，飞机下表面腹襟翼前后压力的改变对飞机产生了附加的抬头力矩，这种附加的抬头力矩对飞机起降阶段的俯仰力矩配平以及俯仰控制是有利的。

图3 腹襟翼工作原理示意图Fig.3 Diagram of working principles of the belly-flap

2 计算方法验证

本文数值模拟研究采用的是基于有限体积法的三维定常RANS方程求解器，湍流模型选择的是SA模式。

三维积分形式的雷诺平均N-S方程：

式中：V为控制体体积，S为控制体表面积，Q为守恒量，f为通过表面S的无黏通量和黏性通量之和，n为控制体表面S的外法向单位矢量。

为了验证计算方法的可靠性，采用该方法对某民机翼身组合体风洞试验标模的气动特性进行了数值模拟研究，并将气动力特性的计算结果与实验数据进行了对比。模型的几何参数如表 1所示，模型的俯视图如图4所示。

表1 模型的几何参数Table 1 Geometry parameters of the model

图4 某民机标模的俯视图Fig.4 Top view of the civil aircraft model

计算网格为采用ANSYS-ICEM软件生成的结构化网格，网格量约为1200万， 模型表面网格和对称面部分网格如图5所示，表 2为计算网格的分布情况。

图5 模型的网格Fig.5 Grid of the model

机翼附面层展向弦向网格量第一层到物面距离165129572×10-6m

低速计算模拟状态与风洞试验状态一致，计算迎角为-5°到13°。图6和图7分别为模型的升力系数和俯仰力矩系数计算结果与实验数据的对比，图中实线为本文RANS方程的计算结果，红色矩形符号为风洞试验结果。由气动力特性的对比结果可以看出，计算结果与试验数据吻合良好，验证了本文计算方法的可靠性。

图6 升力系数计算值与试验数据的对比Fig.6 Comparison of lift coefficient between calculated value and experimental data

3 算例分析

为了研究腹襟翼对飞翼布局飞机起降气动性能的影响，本文对如图8所示三种计算模型进行了CFD数值模拟研究。其中，a构型(Model a)为干净构型；b构型(Model b)为起降构型；c构型(Model c)为腹襟翼打开的起降构型，c构型腹襟翼位于无人机下表面重心后距重心15%MAC(平均气动弦长)位置处，腹襟翼打开角度为90°。

(a) 干净构型

(b) 起降构型

(c) 腹襟翼打开的起降构型

计算网格同样为采用ANSYS-ICEM软件生成的结构化网格，以c构型为例，网格如图9所示，网格量约为1000万，网格分布如表 3所示。

图9 c构型的网格Fig.9 Grid of the model c

机翼附面层展向弦向网格量第一层到物面距离217129493×10-6 m

采用RANS方程求解器对如图8所示的三种构型进行了低速数值模拟研究，计算马赫数为0.2，计算高度为标准海平面高度。图10为随迎角变化，b构型和c构型相对a构型升力系数增量的变化曲线，图11为随迎角变化，c构型相对b构型升力系数和俯仰力矩系数增量的变化曲线。

图10 b构型和c构型升力系数增量的变化曲线Fig.10 Curve of CL increment of Model b and Model c

图11 c构型升力系数增量和俯仰力矩系数增量的变化曲线Fig.11 Curve of CL increment and Cm increment of Model c

如图10所示，与a构型相比，由于打开增升装置，b构型和c构型的升力系数明显增大；如图11所示，与b构型相比，迎角小于10°时，c构型升力系数有所增大，俯仰力矩系数有所增加。在起飞离地迎角(8°)处，c构型升力系数比b构型大0.024 4，c构型俯仰力矩系数比b构型大0.025 4。因此，与起降构型相比，打开腹襟翼能够提高飞机起飞离地迎角的升力系数和俯仰力矩系数，对飞机的起飞着陆是有利的。

截取如图12所示距对称面2 m的剖面，图13和图14分别为c构型和b构型在该剖面处的压力云图和流线图谱。与图14相比，图13腹襟翼前气动压力明显增强，腹襟翼后气动压力明显减弱，因此与b构型相比，c构型抬头力矩增大。图15为c构型和b构型在该剖面处压力分布的对比，如图15所示，同样可以得到c构型腹襟翼前后气动载荷的变化，且与蓝线相比，黑线腹襟翼前面积的增加量比腹襟翼后面积的减小量要大，因此，c构型比b构型升力系数大。

图12 剖面位置示意图Fig.12 Diagram of profile position

图13 c构型剖面压力云图和流线Fig.13 Pressure clouds and streamlines on the profile of Model c

图14 b构型剖面压力云图和流线Fig.14 Pressure clouds and streamlines on the profile of Model b

图15 剖面压力分布的对比Fig.15 Comparison of profile pressure distribution

4 腹襟翼气动优化设计

为了寻求适用于本文飞翼布局无人机最优的腹襟翼，本文对腹襟翼的弦向位置、偏角和板面实度参数进行了气动优化设计研究，为保证计算结果的可对比性，计算网格与上文c模型的数量和分布情况完全一致。

4.1 弦向位置气动优化

以起降构型为基准，如图16所示分别将腹襟翼安装在无人机起降构型重心后15%MAC、20%MAC、25%MAC、30%MAC和35%MAC位置处，研究腹襟翼的安装位置对无人机低速气动性能的影响。图17和图18分别为随迎角变化，在不同位置安装上腹襟翼的起降构型相对原起降构型升力系数增量和俯仰力矩系数增量的变化曲线，图19和图20为8°迎角时相对起降构型，随腹襟翼位置的改变升力系数增量和俯仰力矩系数增量的变化曲线。如图19和图20所示随安装位置不断后移，当地迎角的升力系数增量不断增大，但是俯仰力矩系数增量不断减小。

图16 腹襟翼安装位置示意图Fig.16 Diagram of belly-flap locations

图17 升力系数增量的变化曲线Fig.17 Curve of CL increment

图18 俯仰力矩系数增量的变化曲线Fig.18 Curve of Cm increment

图19 升力系数增量随腹襟翼位置变化的关系曲线Fig.19 Curve of CL increment with belly-flap locations

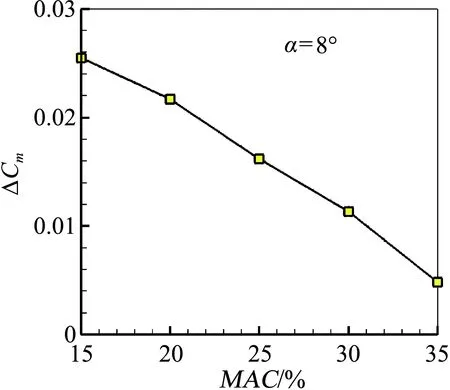
图20 俯仰力矩系数增量随腹襟翼位置变化的关系曲线Fig.20 Curve of Cm increment with belly-flap locations

由此可见,腹襟翼安装在重心后15%MAC和20%MAC位置，升力增量有限；安装在30%MAC和35%MAC位置，俯仰力矩系数增量有限。因此，权衡升力系数和俯仰力矩系数的增量，重心后25%MAC处为本文飞翼布局无人机腹襟翼的最佳安装位置。

4.2 偏角气动优化

选取重心后25%MAC处为腹襟翼的安装位置，研究腹襟翼的偏角对低速气动性能的影响，腹襟翼分别偏转30°、45°、60°和90°。图21和图22分别为随迎角变化，安装不同偏角的腹襟翼的起降构型相对原起降构型升力系数增量和俯仰力矩系数增量的变化曲线，图23和图24为8°迎角时相对起降构型，随腹襟翼偏角的改变升力系数增量和俯仰力矩系数增量的变化曲线。由图23和图24得到，在8°迎角时，随着腹襟翼偏角不断增大，当地迎角的升力系数增量和俯仰力矩系数增量都不断增大。因此，90°为本文飞翼布局无人机腹襟翼的最佳偏角。

图21 升力系数增量的变化曲线Fig.21 Curve of CL increment

图22 俯仰力矩系数增量的变化曲线Fig.22 Curve of Cm increment

图23 升力系数增量随腹襟翼偏角变化的关系曲线Fig.23 Curve of CL increment with deflection angles

图24 俯仰力矩系数增量随腹襟翼偏角变化的关系曲线Fig.24 Curve of Cm increment with deflection angles

4.3 板面实度气动优化

如图25在腹襟翼半模板面上设计了两个缝、四个缝和八个缝三种不同板面实度的腹襟翼模型，并分别安装在起降构型重心后25%MAC处，其中每个缝的形状和面积是相同的，保证每一种腹襟翼打开角度都为90°，研究腹襟翼板面实度对无人机低速气动性能的影响。

(a) 半模两个缝的腹襟翼模型

(b) 半模四个缝的腹襟翼模型

图26和图27分别为随迎角变化，安装不同板面实度腹襟翼的起降构型相对原起降构型升力系数增量和俯仰力矩系数增量的变化曲线，图中solid线为腹襟翼板面没有缝的计算结果；图28和图29为8°迎角时相对起降构型，随板面实度的改变当地迎角的升力系数增量和俯仰力矩系数增量的变化曲线，其中横坐标为腹襟翼半模板面缝的个数。如图28和图29所示，与其他模型相比，半模两个缝升力系数增量最大为0.057 9；未开缝模型俯仰力矩系数增量最大为0.016 19，因此，本文飞翼布局无人机腹襟翼的最优板面实度为半模开两个缝或者不开缝。

图26 升力系数增量的变化曲线Fig.26 Curve of CL increment

图27 俯仰力矩系数增量的变化曲线Fig.27 Curve of Cm increment

图28 升力系数增量随腹襟翼板面实度变化的关系曲线Fig.28 Curve of CL increment with the solidities

图29 俯仰力矩系数增量随腹襟翼板面实度变化的关系曲线Fig.29 Curve of Cm increment with the solidities

4.4 气动优化设计结果分析

通过上述腹襟翼的气动优化设计研究，得到了本文飞翼布局无人机最优的腹襟翼参数组合，即腹襟翼半模板面开两个缝或者不开缝，偏角为90°，且安装位置为无人机重心后25%MAC处。图30为腹襟翼最优的设计结果(板面不开缝)相对起降构型升力系数增量和俯仰力矩系数增量的变化曲线，在起飞离地迎角(8°)处，最优结果比起降构型升力系数大0.057，俯仰力矩系数大0.016 2。

图30 最优结果相对起降构型气动力特性增量的变化曲线Fig.30 Curve of aerodynamic characteristics increment of the optimal result versus the takeoff and landing configuration

5 结 论

本文采用基于有限体积法的三维定常RANS方程求解器，研究了腹襟翼对飞翼布局无人机起降气动性能的影响，并对腹襟翼的关键参数进行了详细地优化设计研究，有以下结论：

1) 通过对比研究飞翼布局无人机干净构型、起降构型和腹襟翼打开的起降构型三种模型的低速气动特性得到，打开腹襟翼能够提高飞机起飞离地迎角的升力和俯仰力矩，有利于飞机的起降；

2) 对于本文研究的飞翼布局无人机，腹襟翼安装在重心后25%MAC位置处，偏角为90°，且板面实度较大时对飞机的起飞性能最好。在起飞离地迎角(8°)处，最优结果比起降构型升力系数大0.057，俯仰力矩系数大0.016 2。