X形钢板剪力墙受力性能分析
,,,
(苏州科技大学江苏省结构工程重点实验室, 江苏苏州215011)
0 引言
传统结构在地震后残余变形过大,导致震后修复费用昂贵,或者无法修复。自复位结构(self-centering structure)作为一种新型的抗震结构,采用贯穿于梁的预应力钢绞线与柱连接,并辅助以耗能元件,从而实现地震时,耗能原件先于主体构件耗能,延缓结构主体损失进程,同时由于节点脱开,结构变柔,自振周期变长,从而减小基地剪力;地震后由预应力钢绞线提供恢复力,结构自动复位,减少了残余变形;最后通过更换耗能元件,实现震后可修。两边连接钢板剪力作为一种抗侧力构件,具有延性好,质量轻,耗能稳定且承载力高等优点,可以运用于自复位结构中[1]。
Clatyon[2,3]首先提出了薄钢板剪力墙自复位结构体系,并进行了试验研究。结果表明:1)利用薄钢板剪力墙其受水平荷载时的捏缩特征,能够实现结构的完全复位,大部分试件的残余位移角均在0.2 %以内。2)墙板越薄,复位效果越好。3)当墙板厚度一致时,两边连接墙板复位效果优于四边连接墙板,且更易震后更换。4)由于墙板采用了两边连接,拉力带未对柱产生附加弯矩,避免了结构主体先于耗能原件进入塑性的不利情况。5)自复位结构试验的滞回曲线可以近似看成自复位空框架与钢板剪力墙滞回曲线的叠加,在研究自复位耗能器时,通过耗能元件的滞回曲线可判断是否满足复位要求。Dowden[4]研究了在梁下翼缘开斜口,避免框架扩展现象的自复位节点,并考虑到应力集中对自复位节点的不利影响,提出在自复位结构中的钢板剪力墙应该在节点处开口,从而避免了自复位节点进入塑性。徐基磊等[5-12]提出采用角钢作为自复位结构中的耗能元件,结果表明,相比刚节点框架,震后残余位移角大幅度下降,复位效果良好,但由于耗能元件不提供刚度,结构整体刚度偏低,若采用增大构件截面的方法,则造价昂贵。
根据上述研究:自复位结构能够有效减少基底剪力,完全或大幅度减小震后结构残余变形;在自复位结构中,采用不提供额外抗侧刚度的耗能原件均有良好的复位效果,但结构整体刚度偏低,造价偏高;采用钢板剪力墙作为自复位结构中的耗能元件,在耗能的同时,能够提供额外抗侧刚度,减少自复位结构截面尺寸,但由于墙板的存在,为了使结构完全复位,需要增大钢绞线中的预应力,从而导致地震时,张拉节点过早进入塑性,不利于震后修复;此外,现有的钢板剪力墙自复位试验中,钢板剪力墙高厚比均在1000以上,当受循环荷载时,由于呼吸作用,墙板连续发出响声,容易引起业主恐慌,实际工程中难以运用。若采用厚板,其初始刚度大,耗能效果良好,但要实现复位效果则需要进一步加大预应力,梁的尺寸也要相应放大,造价不菲。根据以上结论,理想的自复位耗能元件要满足以下4点要求:①能够提供一定抗侧刚度。②耗能元件的滞回曲线捏缩,呈现剪切滑移特征。③稳定的耗能能力。④能够稳定提供承载力,且具有良好延性。
钢板剪力墙能够满足以上四点要求,相比于四边连接板,两边连接钢板剪力墙对拉力带约束较少,卸载时易提前发生失稳,从而在自复位结构中仅需要很小的预应力就能实现结构复位,因此可以采取减少拉力带约束的方法,在不降低承载力的同时,使钢板剪力墙更易卸载时失稳,从而适用于自复位结构。为此,本文提出削弱墙板腰部的X形钢板剪力墙,给出了墙板简化受力模型,分析了屈曲后墙板刚度突变原因,推导了墙板弹性刚度和承载力公式,考虑了不同跨高比和高厚比对墙板受力性能的影响规律,结合模拟给出了简化公式和破坏模式,并对比了矩形板和X板受压区对滞回曲线的具体贡献。
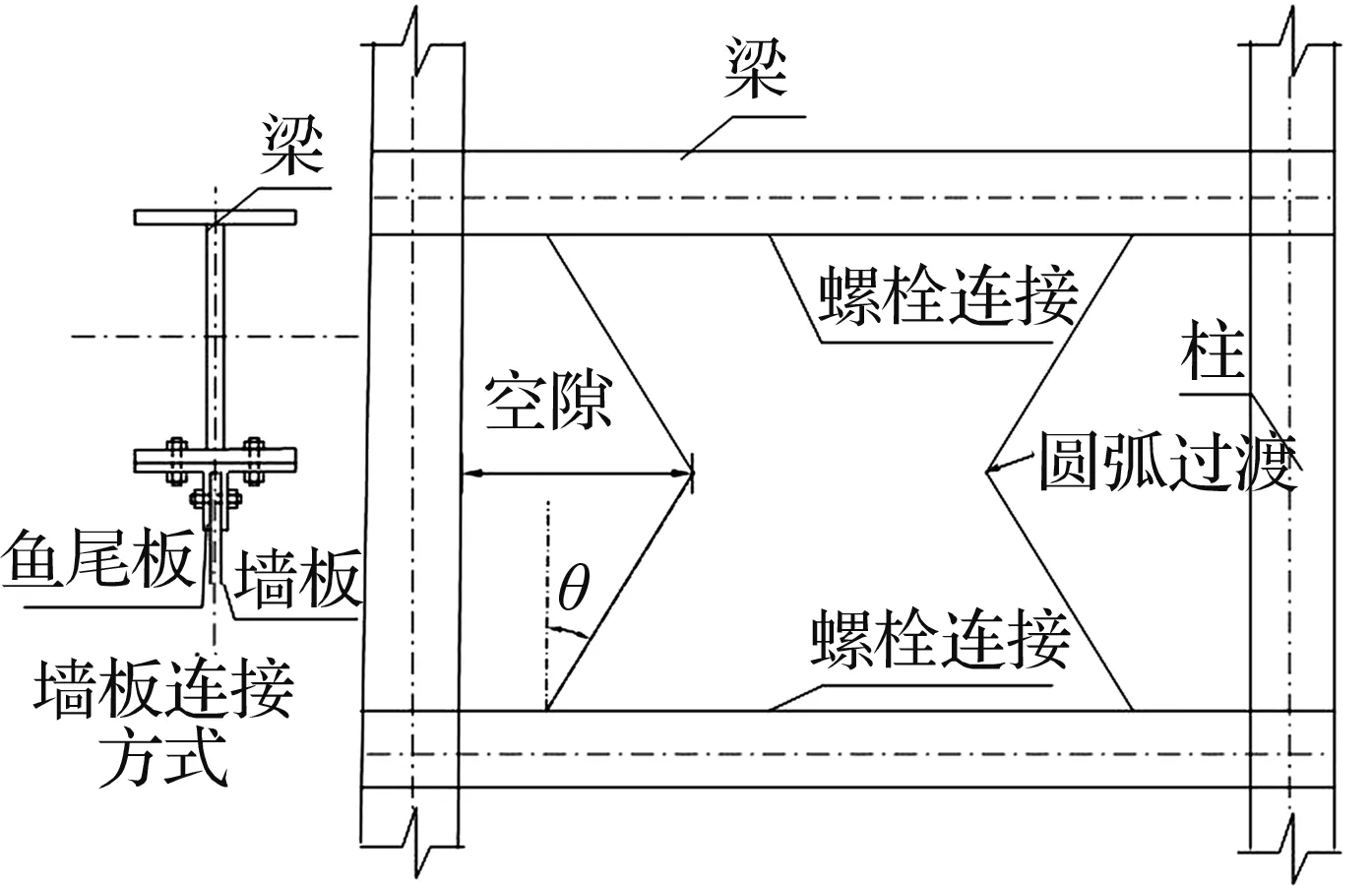
图1 X形钢板剪力墙示意图Fig.1 Schematic diagram of X shape steel plate shear wall
1 X形钢板剪力墙
X形钢板剪力墙模型如图1所示,由两边连接矩形板削弱腰部三角形区域而成,腰部的削弱处采用圆弧过渡,以减少应力集中,为了使墙板在自复位结构中替换方便,墙板与梁通过鱼尾板栓接。X形板由于削弱了腰部区域,节省了材料,减轻墙板自重,并为墙板穿孔提供了便利。除此以外,由于其两侧没有加劲,竖向不承担荷载,施工时可立即安装,避免了传统四边连接墙板需要待框架结构施工完毕后再安装墙板的缺点,减少了工期。
2 弹性抗侧刚度与水平承载力公式
2.1 几何模型
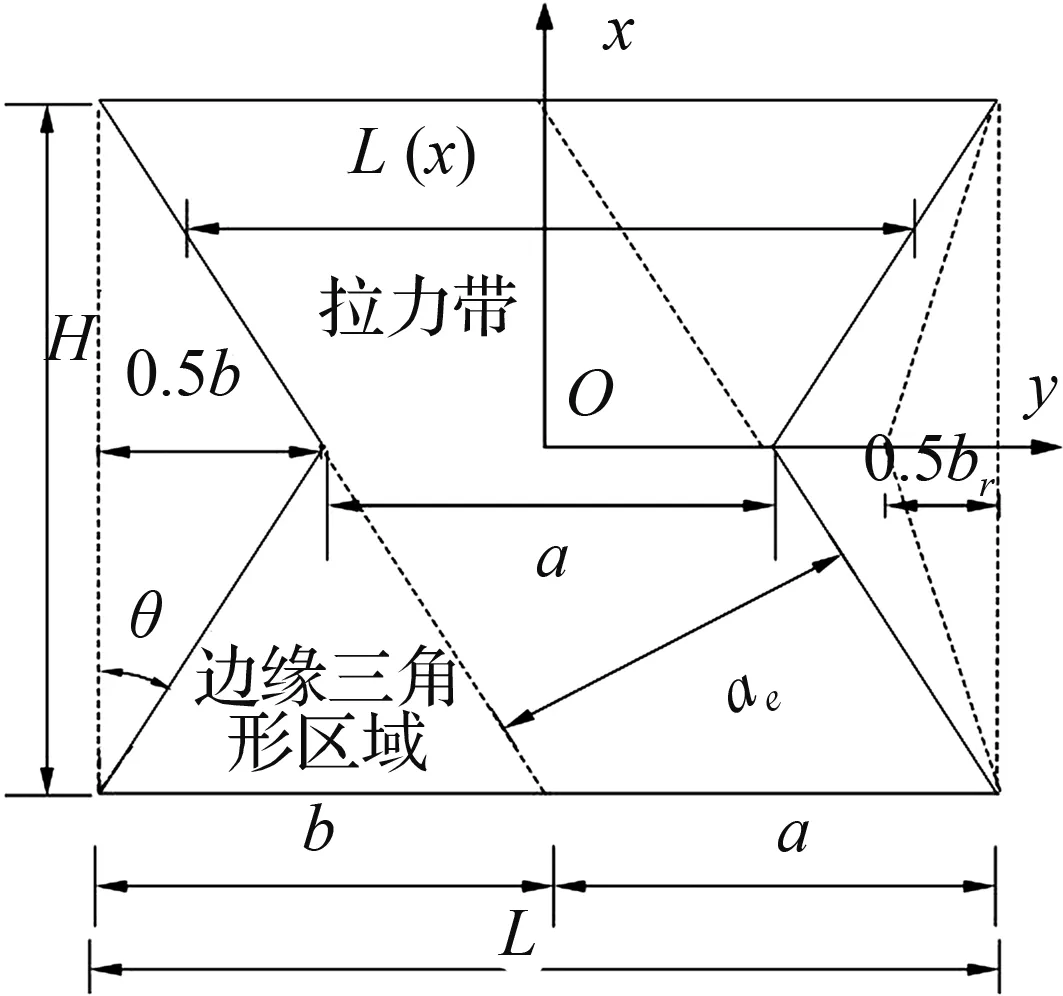
图2 几何模型Fig.2 Geometric model
X形钢板剪力墙简化模型如图2所示,L为其宽度,H为高度,a为拉力带宽度,b为墙板宽度减去拉力带宽度,br为削弱宽度,ae为拉力带有效宽度。考虑到实际工程,本文研究跨高比L/H范围从0.5至2.5。
X板和两边连接矩形板一样,其水平受剪承载力主要由拉力带提供,为了不破坏拉力带从而降低承载力,应使腰部宽度大于等于拉力带宽度a;在不显著降低承载力的同时,还应考虑尽量减少对拉力带的约束,使其在自复位结构更易实现复位。基于以上两点,取br=b,即墙板腰部宽度等于拉力带宽度。根据Thorborn(THORBURN L J, KULAK G L, MONTGOMERY C J.Analysis of steel plate shear walls[J]. Structural.Engineering Rep.No.107.Edmonton:University of Alberta, Canada, 1983)的推导,拉力带倾斜角θ与跨高比有关:
(1)
根据图1,可以求得b与L的几何关系:
(2)
式中,z为腰宽削弱比例,仅与跨高比有关。根据式(2),在X形剪力墙中,由跨高比控制削弱宽度。
2.2 弹性抗侧刚度及承载力公式

图3 荷载—位移曲线Fig.3 Load-drift curve
如图3所示,X型板的抗侧刚度分为屈曲前和屈曲后两个阶段,第一阶段,墙板尚未屈曲,墙板整体提供抗侧刚度;第二阶段,墙板失稳之后,墙板主要依靠拉力带提供抗侧刚度,边缘的三角形区域不再贡献刚度,此时刚度发生突变。由于两者受力机理不同,需要分别考虑这两个阶段的抗侧刚度。为简化分析,在推导墙板抗侧刚度时候做出如下假设:
① 当墙板处于屈曲前阶段时,平面外变形很小,在受弯矩影响时,仍然满足平截面假定。
② 梁与墙板可以认为墙板刚接于梁,由于一般梁上下均有墙板,此时拉力带相互抵消,可认为梁刚度无穷大。
③ 墙板屈曲后,不考虑拉力带以外部分对刚度的贡献。
推导水平承载力公式时,主要考虑以下两点:
① X形墙板没承载力主要由拉力带提供,且不考虑拉力带外墙板的贡献。
② 假设钢材为理想弹塑性材料,不考虑材料硬化的影响。
2.2.1 X形钢板剪力墙初始抗侧刚度
当墙板屈曲前,由板整体提供抗侧刚度,此时可认为墙板是楔形深梁,因此需要分别考虑剪切变形和弯曲变形对刚度的贡献。X形钢板剪力墙简化力学模型如图4所示,弯曲刚度和剪切刚度可视为两个串联弹簧共同作用,其抗侧刚度可以表达为:
(3)
其中δt为总柔度,即在单位力下墙板总侧移,δm为单位力下,由弯曲变形产生的侧移,δs为单位力下,剪切变形产生的侧移,Ks和Km分别为剪切刚度和抗弯刚度。参考谭平[13]对开菱形孔钢板剪力墙的推导,δm可以表达为:
(4)
式中E为钢材弹性模量、L为墙板跨度、H为墙板高度、t为板厚、km为弯曲折减系数,仅与跨高比有关:
(5)
从(4)知,当板厚度和弹性模量确定时,δm取决于跨高比。

(a) 受力简图(b) V图(c) 剪切变形图(d) M图(e) 弯曲变形图(f) 中联弹簧
由于板跨高较大,剪切变形的影响不可忽略,参考文献[11],并经过推导可得:
(6)
式中剪切折减系数km,与跨高比有关:
(7)
由图5可知,km和ks由跨高比控制,当跨高比无穷大时,两者接近1,此时X形板的抗侧刚度与矩形板一样。
根据式(3)可得X板初始抗侧刚度为:
(8)
结合式(4)和(6),初始弹性抗侧刚度仅与墙板厚度t、弹性模量E、跨高比H/L、弯曲折减系数系数km、剪切折减系数ks有关,其中km、ks可以用跨高比表示,故初始刚度可以表达为跨高比的函数:
(9)
如图6所示,f(L/H)与跨高比近似成线性关系,通过拟合,初始抗侧刚度可以表达为:
Kt=Et[-0.1+0.3(L/H)]。
(10)
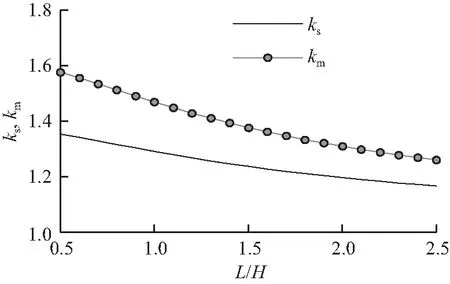
图5km,ks曲线
Fig.5kmandkscurves
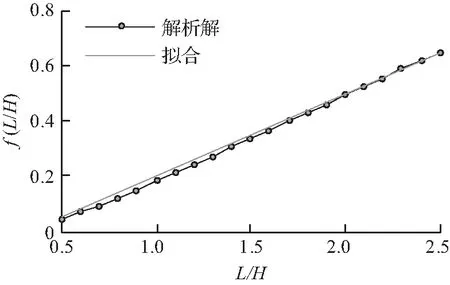
图6f(L/H)曲线
Fig.6f(L/H)curve
2.2.2 X形钢板剪力墙屈曲后抗侧刚度
墙板在屈曲后产生面外变形,图7(a)为高厚比600,跨高比为1的X形墙板在0.5 %位移角时面外变形图,由图可知,拉力带边缘和中部黑线处的平面外位移几乎零。根据图7(b)的受力分析,X板失稳可类比于图7(c)的杆系结构。杆模型中,压杆a、b受到拉杆c、d、e平面内的约束。当拉力T较小时,杆d的抗侧刚度较弱,不能有效约束杆a、b平面外位移,先发生侧移失稳,如图(d)所示;随着拉力增大,杆c、d、e的刚度增加,当超过门栏刚度时,压杆a、b由侧移失稳转化为无侧移失稳,此时杆的屈曲波形增加为两个,框架仍然具有一定抗侧刚度。对比图7(a)可知,墙板失稳与杆模型无侧移失稳类似,因此墙板在失稳后,仍然能继续提供额外的刚度。
根据Thorborn[9]的推导,拉力带提供的刚度Kp为表达为:
(11)
由于X形钢板剪力墙的倾斜角与跨高比有关,代入(1)式之后得出:
(12)
从式(12)中可知,当板厚为定值时,屈曲后刚度取决于跨高比,因此可以通过调节跨高比和板厚得到任意刚度。
2.3 腰部削弱和屈曲对抗侧刚度的影响
由于墙板腰部存在削弱,其初始弹性刚度相比两边连接矩形板有所降低,而屈曲的存在会进一步减少抗侧刚度,以下采用理论推导,给出了弹性状态下,墙板腰部削弱和屈曲对抗侧刚度的影响。
2.3.1 腰部削弱对抗侧刚度的影响
通过与两边矩形板初始刚度对比得出腰部削弱对刚度的影响,根据文献[14],两边连接矩形板抗侧刚度Kr由式(13)表达,对比式(8),二者区别在于两个折减系数km和ks。
(13)



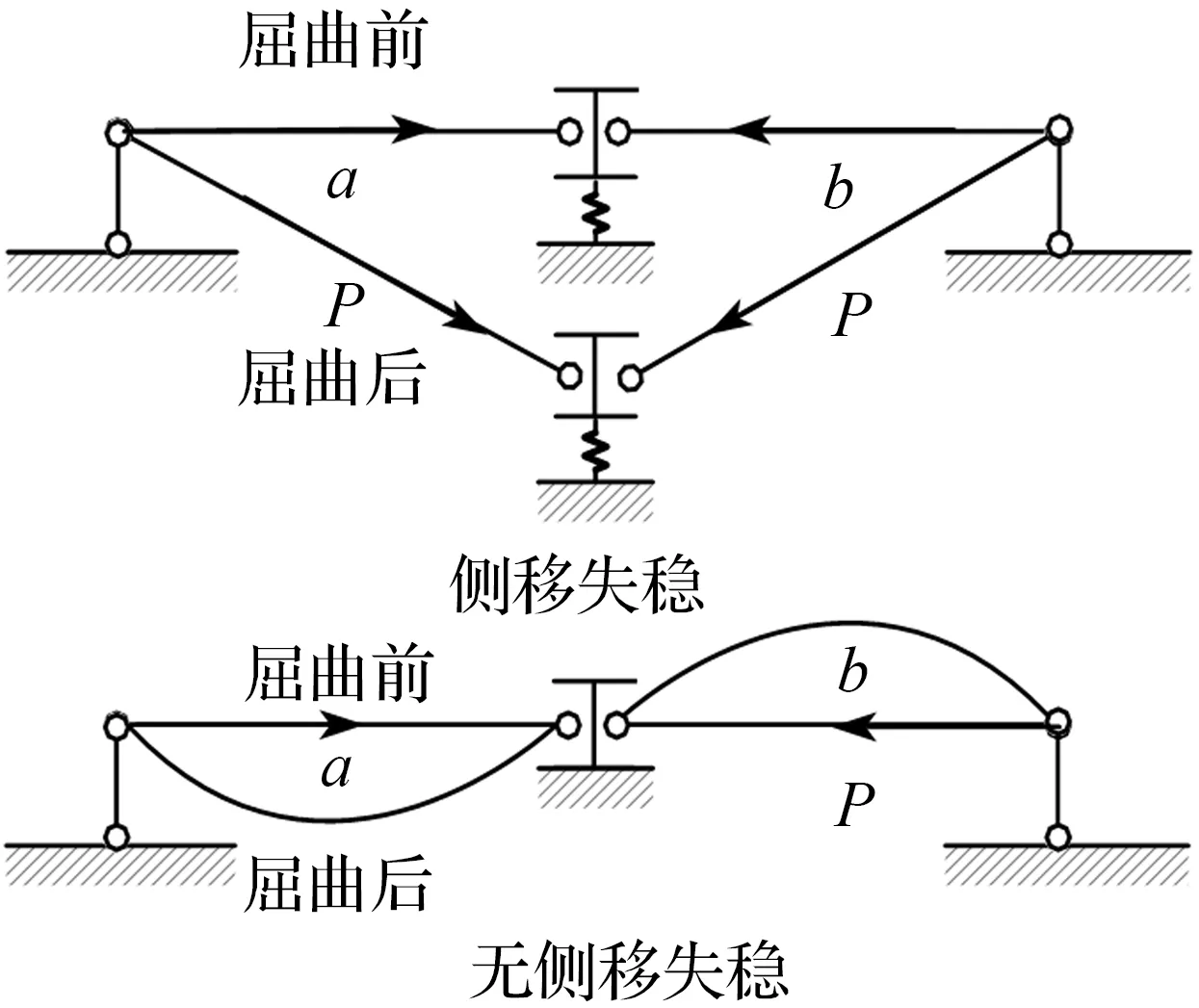
图7X形钢板剪力墙屈曲后简化力学模型
Fig.7Simplifiedmechanicalmodelofpost-buckledXshapesteelplateshearwall
如图8所示:①当跨高比较小时,腰部削弱对墙板初始刚度影响较大;②随着跨高比的增大,削弱幅度逐渐减少;③跨高比无穷大时,km,ks逐渐接近于1,即矩形板和X板两者抗侧刚度相等;④虽然X板比起矩形板刚度有削弱,但最大削弱仅为30 %左右。
2.3.2 屈曲对刚度的影响
墙板屈曲后刚度会产生突变,可以通过屈曲后刚度Kp与屈曲前刚度Kt的比值Kp/Kt衡量屈曲对刚度的影响:
(14)
如图9所示,当跨高比较小时,失稳后刚度削弱较大,最大削弱70 %,随着跨高比增加,削弱幅度减少,当跨高比无穷大时,Kp/Kt为0.78左右。由于形成拉力带之后,整体的受力转换为仅拉力带提供刚度,两个对角区域未提供刚度,因此刚度有一定削弱,而随着跨高比增加,对角区域所占整体面积越小,刚度削弱越少。综上,虽然屈曲后对墙板刚度产生了折减,但拉力带仍然提供了可观的刚度,特别对于薄板,在侧移角很小时就产生了失稳,刚度几乎全部由拉力带提供。

图8Kt/Kr曲线
Fig.8Kt/Krcurve
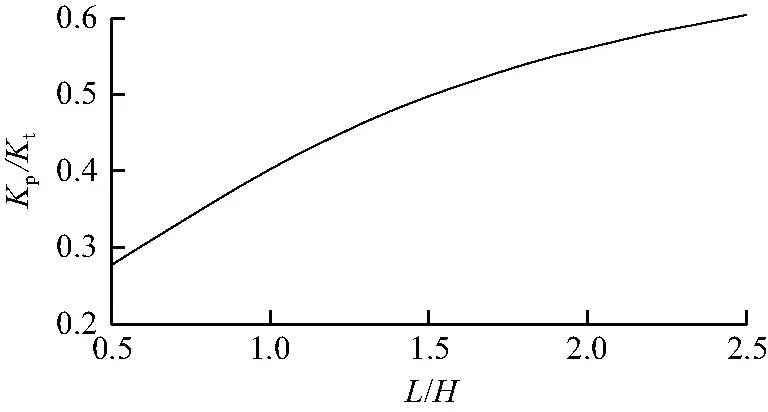
图9Kp/Kt曲线
Fig.9Kp/Ktcurve
2.4 水平承载力公式
X形钢板剪力墙主要依靠拉力带提供水平承载力,根据Sabelli[15]的研究,拉力带承载力可以由(15)表示:
(15)
式中a为拉力带宽度,fy为墙板屈服强度。由于倾斜角θ与跨高比有关,代入式(1)并化简,得到(16),在高度确定的情况下,承载力可由跨高比来控制。
(16)
可以根据(16)拟合出式(17)作为实际简化公式:
V=fytH[0.018+0.2255(L/H)-0.0394(L/H)2]。
(17)
由图10可知,随着跨高比增加,承载力增大。原因是当高度一定时,跨高比越大,钢板拉力带越宽,承载力随之增加。
3 有限元验证及分析
3.1 有限元模型
采用有限元软件ABAQSU6.14建立X形钢板剪力墙模型,模型简图如图11所示。试件尺寸高度统一为3.6m,跨高比分别为0.5、1、1.5、1.75、2,墙板厚度为2 mm、4 mm、6 mm和12 mm,其对应高厚比为1 800、900、600和300。腰部宽度统一取拉力带宽度a。
为了避免梁柱对墙板的影响,柱上端与梁节点铰接,柱下端约束U1,U2,U3,UZ1,UZ2,保证柱角能够绕UZ3方向转动。同时约束梁和柱U3方向,防止梁柱产生平面外位移。现有的研究表明,墙板的残余应力与鱼尾板对墙板的性能影响较小,为了简化分析,墙与梁采用绑定连接。墙板采用Q235级钢材,采用理想弹塑性本构,屈服强度为235 MPa,抗拉强度采用375 MPa,泊松比为0.3。采用von Mises屈服准则。为了考虑钢材受循坏荷载时,材料硬化的影响,模型中钢材采用随动强化。墙板采用四边形线性缩减单元(SR4)模拟。由于薄墙板极易发生面外失稳,屈曲后的几何非线性对模拟准确性影响极大,因此采用显式求解器。
墙板在生产与运输过程中,易产生面外变形,为了使模拟更加接近实际情况,对墙板施加初始缺陷,按照《钢结构工程施工及验收规范》(GB50205-2001)规定,墙板厚度小于14 mm时,取钢板跨度1/1 000,本文研究钢板厚度均小于14 mm,故统一取跨度的1/1 000。由于钢板剪力墙几何对称性,一阶和二阶模态一样,故施加前两阶初始缺陷。
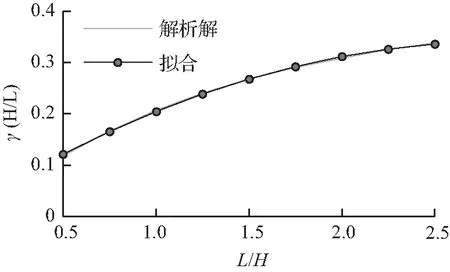
图10γ曲线
Fig.10γcurve
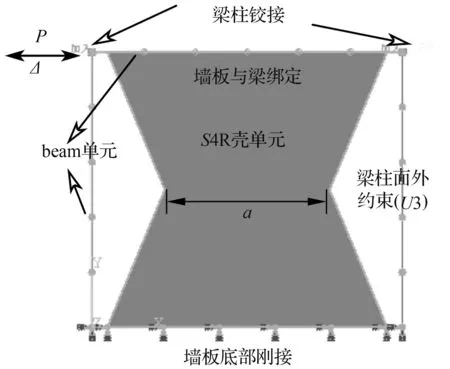
图11有限元分析模型
Fig.11Finiteelementanalysismodels
3.2 理论公式验证
3.2.1 弹性抗侧刚度验证
通过数值模拟,图12给出了理论推导初始抗侧刚度和有限元模拟结果。从图中可知,初始弹性抗侧刚度精度较高,且公式值均偏小,偏于保守。屈曲后抗侧刚度在跨高比小于1时,误差增大,这是由于在于推导公式时,未考虑拉力带外的三角形区域贡献。
图13给出了墙板屈曲后抗侧刚度,如图所示,跨高比较小时,理论值偏小,主要原因在于跨高比较小时,拉力带以外面积较大,此时这部分区域仍然提供了可观的刚度。当跨高比大于1.5时,拉力带起决定性因素,此时理论值与模拟值两者基本吻合。
综合模拟结果,当板高厚比大于300时,由于板较薄,在位移角很小的情况下就出现了屈曲,此时采用屈曲后刚度;当板高厚比小于等于300时,板较厚,初始抗侧刚度在弹性阶段影响明显,此事应该分别考虑屈曲前刚度和屈曲后刚度。
3.2.2 X形钢板剪力墙水平承载力验证
如图14所示,承载力简化公式(17)与模拟结果吻合,简化公式承载力全部偏小,较为安全。随着跨高比增加,公式误差越小,这是因为随着跨高比越大,其拉力带面积越大,此时承载力主要由拉力带提供,误差减小。

图12墙板初始刚度
Fig.12Initialstiffnessofshearwall

图13墙板屈曲后刚度
Fig.13Post-buckledstiffnessofshearwall
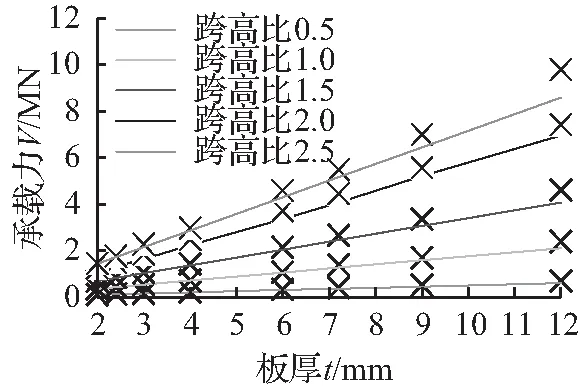
图14承载力
Fig.14Loadcarryingcapacity
4 参数分析
根据文献[8],自复位结构的滞回曲线可以看成自复位空框架与耗能器两者的线性叠加,为了简化分析,单独研究X形墙板的受力性能。由于X形钢板剪力墙的几何尺寸主要由高厚比λ、削弱宽度比br/b、跨高比β三者控制,选取此三者作为主要参数,研究不同情况下,X形钢板剪力墙的承载力、单推曲线、滞回性能以及耗能能力。
4.1 单调加载荷载—位移曲线
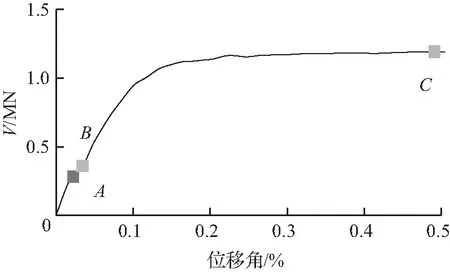
图15 X形钢板剪力墙荷载—位移角曲线Fig.15 Load-drift ratio curves of X shape steel plate shear wall
图15、16分别给出了跨高比为1,高厚比为600的X形钢板剪力墙在不同位移角下的的荷载—位移曲线和应力云图,综合图15、16可知:当墙板在位移非常小时(位移角0.04 %,图15中A点),墙板的应力云图对称,均匀受力,此时墙板的抗侧刚度可以按照式(10)求得;当层间位移角继续加大到0.05 %时,墙板发生屈曲,面外出现变形,墙板从整体受力过渡到形成拉力带(图15中B点),刚度产生突变,此时墙板刚度可按式(13)求得;随着位移角继续加大,墙板拉力带逐渐进入塑性,当位移角为0.5 %时,由图16(c)可知,拉力带大部分进入塑性,墙板提供稳定耗能;位移角增加到3 %时,拉力带继续增长,且全部进入塑性,拉力带外部三角形区域受力增加。

(a) 0.04 %位移角
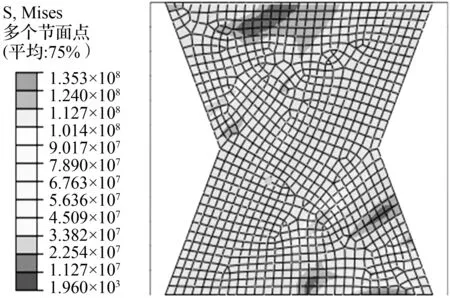
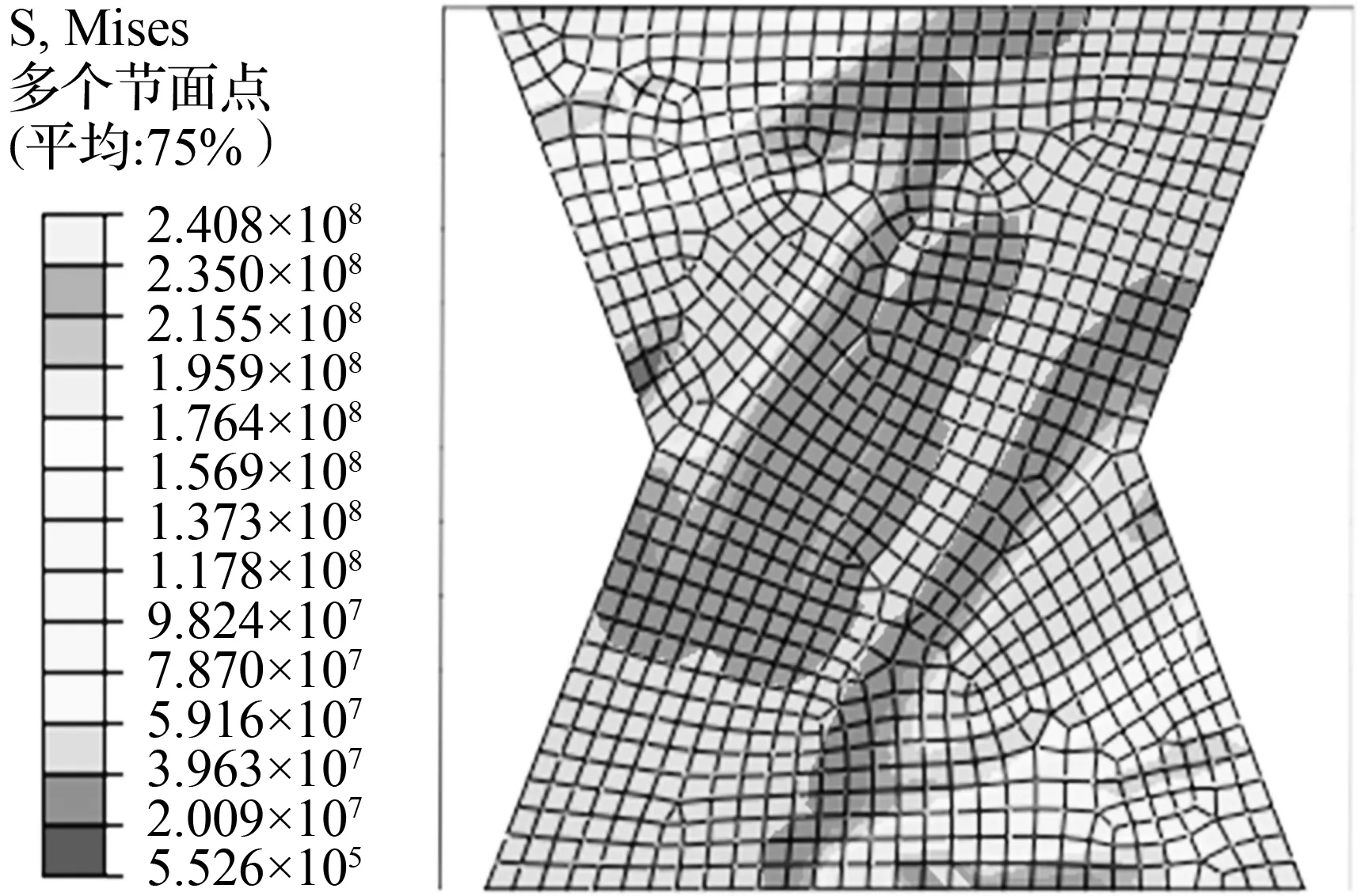
(c) 0.5 %位移角
图16X形钢板剪力墙应力云图
Fig.16Stressdistributionsofthespecimenatdifferentdrifts
图17(a)给出了在跨高比为1,高厚比λ不同情况下,X形墙板的荷载—位移曲线,图中曲线平滑,在4 %位移角时,承载力未下降,且随着高厚比减小,板越厚,其承载力越高。图17(b)给出了高厚比为600,跨高比分别为1和1.75的单调荷载位移角曲线,分析可知,在高厚比一定情况下,随着跨高比的增加,拉力带宽度增加,承载力显著提升。图17(c)给出了高厚比为600,跨高比为1矩形板和X板的荷载位移曲线图,从图中可以看出,相比于矩形板,X板更早进入塑性耗能,两者刚度、承载力相差不大,承载力未出现突降,延性较好。综合图17(a)、(b)、(c)可知X形剪力墙具有良好延性,这是因为承载力主要由拉力带承担,能够充分发挥钢材受拉性能好的优势。
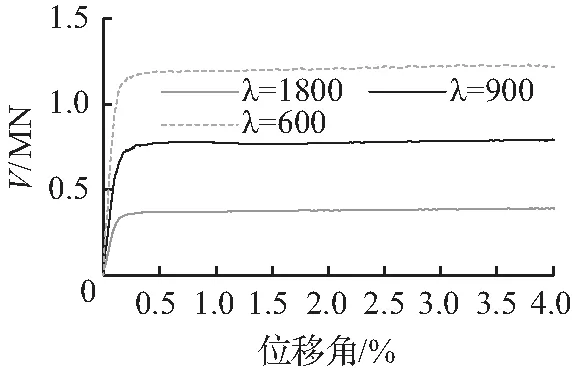
(a) 不同高厚比(b) 不同跨高比的X板 (c) X板和矩形板
4.2 与两边连接矩形板承载力对比
为了研究墙板不同的削弱宽度br对承载力的影响,取高厚比为600,跨高比为1,高为3 600 mm的X形钢板剪力墙作为为Base试件,同时增加三组对比试件,增加的试件底部宽度、厚度及高度与Base试件一致,其中第一组为矩形钢板剪力墙,其余两组试件的腰部削弱宽度br分别为X板的腰部削弱宽度b的0.5和1.5倍。各组尺寸如下表所示。

表1 不同参数板的承载力Tab.1 load carrying capacity with different parameters
根据表1结果,当br/b为0.5时,对矩形板削弱很小,承载力几乎相等,X形板承载力为矩形板的90 %以上,这是因为X板腰部虽然被削弱,但由于矩形板和X板最后均为拉力带提供承载力,所以削弱幅度并不大。当br/b为1.5时,削弱了拉力带有效宽度ae,承载力下降了近30 %。根据图14和表1结果,当br/b小于1时,墙板的水平承载力可以统一用式(17)。
4.3 往复加载滞回曲线
4.3.1 X板滞回曲线
可以通过滞回曲线衡量自复位结构中墙板的复位性能,滞回曲线在第二四象限越捏缩,则自复位结构复位效果越好。
图17中(a)(d)为跨高比为1的X形钢板剪力墙和矩形钢板剪力墙,在高厚比分别为300和1 800的滞回曲线,从图中可知,两边连接矩形板与X板在一三象限基本一致,承载力大致相当,但在二四象限,X板则呈现明显捏缩。图17(b)、17(e)为跨高比均为1,削弱宽度分别为b和1.5b的X形钢板剪力墙,如图所示,两者滞回曲线的二四象限大体一致,但削弱宽度为1.5b的墙板承载力却急剧下降,降幅达到30 %左右。通过削弱拉力带内部的墙板虽然更加容易实现在自复位结构中复位,但是却以承载力和耗能为代价。取高厚比相同,跨高比分别为1.5和1的X形墙板,滞回结果如图18(d)、(f)所示,不同跨高比情况下,滞回曲线均呈现捏缩,但随着跨高比增加,滞回环二四象限面积增大,这是由于当跨高比增加时,拉力带的约束逐渐增加,需要更大的力才能使拉力带倾斜角转换;高厚比为1 800时,跨高比对捏缩的影响较小,而高厚比为300时,跨高比对捏缩影响明显,可能原因是当板变厚时,除了腰部三角形区域对拉力带的约束外,厚板对平面外的约束比薄板更强,在拉力带转换倾斜角时需要更大的力。
综上:①无论高宽比和高厚比,X板滞回曲线均较为捏缩。②相比于矩形板,X板滞回曲线在捏缩的同时,承载力并未下降,因此更加适合于自复位结构。③当腰部的开口削弱到拉力带内部时,墙板滞回曲线虽然捏缩,但承载力会大幅度下降,故削弱宽度以到拉力带边缘为宜。

(a) 高厚比为300(b) 高厚比为300(c) 高厚比300

(d) 高厚比为1 800(e) 高厚比为1 800(f) 高厚比1 800

Fig.19 简化滞回曲线Fig.19 Simplified hysteretic loops
4.3.2 X板与矩形板滞回曲线捏缩对比
根据图18,X板和矩形板的滞回曲线可简化成图19,观察图19可知:墙板尺寸确定时,其水平承载力V可通过(17)得到;当墙板卸载时,X板和矩形板会发生失稳,此时的承载力Vp在过度段较为稳定,因此可以通过承载力V与卸载时力Vp的比值来衡量滞回曲线的捏缩程度。Vp/V越小,曲线越捏缩,越适用于自复位结构。为此设计了144个X板和矩形板模型,其高度统一取3 600 mm,跨高比分别为0.5、0.75、1、1.25、1.5、1.75、2、2.25、2.5,板厚取2 mm、2.4 mm、3 mm、4 mm、6 mm、7.2 mm、9 mm、12 mm,对应高厚比为1 800、1 500、1 200、900、600、500、400、300。通过数值模拟,分别求出其Vp/V值。如果如图20所示。
分析图20可知:①矩形板和X板的高厚比越大,即板越薄,其滞回曲线越捏缩。②当跨高比小于1.5时,跨高比越小,矩形板和X板滞回曲线越捏缩,跨高比大于1.5时,跨高比对滞回曲线捏缩程度的影响很小。③无论跨高比和高厚比,X形墙板的Vp/V均小于矩形板,同等情况下,X板比矩形墙板的滞回曲线更加捏缩。以跨高比为1.75,高厚比为600的X板为例,其Vp/V为0.24,而同等跨高比和高厚比的矩形板,其Vp/V为0.315,由此,在保证自复位结构复位的情况下,X墙板板厚可以比矩形板放大1.5倍左右,从而对自复位结构提供更多的刚度和承载力。综上X形墙板更加适用于自复位结构。
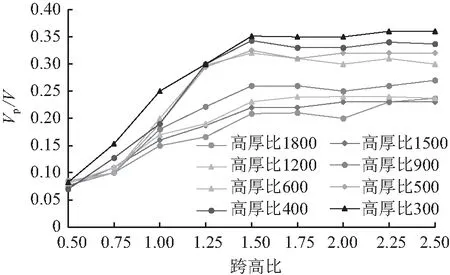
(a) 矩形钢板剪力墙

图20Vp/V曲线
Fig.20Vp/Vcurve
4.4 耗能能力
X形墙板在自复位结构中,不仅提供刚度和承载力,还需要有一定的耗能能力。可以通过等效粘滞阻尼比ζ合理地评估试件耗散能量的能力。为了研究不同参数对耗能能力的影响,图21给出了不同参数下等效阻尼比ζ随位移角变化曲线。
图21(a)为跨高比为1,高厚比不同的X形墙板的等效粘滞阻尼比,从图中可知,不同高厚比的X板耗能均较为稳定,四条曲线走向大体一致,等效阻尼比均在0.15以上。高厚比越小,等效阻尼系数ζ越大,当位移角大于2 %之后,虽然耗能能力出现一定退化,但退化幅度不大。图21(b)为高厚比均为600,不同跨高比的X墙板等效阻尼比曲线。从图中可知,跨高比越大,等效阻尼系数越大,耗能越稳定。图21(c)为跨高比为1,高厚比为600的墙板,采取不同削弱宽度墙板的等效粘滞阻尼比,如图所示,削弱宽度为0.5b时耗能最稳定,削弱宽度大于0.5b的墙板在位移角超过2 %之后均呈现退化。
综上,虽然X板滞回曲线较为捏缩,但其等效粘滞阻尼比均在0.15以上,在自复位结构中能够提供较为稳定的耗能能力。

(a) 不同高厚比(b) 不同跨高比(c) 不同削弱宽度
4.5 破坏模式
根据20个试件的模拟结果统计并结合理论计算,墙板的破坏模式主要是拉力带受拉压破坏。图22、图23给出了高厚比为600,跨高比为分别为1.5、1、0.5的X墙板破坏应力云图和主应力方向图。图中均形成明显拉力带,拉力带外部受力很小,当腰部削弱未触及拉力带边缘时,拉力带倾斜角与矩形板一致。

(a)


(c)

(a)
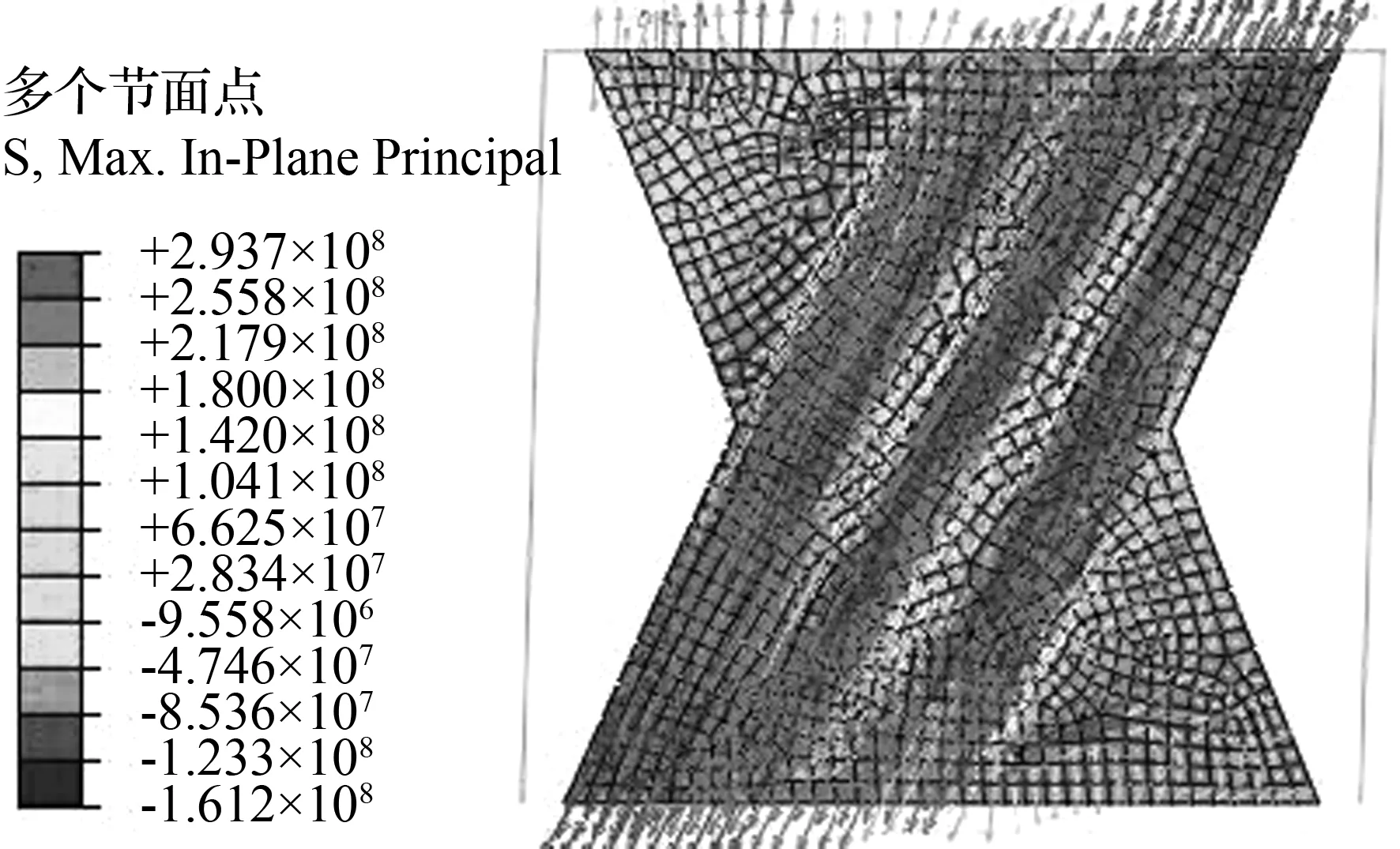

(c)
5 结论
① 提出了X形钢板剪力墙简化力学模型,推导了墙板的弹性抗侧刚度、屈曲后抗侧刚度、水平承载力公式。
② 对比矩形板,X形钢板剪力墙承载力和初始抗侧刚度均略有削弱,但均在75 %以上,说明本文提出削减形式具有可行性。
③ 屈曲对X形钢板剪力抗侧刚度削弱与跨高比有关,随着跨高比增大,屈曲对抗侧刚度的影响逐渐减弱。
④ X形墙板腰部削弱不能伸入拉力带内部,当腰部削弱到拉力带边缘时,对承载力影响不大。
⑤ 当墙板跨高比,板厚分别变大时,初始抗侧刚度,屈曲后抗侧刚度,水平承载力,等效阻尼比均随之增大。
⑥相比于两边连接钢板剪力墙,X形钢板剪力墙滞回曲线更加捏缩,适合于自复位结构。
⑦ X形钢板剪力墙板耗能较稳定,等效阻尼比均在0.15以上,能够为自复位结构提供稳定耗能。
⑧ 墙板板主要以拉力带受拉破坏为主,延性较好。

