基于板底脱空压浆处治前后力学行为对比分析

，，，

(1.西安建筑科技大学土木工程学院， 陕西西安710055;2.中铁一局集团勘察设计分公司, 陕西西安710054)

0 引言

水泥混凝土路面在服役期间，受车辆荷载和温度荷载的耦合作用，板底基层将产生累积塑性变形，致使路面板底与基层之间不再连续接触，形成板底脱空[1]，另一方面，脱空处随着雨水的侵入，其间的积水与基层材料中的细料形成泥浆，产生唧浆病害，加重板底的损伤程度[2]。板底压浆作为路面板底脱空处治的一种方法，由于其成本低，旧路面利用率高，技术成熟，工艺简便，且交通封闭时间短，因此已在工程中得到广泛应用[3]。

近年来国外在路面板底脱空方面的研究成果较少[4-6]，相比而言国内关于路面板底脱空方面研究较多，麻丽妹[7]引入自膨胀补偿收缩理论对压浆材料进行改良，推荐无机自补偿压浆材料适宜配合比，提出压浆材料冲刷系数指标；童申家[8]讨论了两种压浆材料脆性发展的规律，从长龄期使用性能考虑，建议选用有机压浆材料来减弱材料后期的脆性发展。我国采用的压浆材料主要为水泥粉煤灰类浆体，材料相对单一，且该材料可因硬化产生体积收缩等弱化行为，致使被压浆材料填满的路面板底脱空区域发生再次脱空[9]，处治效果并不理想。因此，压浆后的路面板力学效应亟待研究。

鉴于此，本文分别建立了板底脱空及压浆处治的有限元模型，探究脱空状态及压浆状态不同尺寸、厚度、材料模量的工况下，路面板弯沉及弯拉应力两大指标的变化趋势，总结其发展规律，为压浆材料性能弱化研究确立技术依据，促进研究发展与方便实际应用。

1 有限元计算模型

1.1 参数设置

模型中路面结构层的材料参数依据现行《公路水泥混凝土路面设计规范》(JTG D40-2011)取值，采用弹性地基上有限尺寸薄板建立有限元计算模型[10]，演化混凝土路面板底脱空及压浆处治。将水泥路面简化为面层、脱空层、基层及土基，结构采用solid185单元模拟。土基取7 000 mm×6 000 mm×6 000 mm，基层取7 000 mm×6 000 mm×190 mm，面层取5 000 mm×4 000 mm×300 mm，脱空部分和压浆部分为半径1 000 mm、高10 mm的1/4圆柱体。路面各层的材料参数如表1所示。路面结构计算模型如图1所示，有限元分析模型如图2所示。

表1 路面结构及材料参数表Tab.1 Pavement structure and material parameters table

图1路面结构计算模型(单位：mm)
Fig.1Pavementstructurecalculationmodel(Unit:mm)

图2有限元分析模型
Fig.2Finiteelementanalysismodel

1.2 荷载施加

我国现行《规范》[11]中规定标准轴载的轮载P=100/4(kN)，轮胎接地压强为0.7 MPa。本文选用单轴—双轮载作为计算荷载，为了满足计算精度以及考虑方便单元划分，将椭圆形轮载简化为单轮长宽均为200 mm的双轮矩形轮载，轮间的距离为300 mm，双轮组中心的间距为1 800 mm，轮载图示见图3，由于本文采用的是板角脱空模型，因此考虑最不利情况，施加荷载的初始位置位于脱空正上方，荷载作用位置见图4。

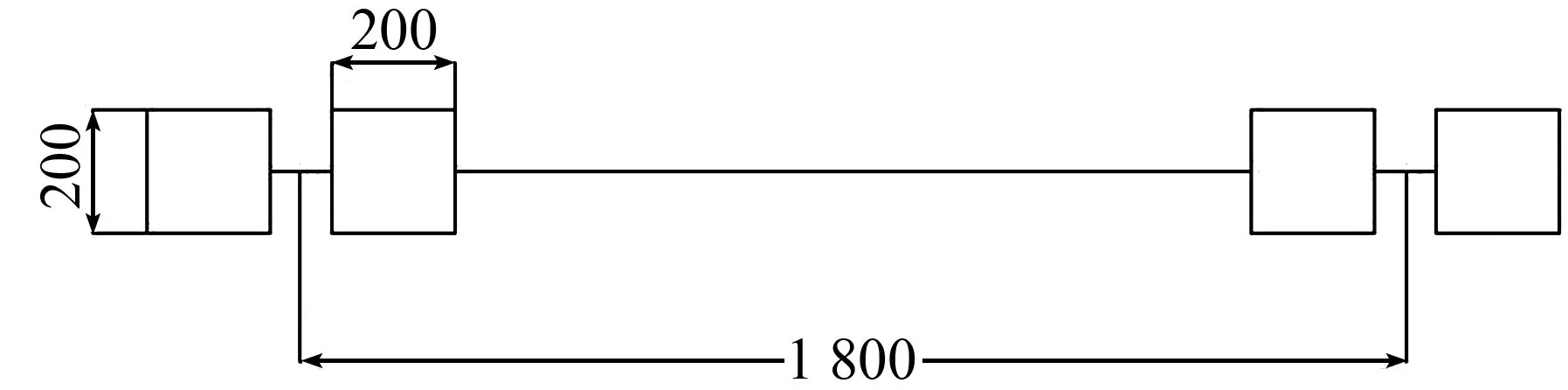
图3单轴—双轮组图示(单位：mm)
Fig.3Singleshaft-doublewheelgroupdiagram(Unit:mm)

图4图4荷载作用位置图(单位：mm)
Fig.4Loadlocationmap(Unit:mm)

2 脱空及压浆处治形式对水泥板板角弯沉和受力影响

2.1 板底脱空尺寸及处治尺寸对水泥板板角弯沉及受力影响

为对比分析压浆处治前后脱空尺寸及处治尺寸对水泥板板角弯沉和受力影响，路面板底脱空尺寸及压浆处治尺寸分别选取为200 mm、400 mm、600 mm、800 mm和1 000 mm，其他参数保持不变。其计算结果如表2、表3所示，其计算结果折线图如图5、图6。

表2 脱空尺寸对路面板板角应力及弯沉影响计算结果Tab.2 Void size of the road slab angle stress and deflection calculations

表3 处治尺寸对路面板板角应力及弯沉影响计算结果Tab.3 Treatment size of the road slab angle stress and deflection calculations

图5不同脱空及处治尺寸下路面板弯沉折线图
Fig.5Differentvoidandtreatmentsizeundertheroadplatebendcurve

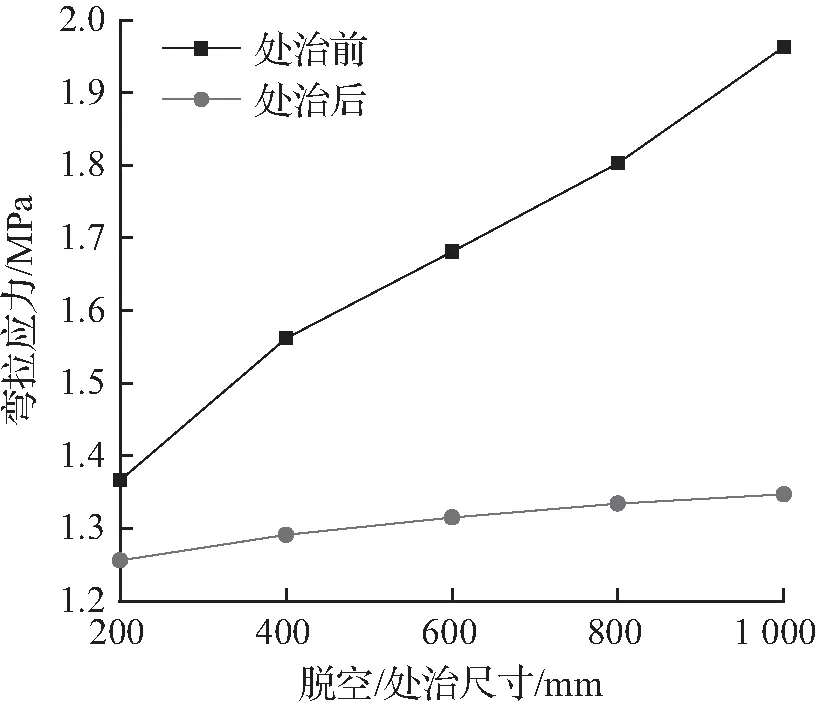
图6不同脱空及处治尺寸下路面板弯拉应力折线图
Fig.6Differentvoidandtreatmentsizeundertheroadbendingbendingstresslinechart

由表2、表3，图5、图6可以得出：

① 板底脱空路面的弯沉随着脱空尺寸的增大而逐渐增大，总体增幅达到37.30 %；当脱空尺寸由200 mm增大到400 mm时，弯沉增长速率最大，达到2.32 %；而当脱空尺寸由400 mm逐渐扩大到800 mm时，对应弯沉增长速率减缓；当从800 mm演化到1 000 mm时，弯沉上升趋势较大。根据其演化特点，可以提出在本模拟条件下脱空演化三阶段：当脱空尺寸为200～400 mm时为突变阶段，400～800 mm时为发展阶段，800～1 000 mm时为加速扩展阶段。而对比板底压浆处治之后可以发现，压浆后随着处治尺寸的不同，板底弯沉均明显下降，降幅可达7.76 %以上。特别地，当压浆尺寸为1 000 mm时，对应弯沉下降率达到28.47 %，说明此时压浆处治效果较好。

② 板底脱空路面的弯拉应力随着脱空尺寸的增大，呈整体增大的趋势。当脱空尺寸由200 mm演化至400 mm时，弯拉应力出现突变，增长率达到14.35 %，而脱空尺寸在400～1 000 mm范围内时，弯拉应力增长较缓慢。而对比压浆后板底弯拉应力可以发现，压浆后板底弯拉应力下降明显。尤其当压浆尺寸为1 000 mm时，对应弯拉应力降幅达到31.38 %，压浆处治效果明显；当压浆尺寸由200 mm演化到400 mm时，弯拉应力增长速率达到2.71 %，说明在此过程中，压浆尺寸的影响较大。

2.2 板底脱空深度及处治厚度对水泥板板角弯沉及受力影响

为对比分析压浆处治前后脱空深度及处治厚度对水泥板板角弯沉和受力影响，路面板底脱空深度及压浆处治厚度分别选取为5 mm、10 mm、15 mm、20 mm和25 mm，其他参数保持不变。其计算结果如表4、表5所示，其计算结果折线图如图7、图8。

表4 脱空深度对路面板板角应力及弯沉影响计算结果Tab.4 Void depth of the road slab angle stress and deflection calculations

表5 处治厚度对路面板板角应力及弯沉影响计算结果Tab.5 Treatment thickness of the road slab angle stress and deflection calculations

图7不同脱空深度及处治厚度下路面板弯沉折线图
Fig.7Curvediagramofthedeflectionofthepavementslabwithdifferentvoiddepthstressofpavement

图8不同脱空深度及处治厚度下路面板弯拉应力折线图
Fig.8Curvediagramofbendingandbendingunderdifferentvoiddepthandthicknessandtreatmentthickness

由表4、表5，图7、图8可以得出：

① 当板底脱空深度在5～10 mm时，板底弯沉产生突变，这是由于水泥板突然失去基层约束而导致的。而随着脱空深度的继续增长，板底弯沉和弯拉应力基本趋于平稳状态，在不考虑板底脱空受力后空隙闭合而形成二次支撑即脱空区域不变化的情况下，相应的弯沉和应力都应该变化不大，这与线弹性理论分析一致。

② 随着处治厚度的不同，板底的弯沉和弯拉应力均明显下降，且降幅分别可达到27.4 %和31.4 %以上。而对比处治尺寸下弯沉和弯拉应力变化趋势发现，当处治厚度为5～10 mm、处治尺寸超过800 mm时，处治厚度对路面板的影响程度大于处治尺寸；当处治厚度大于10 mm、处治尺寸为400～800 mm时，处治尺寸对路面板影响程度更高。

2.3 板底基层模量及压浆模量对水泥板板角弯沉及受力影响

参考相关文献，压浆模量选取100～1 000 MPa之间是合理的[2]。为了研究板底基层模量和压浆模量对水泥板板角弯沉及受力的影响，赋予基层模量分别为800 MPa、1 000 MPa、1 200 MPa、1 400 MPa、1 600 MPa进行研究，赋予压浆模量分别为100 MPa、200 MPa、500 MPa、800 MPa、1 000 MPa，其他参数保持不变。其计算结果如表6、表7所示，其计算结果折线图如图9、图10。

表6 基层模量对路面板板角应力及弯沉影响计算结果Tab.6 Basic modulus of the road slab angle stress and deflection calculations

表7 压浆模量对路面板板角应力及弯沉影响计算结果Tab.7 Grouting modulus of the road slab angle stress and deflection results

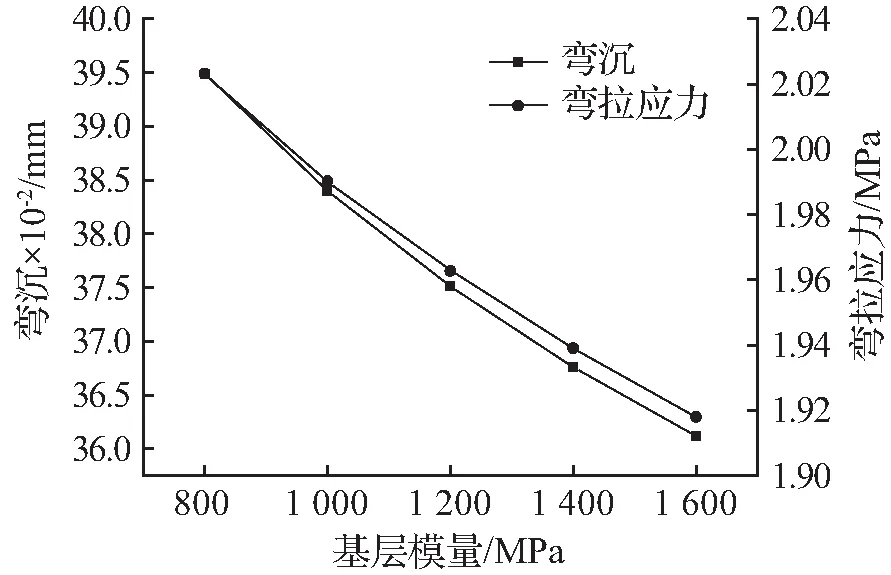
图9基层模量对路面板弯拉应力及弯沉折线图
Fig.9Baselayermodulusofthepavementbendingstressandbendinglinechart

图10压浆模量对路面板弯拉应力及弯沉折线图
Fig.10Groutingmodulusofpavementbendingstressandbendinglinechart

由表6、表7，图9、图10可以得出：

① 基于板底脱空和压浆尺寸1 000 mm、脱空和压浆处治厚度10 mm工况下，随着基层模量及压浆层模量的逐渐增加，对应水泥路面板的弯沉和弯拉应力均逐渐降低。尤其地，在压浆处治过程中，压浆模量在100～400 MPa范围内弯沉和弯拉应力下降速率较快，说明在此范围内弯沉及弯拉应力对压浆模量敏感性较高。

② 在基层模量等于800 MPa的条件下，当压浆模量等于基层模量时，弯沉与弯拉应力的下降率分别为31.48 %和33.1 %；当压浆模量小于基层模量时，弯沉与弯拉应力的下降率分别为30.2 %和32.2 %；当压浆模量大于基层模量时，弯沉与弯拉应力的下降率分别为32.1 %和33.4 %。综上可以认为，当压浆模量大于基层模量时，处治效果更好。

③ 当压浆材料模量大于基层材料模量时，随着压浆材料模量增加，路面板弯沉和弯拉应力下降趋势渐渐平缓，而压浆材料模量在大于1 200 MPa后，其处治效果将大幅降低，材料性能没有充分利用。综上认为，压浆材料模量的选择不宜与基层材料模量相差过大，且在0～200 MPa范围内是合适的。

3 结论

① 在本文建模和模拟条件下，根据板底脱空尺寸对路面板底的影响提出板底脱空演化三阶段：脱空尺寸在200～400 mm时为突变阶段，在400～800 mm时为发展阶段，在800～1 000 mm时为加速扩展阶段。压浆处治过程中应着重控制处治尺寸变化的影响，及时地处理能有效降低路面板开裂的趋势，从而预防路面病害的发生。

② 随着处治厚度不同，板底弯沉和弯拉应力降幅分别可达27.4 %和31.4 %以上，处治效果明显。当处治厚度较小时，其对路面板的影响较处治尺寸大；而当处治尺寸较小时，处治尺寸对路面板的影响更大。

③ 在压浆处治过程中，当压浆材料模量值大于基层材料模量值时，其处治效果较好。但压浆材料模量值不宜大于1 200 MPa，同时压浆材料模量的选择宜与基层材料模量相差在0～200 MPa范围内，否则压浆处治效果将大幅降低，材料性能将得不到充分利用。