一维和三维联合动力学仿真方法在活塞发动机曲柄连杆机构动力学分析中的应用*

蔺红鹏 杜发荣 徐 征 周 煜

（北京航空航天大学能源与动力工程学院 北京 100191）

引言

二冲程航空重油发动机作为目前最具发展潜力的小型活塞发动机之一，它继承了活塞式航空发动机体积小、重量轻、功率密度大等优点[1-2]，更适合机体空间有限的无人机[3-5]。航空重油是指馏分在航空煤油与柴油之间的航空油料[6]，与传统航空汽油相比，重油具有粘度高，挥发性差等特点，从而提高了燃料使用和储运的安全性，同时随着燃料一体化的发展趋势，重油的使用更有利于简化后勤保障，在军队和通用航空领域应用前景广阔[6-9]。

本研究中某型二冲程航空重油发动机，由于其将装备于固定翼飞机或直升机作为动力，因此为保证飞机的飞行安全，对航空发动机提出更为严苛的要求[10]，如从动力输出上，要有比地面动力更好的平顺性和平衡性[11-12]，否则由此产生的不平衡力及力矩将转变成翼载荷；同时要求发动机具有超高的可靠性，不能出现空中停车等重大事故[13]。曲柄连杆机构作为内燃机的核心，历来受到内燃机研究人员的重视[14]，因此对曲柄连杆机构的动力学分析非常必要。

目前国内外对曲柄连杆机构的动力学分析方法很多，且比较成熟和完善。曲柄连杆机构动力学分析方法有解析法、图解法和数值方法[15]。解析法精度高，但对复杂机构工作量大，且实现起来有困难；图解法形象直观，但精度不够，适用性较差。随着计算机技术的不断发展，用数值方法求解高度非线性的微分方程组成为了可能，使得复杂工程问题可得到更精确的解。前人在发动机动力学分析方面做了很多工作[16-21]，如张文灿[16]基于单缸机的一维动力学分析只基于一维模型进行，不能具体反映每个部件详细的应力分布及变形；三维的数值仿真对模型做出很多假设，忽略部件弹性变形，如吴楠[19]将部分或全部部件视为刚体，或将曲柄连杆机构每个部件分开单独进行弹性的有限元分析，虽然考虑了部件的弹性变形，但对于数值计算的边界条件和非线性因素忽略较多，不能真实反映部件的受力和部件间的相互作用，在模型分析的完整性和精确度上都有不同程度的局限性。

本文提出基于GT-POWER与ABAQUS结合的动力学分析方法，更全面地对模型进行覆盖360°全循环载荷分析，基于ABAQUS的三维分析采用运动弹性动力学方法，将所有部件视为弹性体，并考虑几何与接触等非线性因素，在基于GT-POWER的一维分析基础上，以一维分析结果作为载荷边界条件，对受载严重的冲程重点分析，可以减少计算点，更高效地得到更为精确的计算结果。分析中重点考虑基于二冲程和航空发动机的独特要求，填补针对二冲程重油航空发动机动力学分析研究的空白，对重油航空发动机相关结构设计具有重要意义。

1 基于GT-POWER的发动机曲柄连杆机构一维动力学分析

1.1 建立一维热力循环及动力学分析模型

GT-POWER涵盖了发动机的热力、机械、流体和结构等各个方面，内燃机的模型库丰富又完整，且计算速度快，功能强大。本文首先根据二冲程重油发动机的循环参数，应用GT-POWER建立发动机一维热力循环模型，并进行参数优化，建立一个符合性能要求的发动机热力循环模型如图1所示。本研究的对象为一台直列两缸的二冲程航空发动机，曲轴旋转360°CA完成一个循环，两缸发火顺序相位差180°CA。发动机的基本参数如表1所示。

表1 发动机技术规格表

在发动机热力循环模型的基础上建立GTPOWER的动力学分析模型。建模过程中一些参数需根据结构进行计算或实际情况确定，如曲柄臂转动惯量、曲柄销惯性矩以及轴承的径向容差和润滑油性能的选取等。建立的模型如图1所示，在两个模型联合仿真的基础上得到发动机整个循环内的动力学参数，并与理论计算结果作对比验证其正确性。

1.2 一维动力学计算结果

在动力分析中，不计自重和摩擦阻力，主要分析气压力、往复和旋转惯性力等在曲柄连杆机构中的作用情况，分析活塞侧压力的大小和规律，连杆轴颈以及曲轴主轴颈等运动副的载荷分布规律。计算结果如下：

1）发动机气缸内的工质压力是整个动力装置的原动力，气压力-曲轴转角曲线如图2所示。

图1 发动机GT-POWER一维仿真模型

图2 发动机气压力-曲轴转角曲线

2）曲柄连杆机构各部件运动中产生惯性力，活塞往复运动的惯性力是导致发动机不平衡的主要原因，曲轴定速旋转其旋转惯性力为定值302N，如图3所示。

3）发动机各运动副的载荷及其分布

图3 惯性力曲线

作用在活塞顶上的气压力和运动件惯性力的最终作用表现在各个运动副所受的载荷及其分布规律。如图4、图5所示，其中活塞销载荷与连杆小头载荷互为反作用力；曲柄销载荷与连杆瓦载荷互为反作用力。

图4 活塞销载荷分布

图5 连杆瓦载荷分布

2 基于装配体下的ABAQUS曲柄连杆机构动力学分析

2.1 运动弹性动力学理论与数学模型

弹性动力分析的任务是研究曲柄连杆机构在外部载荷和自身惯性力共同作用下的运动和受力情况。应用运动弹性动力学分析方法建立有限元模型，不仅考虑了系统的弹性变形，建立更精确的运动微分方程，而且具有有限元的运算模式统一，模型适应性广的特点。本研究应用基于“瞬时结构假定”的运动弹性动力学分析方法，即曲柄连杆机构在运动循环中某一位置，将机构的形状和作用于其上的负荷瞬时“冻结”，从而将机构利用结构的方法分析[22]。基本步骤是：

1）将曲柄连杆机构各构件划分单元，在各单元指定点设置结点；

2）选择位移模式，建立广义坐标，从拉格朗日方程导出单元的运动微分方程；

3）将单元运动方程集合为系统的运动方程，其一般形式如下：

式中：[M]为系统质量矩阵；[C]为系统阻尼矩阵；[K]为系统刚度矩阵；{F}为系统载荷矩阵；{x}为系统广义坐标列阵。

式（1）的实质是广义的牛顿第二定律，机械振动学已经给出了上式的解法。这个非齐次微分方程组的解包括两部分，一是外载荷为零的自由振动齐次解，由于振动能量耗散，振动很快消失；另一个是系统在外界激励下的稳态响应。将上式解耦：

式（2）中{ψN}为正则振型矩阵，也即形函数矩阵，代入系统运动微分方程，并左乘{ψN}T，化简后得：

方程解耦完成，令qNi=xqieiωt，代入上式：

式中：λi=ω/ωi，i=1，2，…，n。

求出系统运动微分方程可得到广义坐标x，进而根据几何方程、物理方程等求出曲柄连杆的应力应变及其真实的位移、速度、加速度以及零部件的变形等。

2.2 有限元模型的建立与边界条件

发动机曲柄连杆机构系统主要包括活塞、活塞销、连杆以及曲轴等，不同部件采用不同材料，具体如表2所示。由于活塞为非对称结构，为提高仿真精度，考虑曲轴润滑油道及曲柄销减重孔，因此采用全模型。结合发动机的基本参数和制造工艺，在CATIA中建立基于特征控制的发动机三维模型，在Hypermesh中进行结构离散。其中缸套和活塞销为六面体一阶单元C3D8R，其余部件采用C3D4四面体单元，使网格相对于模型具有较高的几何相符率。对预计应力较大区域进行网格加密，如活塞销孔内沿及支撑肋等。共生成664 028个单元，185 388个节点，如图6所示。

表2 曲柄连杆机构材料表

图6 曲柄连杆机构有限元模型

发动机循环的动力学分析采用基于“瞬时结构假定”的运动弹性动力学分析方法，每隔10°CA选取一个计算点，对不同计算点的模型采用不同的边界条件。

为消除模型刚体位移，曲轴主轴颈6个自由度全约束，保证结构稳定。载荷边界条件为两个活塞顶面承受来自燃烧室的气压力，可通过发动机热力循环软件GT-POWER仿真得到。考虑运动副存在间隙或接触的状态非线性，在气缸套和活塞裙部、连杆大头和曲柄销等接触面设置接触对，接触对主从面合理的选择不仅可以保证数值计算的顺利进行，还可减少接触搜寻算法的计算成本。

2.3 ABAQUS动力学分析结果

应用ABAQUS/Standard求解器通过运动弹性动力学方法求解，获得曲柄连杆机构变形及应力结果。由于在气缸达到最高爆发压力11 MPa时（上止点后5°CA）机构受载最恶劣，因此取上止点后5°CA、40°CA及75°CA对其应力应变、变形及载荷作分析。如图7所示。

从图7a看出曲轴转角为5°CA时机构受载最恶劣，部分应力超出了材料的许用值，但经过结构优化配合热处理工艺可消除危险截面。如连杆小头出现基于赫兹理论的边沿效应，应力达到1 006 MPa，本文对此结构优化后重新计算，应力值降为407.43 MPa，如图13所示，再配以热处理及喷丸等工艺可以进一步提高连杆小头承载能力。优化后的机构在最高爆发压力下应力最大且安全，随着曲轴转角的继续增大，应力也相应减小，如图18所示，因此在其它转角下机构都是安全的。

曲轴在上止点后5°CA、40°CA及75°CA的应力分布如图8所示。

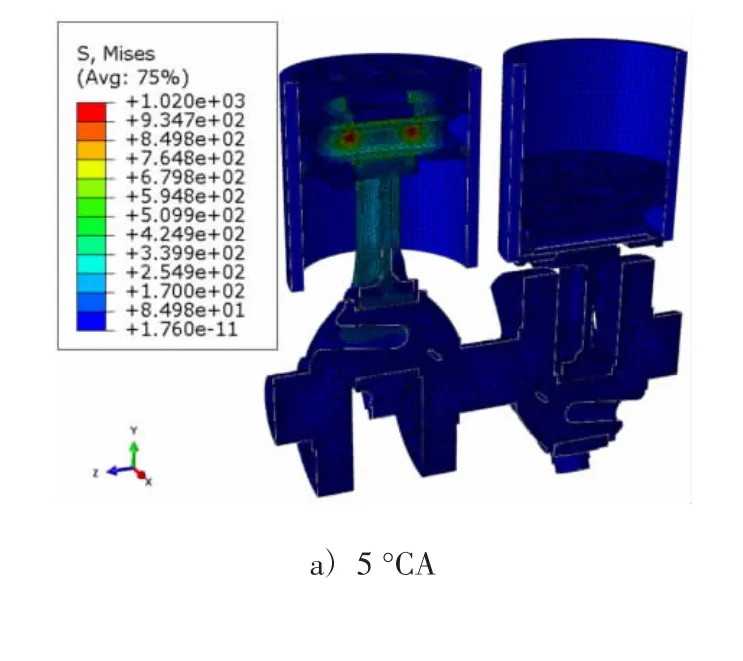
图7 曲柄连杆机构在5°CA、40°CA及75°CA时应力分布

图8 曲轴部件在5°CA、40°CA及75°CA时应力分布

从图8a知，曲柄销减重孔、曲柄销和曲柄臂连接处及主轴颈支撑点应力较大，最大为287.4 MPa，远小于曲轴材料Cr40的屈服极限，因此在最严苛工况下曲轴仍满足强度要求。曲轴在工作中承受周期性动载荷，因此不仅要考察应力最大点，更应注意应力梯度较大的位置，这些位置容易产生振动和疲劳[23]，是曲轴最易破坏的区域。考察曲拐中面曲柄臂的应力梯度，如图9所示。作一个循环内曲柄臂应力梯度曲线图，如图10所示，应力梯度与缸内压力趋势基本一致，在最高爆发压力下应力梯度最大，为121.97 MPa。可以看出，一个循环内曲拐中面的应力梯度变化较大，容易在曲柄臂圆角处产生疲劳破坏。

连杆在上止点后5°CA、40°CA及75°CA的应力分布如图11所示。

图9 曲拐中面应力梯度云图

图10 曲拐中面应力梯度循环曲线图

图11 连杆在5°CA、40°CA及75°CA时的应力分布

由图11可知，连杆小头承压部位由于活塞销变形引起边缘效应，边缘超出许用应力，优化措施是在小头内孔边沿作1×45°倒角，并采用局部硬化的热处理，减小应力集中。对装配了优化后的连杆机构进行计算，连杆小头应力分布对比如图12、图13所示。

图12 结构优化前应力分布

图13 结构优化后应力分布

由图13可知结构优化后连杆应力分布正常，小头孔下边沿最大应力为407.43 MPa，小于42CrMoV材料588 MPa的屈服极限，实际连杆还需热处理喷丸等强化工艺。连杆是二力杆，对变形较为敏感，长度方向变形量不能超过20μm，否则影响发动机装配和正常运作。如纵向变形过大不仅引起衬套咬合甚至可能发生活塞碰气门等故障。任意节点实际位移=刚体位移+变形位移，因此考虑两点的变形时须找一中性基准点，此点只有刚体位移而没有变形位移，选择所关心点的绝对位移与中性点绝对位移的差便是该点的变形量。以5°CA曲轴转角为例，选取连杆上具有代表性的小头节点、大头上端节点的变形数据，处理得到两点基于中性点的变形量，如图14所示。

由图14曲线知，连杆变形量基本符合要求，不影响发动机的装配和正常工作，同时又做到了连杆的轻量化。

运动副载荷以1#缸为例，在5°CA、40°CA及75°CA转角下曲柄销的载荷大小分别为31 705.19 N、9 456.52 N和2 514.7 N，活塞侧推力大小分别为763.56 N、1 554.91 N和724.04 N，与理论计算结果符合较好。

图14 连杆纵向变形量曲线

3 结果对比分析与讨论

3.1 发动机GT-POWER与ABAQUS动力学分析结果的对比验证

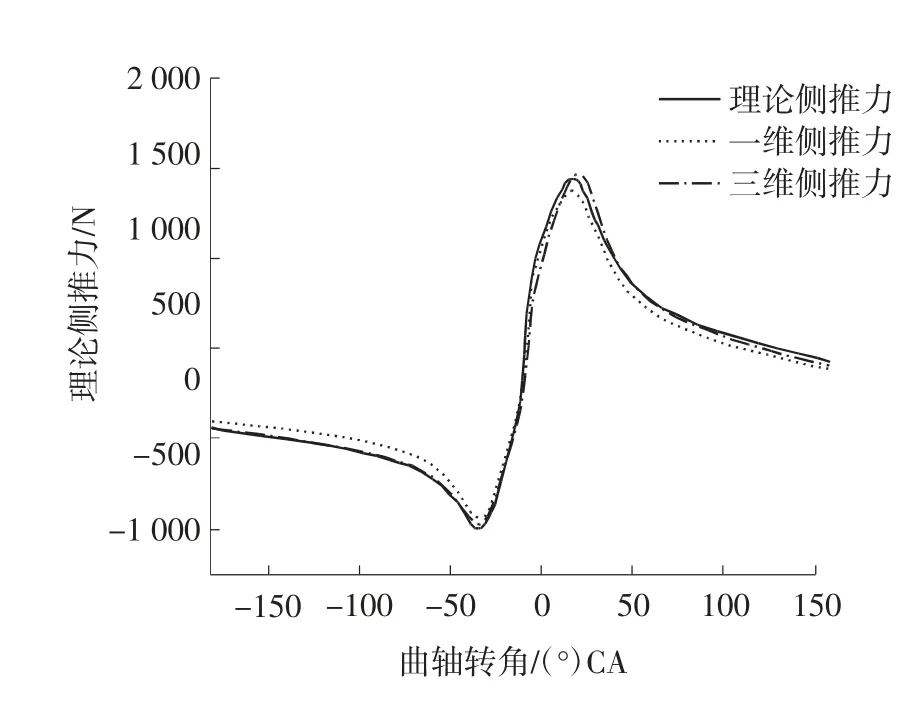
图15 活塞侧推力的一三维载荷曲线

二冲程为平面曲轴，两缸载荷的分析结果大小方向一致，仅相位差180°CA，因此仅以1#缸作分析。

提取GT-POWER动力学分析结果及对ABAQUS分析结果后处理，得到1#缸活塞侧推力及曲柄销载荷在一个循环内的一三维结果对比，如图15、图16中曲线所示。理论计算与基于ABAQUS的分析在大小和方向上基本一致，GT-POWER的一维分析与三维的ABAQUS在趋势上符合较好，但与理论结果差异较大，如图17所示，最大差异在3%左右。其原因主要是两种计算方法的不同，基于有限元的ABAQUS动力学分析相对假设条件较少，且网格划分合理时其误差主要来源于截断误差；一维动力学分析需输入较多设定参数，其中一些参数根据同级别发动机采用经验值，或在计算零部件惯量等参数时对几何模型做了简化。因此由于条件限制GTPOWER采用了较多的假设及简化，使计算结果出现较大误差。但相对理论或三维结果，其平均偏差保持在3%以内，对精度要求不高的分析仍具有一定参考意义。

需注意的是1#缸活塞侧推力在一个循环内有两个峰值，这对发动机平衡性和动力输出特性都是有害的，可加装飞轮甚至平衡轴来改善。GT-POWER与ABAQUS关于1#缸曲柄销载荷的分析结果相符较好。通过ABAQUS对发动机动力学分析，可得到曲柄销整环的应力分布，应力最小位置适宜布置润滑油孔，从而改善曲柄销的润滑条件，使油膜更容易形成，提高发动机的使用寿命。

图16 曲柄销载荷的一三维载荷曲线

图17 不同载荷形式一三维结果差异曲线

3.2 曲柄连杆机构最大应力分布曲线

曲柄连杆机构由不同材料部件组成，不同材料屈服极限也有较大差异，应力大小对于材料的强度刚度是与材料紧密相关的。研究40Cr的曲轴，分析其应力大小及其位置，提取曲轴一个循环内每个计算点的最大应力，判断其每一曲轴转角下的可靠性。可得如图18所示的最大应力与曲轴转角曲线。

图18 40Cr曲轴的最大应力曲线

由于采用的是基于“瞬时结构假定”的运动弹性动力学分析方法，因此图18曲线是由分布密集的有限个计算点拟合而成的样条曲线。通过后期增加的计算点的验证，其结果符合较好，通过该曲线可以预测一个循环内其他点的最大应力位置。

3.3 针对二冲程航空发动机的动力学结构设计改良方案

曲拐布置及点火正时、配气与供油系统的匹配，决定了二冲程发动机结构型式、运行方式与常见的四冲程发动机有较大差异。二冲程发动机一个循环曲轴旋转360°CA，而四冲程为720°CA，因此二冲程发动机运动副等所受交变载荷的频率是四冲程的两倍。同时造成热负荷比四冲程发动机高，总之二冲程发动机的运行工况更为恶劣。因此针对二冲程航空发动机的动力学结构设计具有更严苛的标准，不仅要求良好的配气、扫气及燃烧组织，同时针对动力学的分析应尽可能接近发动机真实的动力学过程，减少假设和简化，对重点区域详细分析。如转动副载荷的分析指导滑动轴承的结构设计，保证良好的压力润滑，提高发动机运行品质和寿命；侧压力的分析指导活塞裙部型线的优化，使活塞在正常运行中形成良好的楔形油膜，从而延长缸套寿命和提高发动机的效率。

4 结论

1）在热力循环的基础上，基于GT-POWER的动力学分析，更侧重部件间运动副载荷大小随曲轴转角的变化规律，对发动机在整个循环内的载荷分布有直接的反映；基于有限元理论，应用运动弹性动力学理论的ABAQUS动力学分析，更注重某个瞬态的应力分布和部件的变形情况，对部件每一部分受力有更详细的分析。GT-POWER与ABAQUS结果误差保持在3%以内。

2）GT-POWER的示功图等输出参数可作为ABAQUS分析的载荷边界条件。GT-POWER与ABAQUS的联合仿真，结合一维分析计算速度快及三维分析计算精度高的优势，对特定动力学过程进行重点分析，不仅可以得到三维非线性分析的精确结果，同时可减少三维计算量，节约计算成本。

3）一维和三维结合的动力学分析方法虽在满足精度的同时减少了计算量，但目前无试验数据与之对比验证。对于联合仿真结果的试验数据验证以后可以进一步作深入研究。

4）联合仿真结果可指导结构设计及优化。如在连杆小头内孔边沿作1×45°倒角后，最大应力由边沿效应引起的超过1 000 MPa降为407.43 MPa，连杆纵向变形量小于20μm，保证了发动机的正常运转；最高爆发压力11 MPa下，曲柄销载荷最大为31 705.19 N，活塞侧推力为763.56 N，根据计算结果，可指导曲柄销压力润滑油孔位置确定，保证发动机良好润滑，从而提高了寿命，同时根据侧推力可为发动机倾覆力矩的平衡提供参考，优化发动机的动力学输出特性。