土工格室加筋砂土试验颗粒流分析

卢少可, 夏小和, 张孟喜, 杨纪芒

(1. 上海大学土木工程系, 上海200444; 2. 同济大学土木工程学院, 上海200092)

随着现代社会进步, 道路、铁路、桥梁等基础道路设施在人们的生活中扮演者越来越重要的角色, 因此对工程的质量、进度、精度等要求也不断提高, 研究土与加筋材料之间的界面特性及其加筋机理成为当前学者关注的热点. Fabian 等[1]通过不排水3 轴试验研究了土工织物的加筋效应. 土工格室因其具有较高的侧向限制和抗滑、防变形、可有效提高土体的承载能力和分散载荷等特点得到了较为广泛的应用. 目前, 关于加筋土工格室的加固机理、强度特性研究和数值模拟等方面都取得了较大的进展, 尤其是在加筋土工格室的应用方面, 如加筋土工格室地基、挡土墙、路堤等.

3 维颗粒流分析程序(three dimension particle flow code, PFC3D) 利用圆形颗粒或利用圆形颗粒组成的非圆形颗粒组来模拟其运动和相互作用, 以此来研究颗粒介质的特性和作用机理. Imre[2]对边坡稳定性问题进行了数值模拟分析; 张孟喜等[3]对于水平-竖向加筋在挡土墙中的作用机理进行了研究; 周健等[4]进行了砂土双轴实验的颗粒流模拟; Potyondy 等[5]利用PFC2D研究了岩石的接触问题; 柴浩等[6]对扩径桩抗压性能的颗粒流数值进行了模拟; 周健等[7]进行了砂土中静压桩沉桩过程试验研究与颗粒流模拟; 王艳丽等[8]研究了饱和砂土的动力特性; 黄博等[9]研究了高速列车荷载作用的动态3 轴试验模拟; 谢婉丽[10]在GDS 高级动态3轴测试系统上针对在不同加筋层数、不同围压和不同动应力作用下的动态3 轴进行了试验; 李识博等[11]进行了黄土3 轴试验的颗粒流模拟; 刘勇等[12]进行了粗粒土的3 轴试验颗粒流模拟;孙洲等[13]对条形荷载作用下土工格室加筋砂土路堤模型进行了试验和分析; 李丽华等[14]研究了轮胎与格室加筋路堤性能和承载力; 汪海年等[15]进行了土工格室加筋碎石基层变形机理的数值模拟.

以往学者对加筋土的研究大多局限于宏观层次, 而对在受力过程中加筋结构土体与加筋材料的位移和接触关系, 以及其他相关的细观参数变化的研究较少. 本工作将采用3 维颗粒流PFC3D软件, 通过追踪每一颗粒单元的运动轨迹得到颗粒间接触力与位移, 并利用PFC3D对试验进行仿真模拟, 以此来确定PFC3D对加筋砂土模拟的细观参数.

1 模型模拟

1.1 模型建立

3 轴试验仪器采用美国GCTS(Geotechnical Consulting and Testing Systems)公司研制的USTX-2000 非饱和土/饱和土动静3 轴测试系统, 并用该仪器的数据采集系统进行试验数据采集. 试验砂为福建标准砂(颗粒级配如图1 所示), 不均匀系数为2.07, 曲率系数为0.87, 其物理性质指标如表1 所示. 本试验采用静3 轴固结不排水, 分别在不同的围压下进行试验, 从而得到砂样破坏时的参数.

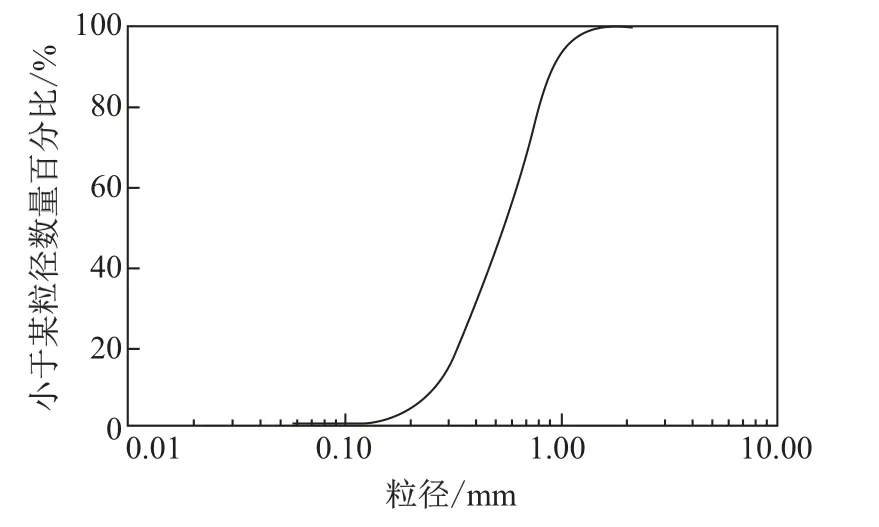
图1 试验所用砂颗粒级配曲线Fig.1 Grain size distribution curves of sand used in tests

表1 试验砂样的物理特性参数Table1 Physical parameters of sand

1.2 试样制备

颗粒流模拟的接触模型选用接触刚度模型, 颗粒之间的黏接关系采用接触黏结方式. 筋材的模拟采用抗弯性能较好的平行粘结模型. 由图1 的级配曲线可知, 3 轴试验中砂颗粒直径在0.5∼1.0 mm 范围内的颗粒数量所占百分比最大, 因此颗粒直径应该以此范围为主. 由于颗粒半径太小, 且受计算速度和颗粒数量的限制, 故最终选择颗粒直径为2.5∼5.0 mm. 通过反复对比试验与数值模型的结果, 不断调整颗粒间的细观参数, 使宏观力学特性与细观参数模拟结果相吻合, 说明选取的细观参数是合理的, 这样就可以用颗粒流数值模型来模拟实际试样. 纯砂模型的应力-应变(σ1-σ3)曲线如图2 所示, 砂土颗粒与筋材颗粒细观参数如表2 所示.

图2 纯砂模型应力-应变曲线Fig.2 Stress-strain curves of sand

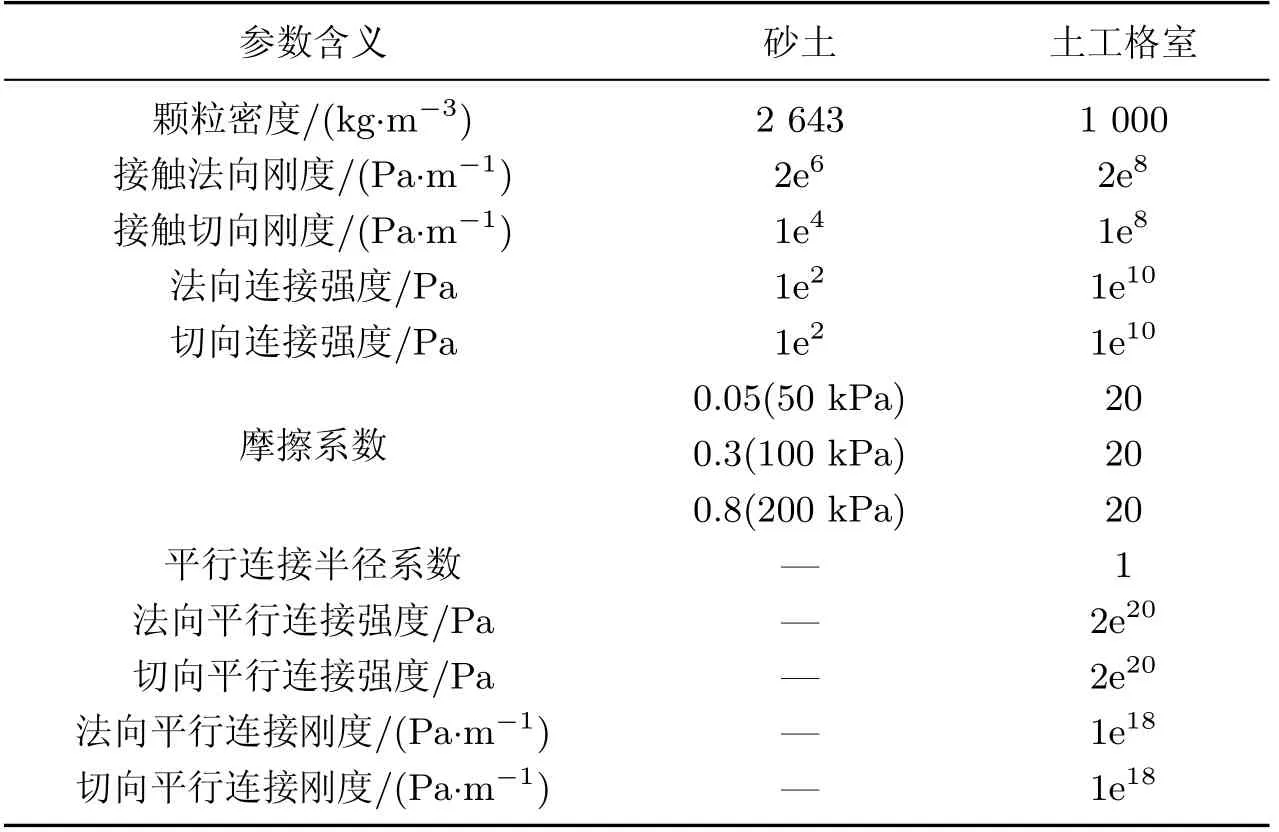
表2 PFC3D模型细观参数Table2 Micro parameters in PFC3D mode

1.3 模型生成

加筋土工格室模型的生成顺序是墙体、土体颗粒、土工格室, 具体步骤为①生成3 道没有摩擦力的墙体作为试样的边界, 3 轴试验的尺寸为100 mm×220 mm; ②在墙体边界内按照半径扩大法生成土体颗粒, 再施加重力使土体颗粒达到平衡; ③删除布置土工格室位置的土体颗粒. 这里, 土工格室是用许多圆形颗粒来模拟, 通过赋予颗粒与颗粒之间足够大的摩擦力,以保证筋材颗粒在加载时不会脱落; 土工格室之间采用平行连接, 使筋材颗粒能承受弯矩和力. 采用生成土体颗粒的方法在土工格室的位置生成土工格室; 然后在土工格室的内部再生成土体颗粒; 最后再施加重力, 使加筋土工格室内部达到平衡.

在生成模型后, 通过伺服机制来控制墙体的移动速度给试样加载, 采用同样的方法给颗粒施加围压. 试样破坏的标准为①存在峰值时以σ1-σ3的峰值点为破坏点; ②无峰值点时, 取轴向应变为15%时的主应力差峰值点. 筋材和砂土模型如图3 所示, 其4 种工况如表3 所示(模型直径为100 mm, 土工格室的间距为55 mm).

2 土工格室加筋砂土的细观模拟分析

2.1 加筋砂土的应力-应变

首先, 建立纯砂土模型, 在纯砂的基础上建立土工格室模型(见图3). 在50 kPa 条件下进行静载试验模拟(见表3), 土工格室加筋砂土的偏应力-轴向应变曲线与试验曲线的对比如图4 所示. 图4 中方形代表PFC 模拟结果, 圆形代表试验结果.

图3 筋材和加筋砂土模型Fig.3 Model of reinforcement and reinforced sand

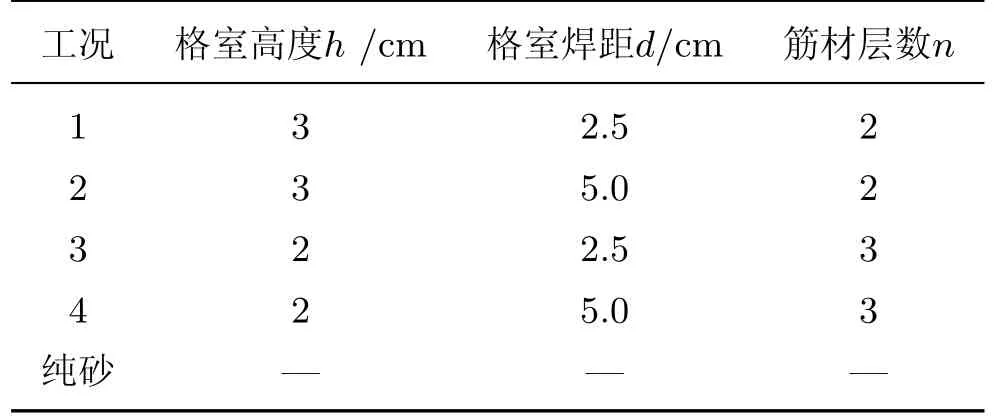
表3 试验工况Table3 Test conditions

图4 是在σ3=50 kPa 时土工格室加筋土的应力-应变曲线图. 由图可知, 工况1∼4 的试验得到的极限承载力(偏应力)为800.27, 841.21, 617.49 和623.04 kPa. 比较工况1 和2, 发现土工格室的高度不变, 焊距减小2.5 cm, 土工格室极限承载力提高了5.15%; 比较工况2 和4, 土工格室焊距不变, 高度增加3 cm, 土工格室的极限承载力提高至25.84%. 可见, 土工格室的焊距和高度对于加筋的效果都有显著的影响, 格室焊距减小和高度增大都会使加筋砂土的承载力增大. 可见, 土工格室高度越高, 格室与土体颗粒的接触面积就越大, 即摩擦力越大, 承受载荷的能力也越大; 如果土工格室焊距过大, 会导致单个土工格室内承受的水平载荷过大, 最外侧的格室更容易受拉破坏, 导致承载力降低.

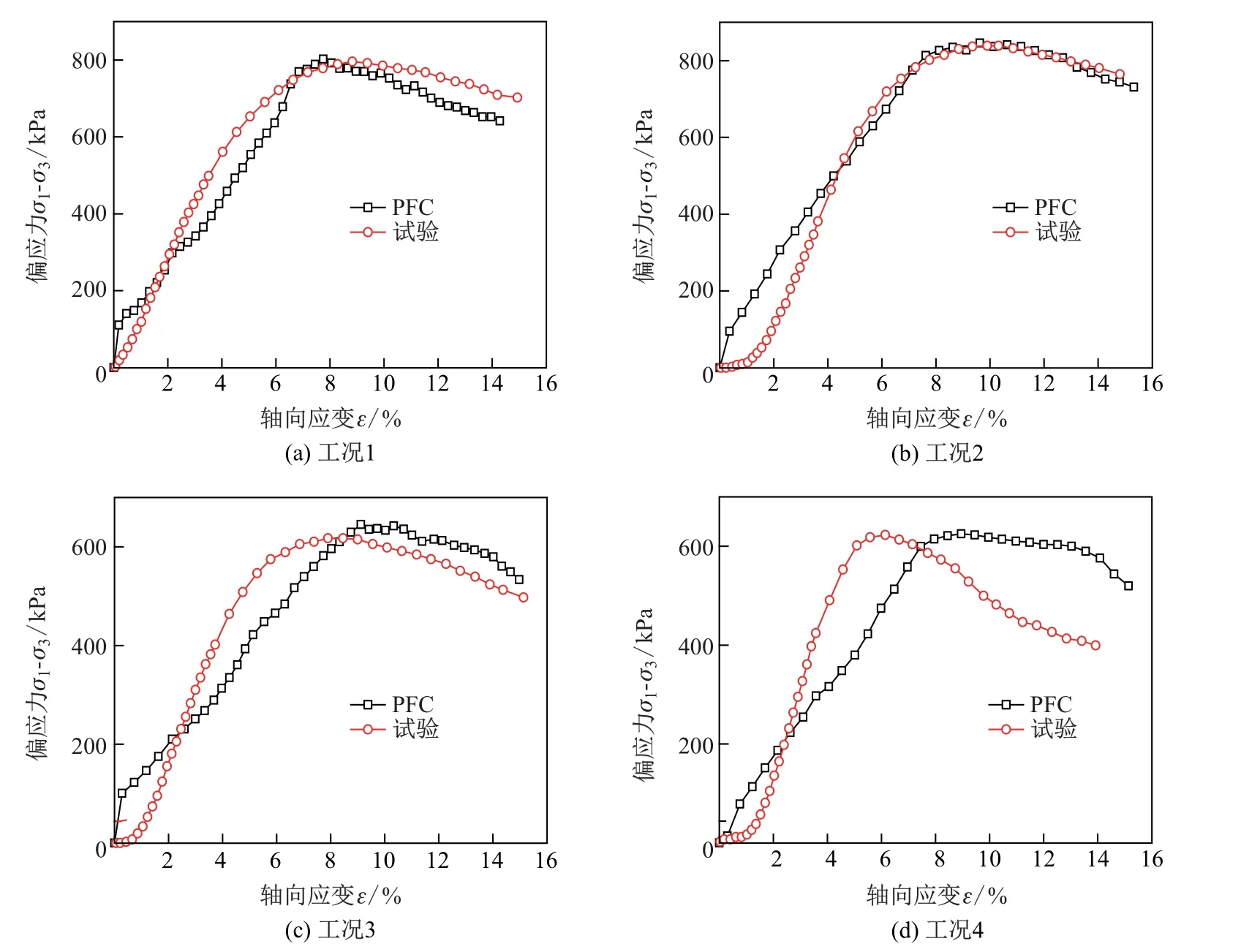
图4 σ3=50 kPa时土工格室加筋砂土应力-应变曲线Fig.4 Confining pressure 50 kPa formula geocell reinforced sand by stress-strain curves

由图4 还可以发现, 4 种工况下的试验曲线和模拟曲线的拟合度较高. 在初始阶段产生相同的应变值时, 模拟偏应力大于试验曲线值, 这可能是因为试样在加载初期有一个压密过程,即在模拟过程中试样在加载前已经进行了土体压密. 但是, 在经历了前期的压密过程之后, 试验曲线中的偏应力随应变增大的速度明显比模拟曲线值快, 这是因为在PFC 模拟土体和加筋材料时, 都是用球体来代替实际材料颗粒, 并且PFC 中材料与材料之间的相互作用只能根据摩擦系数来调整, 所以想要实际模拟土体与筋材之间的界面性质还是有一定难度的, 但在此基础上可以实现定性的分析.

图5 为当σ3=100 kPa 时土工格室加筋砂土的模拟偏应力-应变曲线图. 从图中可以发现,在试验开始阶段强度提升比3 轴试验的模拟曲线快, 但是在应变达到3%后, 试验曲线中偏应力随应变增大的速度比模拟曲线的快. 在进入峰值应力前对于工况1 来说差别较大, 但是达到的峰值应力基本一致, 且过后曲线的拟合度较高, 说明PFC3D模型能较好地模拟土工格室加筋砂土3 轴试验.

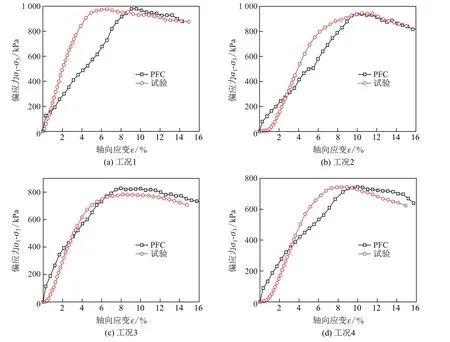
图5 σ3=100 kPa时土工格室加筋砂土模拟偏应力-应变曲线Fig.5 Confining pressure 100 kPa formula geocell reinforced sand by stress-strain curves

通过对比分析各种工况下试验达到应力-应变曲线的峰值点与试验模拟得到的峰值点、对应的应变值, 以及未加筋的情况(见表4), 发现所得的极限承载力与模拟得出的极限承载力非常接近, 相应的应变值也较接近. 有3 组试验得出的极限应变相差较大, 但极限承载力非常接近, 在应变要求不高时可采用. 因此, 本工作后续可用PFC 进行有关土工格室力学特性的分析和验证. 最后, 分析对比了在载荷作用各个围压下纯砂模型的极限承载力, 可以看出土工格室加筋砂土的极限承载力相较于纯砂极限承载力, 均有不同程度的提高, 最大的提高了61.65%,说明土工格室对于提高砂土承载力有着显著的作用.

2.2 接触力分布变化关系分析

在PFC3D软件中, 力主要通过颗粒-颗粒和颗粒-墙之间来传递. 为了分析土工格室加筋土的工作机理, 本工作对颗粒-颗粒之间的接触力情况进行了研究. 图6 为土工格室加筋砂土PFC3D试验在围压为50 kPa、格室高度为3 cm、结点间距为2.5 cm 时的颗粒接触力分布图.

图6 中, 黑线表示接触力为压力, 红线表示接触力为拉力, 线条的宽度代表接触力的大小.图中的线框表示加筋的上下界限. 从图中可以发现, 加筋土试样在ε=0 时, 加筋土模型内颗粒之间的接触力全部为压力, 并且大部分平行于加载方向, 颗粒与墙体之间的力垂直于墙体. 持续加载, 在ε=5%时由土工格室的受力特性可知, 土工格室会将上部分的竖向荷载转化为水平力作用在各个土工格室上, 格室之间的侧向力大小相等, 方向相反, 故可以发现在加筋部位颗粒与颗粒之间的接触力比未加筋区的大而集中, 且方向水平, 在土工格室的影响区域内这种现象较明显. 另外, 在土工格室内部形成的圆柱状的加强区, 即“环箍”作用, 主要承受上部分传来的荷载, 从而导致颗粒与墙体之间接触力减少, 阻止土体的侧向变形. 随着变形进一步扩大,在ε=10%时土工格室的抗拉强度高和抗侧向能力强的特点充分发挥, 此时“环箍”作用更明显,格室间的侧向移动受到了限制. 在未加筋的底部土体颗粒之间的接触力既有压力又有拉力, 但是在加筋部位几乎没有拉力存在, 说明土工格室加筋有效承担了土体中的拉力, 提高了土体强度, 土体变形得到了控制.

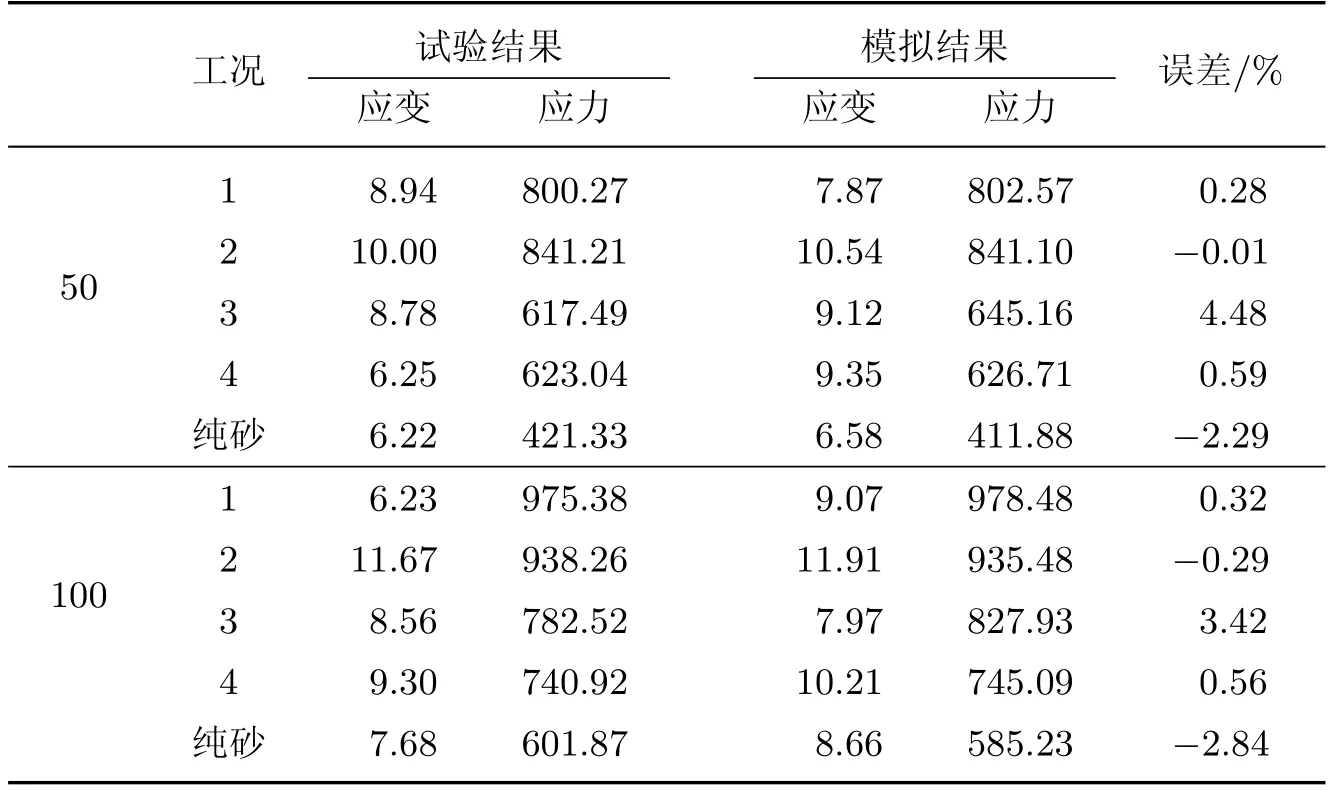
表4 试验与模拟极限承载力对比Table4 Comparisons of test and simulation ultimate bearing capacity

图6 σ3=50 kPa时土工格室加筋砂土颗粒接触力分布Fig.6 Confining pressure 50 kPa formula geocell reinforced sand particle contact force distribution

2.3 位移分布变化关系分析

图7 为土工格室加筋砂土PFC3D试验在围压为50 kPa、格室高度为3 cm、结点间距为2.5 cm 时的位移力分布图. 由图可以看出, 当ε=5%时由于侧向受到土工格室的影响, 上层加筋及影响区域内的颗粒逐渐向土工格室中间聚集, 且随着应变的增大这种趋势越来越明显. 在ε=10%时土体颗粒的位移方向基本上是在土工格室中间, 形成类似柱状的位移集中区域. 土体颗粒的排列越来越整齐, 并且都沿着σ1方向, 而土工格室外面的土体未受到土工格室的限制, 颗粒逐渐向外扩散.

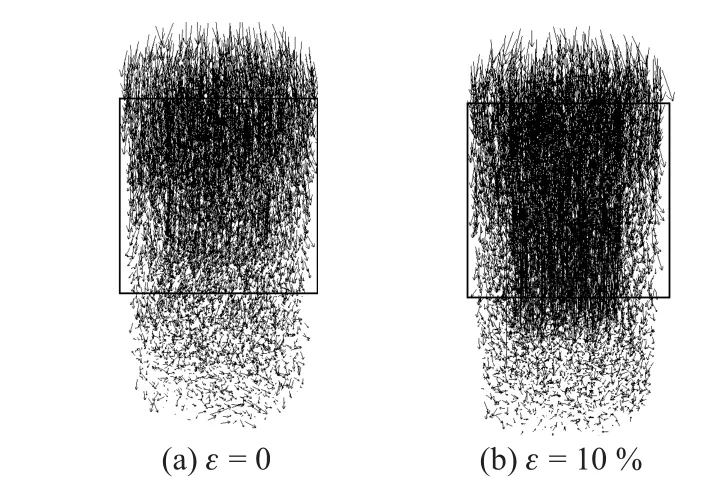
图7 σ3=50 kPa时土工格室加筋砂土颗粒位移分布Fig.7 Confining pressure 50 kPa formula geocell reinforced sand particle displacement distribution

2.4 孔隙率变化分析

图8 显示了加筋砂土加载过程中孔隙率的变化情况. 通过对比格室内部和外部的孔隙率可以发现, 格室内部的土体颗粒由于受到格室的限制, 在外部荷载作用下达到平衡时孔隙率较低, 并且达到平衡所需时间较少; 模型不同高度的孔隙率是不同的, 距模型底部越远, 最终平衡时孔隙率越低.

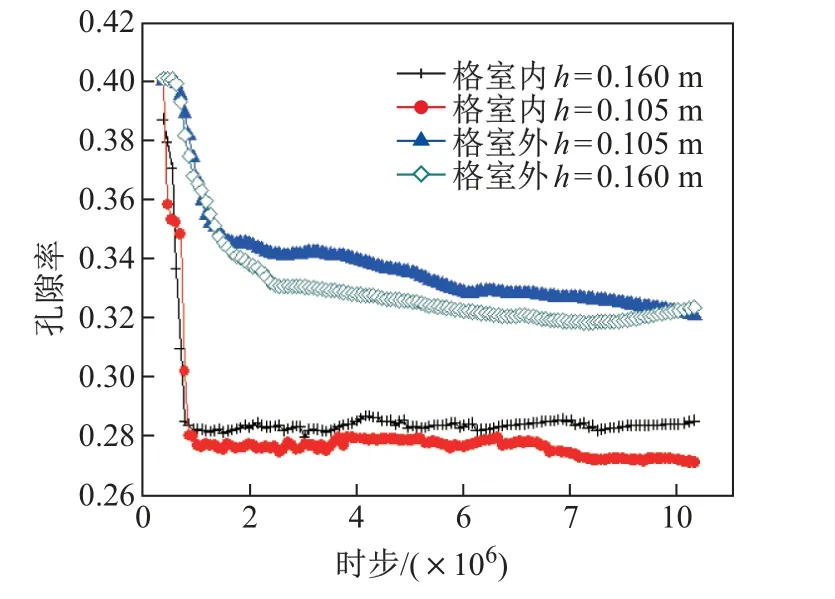
图8 土工格室加筋砂土的孔隙率变化Fig.8 Change of porosity of geocell reinforced sand

3 结 论

本工作在纯砂和土工格室加筋砂土静载3 轴试验的基础上, 采用PFC3D进行静载3 轴试验数值模拟, 在得到宏观力学行为的同时, 从细观角度上分析了土工格室加筋砂的作用机理,得到如下结论.

(1) 用PFC3D进行砂土的静载3 轴试验的模拟方法是可行的, 选用的接触模型和黏接模型是合理的, 纯砂的模拟结果与试验结果能够较好地吻合.

(2) 在纯砂模型的基础上, 运用PFC3D可以对土工格室加筋砂土进行较好的模拟, 在低围压情况下加筋砂土模型的应力-应变曲线与试验得到的结果基本吻合.

(3) 当土工格室加筋砂土轴向压缩时, 由于受到土工格室的限制, 颗粒间的受力方向随着应变的增大逐渐发生了改变, 在加筋区形成柱状加强区的土体颗粒承载力增大, 极限应变增大. 随着应变逐渐增大, 土工格室内部及其影响区域内的颗粒在位移方向排列整齐, 基本沿着主应力σ1方向; 格室外部的土体颗粒向四周扩散.

(4) 随着加载的进行土工格室内部的土体颗粒较外部的先达到平衡, 并且当平衡时土工格室内部的孔隙率比格室外部的低.