基于成本“粘性”下的投资组合模型
蔡宇欣, 任永平
(1. 上海大学管理学院, 上海200444; 2. 复旦大学管理学院, 上海200433)
1952 年, Markowitz[1]提出了以方差为风险度量的均值-方差(mean variance, MV)投资组合模型, 该模型的核心是在一定的投资收益水平下, 选择风险最小的投资组合或在投资者能够承受的风险程度内追求最大期望收益. 虽然该模型一直被视为现代金融理论的基石, 是很多重要理论的基础, 但在实际应用中, 由于假设条件不满足或计算太复杂而较少被直接当作解决大规模投资组合问题的工具. 为了简化计算量, Konno 等[2]提出了以绝对偏差替代方差来度量风险, 建立了均值绝对偏差(mean absolute deviation, MAD)模型, 该模型解决了由方差计算带来的困难并保留了均值-方差模型的优点. 虽然收益率高于期望收益率那部分偏离了期望, 但是这部分波动实质上并不构成实际的损失, 故应用半绝对偏差来控制投资组合风险的思想被提出. 1998 年, Young[3]提出以半绝对偏差为风险度量的考虑交易费用流动性的线性规划模型,该模型运用极小极大值原理, 考虑最差行情下的损失来规避极端的风险. 这些方法从数学的角度考量了投资组合风险的度量, 但较少考虑资本市场作为实体经济的表现形式, 以及本身具有的经营风险. 现代投资理论认为, 投资组合问题本身是一个收益与风险的权衡问题, 忽略各投资标的本身特点的投资组合的风险计量是不准确的[4]. 由于各行业与各企业本身存在共性与个性, 各企业的企业文化、经营管理效率、盈利能力等都不尽相同, 故这些个性都将影响投资组合的选择、风险收益率及投资组合的盈利预测[5]. 如何度量实体经济本身存在的财务风险成为必须解决的问题. 因此, 本工作引入企业的成本“粘性”来控制企业本身存在的盈余能力, 这是因为企业盈余能力的高低是企业获得竞争优势的软实力, 高质量的盈余可以帮助企业有效提升运营绩效, 把握市场投资契机, 提高资本配置效率, 降低企业潜在风险及损失[6]. 本工作试图在考虑投资组合风险的基础上, 结合企业自身的财务风险, 使得投资者在资本市场中能更准确、更有效地选择投资组合标的, 为其提供更具实用价值的资产配置组合方法.
1 研究假设与设计
1.1 研究假设
净资产收益率是企业盈利能力的核心指标, 也是杜邦财务指标体系的核心, 更是投资者关注的焦点. 一般来说, 如果企业的净资产收益率在一段时间内持续增长, 说明其资本盈利能力稳步上升. 但是, 净资产收益率不是一个越高就越好的概念, 还需注意企业的财务风险. 上市公司单纯通过加大举债提高权益乘数, 从而提高净资产收益率的做法是十分危险的. 单纯增加负债对净资产收益率的改善只具有短期效应, 最终将因盈利能力无法涵盖增加的财务风险而使企业面临财务困境. 因此, 只有当企业净资产收益率稳步上升、财务风险没有明显加大时,才说明企业的财务状况是良好的.
在国外,Anderson 等[7]运用大样本数据证明了成本存在明显的“粘性”行为,成本“粘性”的变化不仅取决于净资产收益率的高低, 而且还与净资产收益率的变化方向及速度有关; Banker等[8]构建了考虑成本“粘性”的盈利预测模型, 发现其盈利预测的精确度高于传统的盈利预测模型; Weiss[9]检验了成本“粘性”与分析师盈利预测模型之间的关系, 发现当企业的成本“粘性”水平较高时, 企业的财务风险较大, 分析师对其盈利预测精确度也相应较低.
在国内, 已有学者自2003 年起对成本“粘性”展开了一系列的研究. 孙铮等[10]对中国综合A 股市场292 家上市公司的财务数据进行实证检验, 发现上市公司确实存在成本“粘性”; 王明虎等[11]通过建立数理研究发现, 公司成本“粘性”与自由现金流量的多少有关, 而自由现金流量对企业的经营风险起决定性作用.
“粘性”的存在不仅影响了企业净资产收益率的稳步上升, 而且还与企业的财务风险正相关. 为了在资本市场中能更准确有效地选择投资组合标的, 为投资者提供更具实用价值的投资组合方法, 考虑成本“粘性”下的投资组合是否能有效提高投资者的投资回报呢?由此, 本工作提出如下2 大假设:
假设1 考虑成本“粘性”下的MV(cost stickiness MV, CSMV)投资组合模型下的收益率比传统的MV 投资组合模型表现好;
假设2 考虑成本“粘性”下的MAD(cost stickiness MAD, CSMAD)模型的收益率表现明显优于传统的MAD 模型.
为了检验假设1 及假设2, 本工作选用2006—2015 年上市公司公布的财务数据为研究对象, 数据来源于国泰安数据服务中心及万得金融资讯终端. 首先, 对上市公司的成本“粘性”进行量化;其次, 考虑CSMV 及CSMAD 模型的理论基础及模型的适用条件.
1.2 成本“粘性”的计量
考虑资产的成本“粘性”, 须采用Anderson 等[7]提出的回归模型, 该回归模型为
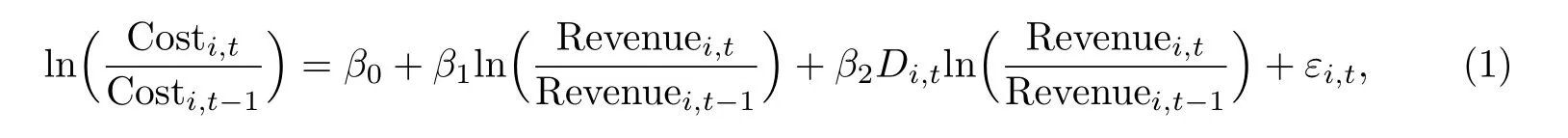
式中, Costi,t为第i 家公司在第t 年支出的成本费用; Revenuei,t为第i 家公司在第t 年获得的销售收入; Di,t为虚拟变量, 即当第t 年的销售收入低于第t−1 年的销售收入时取1, 当第t 年的销售收入高于第t−1 年的销售收入时取0. 根据成本“粘性”的定义, 即成本随销售收入变化时具有不对称性, 可以合理预计; 如果上市公司存在成本“粘性”, 则应有β1>β1+β2, 从而推断出β2<0(如果β1>0), β2越小, 资产的成本越“粘”. 这样, 成本“粘性”得到有效量化.
1.3 模型的理论基础
假设金融市场中有n 个风险资产, 考虑每个资产在成本“粘性” β2下的均值-方差的理论基础. 记Rj(j = 1,2,··· ,n)为资产Sj的随机收益率, xj为资产Sj的投资比例, 则投资组合x=(x1,x2,··· ,xn)的资产回报为

假设收益分布是离散的, 且有T 种可能的收益情形; 假设每种情形发生的概率相等, 则每种资产的平均收益为表示为第j 种资产的成本“粘性”的大小, 令r(x),u(x),v(x)分别为均值、绝对偏差和方差, 则有

为了计算投资组合模型的基数约束, 引入0-1 决策变量dj,

令投资组合的容许约束集合为
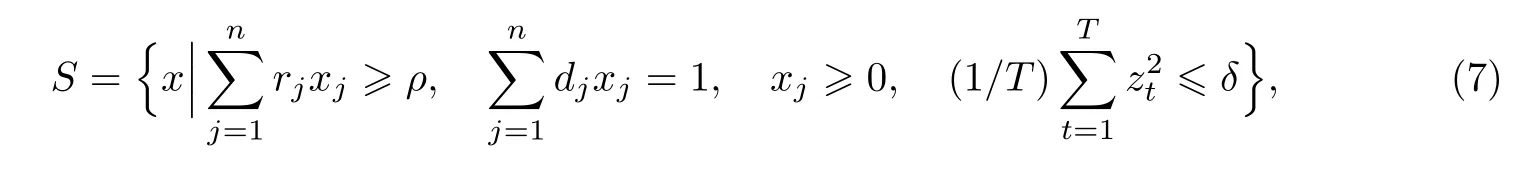
式中, ρ 为预期收益, δ 为给定的方差, 则CSMV 模型及CSMAD 模型可表示为

显然, CSMAD 模型也是一个凸优化问题, 且比CSMV 模型更易得到全局最优解.
基于CSMV, CSMAD 模型的有效性与MV, MAD 模型一样, 必须满足2 个条件[1]: ①随机收益率满足正态分布的条件; ②效用函数至少是2 次函数, 以保证期望与方差可求. 本工作通过对中国综合A 股市场历史数据的年收益率、月收益率、周收益率和日收益率做正态性检验. 显然, 只有当中国证券市场适用于MV, MAD 模型时, CSMV 及CSMAD 模型才能适用.
1.4 综合A 股市场收益率的正态分布性检验
对综合A 股市场的考虑现金红利再投资的综合市场收益率(等权平均法)、不考虑现金红利再投资的综合市场收益率(等权平均法)、考虑现金红利再投资的综合市场收益率(流通市值加权平均法)、不考虑现金红利再投资的综合A 股市场收益率(流通市值加权平均法)、考虑现金红利再投资的综合A 股市场收益率(总市值加权平均法)、不考虑现金红利再投资的综合A 股市场收益率(总市值加权平均法)6 种计算收益率方法进行正态性检验与分析. 利用Skewness/Kurtosis (S/K)法、Shapiro-Wilk (S-W)法及Shapiro-Francia (S-F)法对指数的年收益率、月收益率、周收益率和日收益率进行正态分布检验, 选用计量经济软件Stata 13.0 进行检验, 结果如表1 所示.
从表1 及图1 中可以看出, 在6 种计算收益率方法下, 综合A 股市场的年、月收益率的3种正态分布检验值均大于0.05, 这表明不具备拒绝原正态分布假设的条件, 需要接受原正态分布假设, 即2004—2015 年综合A 股市场的年、月收益率具有正态性, 该样本的年、月收益率适用于MV, MAD 模型及CSMV, CSMAD 模型. 而综合A 股市场的周、日收益率的3 种正态分布检验值均为0, 需要拒绝原正态分布假设, 即10 年综合A 股的周、日收益率不具有正态性, 这意味着该样本的周、日收益率不适用于MV, MAD 模型及CSMV, CSMAD 模型. 因此,本工作只对适用于MV, MAD, CSMV 和CSMAD 模型的样本进行实证分析, 以证明改进的CSMV, CSMAD 模型的有效性. 这也从另一个侧面表明, MV, MAD, CSMV 和CSMAD 模型只适用于当时间跨度较长时挑选最优化投资组合, 而并不适用于短期的优化投资组合.
2 实证结果分析
检验假设1 和假设2, 需对比MV, MAD, CSMV 和CSMAD 这4 种模型的有效性, 选取满足其使用条件的样本进行考察. 因此, 剔除有缺失及异常的样本, 剔除金融类及连续2, 3 年亏损的样本后, 选取综合A股市场各资产的年(月)平均收益率为测试样本及检验样本, 得到可用的样本量2 734 个及年、月测试检验值各27 340, 328 080 个. 检测方法采用后侧法, 方法如下:以样本中的2012—2013 年的年平均收益率为测试数据得到模型所需的参数和最优投资组合, 以2014—2015 年的年平均收益率作为检验样本检验最优投资组合的表现(可用不同时期样本运用同种方法反复进行). 以2011 年1 月4 日—2012 年12 月31 日的月平均收益率为测试数据得到模型所需的参数和最优投资组合; 以2013 年1 月4 日—2013 年12 月31 日的年(月)平均收益率为样本作为检验最优投资组合表现的稳健性, 稳健性的检验可选用不同时期的年(月)资产收益率数据, 运用同种方法反复进行测试. 模型均运用MatlabR2014b 对4 种模型进行求解, 得到各模型的全局最优解.

表1 综合A 股市场描述性统计及正态性检验Table1 Descriptive statistics and normality test of integrated A stock market
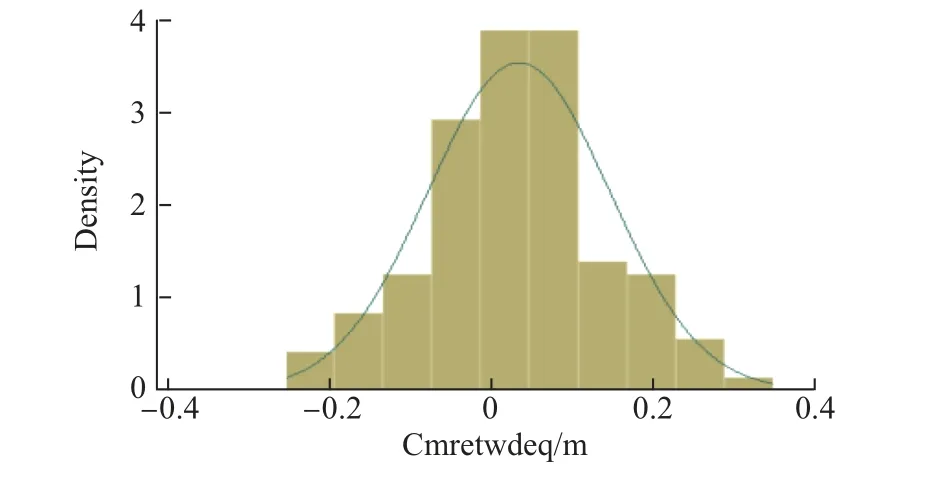
图1 综合A 股市场10年间月收益率分布Fig.1 Monthly yield distribution of integrated A stock market
本工作尽可能地在程序实现过程中使资产的投资组合范围最大, 那么模型的可行域范围需要最大化, 从而使投资组合的选择范围最大, 从而找到方差及绝对偏差最小值的可能性也最大. 令=k, 当n=2 734, k 取整数时, 即当引入决策变量时, 运用分支定界方法迭代10 000 次得到模型的近似最优解, 检验样本的最优投资组合表现如表2, 3 及图2, 3 所示. 当k取0 时, 意味着资产组合向量中n(n �2 734)个资产均被投资, 模型的计算简化为求线性规划的连续解, 即求解n 个资产的投资比例. 检验样本的最优投资组合表现如表4 及图4, 5 所示.

表2 MV模型及CSMV模型下的检验样本中投资组合收益率表现比较Table2 Portfolio yield performance comparisons of MV and CSMV models under the check samples of the portfolio yield

表3 MAD模型及CSMAD模型下的检验样本中投资组合收益率表现比较Table3 Portfolio yield performance comparisons of MAD and CSMAD models under the check samples of the portfolio yield

图4 MV模型及CSMV模型下n 取不同值时(k=0)投资组合年收益率表现Fig.4 Portfolio yield performance of MV and CSMV models under different values of n (k=0)

图5 MAD模型及CSMAD模型下n 取不同值时(k=0) 投资组合年收益率表现Fig.5 Portfolio yield performance of MAD and CSMAD models under different values of n (k=0)
由表2 可以看出, 由于MV 模型在k 取不同值时, 运行结果均为NaN, 表明不明确的数值结果, 显示该运算可能没有意义, 故CSMV 模型下的投资组合年平均收益率与MV 模型下的收益率不能比较, 但这能说明CSMV 投资组合模型优化了MV 模型, 使得在挑选投资组合时的计算变得有意义. 基于上市公司财务报告下的考虑成本“粘性”的风险投资组合优于不考虑成本“粘性”的投资组合的情况, 假设1 得证. 由图2 可看出, CSMV 模型在k 取较大值时, 投资组合收益率的波动趋于稳定. 有趣的是, 在假设各资产的平均收益率基本一致时, 挑选最优投资组合将演变成只考虑组合的方差风险, 而当协方差取最小值时, 就意味着各资产的相关性最小, 这从实证分析的角度说明了当各资产的收益率相近时, 应尽可能地挑选不同行业的资产进行配置, 从而达到投资风险最小的目的.
由表3 可以看出, 除当k=10 时MAD 模型下2015 年投资组合年平均收益率为4.431 0%,比CSMAD 模型下的收益率略高外, CSMAD 模型下的投资组合年平均收益率均比MAD 模型下的收益率高, 这说明CSMAD 投资组合模型优于MAD 模型. 考虑成本“粘性”下的风险投资组合优于不考虑成本“粘性”的投资组合, 假设2 得证. 由图2 和3 可以看出, 当k 取不同值时MV 模型与MAD 模型下的投资组合收益率的振幅较大, 而CSMAD 模型下的投资组合收益率的波动趋于稳定, 且比CSMV 模型下的投资组合收益率的波动更小, 这从一个侧面说明了CSMAD 模型可能比CSMV 模型更能起到避免投资者遇到如“业绩变脸”、“黑天鹅”等使收益率大幅波动从而影响投资者利益的事件.
由表4 及图4, 5 可以看出, 除当n=1 000 时MV 模型下2014 年投资组合年平均收益率比CSMV 模型下的收益率略高, 当n=100, 1 000 时2015 年投资组合年平均收益率比CSMV 模型下的收益率略高外, 其他数据均显示CSMV 模型下的投资组合年平均收益率比MV 模型下的收益率高, CSMAD 模型下的投资组合年平均收益率比MAD 模型下的高, 假设1 和2 得证.当n 取不同值时(k=0), CSMAD 模型下的投资组合收益率的振幅比CSMV 模型下的投资组合收益率振幅小, 这也说明了CSMAD 投资组合模型可能比CSMV 模型更能起到避免投资者遇到如“业绩变脸”、“黑天鹅”等使收益率大幅波动的事件. 当n 取不同值时(k=0), CSMV 模型下的投资组合年平均收益率比MV 模型下的高, CSMAD 模型下的投资组合年平均收益率比MAD 模型下的高. 虽然CSMAD 模型相对于CSMV 模型的计算较简单, 但当数据中0 表达较多时, CSMAD 模型在计算中存在一定的随机性, 这可能会导致CSMAD 模型的精确度降低, 但这并不代表在考虑上市公司其他反映财务风险的CSMAD 模型中仍会存在类似情况.从实证分析的角度看, CSMAD 模型可能更适合于中短期的投资组合风险配置. 限于篇幅, 表2∼4 只给出了测试样本2012—2013 年, 检验样本2012—2013 年、2014 年及2015 年的投资组合年收益率表现; 图2∼5 只给出了样本年投资组合收益率比较, 其他年份及月平均收益率表现或n 取其他资产个数时的收益率表现比较结果不在此赘述.
3 稳健性检验
本工作对CSMV,CSMAD 模型与MV,MAD 模型的有效性进行了稳健性检验和对比. 除对不同时期的年(月)平均收益率数据运用同种方法进行反复测试外, 还将A 股市场按证监会所分行业分类, 以各行业上市公司的年(月)平均收益率为测试样本及检验样本, 得到投资组合在CSMV, CSMAD 模型与MV, MAD 模型下的收益率表现进行比较. 最后为避免异常值的不良影响, 对同时期的年(月)平均收益率的测试样本进行缩尾处理, 即将样本值处于3%∼97%以外的极值样本进行Winsorize 处理, 并对处理后的数据再次进行投资组合收益率表现的比较, 得到的结果与前述研究结论基本一致, 表明本工作的研究结论是可靠的.
4 结束语
本工作利用S/K, S-W, S-F 这3 种方法检验综合A 股市场收益率的分布情况. 当综合A股市场收益率呈正态分布时, 考虑优化的资产投资组合模型, 建立了在MV, MAD 基础上的CSMV, CSMAD 模型. 实证分析结果表明:①CSMV, CSMAD 模型的检验样本收益率明显优于MV, MAD 模型, 即CSMV, CSMAD 模型优于传统的MV 和MAD 模型, 更适用于投资者寻求长期投资收益的最大化; ②对CSMV, CSMAD 模型与MV, MAD 模型的有效性进行了稳健性检验和对比, 结果表明本研究是可靠的; ③检验了综合A 股市场收益率的正态性, 但没有检验各资产的正态分布情况, 这样可能模糊了单个资产之间的差异, 而事实上各资产之间存在特征性差异, 这将是未来很有趣的一个研究方向.

