一种快反镜指向控制误差定量分析方法

冯甜甜，高晶敏，张科备

(1.北京信息科技大学 自动化学院，北京 100192；2.北京控制工程研究所，北京 100190)

0 引言

快反镜系统(fine steering mirror, FSM)是在激光光源与接收端之间进行光束调整的装置[1]。在现代激光通信、天文观测等空间光学任务中发挥着越来越重要的作用[2]。其典型的应用为航天器星体与FSM构成粗精分层的两级光束稳定与控制系统，使大范围快速跟踪与高精度指向相结合[3]。其中FSM是光学载荷中光束稳定与高精度指向控制的重要组成部分，因此分析FSM的指向控制精度，对FSM及其控制系统各部分进行优化设计，对提高FSM控制系统的指向控制精度以及光束稳定性具有重要意义。

在航天器星体与FSM构成粗精分层的两级系统中影响快反镜指向控制精度的因素主要包括星体指向误差、星体角速度误差、FSM姿态测量误差、FSM执行机构输出力矩误差。目前，甚高精度航天器的姿态控制精度<0.01°，稳定度优于1×10-3(°/s)[4]。导星敏感器是实现快反镜高精度控制的重要姿态测量设备。加拿大航天局研制的导星敏感器能够实现优于5 mas的高精度姿态测量[5]。快反镜基座安装在航天器载荷中，即航天器的姿态控制误差和角速度误差通过柔性铰链和驱动器[6]直接影响快反镜基座的稳定性，进而影响快反镜指向控制精度。快反镜的姿态指向控制精度与其动力学模型息息相关。Hei[7]等建立了带有柔性支承结构的FSM动力学模型，模型中考虑了轴间耦合以及执行机构的高频谐振等影响因素，为分析快反镜指向控制精度提供了一种参考模型。Long[8]等提出了一种提高望远镜指向精度的新模型，说明了制造和装配过程中不精确所造成的几何误差及其对望远镜指向精度的影响，为快反镜指向误差分析提供了依据。Zhu[9]等建立了压电结构驱动的快反镜动力学模型，其动力学模型为5阶模型，针对此模型采用混合控制器能够实现快反镜指向精度优于0.008 mrad。该指向精度中没有综合考虑FSM基座的扰动和执行机构的输出力精度等影响因素。

针对快反镜指向控制精度分析中存在的问题，本文提出了一种指向控制误差分析方法，分析了4种对FSM控制系统精度产生影响的扰动及其影响力度，为提高快反镜的指向控制精度提供指导，对快反镜的设计与制造具有实际意义。本文建立了带有高阶谐振的FSM动力学模型，采用PID整定规则设计了FSM控制系统的控制器，使FSM控制系统在无外界扰动时满足其指向控制性能指标。在此基础上推导了星体指向误差、星体角速度误差、快反镜执行机构输出力矩误差、快反镜姿态测量误差共4种影响因素至FSM指向的闭环系统传递函数。基于FSM控制系统，研究了上述4种影响因素对FSM控制精度产生影响的程度，并给出了其对FSM指向控制误差的定量分析结果，为改善快速反射镜的指向控制精度提供针对性指导。

1 FSM控制系统建模

目前，FSM的机械结构主要有单轴两驱动、两轴两驱动、两轴三驱动和两轴四驱动4种。为简化分析，本文考虑一种简单情况：单轴两驱动结构的FSM指向控制系统。

1.1 FSM系统理想模型

单轴FSM系统理想模型如图1所示。

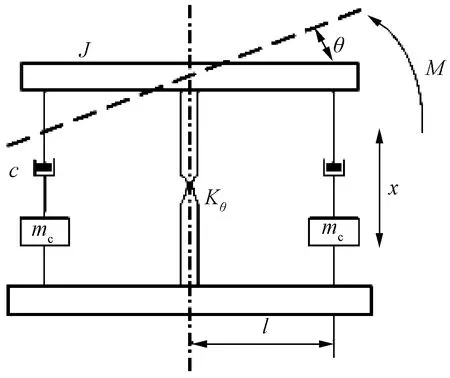
图1 FSM单轴理想模型

快反镜控制系统中包括反射镜、柔性支承结构、执行机构(本文以音圈电机为例)和基座等部分[10-11]。当考虑快反镜基座固定不动时，快反镜指向控制系统等效为二级系统模型，其力矩平衡方程式可表示为[1]

(1)

式中：M为快反镜控制力矩；J为反射镜和柔性支承结构的等效惯量；θ为反射镜输出姿态角；Kθ为柔性支承轴向扭转刚度；c为柔性支承与音圈电机的等效阻尼系数；mc为音圈电机动子质量；l为音圈电机力作用点到反射镜转轴的距离。

由此得到快反镜输出角度与输入力矩之间的传递函数为

(2)

快反镜姿态与其执行机构音圈电机行程之间的运动学关系满足：

(3)

式中x1、x2为2个音圈电机的轴向平动位移，可通过位移敏感器测量。

进一步对2个音圈电机进行建模，最终得到单轴FSM系统理想模型下的传递函数为

(4)

式中：U为音圈电机输入电压；Kf为电机力矩系数；R为电机线圈内阻；L为电机线圈电感；Ke为电机反电动势系数。

1.2 带有高阶谐振的单轴FSM模型

实际的FSM较理想模型复杂得多，通常存在多个谐振频率[12]，如图2所示。为了准确描述FSM的幅频特性，需对FSM的高阶谐振进一步建模。

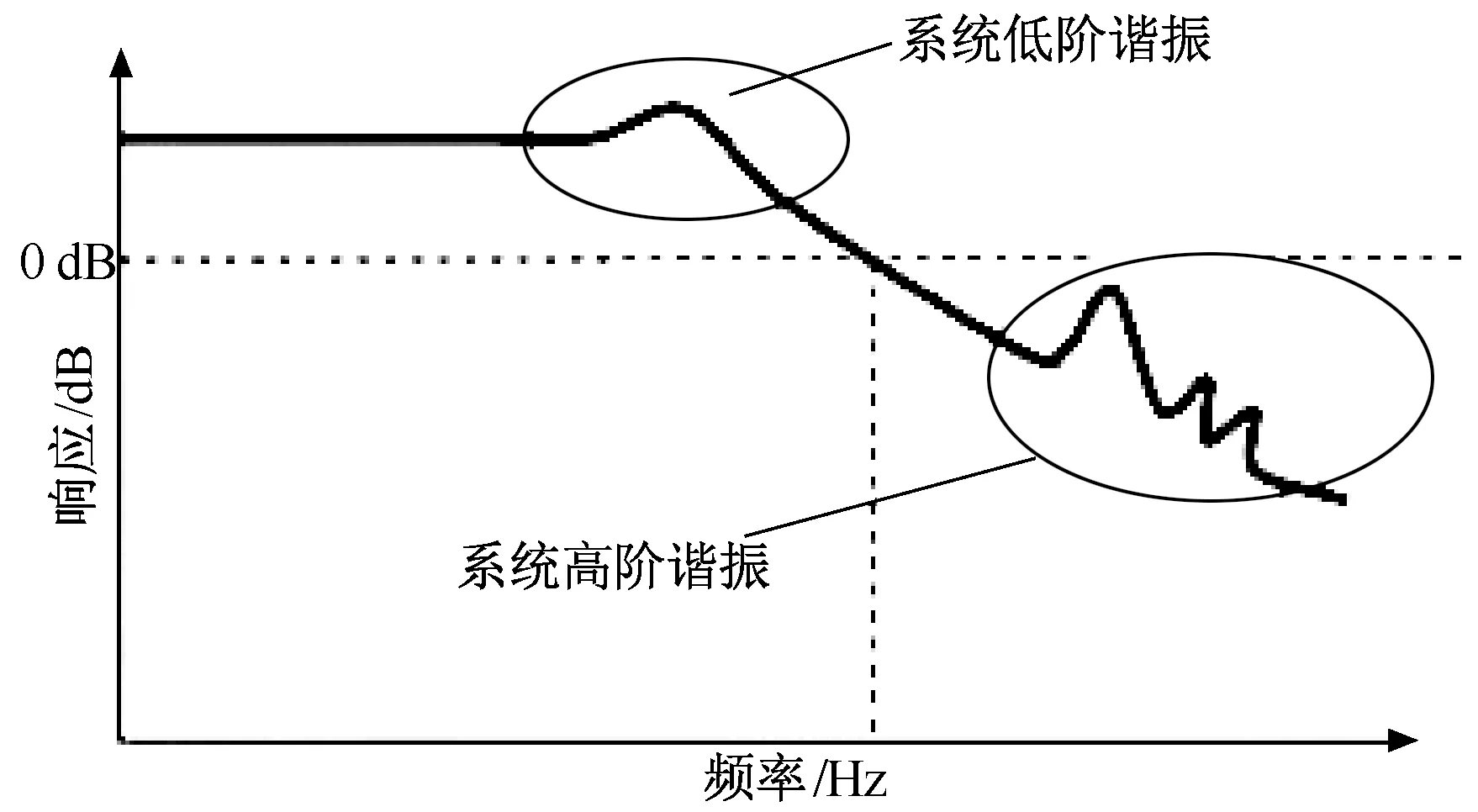
图2 FSM频域特性示意图

对于本文所述的FSM结构，由于其自由度方向刚度远低于非自由度方向刚度，因而其低阶谐振主要由自由度方向刚度决定；另外，由于加工装配精度、寄生效应等因素，FSM高阶谐振主要由非自由度方向对自由度方向的运动耦合造成。对于系统高阶谐振，由FSM的有限元模型可知，限制FSM带宽提高的高阶谐振振型主要为绕柔性支承所在轴的转动和沿柔性支承所在轴的拉伸[3]。由于FSM非自由度方向对自由度方向的耦合运动受较多非线性及不确定因素的影响，使得高阶谐振成因较为复杂，难于准确建立其定量理论模型。因为FSM运动范围较小，为简化分析，将该耦合简化为一个线性增益系数K△。参照1.1节中方法，令KθZ为柔性支承所在轴的扭转刚度，Kz为柔性支承所在轴的拉伸刚度，K△为柔性支承所在轴的扭转和拉伸在自由度方向上的耦合增益系数，则可得到系统带有高阶谐振的模型，如图3所示。

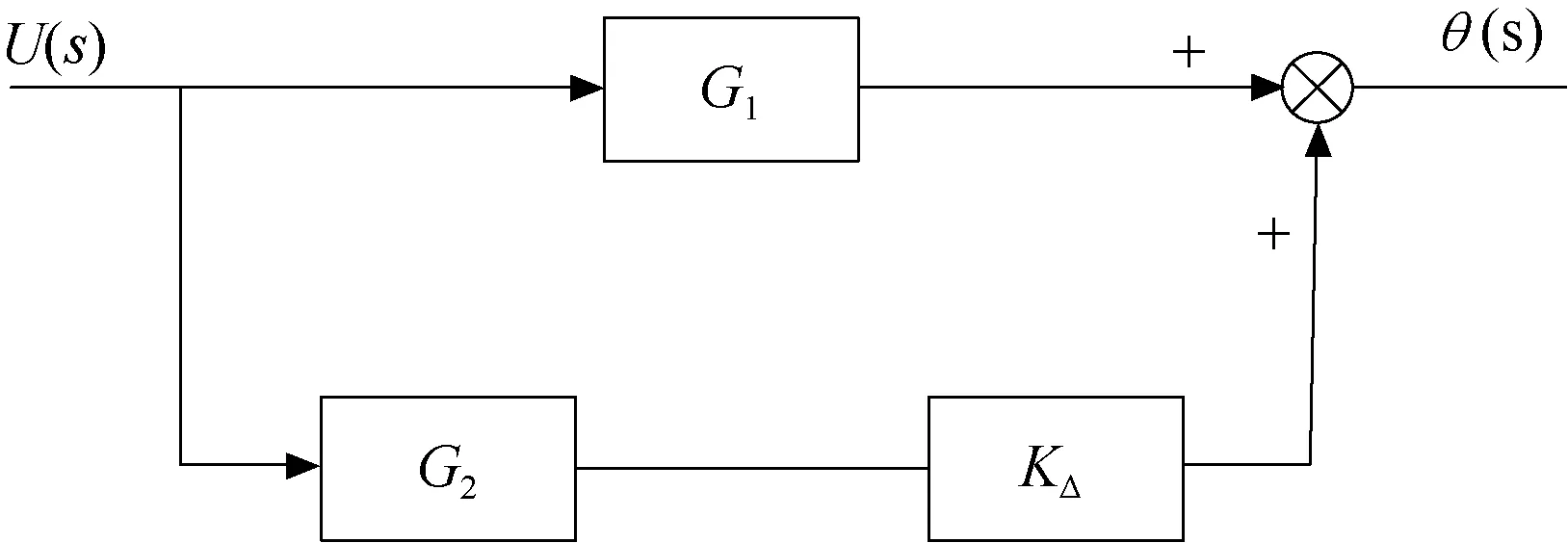
图3 加入高阶谐振的FSM模型

图3中，G1(s)如式(4)所示，G2(s)如式(5)所示，采用文献[1]中的测试结果，K△取0.1。

(5)

式中：JZ为柔性支承所在轴的转动惯量；mZ为柔性支承的质量。

1.3 单轴FSM控制系统

根据以上分析，可以得到带有高阶谐振的FSM系统的传递函数：

(6)

以表1中某型FSM指标要求为例，进行FSM控制器的设计。

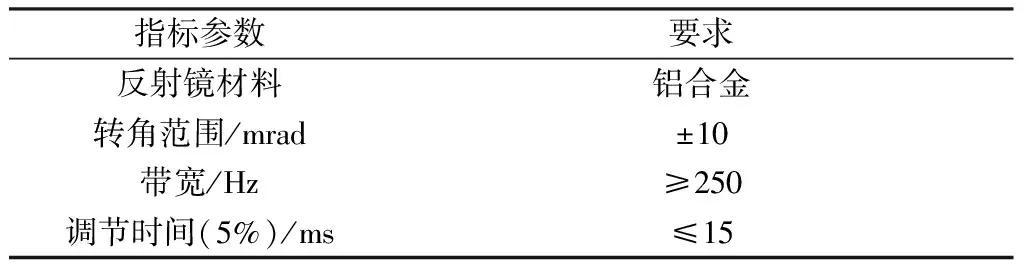
表1 某型FSM性能指标

采用PID整定规则，利用SISOTOOL设计工具，最终得到符合性能指标要求的闭环控制器C(s)：

(7)

根据以上分析，可以得到无扰动时带有高阶谐振的单轴FSM控制系统，如图4所示。

图4 无扰动时的单轴FSM控制系统

图中，θup为反射镜的目标姿态角；Vca为对音圈电机建模后得到的传递函数，其表达式为[13-14]

(8)

此系统的闭环传递函数为

G(s)=

(9)

2 影响因素分析

上述所有分析均是基于系统无外界扰动的情况。实际环境中，在FSM的工作过程中总是存在各种扰动。因此在进行FSM控制系统设计时要对各种可能存在的扰动进行分析，并在设计过程中尽量减小或补偿扰动带来的影响以实现期望目标。本文根据FSM的实际工作环境及工作过程，分析了系统中存在的4种扰动，并设计了带有扰动的单轴FSM闭环控制系统，如图5所示。

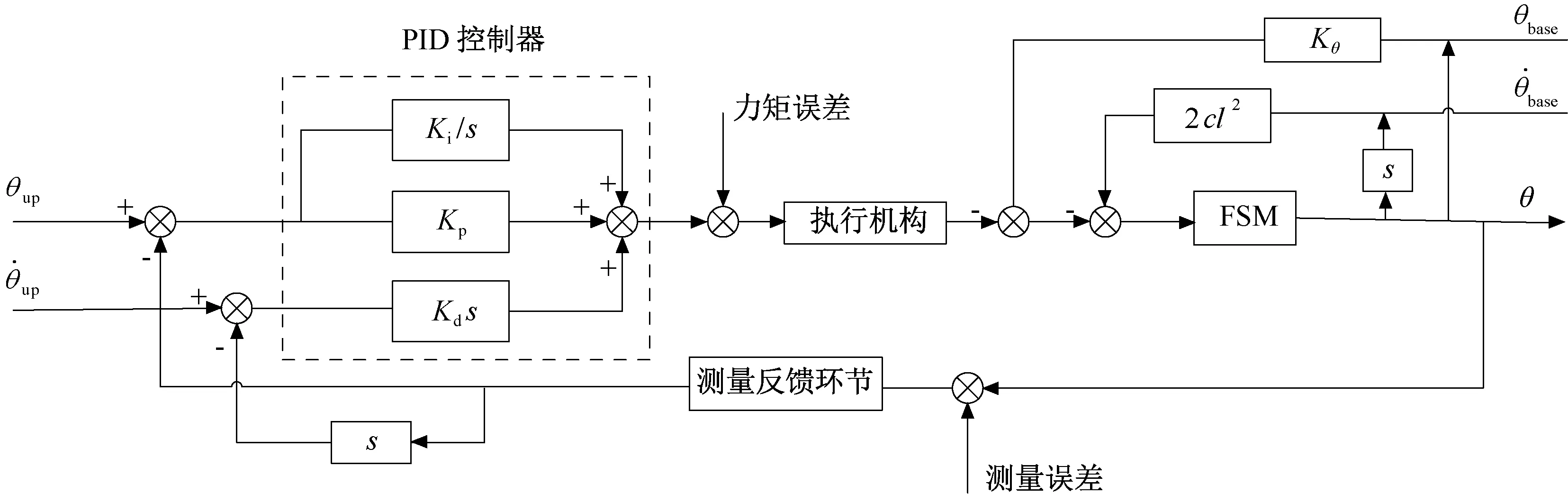
图5 带有高阶谐振的单轴FSM控制系统

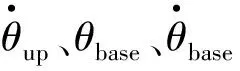
2.1 执行机构力矩误差

FSM的执行机构(本文以音圈电机[14]为例)在工作过程中会受到摩擦、噪声力矩等因素的影响，从而影响FSM反射镜的输出角度和角速度，进而影响FSM的指向精度。以FSM执行机构力矩误差作为输入时的FSM控制系统传递函数为

(10)

式中D(s)为快反镜执行机构力矩误差。其表达式为[15]

D(s)=[3×10-6×sin(2πt)](N·m)

(11)

此时的系统输出为

θ1(s)=D(s)Gdis(s)

(12)

2.2 姿态测量误差

单轴FSM控制系统是一个闭环负反馈控制系统。以传感器为核心器件的姿态测量环节是此系统的重要组成部分，姿态测量误差直接影响整个FSM控制系统的指向控制精度。传感器的测量精度会受制造工艺等的影响，在测量过程中也会不可避免地引入测量噪声。以姿态测量误差作为输入时的FSM控制系统传递函数为

(13)

式中：N(s)为姿态测量误差。其表达式为[16]

N(s)=[0.005×sin(2πt)](″)

(14)

此时的系统输出为

θ2(s)=N(s)·Gnoise(s)

(15)

2.3 星体指向误差

基座作为FSM机械结构中的重要组成部分，是整个FSM保持稳定的前提。航天器星体与快反镜基座相连。航天器星体指向误差直接影响快反镜基座的姿态误差和稳定度。当基座受外界干扰产生振动时，其振动的角度会通过柔性支承传递至反射镜，进而影响FSM的指向精度。以星体指向误差为输入时的FSM控制系统传递函数为

(16)

式中θbase(s)为星体指向误差角。其表达式为[15]

θbase(s)=[1×sin(2πt)](″)

(17)

此时的系统输出为

θ3(s)=θbase(s)Gbase-θ(s)

(18)

2.4 星体角速度误差

当基座受外界干扰不稳定时，其振动的角速度会通过音圈电机传递至快反镜，进而影响FSM的执行精度。以星体角速度误差为输入时的FSM控制系统传递函数为

(19)

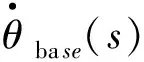
(20)

此时的系统输出为

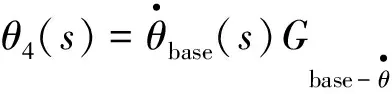
(21)

3 仿真验证与分析

以某型FSM为例设计仿真实验，性能参数如表2所示。

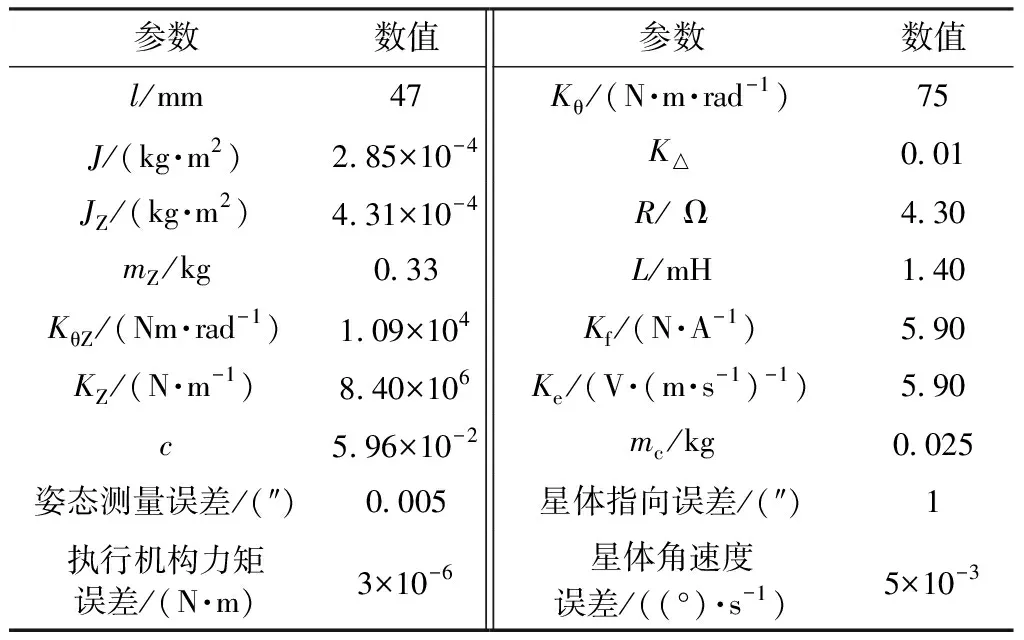
表2 某型FSM性能参数

利用表2中所列参数对图4所示系统进行性能仿真，并使用SISOTOOL对系统控制器进行设计，得到系统的闭环Bode图和闭环阶跃响应如图6、图7所示。可以看出，本文所述FSM模型是正确可靠的，可在此基础上作进一步的分析研究。

图6 FSM模型闭环Bode图

图7 FSM模型闭环阶跃响应

以表2中所列的姿态测量误差、执行机构力矩误差、星体指向误差、星体角速度误差为输入，对快反镜闭环控制系统指向控制误差进行仿真，结果如图8所示。仿真结果显示，在4种扰动同时存在的情况下，FSM指向总误差优于10 mas。此结果优于文献[14]中给出的快反镜指向精度(1.17″)，这是因为本文中均采用最新的研究数据进行仿真分析。单个误差源分析结果：FSM姿态测量误差引起的指向误差为5 mas，FSM执行机构力矩误差引起的指向误差为2.4 mas，星体指向姿态误差引起的指向误差为5.9 mas，星体角速度误差引起的指向误差为0.21 mas。

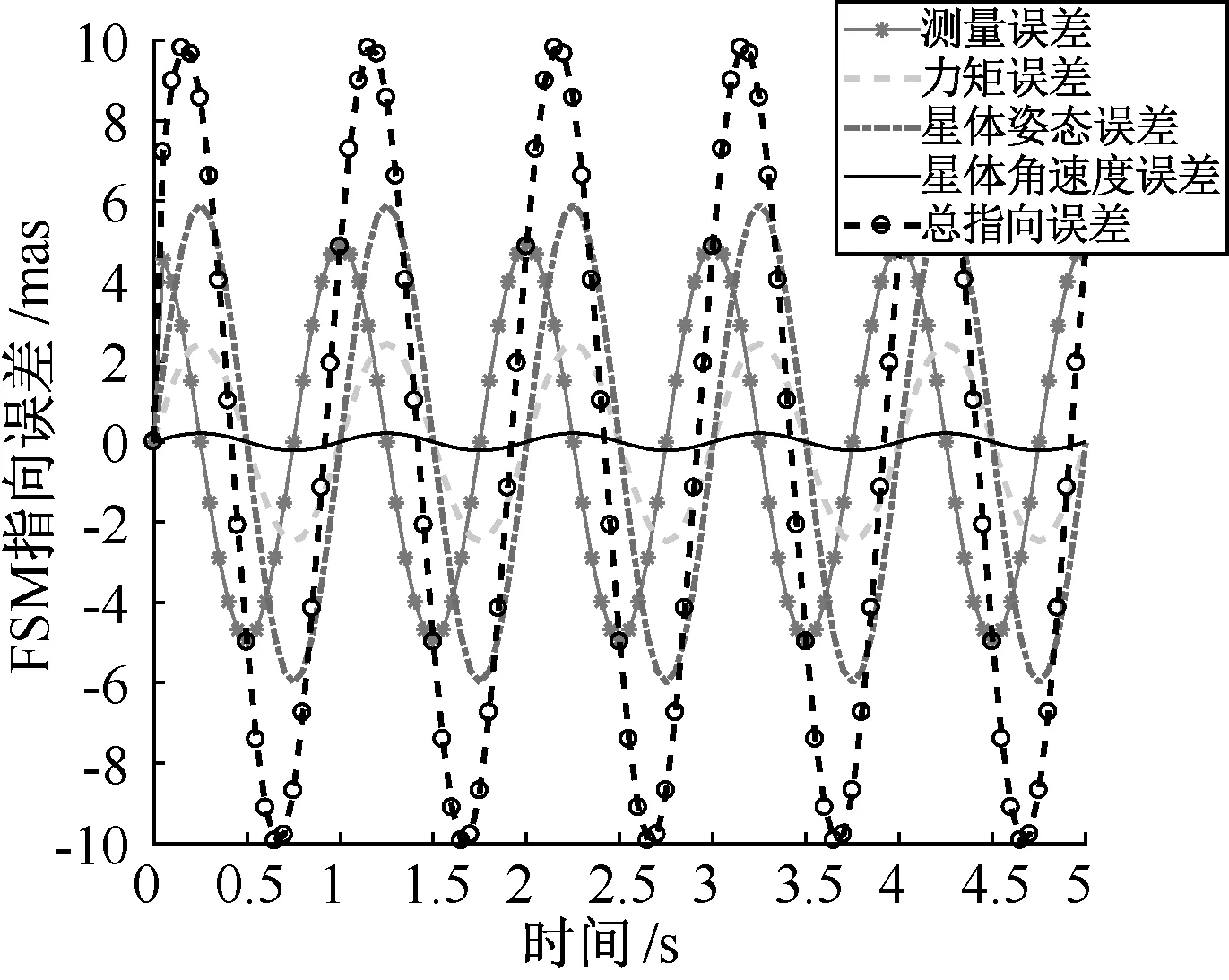
图8 各误差源同时存在时快反镜的指向误差

各误差源对快反镜指向误差的影响如图9所示，从图中可以看出，星体姿态误差占快反镜指向总误差的53.1%，FSM姿态测量误差占快反镜指向总误差的38.1%，是导致快反镜指向误差的主要原因。

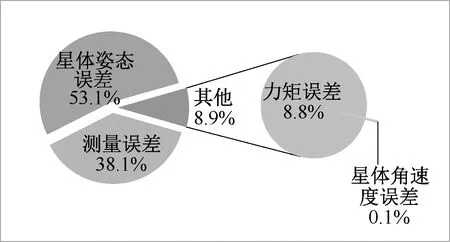
图9 各误差源对快反镜指向控制精度影响占比

4 结束语

本文针对FSM控制系统的指向控制精度问题，提出了一种快反镜闭环控制系统指向控制误差分析方法，并利用此方法进行仿真,验证了该方法的可行性和有效性。利用该分析方法对快反镜指向控制误差进行分析可知，进行快反镜及其控制系统设计时，应该首先降低星体姿态误差和FSM姿态测量误差，以进一步提升快反镜指向性能，从而提高航天器星体和快反镜两级系统的指向控制精度。

本文基于单轴两驱动的快反镜动力学模型对快反镜的指向控制误差进行了分析，在对音圈电机的建模过程中进行了一定的简化分析，音圈电机的实际工作过程中需建立更复杂的模型，这可作为下一步的研究方向。单轴快反镜是一种较为简单的情形。工程实际中，快反镜的结构主要有单轴、双轴两种，其中双轴快反镜还需要考虑轴间耦合等因素引起的快反镜指向控制误差，这可作为下一步的研究方向。