基于T-S模糊神经网络自动换挡策略研究

张小虎，王立勇，唐长亮

(1.北京信息科技大学 机电工程学院，北京 100192；2.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192)

0 引言

车辆自动变速器的关键技术是我国车辆发展的重要因素。车辆的动力性、经济性以及乘坐的舒适性不仅取决于发动机的优劣，而且与变速器的性能也有很大的关系[1-3]。目前自动变速器主要分为5类：液力机械式自动变速器(AT)、无极变速器(CVT)、双离合式自动变速器(DCT)、无级变速机械式自动变速器(IVT)和电控机械式自动变速器(AMT)。AT是由液力变矩器和变速器组合而成，液力变矩器的应用减小了换挡过程震动，提高了车辆的乘坐舒适性[4]；CVT变速比是连续值，有良好的经济性与平顺性；DCT具有2个离合器，在换挡过程中，一个离合器断开，另一个离合器啮合，2个离合器依次使用，没有动力间断现象；IVT是由变速器和行星排构成，可以承受大的载荷；AMT是对传统手动变速器加以改进，加上自动变速系统，具有传动效率高、结构紧凑、成本低等优点。

对自动换挡的研究主要集中在控制策略上。赵丁选等[5]对传统的BP神经网络进行了改进，改善了传统算法收敛速度慢等缺点；李平康等[6]将基于模糊规则递推调整算法应用在车辆自动换挡上，提高了车辆的动力性；易军等[7]采用参数自调整模糊控制方法，对不确定的车辆参数和外部负载扰动具有很好的鲁棒性；陈清洪等[8]提出了动态模糊神经网络算法，与两参数相比三参数输入鲁棒性更强。有些学者也对一些特殊工况下的控制策略进行了研究，例如下坡时换挡策略的研究[9]。但是，国内对自动换挡策略的研究，比较常用的控制算法主要有神经网络算法和模糊算法，集成两者优点的换挡策略研究较少。将T-S模糊神经网络应用到自动换挡上，结合了模糊算法与神经网络算法，模型可用少量的模糊规则生成较复杂的非线性函数，对于自动换挡研究具有一定的应用价值和指导意义。

1 T-S模糊神经网络换挡原理

T-S模糊神经网络自动换挡原理如图1所示。首先采集车辆在不同的油门开度以及行驶车速下对应的档位值，将采集的车速、油门开度以及对应的档位作为训练样本，用提取的样本对训练模型进行训练，将训练好的模型放到换挡控制器中，当油门开度和车速信号输入到训练好的T-S模糊神经网络中，经过模糊神经网络算法，输出档位信号，档位信号驱动变速器换挡。

图1 T-S模糊神经网络自动换挡原理

2 建立T-S模糊神经网络模型

神经网络算法具有并行计算、分布式信息存储以及自学习等一系列优点，类似于人脑的学习、记忆和分析等功能；模糊控制算法模拟人脑的思维方式，以模糊推理的方式处理日常难以解决的问题。模糊控制算法主要是从宏观出发，研究模糊性的问题；神经网络主要从微观出发，模拟神经元的工作方式。T-S模糊神经网络继承了两者的优点，并成为处理非线性系统的有力工具[10-12]。

目前有2种模糊神经网络应用最为广泛，这2种模糊神经网络的区别是基于2种不同的模糊推理，一种是基于标准模型(Mamdani)的模糊神经网络，另外一种是基于T-S模型的模糊神经网络。2种模糊推理各有优缺点：Mamdani模糊推理输出量仍然是模糊量，更加符合人类的思维方式和语言表达习惯；T-S模糊推理输出是输入变量的线型组合。与Mamdani模糊推理相比，T-S模糊推理不仅效率高，而且能够更好地与线型理论配合，适合数学分析[13-14]。

2.1 T-S模糊神经网络结构

如图2所示，T-S模糊神经网络主要分为前件网络和后件网络,均有4层节点。前件网络A、C层有2个节点，B层有4个节点，D层有1个输出节点；后件网络 A、B和C层均有2个节点，D层有1个输出节点。

图2 T-S模糊神经网络结构

前件网络的A层为油门开度a和车速v的归一化结果，B层为模糊层，隶属度函数采用高斯函数。

(1)

前件网络C层输出为

(2)

前件网络D层输出为

(3)

后件网络的A层输出同样为油门开度a和车速v的归一化结果。

B层输出为

(4)

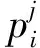
C层输出为

(5)

D层输出为

(6)

模糊神经网络的最终输出为反归一化结果：

(7)

2.2 学习与训练算法

T-S模糊神经网络学习与训练算法原理如图3所示。用提取的样本对模型进行训练，训练后输出实际档位，实际档位与目标档位对比，如果误差在允许范围内，则训练结束，否则就用最速下降法进行搜索，反向计算出隶属度函数参数以及权值，重复前面工作。

图3 学习与训练算法原理

实际输出与目标输出的误差函数定义为

(8)

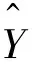
为了使输出逼近输出，需要使E的值最小，采用最速下降法进行搜索，搜索方法可以由式(9)表示：

(9)

从而可以得到3个参数的表达式为：

(10)

(11)

(12)

式中：α为学习速率；θ为动量因子。

3 仿真与结果

3.1 仿真过程

3.1.1 数据采集

AT自动变速器的换挡控制策略的制定主要有2种方法，一种是根据车辆相邻挡位驱动力曲线计算出换挡点，另一种方法是根据优秀驾驶员的驾驶习惯制定换挡曲线。

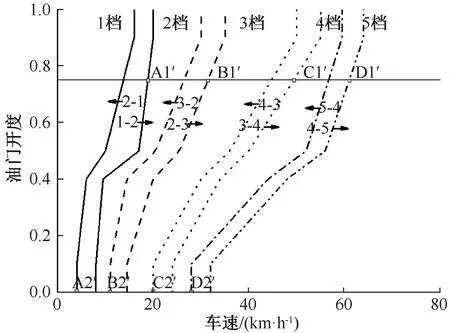
图4为某一款车辆换挡曲线图。在换挡曲线图中均匀提取15 200个数据点，用这些数据点模拟优秀驾驶员的驾驶习，将这些数据作为训练样本。

图4 换挡曲线图

换挡曲线一共5个档位，每个档位之间有交叉部分，这样就避免车辆在换挡点附近行驶时引起频繁换挡现象，一方面延长了变速器的使用寿命，另一方面增加了车辆的稳定性以及乘坐的舒适性。

在训练时把1档和2档之间的重叠区域定义为1.5档，同样2档和3档之间、3档和4档之间以及4档和5档之间的重叠区域分别定义为2.5档、3.5档以及4.5档。

3.1.2 训练模型

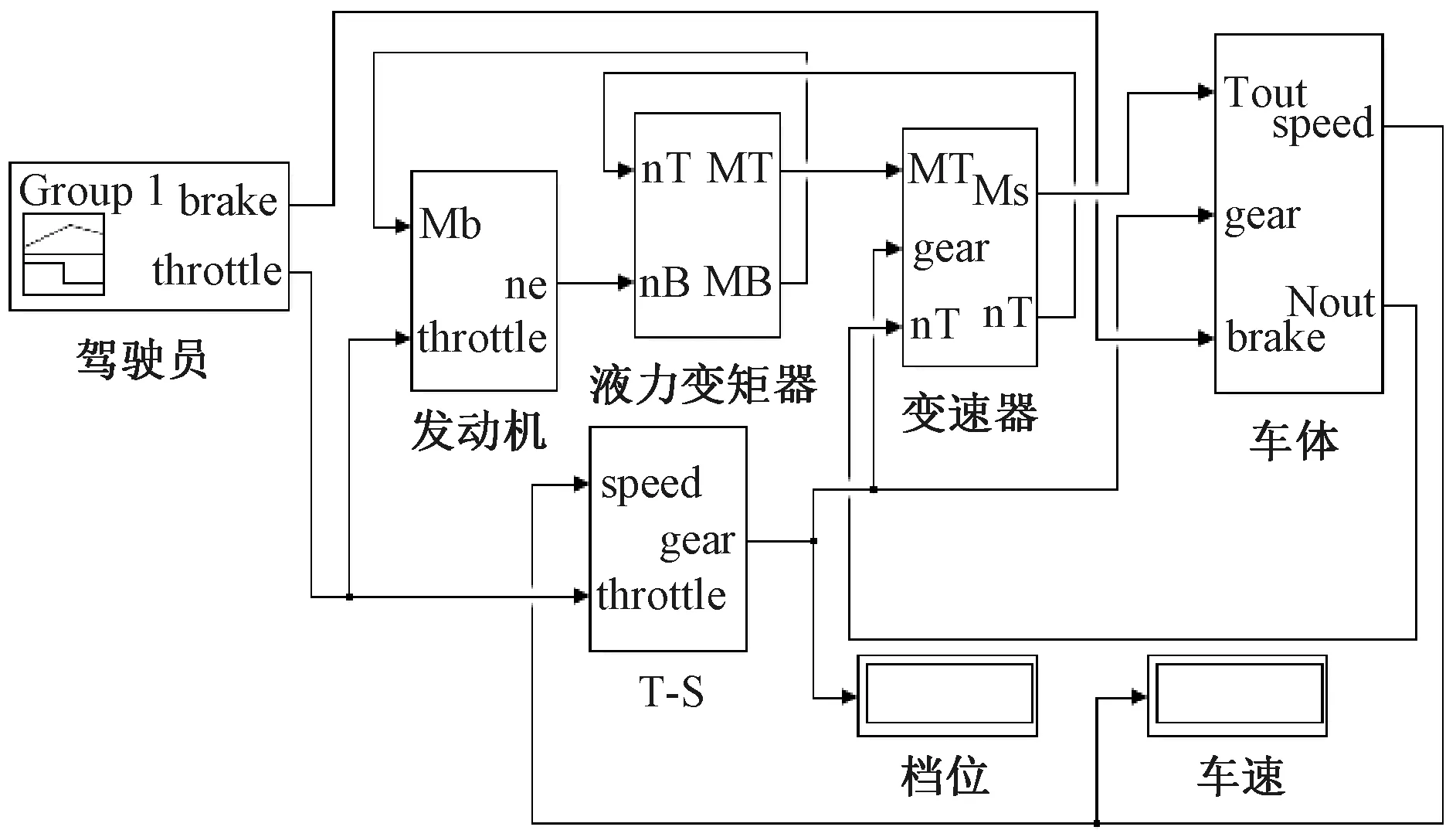
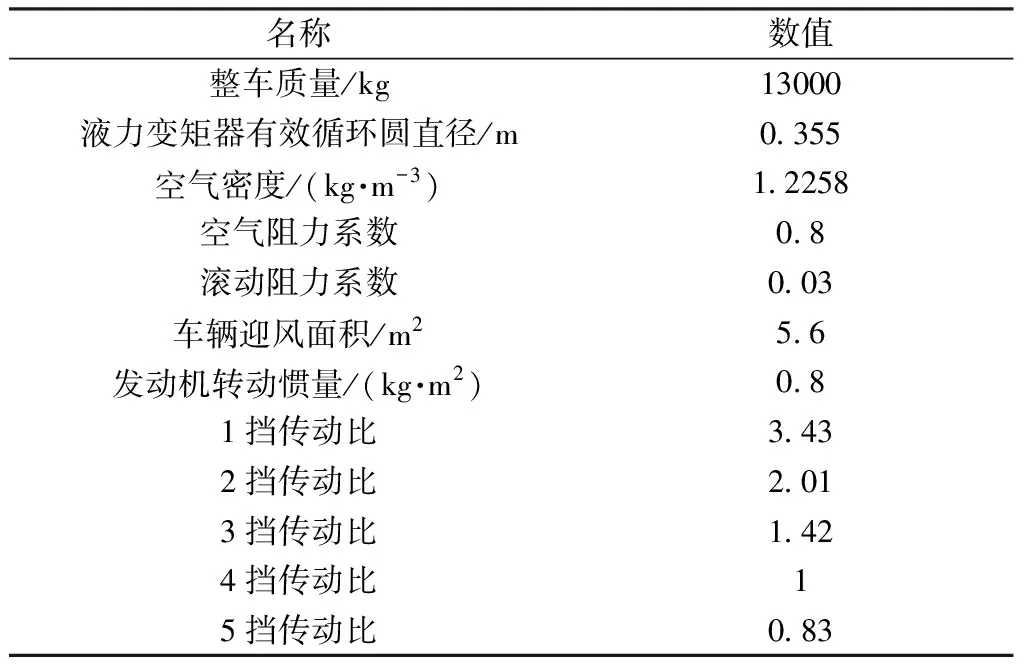
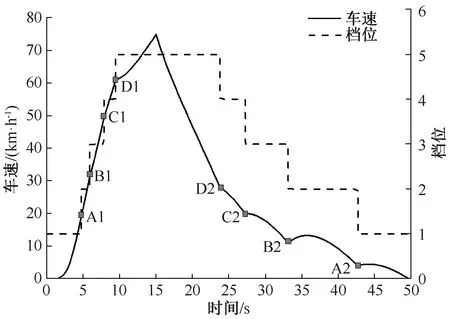
把采集到的数据点输入到控制算法中，训练出c、σ以及p三个参数的数值，同时也会得到训练后的实际档位值以及训练误差，如图5所示。训练过程中会有一定的误差，最大误差在10%以内。因为模型中有取整过程(比如当训练后的档位为n，当1.75

图5 实际输出与训练误差

3.1.3 搭建仿真模型

表2 理想、实际的档位与车速

仿真系统总体结构主要包括发动机模型、液力变矩器模型、变速器模型、车体模型以及控制算法模型。根据车辆关键部分的模型公式，在matlab/simulink中搭建仿真模型，如图6所示。

图6 matlab/simulink仿真模型

仿真所用参数如表1所示。

3.2 仿真结果

仿真过程有2个阶段：油门开度为70%时车辆加速过程；加速15 s后油门开度为0，刹车减速过程。图7是油门开度为0以及70%时理想换挡点，图8为实际的档位与车速曲线图。

表1 仿真参数设定

图7 理想换挡点

图8 实际速度与档位曲线图

通过对比图7与图8，整理出实际情况下以及理想情况下对应的车速和档位，如表2所示。从表2可以看出，在换挡点处实际车速和理想车速误差在2%以内，证明了运用的算法的可行性。

4 结束语

为了提高车辆的动力性以及乘坐的舒适性，本文将T-S模糊神经网络应用于自动换挡中。在matlab/simulink搭建仿真模型，在先加速后减速的工况下进行仿真，仿真结果表明换挡点误差在2%以内，满足换挡要求，证明了运用算法的可行性以及较强的鲁棒性。