右转机动车与非机动车冲突博弈行为分析
张翠平,于瑞康,赵 晖
(1.北京信息科技大学 计算机学院,北京 100192;2.山东高速物流集团有限公司 安全管理部,济南 250098;3.北京交通大学 交通运输学院,北京 100044)
0 引言
作为改善路段安全性的重要手段,城市道路交通安全评价逐渐成为人们关注的热点。城市道路网络中的节点,信号交叉口是城市道路网络通行能力的关键所在。各方向车流之间的冲突错综复杂,使得交叉口成为城市交通事故的多发地带。其中,右转机动车与相邻车道直行非机动车有明显冲突,它们在进入冲突点时会有博弈行为出现。因而,可以采用博弈论的思想来研究机动车与非机动车的冲突决策行为。
交通冲突是不安全交通行为的外在表现形式,与交通拥堵、交通事故风险高度关联[1]。参与人、策略和收益是博弈论综合考虑的3个必备因素,是从收益和结果来综合分析和衡量参与人冲突及内在风险的科学。由于城市交通环境复杂,无法直观对其进行较全面的认识。交通参与人之间的冲突可以采用博弈论方法进行分析。Mesterton-Gibbons[2]通过研究交叉口处的机动车博弈行为,将问题建模为对称非合作博弈,得到了混合策略的最优解。Arslanyilmaz等[3]基于博弈的多用户在线驾驶训练系统,研究了新手驾驶员的危险感知能力特征。Feldmann[4]研究了具有自利性的出行者在共享网络中的出行行为,假设用户通过极小化其潜在利益来选择其出行路径,并与其它交通参与者进行博弈,则有稳定的纳什均衡点存在。Liu等[5]以我国无信号交叉口驾驶员的风险感知为研究对象,结合风险感知对无信号交叉口驾驶员的博弈交互行为进行了分析。邵祖峰[6]建立了交通管理方和交通参与者的博弈模型,研究表明两者的博弈是一个混合战略均衡,且管理方的检查行为与参与方的违章行为具有概率意义上的依存性。董甜甜等[7]对政府和出行者2个博弈主体进行分析,利用博弈论方法从政府角度对出行者的出行行为选择进行研究,通过运用混合战略模型中的效用函数公式综合分析政府和出行者的期望效用,探讨政府用来缓解交通拥堵的经济政策。牟秋[8]对普遍存在的交叉口左转机动车强制变道行为,运用博弈论思想从变道特性、变道模型、变道延误、变道安全及管理策略等方面展开研究,并提出了对危险变道行为的监控与处罚方法。
国内外学者主要针对机动车和行人交通冲突进行了研究,而很少针对机动车与非机动车的冲突进行分析。本文针对交叉口右转机动车与非机动车的冲突行为,采用博弈论的方法展开研究。
1 冲突决策分析
右转机动车一般不受信号灯控制,其与相对灵活的非机动车在接近交叉口的时候会发生博弈行为,博弈双方的决策会对冲突的严重性产生影响。当右转机动车与非机动车到达交叉口时,两类局中人开始博弈。右转机动车与非机动车在通过冲突区域的过程中,若机动车或非机动车未改变原有运动状态且未发生冲突,则此时双方的收益均为0;若机动车或非机动车通过冲突区域时需要等待,或发生了交通冲突,则此时收益为负。因此,机动车和非机动车的收益主要包括延误和冲突风险2个部分。对于延误带来的收益,设机动车的延误损失为d1 d,非机动车的延误损失为d2 d;对于冲突带来的收益,设机动车因发生冲突产生的风险损失为d1c,且d1 d远小于d1c,对于任一严重等级的冲突,其发生概率值用Pc表示,那么对于机动车,其冲突损失的期望可以表示为Pc·d1c。同样地,设非机动车发生冲突产生的风险损失为d2c,且d2 d远小于d2c,则非机动车承担冲突发生后的损失期望为Pc·d2c。
根据冲突特征,对于机动车与非机动车手双方必须考虑采取不同决策时的延误和风险方法,机动车决策行为的收益函数为:
抢行决策:
d1=Pc·d1c
(1)
等待决策:
d1=Pc(d1c+d1 d)
(2)
非机动车决策行为收益函数为:
抢行决策:
d2=Pc·d2c
(3)
等待决策:
d2=Pc(d2c+d2 d)
(4)
经过实地考察,本文作者选取车公庄大街-车公庄南街信号交叉口进行交通实测。根据观测数据,计算得到机动车与非机动车的决策冲突概率Pc如表1所示。

表1 不同决策行为对应的不同等级冲突风险概率 %
一般情况下,无论是机动车还是非机动车,速度越快,其通过交叉口的时间就越短,延误损失也就越小。因而当发生的冲突严重程度较高时,对于机动车而言,其延误损失d2 d比非机动车的延误损失d1 d小得多;而另一方面,无论是机动车还是非机动车,其速度越快,其安全风险越高,损失越大。当发生的冲突严重程度较高时,非机动车的风险损失d1c远小于机动车风险损失d2c。机动车和非机动车不同冲突风险等级下的风险与损失如表2所示。一般情况下,冲突风险损失值取值区间为[-9,-1],损失值越小则冲突发生的风险越大。

表2 机动车与非机动车冲突风险损失值
根据机动车与非机动车的决策行为收益函数,可计算出机动车与非机动车的决策行为收益值,如表3所示。

表3 机动车驾驶员决策行为收益值
2 基于非合作动态博弈的决策模型
构建完整的冲突博弈模型需要对参与人及其策略进行分析。根据机动车与非机动车冲突的时空规律,其博弈过程可看作是一个序贯博弈。
设机动车的策略集为{抢行,等待},用{C1,W1}来表示;非机动车的策略集同样为{抢行,等待},用{C2,W2}来表示。一般来说,可以将这个序贯博弈从机动车首先决策和非机动车首先决策2个方面进行分析。
假设机动车首先决策,在博弈开始时,机动车就会首先对可能发生的冲突进行预判,设其概率为P1、P2、P3,然后根据收益值进行决策,此时机动车的策略为C1、W1,紧接着非机动车根据机动车的决策状态进行决策,其策略为C2、W2。
在第一阶段,机动车的策略集可表示为{C1C1C1,C1C1W1,C1W1C1,C1W1W1,W1C1C1,W1C1W1,W1W1C1,W1W1W1},用来描述机动车在第一层信息节点上采取的策略。在第二阶段,非机动车的策略集合可表示为{C2C2,C2W2,W2C2,W2W2},用来描述非机动车在第二层信息节点上采取的策略。通过上述分析,可得到双方的效用支付为d1(Pk;(s1,s2)),d2(Pk;(s1,s2)),如图1所示。

图1 机动车驾驶员首先决策情况下的博弈展开式
假设在博弈过程中,非机动车首先做出决策,且有C2、W2两种策略,机动车有C1、W1两种策略可以选择。
在第一阶段,非机动车的决策集合可表示为{C2C2C2,C2C2W2,C2W2C2,C2W2W2,W2C2C2,W2C2W2,W2W2C2,W2W2W2},用来描述机动车在第一层信息节点上采取的策略。在第二阶段,机动车的策略集合可表示为{C1C1,C1W1,W1C1,W1W1},用来描述机动车在第二层信息节点上采取的策略。通过上述分析,可得到局中人双方在博弈过程中的支付效用d1(Pk;(s2,s1)),d2(Pk;(s2,s1)),如图2所示。

图2 非机动车首先决策情况下的博弈展开式
根据2种情况下的博弈展开式,能够构建机动车与非机动车的收益矩阵。
当机动车首先决策时,如果机动车和非机动车都采取抢行策略,势必增加发生严重冲突的可能性,非机动车在这个博弈过程中承担了巨大的风险;反之,如果机动车和非机动车都采取等待的策略,则会同时减小冲突风险,增加等待时间,出现冲突风险与延误相互抵消的结果。因此,可以重新博弈双方局中人各自的收益值,如表4所示。
当非机动车首先决策时,如果机动车和非机动车都采取抢行策略,则发生严重冲突的概率必然增大,此时,非机动车将承担更高的风险;反之,如果机动车和非机动车无论何方首先决策,都采取等待策略,则必然会降低冲突风险。但与此同时,由于机动车非机动车均增加了等待时间,故可能发生风险与延误相互抵消的情况。冲突风险与博弈局中人双方的收益值如表5所示。

表4 机动车驾驶员首先决策的收益
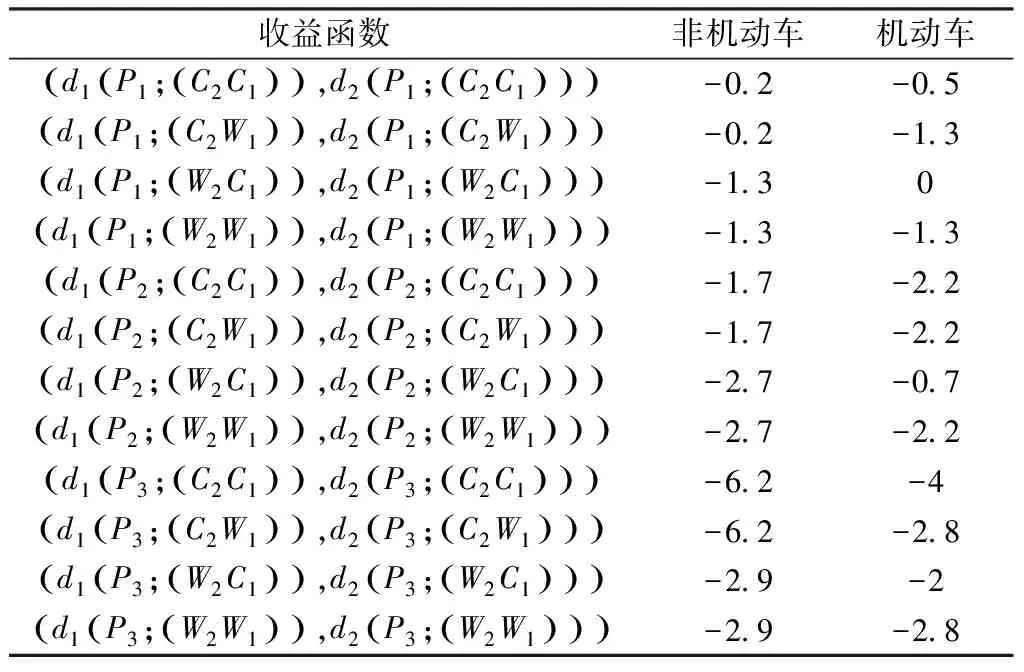
表5 非机动车首先决策的收益
已知机动车和非机动车其中一方首先决策时的博弈展开式及决策收益,就可以构建基于动态非合作博弈的机动车和非机动车的冲突决策模型。
当机动车首先决策,根据表2得到的收益矩阵得到博弈展开式如图3所示。
当观察到机动车首先进行决策时,由于机动车速度较快,非机动车无法预判冲突的严重程度。对于机动车来讲,在第一层信息节点上,在发生中等冲突和轻微冲突的情况下采取抢行(C1)都将是其最优策略;对非机动车来讲,机动车首先决策且优先选择抢行(C1),那么在第二层信息节点上,其选择等待(W2)都是最好选择。

图3 机动车驾驶员首先决策情况下的博弈展开式
根据以上分析,能够计算出均衡解的收益,根据调查数据标定的风险等级概率值P1、P2和P3分别为:
P1=0.40,P2=0.34,P=0.26
(5)
因此,机动车和非机动车的期望收益(EX1,EX2)为:
EX1=P1·d1(P1;(C1,W2))+P2·d1
(P2;(C1,W2))+P3·d1(P3;(C1,W2))=
0.4×(-0.3)+0.34×(-1.5)+
0.26×(-3)=-1.41
(6)
EX2=P1·d2(P1;(C1,W2))+P2·
d2(P2;(C1,W2))+P3·d2(P3;(C1,W2))=
0.4×(-1.3)+0.34×(-2.7)+
0.26×(-2.9)=-2.19
(7)
当非机动车首先决策,根据表2的收益矩阵得到博弈展开式如图4所示。博弈过程开始时,非机动车首先决策,随后机动车作出决策。在第一层信息节点上,在发生中等冲突和轻微冲突的情况下,其采取抢行(C2)都是其最优策略。无论非机动车如何决策,对于机动车来讲,除了在信息节点1.3上,其都会优先选择抢行以获得最大收益。但实际上,机动车与非机动车在交通系统中所处的地位差异悬殊,非机动车对冲突的严重程度感知并不明确,在信息节点1.1、1.2上,无论是选择抢行还是等待策略,其发生轻微冲突的收益差和发生中等冲突的收益差远小于发生严重冲突时的收益差。由此可以看出,非机动车选择等待是最佳决策。当非机动车选择等待决策(W2)时,机动车选择抢行决策(C1)仍是最好选择。

图4 非机动车首先决策情况下的博弈展开式


d1(P2;(W2,C1))+P3·
d1(P3;(W2,C1))=
0.4×(-1.3)+0.34×(-2.7)+
0.26×(-2.9)=-2.19
(8)

P2·d2(P2;(W2,C1))+P3·d2
(P3;(W2,C1))=0.4×0+0.34×
(-0.7)+0.26×(-2)=-0.76
(9)
综合以上结果,能够看出不管机动车或者非机动车哪一个局中人先行决策,机动车抢行(C1)、非机动车等待(W2)都是其各自的最优策略。理论分析结果虽然如此,但实际上,非机动车在交叉口处选择抢行策略而发生的交通事故屡见不鲜,所以还应该将继续重视交叉口处非机动车的安全问题。
3 结束语
本文运用博弈论分析了机动车和非机动车的决策行为。通过对右转机动车与直行非机动车冲突行为的建模分析,对机动车与非机动车的冲突行为进行了研究。结果表明,机动车选择抢行,非机动车选择等待是其各自的最优策略。
在信号控制交叉口,其每一种控制状态称为一个信号灯相位,即对各种进口道不同方向所显示的不同灯色的组合。通过调查发现,在交叉口等待的非机动车在相位变换初期更易于做出抢行策略,从而造成安全隐患;而在变换以后的相位中后期不易做出抢行策略,不易发生交通事故和拥堵现象。基于这种观察,可以采用机动车非机动车相位不同步的控制策略对交叉口处的交通流进行管理,以提高运行效率,降低交通安全风险。
除此之外,在早晚高峰期非机动车流量较大,可以在早晚高峰时段禁止右转机动车通行,同样也能达到提高效率,提高安全水平的目的。

