匝道设缝墩曲线刚构桥模型试验研究
, , ,
(中南林业科技大学 土木工程学院, 湖南 长沙 410004)
1 概述
由于城市高架及高速匝道的需要,曲线桥已成为目前应用非常普遍的桥型。该类桥因为曲线内外侧弧长相差较大、结构横向不对称及弯-扭耦合效应,导致横向受力严重不均匀甚至侧倾事故的发生。目前,国内外众多学者对此进行了广泛的研究。宫亚峰等[1]基于结构倾覆的力学原理,进行了三跨独柱连续曲线梁桥抗倾覆稳定性分析;曹景等[2]对箱形截面直线桥及曲线桥进行了抗倾覆稳定性分析;Ricardo Alvarez-Acosta et al[3]通过等截面简支曲线钢梁桥的结构响应研究,提出了1套估算曲线钢筋混凝土梁桥最大力学单元和中跨挠度的方程组;焦驰宇[4]开展了单梁法分析曲线梁桥的适用条件研究;王解军等[5]制作了三跨连续曲线宽箱梁有机玻璃模型,研究了其力学特性;Xuefei Shi[6]采用显式非线性动力有限元法对某高速公路出口匝道桥事故进行了分析;牛洪刚等[7]通过对城市公路桥梁抗倾覆验算,制定出了适用于独柱墩桥梁倾覆稳定性的验算方法和加固改造的设计方案;文强[8]研究了铁路小半径大跨度曲线连续刚构桥设计;唐云伟等[9]利用ANSYS-LS-DYNA建立了三跨连续刚架曲线桥有限元模型,进行了车辆圆周运动及超车时程的仿真计算,分析了横向力系数的规范计算结果与仿真结果的偏差及超车对横向力的影响;Taiyu Song et al[10]进行了EPC连续曲线箱梁的弯矩重分布的研究;王阳春等[11]针对小半径匝道曲线梁桥存在的墩矮、弯扭耦合严重、地震危害明显的特点,结合了一座三跨连续小半径匝道曲线梁桥的工程实例,分析比较了单梁模型、梁格模型和实体模型在模拟小半径曲线梁桥时的精度;Mohsen Am-jadian et al[12]开展了曲线桥在地震作用下的刚体运动研究。这些研究都取得了大量的成果。
但是,至今鲜有对匝道设缝双肢墩小半径曲线刚构桥的研究,首先该结构体系的双肢墩相比于整体墩而言,增大了抗推柔性简化了桥墩的布置,使得外形更适应城市桥梁的美观要求,再者墩梁固结使得结构整体性更好且利于抗震,上、下部结构整体刚度提高的同时还可望能彻底解决曲线桥的倾覆问题。故有必要开展相关研究,明确其受力性能。
本文模拟实际工程曲线桥(半径85 m,跨径60 m)的结构尺寸,根据相似原理按1/30比例设计制作3跨匝道设缝双肢墩小半径曲线刚构桥的有机玻璃模型[13-14],运用ABAQUS建立缩尺比例的实体单元有限元模型(模型1)。通过静力加载,研究其应力分布规律、挠度变化情况及内外侧受力的不均匀性,为更好反应曲线桥的受力不均匀性,引入了“不均匀系数λ”,具体为:
(1)
(2)
(3)
式中:σ0、σi分别代表曲梁的外、内侧顶(底)腹板处或双肢墩外、内侧竖向应力;w0、wi分别代表曲梁的外、内侧腹板处的挠度;f0、fi分别表示曲梁外、内侧支座反力。建立半径为40 m的1/30缩尺比例的ABAQUS实体单元有限元模型(模型2),对比分析半径大小对匝道设缝双肢墩小半径曲线刚构桥受力不均匀性的影响。
2 模型试验
2.1 模型材料与相似常数
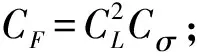

表1 试验模型的主要相似常数Table 1 The main similarity constants of the model几何常数Cl弹性模量常数CE集中力常数CF应力常数Cσ应变常数Cε3014.253 20441
2.2 试验模型与控制截面测点的布置
设计制作三跨等截面箱梁的匝道设缝双肢墩小半径曲线刚构桥有机玻璃模型,主要结构尺寸:半径为2833.3 mm,跨径2000 mm,中线跨长(666.6+666.6+666.6)mm,边跨计算跨径为650.1 mm,中跨跨径666.6 mm,箱梁高50 mm;箱梁顶板宽283 mm,厚8 mm;箱梁底板宽167 mm,厚12 mm;3个跨中横隔板厚14 mm,2个梁墩固结处的横梁宽42.5 mm;2个双肢墩呈花瓶状,其中墩顶长167 mm,宽20 mm,墩底长120 mm,宽20 mm,双肢墩之间的间距2.5 mm,墩高283 mm,具体尺寸见图1。设计2个钢支架并垫橡胶片支撑在两边桥台来模拟橡胶支座,制作2块钢板通过螺栓并胶水与双肢墩固结,钢板又通过螺丝与基础形成固结。
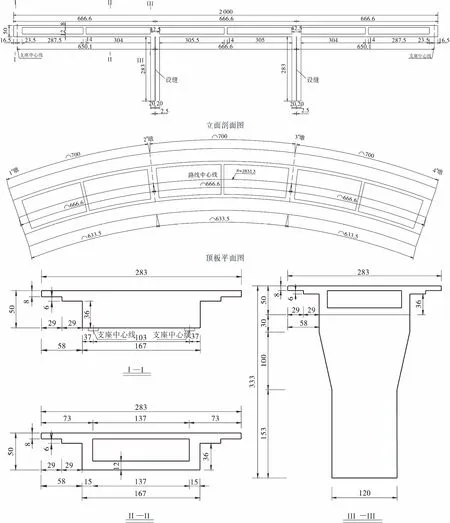
图1 曲线刚构桥模型主要尺寸(单位: mm)Figure 1 Main dimensions of curved rigid frame model (Unit: mm)
分别选取模型主梁上的边跨跨中、墩梁固结处、中跨跨中以及墩顶、墩底,共6个控制截面(分别为主梁A、B、C、D截面,双肢墩E、F截面),其中A、D,B、C截面相同,全桥控制截面布置如图2所示。A、B,E、F截面应变片布置见图3,其中外侧表示曲梁的外侧,内侧表示曲梁的内侧,边跨表示边跨侧,中跨表示中跨侧。同时,在A、D及桥台支座截面安装百分表测试模型的挠度变形。
2.3 试验方案
由于模型结构的自重较轻,为了不使加载过程中出现支座负反力,各工况加载前先在两边桥台的支座截面处进行适当的配重。加载工况通过模型结构的影响线以及考虑实验室的具体设备情况决定。拟制作两根钢支杆,在支杆两边加砝码来进行单点力或两点力的加载,同时为了试验安全,此次加载分11.2、15.2、19.2 kg共3级进行,分别测量各级荷载作用下截面的应变和变形。本次主要研究竖向中心荷载作用下匝道设缝双肢墩小半径曲线刚构桥的的应力和挠度变化规律及内外侧受力不均匀性,因此只介绍工况1(C1)中跨跨中中心加载和工况2(C2)边跨跨中中心加载2个工况的结果。
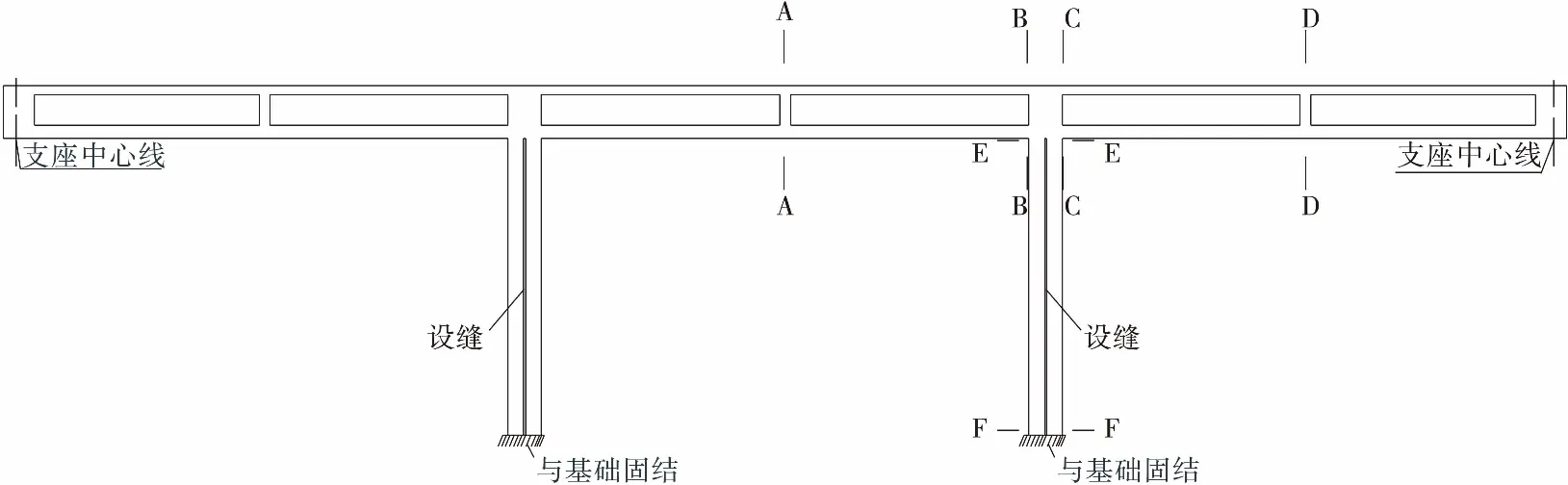
图2 全桥控制截面立面图Figure 2 Full bridge control section elevation
图3 截面应变测点布置(单位:mm)Figure 3 Section strain point arrangement (Unit: mm)

图4 模型试验工况加载位置Figure 4 Loading position of model test condition
3 理论计算及模型试验结果比较分析
采用有限元软件ABAQUS分别建立相同截面和边界条件的模型1(R=2.83 m)和模型2(R=1.33 m),两个模型均为直角坐标系下的六面体实体单元有限元模型,其中模型1共分6543个单元,模型2为6147个单元。边界条件:双肢墩墩底固结,每边桥台按比例切出2个面,将每个面耦合到各个面上中心1个点上,每边桥台2个点分别为模拟1个约束横向和竖向的固定双向支座和1个约束竖向的单向支座,如图5所示。对以上的2个工况分别进行模拟加载,对比分析模型1的试验应力、挠度值与有限元分析结果,比较模型1和模型2的有限元值的不均匀系数。

图5 工况1模型试验加载Figure 5 Model test loading under working condition 1
3.1 控制截面应力比较分析
因为加载过程中部分顶板的加载点刚好位于应变的测点位置,所以为了防止出现应力集中现象,对比分析时此类点不予考虑。图7~图10和表2、表3为荷载19.2 kg作用下模型的应力试验值与有限元计算理论值,其中“+”为拉应力,“-”为压应力。

(a) 模型1
(b) 模型2
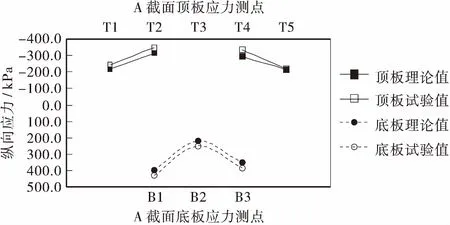
图7 工况1下A截面纵向应力的横向分布Figure 7 Vertical stress distribution of A section under working condition 1
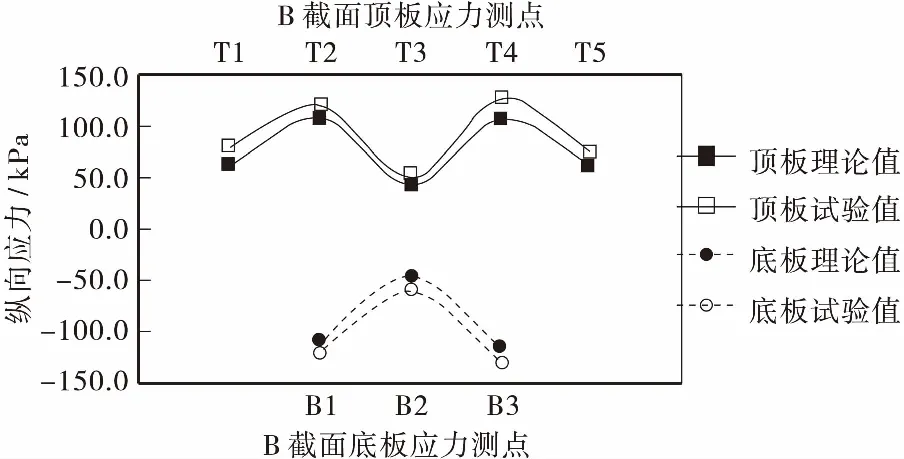
图8 工况1下B截面纵向应力的横向分布Figure 8 Vertical stress distribution of B section under working condition 1
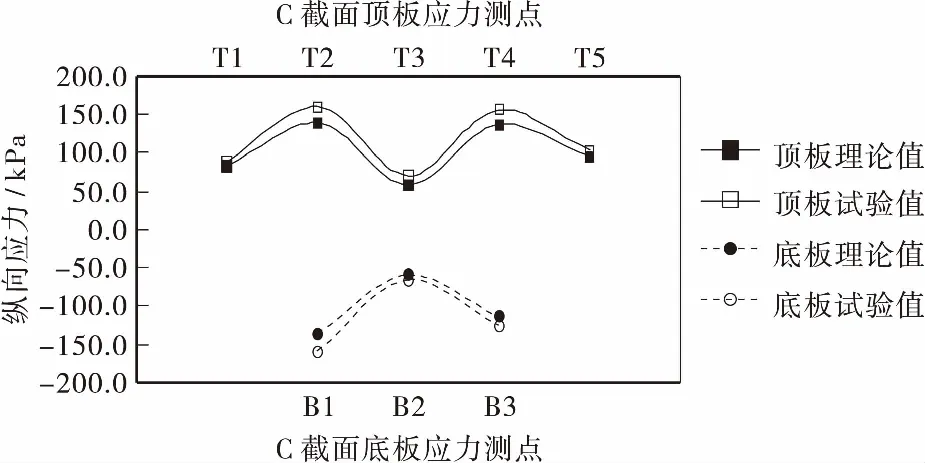
图9 工况2下C截面纵向应力的横向分布Figure 9 Vertical stress distribution of C section under working condition 2
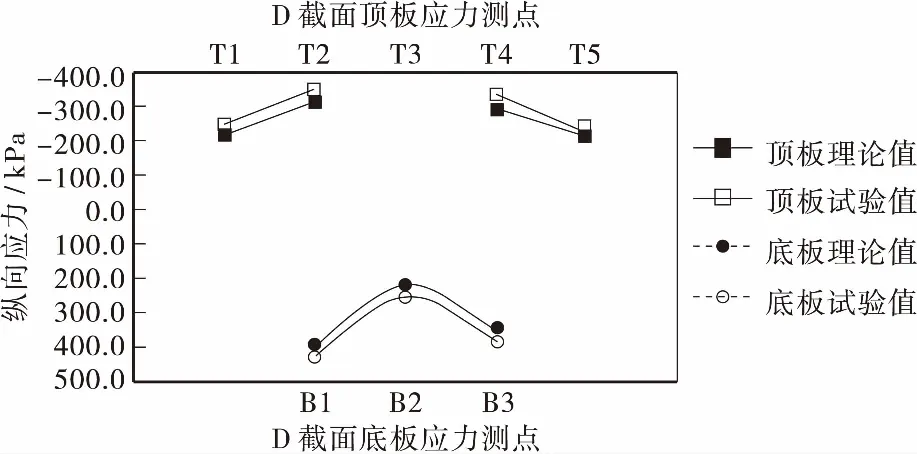
图10 工况2下D截面纵向应力的横向分布Figure 10 Vertical stress distribution of D section under working condition 2
从图7~图10可以看出,模型试验值与有限元分析的理论值基本一致,且差值一般在20%以内。箱梁截面顶、底板纵向应力峰值均出现在与腹板交界处,表明剪力滞效应明显。2个工况下底板应力最大值一般大于顶板的最大值。工况2下底板外侧应力明显大于内侧,而工况1下跨中底板内、外侧应力相差程度稍小一些,这是由于中跨两端梁墩固结的原因引起的。
由表2、表3可知,2个工况下双肢墩竖向应力的试验值与有限元计算的理论值基本一致,不同工况下中跨侧肢墩竖向应力数值与边跨侧相差较大,并且内、外侧应力数值均一定的相差,表明桥墩受力也不均匀。
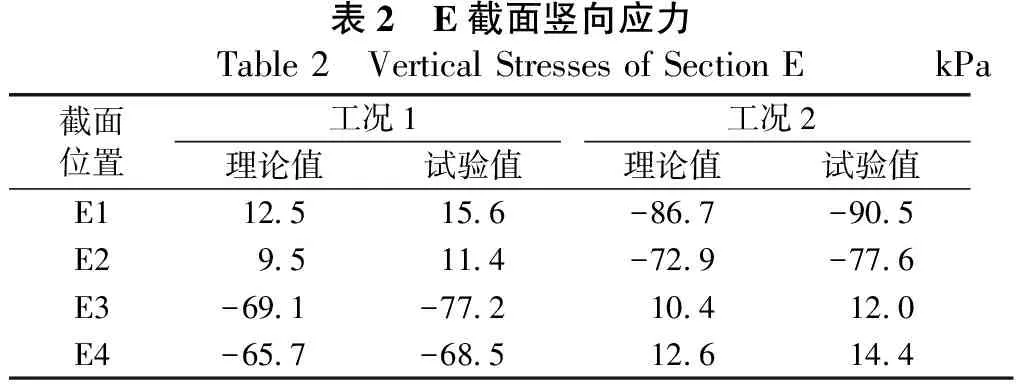
表2 E截面竖向应力Table 2 Vertical Stresses of Section E kPa截面位置工况1工况2理论值试验值理论值试验值E112.515.6-86.7-90.5E29.511.4-72.9-77.6E3-69.1-77.210.412.0E4-65.7-68.512.614.4

表3 F截面竖向应力Table 3 Vertical Stresses of Section FkPa截面位置工况1工况2理论值试验值理论值试验值F121.627.7-95.4-100.6F223.026.6-78.3-82.4F3-72.0-79.612.315.2F4-75.2-80.336.338.3
3.2 控制截面荷载挠度变化曲线
如图11、图12为荷载-位移曲线,由图可知在工况1和工况2作用下,曲线桥各测点挠度呈线性变化,表明此时箱梁处于线弹性阶段,满足试验测试要求。试验挠度值与分析得到的理论值基本吻合,但试验值一般稍大于理论值,且差值在12%以内。工况2下D截面内、外侧挠度大于工况1作用下A截面内、外侧挠度,相同工况下箱梁的外侧挠度明显大于内侧。
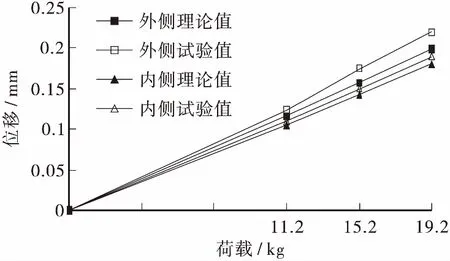
图11 工况1下A截面荷载-位移曲线Figure 11 A-section load-displacement curve under condition 1
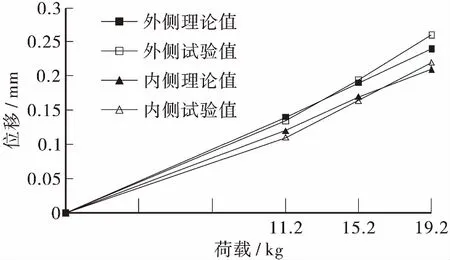
图12 工况2下D截面荷载-位移曲线Figure 12 D-section load-displacement curve under condition 2
3.3 箱梁内外侧应力、挠度,支座反力及双肢墩内外侧竖向应力不均匀性分析
基于前述分析结果,按式(1)~式(3)计算可得表4~表7。
表4为箱梁截面纵向应力不均匀系数,对于模型1,工况2下边跨箱梁底板应力不均匀系数较大,达19%(C截面)和13%(D截面);2个工况下箱梁顶板应力及工况1下底板应力不均匀系数均较小,未超过10%。由表5,箱梁边跨挠度不均匀系数为14%、且大于中跨。
由表6、表7可知,边墩内外侧支座反力及中墩墩身截面受力严重不均匀,当荷载作用在边跨跨中时(工况2),内、外侧支座均受压,不均匀系数为1.26;当荷载作用在中跨时(工况1),边墩支座出现负反力(受拉),内、外侧相差较大,不
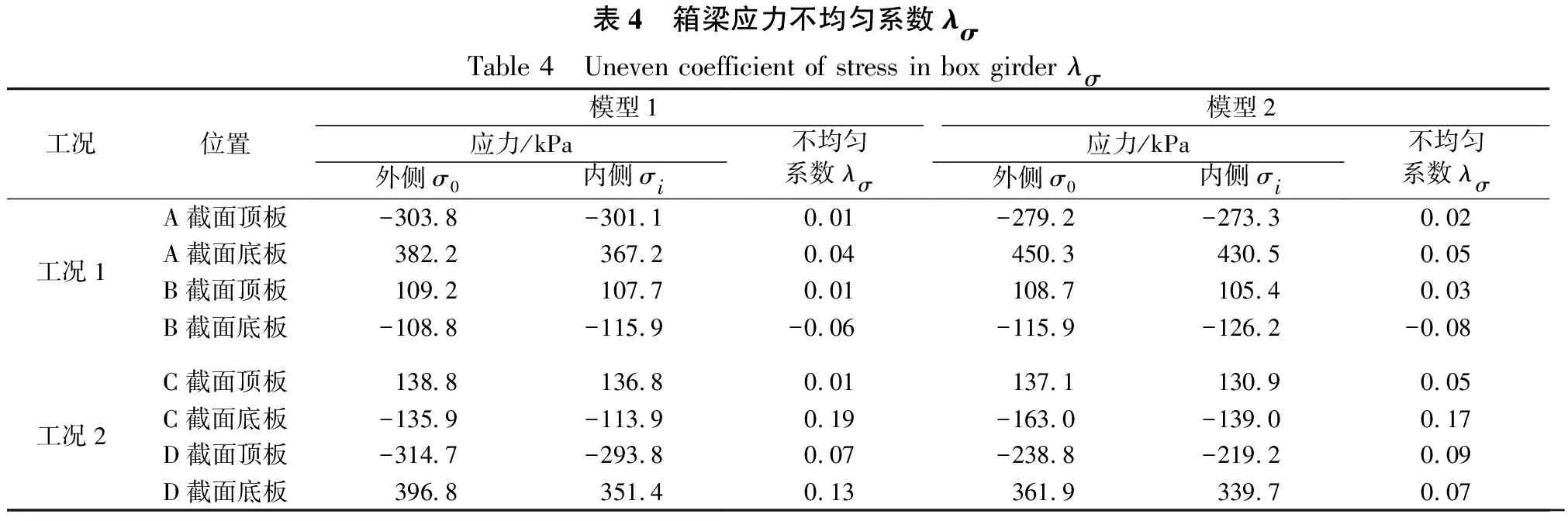
表4 箱梁应力不均匀系数λσTable 4 Uneven coefficient of stress in box girder λσ工况位置模型1模型2应力/kPa外侧σ0内侧σi不均匀系数λσ应力/kPa外侧σ0内侧σi不均匀系数λσA截面顶板-303.8-301.10.01-279.2 -273.30.02工况1A截面底板382.2367.20.04450.3 430.5 0.05B截面顶板109.2107.70.01108.7105.40.03B截面底板-108.8-115.9-0.06-115.9 -126.2-0.08C截面顶板138.8136.80.01137.1 130.9 0.05工况2C截面底板-135.9-113.90.19-163.0 -139.0 0.17D截面顶板-314.7-293.80.07-238.8 -219.2 0.09D截面底板396.8351.40.13361.9 339.7 0.07
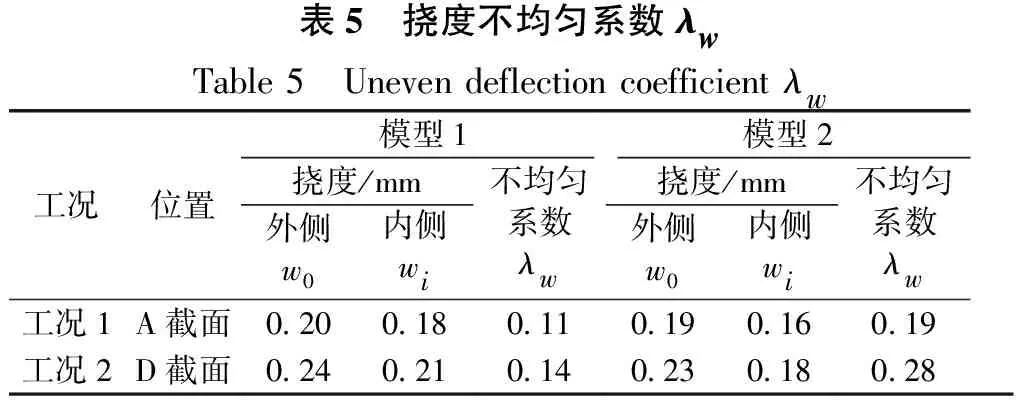
表5 挠度不均匀系数λwTable 5 Uneven deflection coefficient λw工况位置模型1模型2挠度/mm外侧w0内侧wi不均匀系数λw挠度/mm外侧w0内侧wi不均匀系数λw工况1A截面0.200.180.110.19 0.16 0.19工况2D截面0.24 0.210.140.23 0.18 0.28

表6 支座反力不均匀系数λfTable 6 Uneven coefficient of support reaction λf工况位置模型1模型2反力/N外侧f0内侧fi不均匀系数λf反力/N外侧f0内侧fi不均匀系数λf工况11#墩-7.7-2.12.67-11.10.7-16.86工况21#墩51.722.91.2661.37.4 7.28
表7 F截面竖向应力不均匀系数λσTable 7 Uneven coefficient of vertical stress in F section λσ工况位置模型1模型2应力/kPa外侧σ0内侧σi不均匀系数λσ应力/kPa外侧σ0内侧σi不均匀系数λσ工况1F截面边跨侧21.623.0-0.06 20.0 19.7 0.02 工况1F截面中跨侧-72.0-75.2-0.04 -68.1 -74.7 -0.09 工况2F截面边跨侧-95.4-78.30.22 -91.9 -73.1 0.26 工况2F截面中跨侧12.336.3-0.66 8.8 32.4 -0.73
均匀系数达2.67(但支座反力值较小)。对于桥墩受力,工况2下墩底截面内、外侧受力不均匀系数分别达22%与-66% 。
比较模型1和模型2的结果可知,半径减小除箱梁应力不均匀系数变化较小外,箱梁内外侧挠度、支座反力及墩身应力不均匀系数均增大,受力更加不均匀。
总之,荷载作用在边跨(工况2),边跨箱梁底板内外侧应力、挠度、支座反力及墩身应力的不均匀系数较大,而荷载作用于中跨时(工况1)结构受力不均匀性相对较轻,这是因为中跨两端梁墩固结的原因。随着半径减小,结构受力不均匀性总体增大,这是因为箱梁扭矩增大所致。
4 结论
通过对匝道设缝双肢墩小半径曲线刚构的试验和有限元分析比较结果,得到如下结论。
a.模型的试验值与有限元分析结果基本一致,应力相差在20%以内,挠度差值在12%以内,表明试验与理论计算结果可靠。
b.荷载作用在边跨跨中(工况2)时,边跨箱梁底板内外侧应力、挠度、支座反力及墩身应力的不均匀系数较大,而荷载作用于中跨时(工况1)结构受力不均匀性相对较轻;并且,支座反力与墩身应力不均匀性大于箱梁应力、挠度的不均匀性。这是因为中跨两端梁墩固结的原因引起的。
c.随着半径减小,箱梁挠度、支座反力及墩身应力不均匀性皆增大,这是因为箱梁扭转增大所致。

