相干与信息守恒及其在Mach-Zehnder干涉中的应用*
傅双双 骆顺龙 孙源
1) (北京科技大学数理学院, 北京 100083)
2) (中国科学院数学与系统科学研究院, 北京 100190)
3) (中国科学院大学数学学院, 北京 100049)
(2018 年 9 月 27 日收到; 2018 年 12 月 12 日收到修改稿)
自量子力学诞生以来, 相干性和互补性一直是被广泛而深入研究的两个重要课题. 随着量子信息近年来的发展, 人们引入了若干度量来定量地刻画相干性和互补性. 本文建立两个信息守恒关系式, 分别基于“Bures距离-保真度”和“对称-非对称”, 并且利用它们来刻画相干性和互补性. 具体来说, 首先从信息守恒的观点解释Bures距离和保真度的互补关系, 并由此自然推导出Mach-Zehnder 干涉仪中的Englert“干涉-路径”互补关系. 其次在量子态和信道相互作用的一般框架中讨论“对称-非对称”信息守恒关系, 并揭示其与Bohr互补性和量子相干性的内在联系. 最后, 在Mach-Zehnder干涉仪中探讨相干、退相干及互补性, 刻画两个信息守恒关系之间的密切联系.
1 引 言
互补原理是量子力学的理论核心之一, 在量子科学中具有本质的重要性和广泛的适用性[1].Bohr互补原理指出共轭的物理量具有互补性质,波粒二相性和Heisenberg不确定性关系被广泛认为是互补性的表现[2−11]. 波粒二相性的一个具体形式是干涉仪中量子的粒子特性和波动特性之间的互补关系[8], 前者通常联系于量子的路径信息, 后者则联系于干涉强度. 互补性的概念是多方面的,其定性和定量的研究都是人们关心的课题.Jaeger等[12]和Englert[8]研究了如下形式的“干涉-路径”互补关系:
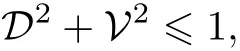
其中D是路径的可区分程度, 用来量化粒子性;V是干涉条纹强度, 用来量化波动性.V和D的具体定义和表达式见本文3.2节或文献[8]. 该互补关系已在许多实验中得到了证实和应用.
量子力学的另一个重要特征是相干性, 相干与退相干相伴, 因此与互补性密切相关, 是量子力学区别于经典力学的一个基本特征. 近年来, 随着量子技术研究的推进, 为了刻画量子力学的哪些特性会导致潜在的操作优势, 量子资源理论得到很大发展. 在资源理论的框架下, 已有大量对相干性的量化研究[13−28]. 此外, 量子相干性在量子热力学、量子计算和量子生物学等领域也发挥了关键作用[29−31], 并与最近发展起来的“对称-非对称”量化研究有着内在的联系[32−35].
量子相干是干涉现象的核心. 量子系统中相干性与波动性相联系, 而粒子性则与路径可区分性相联系. 它们之间的定量联系在干涉实验中进行了大量研究[36−38]. 近期, 文献[39]从量子力学的基本形式出发, 从交换和反交换的观点导出了在态-信道相互作用中对称性和非对称性的定量互补关系, 该互补关系表现为恒等式(一种守恒关系), 揭示了互补性和相干性之间的某些内在联系.
本文主要探讨相干与信息守恒及其在Mach-Zehnder干涉中的应用. 具体安排如下: 第2节讨论两种信息守恒关系, 其一是基于“Bures距离-保真度”的, 其二是基于“对称-非对称”的; 第 3 节首先回顾 Englert关于 Mach-Zehnder干涉仪中互补关系的不等式刻画, 其次利用第2节中的信息守恒关系给出互补性的一个等式刻画, 然后借助该等式形式的互补关系推导出 Englert的不等式, 最后探讨 Mach-Zehnder干涉仪中的相干性和互补性, 并讨论其与第2节的信息守恒关系的联系.
2 两个信息守恒关系
[40], 它们之间的Bures距离[41]可写成如下形式:
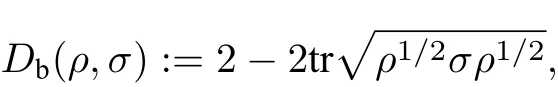

或等价地,

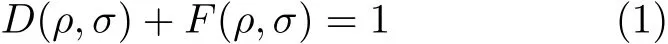
解释为一个信息守恒关系. 数学上, (1)式可由D(ρ,σ)和F(ρ,σ) 的定义平凡地得到, 但从信息的角度看, (1)式可解释为Bohr互补关系的一个刻画和量化, 将在第3 节中详细阐述这一点.
首先回顾本文中将会用到的保真度F(ρ,σ) 的几个重要性质[40]:

2) 对所有的酉算子U,
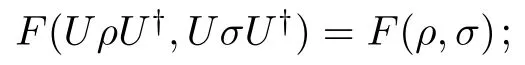
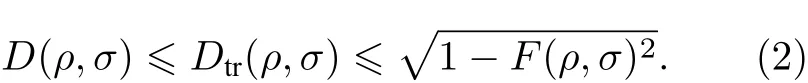
设ρ为量子态,Φ为完全正的保迹映射 (亦称作量子信道),称为 Kraus算子, 其对偶信道可表示为其中X为任意算子. 文献[39]提出可将“态-信道”相互 作用的对称部分和非对称部分分别量化为


事实上, 非对称部分I(ρ,Φ) 可解释为刻画量子态ρ相对于量子信道Φ的量子相干[39], 亦即ρ在Φ作用后的退相干. 特别地, 当Φ为保单位 (unital)信道(即Φ将单位算子1映成单位算子,Φ(1)=1 )时和I(ρ,Φ) 满足如下信息守恒关 系:
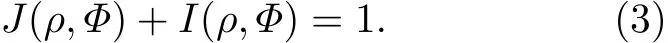
下一节将用等式(1)和(3)这两个不同但有联系的信息守恒关系来探讨Mach-Zehnder干涉仪中的互补性和相干性.
3 Mach-Zehnder干涉仪中的互补性和相干性
3.1 Mach-Zehnder干涉仪
为了在具体的框架中研究相干性和互补性, 考虑对称 MZI (如图 1 所示), 其中有 50 : 50 分束器BS和相移器PS. 分束器将输入态沿a和b两条路径分布. 用|0〉表示路径 a,|1〉表示路径 b. 设光子进入干涉仪的初始态为其 中 (rx,ry,rz) 为 三 维 实 向 量 , 且表示 Pauli算子[39]. 为了获得光子的路径信息, 引进初始态为ρiDn的路径探测器(WWD). 若光子沿路径a传播, 则探测器的初始态保持不变; 若光子沿着路径b传播, 则探测器的态经过一个酉演化变为这一相互作用导致光子与 WWD 产生关联. 因此, 在 MZI中, 探测器实际上可看作光子所处的环境. 光子与探测器的相互作用导致光子退相干, 光子部分信息流失到探测器上, 这样就可以从探测器上检测到光子的相关信息. 在 Englert干涉-路径互补关系中, 路径信息正是用探测器量子态在演化前后的迹距离刻画的.
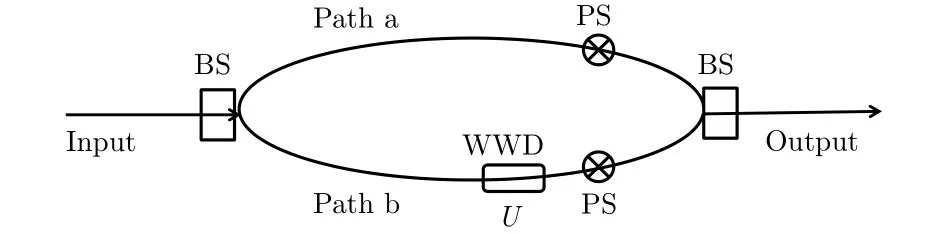
图1 对称 MZI (BS, 50 : 50 分束器; PS, 相移器; WWD,路径探测器)Fig.1. A schematic sketch of the symmetric Mach-Zehnder interferometer. BS, 50:50 beam splitter; PS, phase shifter;WWD, which-way detector.
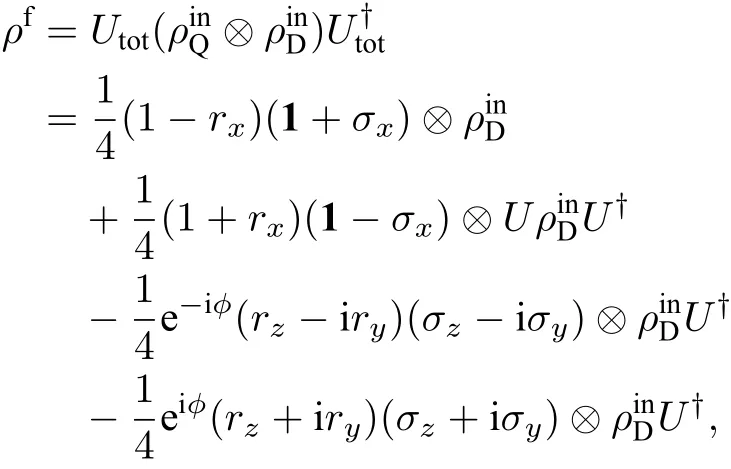
其中

对两体量子态ρf关于WWD取偏迹[40], 得到光 子的输出态

类似地, WWD的输出态为
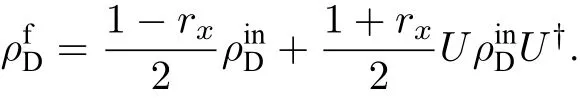
有了以上准备, 以下两小节将讨论Mach-Zehnder干涉仪中的相干性和互补性.
3.2 Mach-Zehnder干涉仪中的互补性
Bohr互补原理在MZI中具体表现为波粒二相性, 对此已有丰富的理论和实验研究[4−9,12], 其中一个很重要的工作是Englert[8]给出的波粒二相性的不等式刻画. 本节将信息守恒关系(1)解释为波粒二相性的等式刻画, 特别地, Englert的结果是该等式的推论.

区分程度紧密相关. Englert提出的量D本质上为两个量子态之间的迹距离[39], 虽然该量具有好的操作性解释, 但从信息论的角度来看, 该量有一些缺陷, 如它不是黎曼的. 与此对照, Bures 距离Db既是黎曼的又是单调的, 故利用
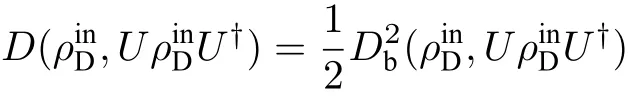
刻画粒子性具有理论上的优点. 为提供一个直观易理解的例子, 不妨考虑直角三角形的三个边长, 显然边长本身具有明确的物理长度含义, 但它们之间并无明显的数量关系, 但是如果用长度的平方代替长度, 类似于此处用Bures距离代替迹距离, 则得到勾股定理这一优美结果.
波动性与粒子性互补, 粒子性用Bures距离来刻画, 相应的波动性度量便自然地用保真度来刻画. 此外, 还可直接从V的表达式出发, 给出用保真度刻画波动性的进一步解释. 由保真度的定义和性质, 可得
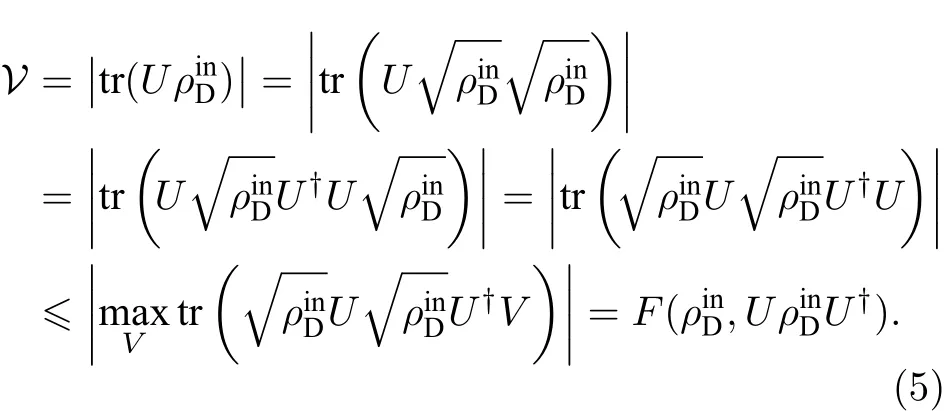
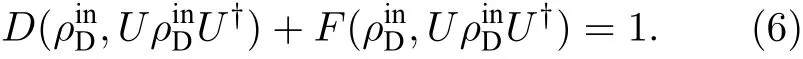
(6)式的等式关系是从现代量子信息的观点出发, 考虑光子与探测器相互作用过程中的信息流动而自然得到的. 实际上, Englert的互补关系(4)式可由上面的等式关系(6)式直接得到

最后一个不等式可由不等式(2)和(5)直接得到.
3.3 Mach-Zehnder干涉仪中的相干性
上面的讨论指出在MZI中光子与探测器相互作用, 导致光子退相干, 部分信息流失到探测器上.本节具体计算Mach-Zehnder干涉仪中的相干性,并揭示其与波粒二相性之间的密切关联. 在上述MZI中, 考虑信道
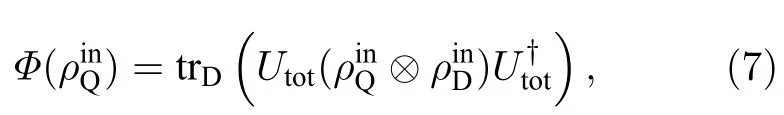
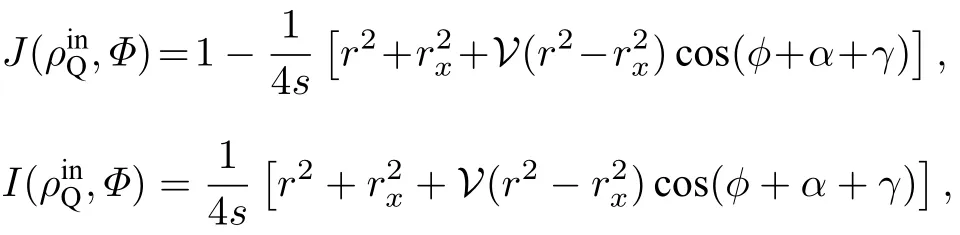
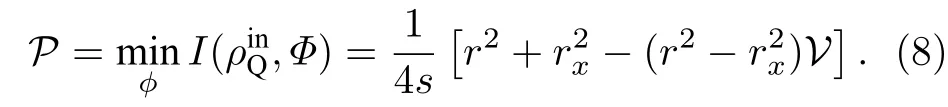

由(8)和(9)式, 可得到波粒二相性的另一个等式刻画

利用不等式 (5)式, 可得到P的下界和W的上界 为

因此, 信息守恒关系(1)式与波粒二相性的等式刻画(10)式紧密相关, 且当不等式(11)和(12)变为等式时, 两种守恒关系一致. 特别地, 当取特殊的量子态, 如时,
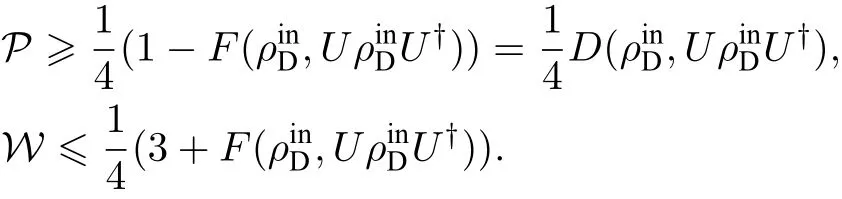
因此, 基于相干给出的波粒二相性的刻画中的粒子性度量P的下界可用D刻画, 而波动性的度量W的上界可用F刻画. 这与前面用信息守恒关系(1)式来描述互补性原理是一致的.
4 结 论
本文讨论了“Bures-保真度”互补关系和“对称-非对称”互补关系, 并将它们解释为信息守恒关系.作为应用, 由信息守恒关系直接推导出Englert的“干涉-路径”不等式. 进一步利用信息守恒关系揭示了Mach-Zehnder干涉仪中互补性与相干性的关系, 证明了可区分程度是态关于信道的非对称性(相干性)的下界, 而保真度是态关于信道的对称性的上界. 我们期望“对称-非对称”守恒关系能为相干性与互补关系的研究提供一个统一的框架.

