跳幅度为常数的跳-扩散模型的校正

高 雄, 张素梅

(西安邮电大学 理学院， 陕西 西安 710121)

期权是指在将来某一时间内或者在某一指定时刻以约定价格买入或卖出某一产品的合约[1]，是基本的金融衍生品之一，是一种有效的规避风险工具。标准期权通常可分为看涨期权(购买权)和看跌期权(出售权)。根据交易时间的不同，期权可分为欧式期权和美式期权[2]。欧式期权只允许买方在到期日进行交易，而美式期权则允许在到期日或到期日之前的任何一个营业日进行交易。欧式期权在到期日提出行权交易，卖出期权的个人、机构和做市商才会被按比例分派行权交割任务，这样可以避免额外的交易成本。本文研究欧式期权定价。

Black-Scholes(B-S)模型是金融市场上经典的期权定价模型[3-4]，由于该模型假设太理想化，无法解释资产收益的尖峰厚尾和波动率“微笑”现象。如文献[5]运用B-S模型，得到资产价格与实际市场价格不符，且存在较大差异。文献[6]在B-S模型基础上，考虑红利的影响，分别从连续支付和离散支付红利的不同形式的模型出发，引入红利因子修正B-S模型，但其使用的蒙特卡罗模拟计算效率较低，需要大量的随机抽样才能得到结果。文献[7]利用B-S模型对上证50ETF期权定价中的5个参数进行分析，发现模型中有一些理想的假设，在某种程度上限制模型的应用，无法解释资产收益的尖峰厚尾和波动率“微笑”现象。

为了预测期权的实际价格，学者们对B-S模型的改进主要分为以下几个方面：第一，在标的资产价格运行的随机B-S模型中加入跳跃部分，得到跳-扩散模型[8]，能够更好地解释实际资产收益呈现出的微笑和倾斜特征，但它不连续过程的假设给预测期权定价带来了困难；第二，修正标的资产价格的波动率是常数的假设，加入随机因子，引入随机波动率模型[9]。由于经济危机、自然灾害等重大突发事件的出现，使得实际资产价格分布呈现出间断的“跳空”现象，相对于随机波动率模型，跳-扩散模型能较好地反映这种资产价格的变化规律。跳-扩散模型除了能刻画股价实际波动的尖峰、厚尾以及波动率微笑特征外，还可以得到许多路径依赖型期权的闭式解，如文献[10]引出双指数跳-扩散模型并给出了障碍、回望及永久美式期权的解析解，受到许多学者以及金融业界人士的普遍关注。

目前关于金融衍生品的研究大多集中在定价领域，对于模型校正的研究还存在不足。由于参数估计[11]通常会导致大规模的优化问题，近年来，智能优化算法[12-13]的发展给非线性参数模型估计带来了新方法，但该算法的参数设置对优化结果的影响较为显著，需要大量的迭代次数才能得到好的优化结果。文献[14]利用极大似然估计校正双指数跳-扩散模型，但极大似然估计在应用中存在不足。一方面，它难以实施，为了得到模型参数的初始估计通常需要4～7 h；另一方面，需要考虑参数的容许区间，避免似然函数变得无穷大。

考虑到通过B-S模型得到的价格与实际市场价格不符的现象，本文拟在跳幅度为常数的跳-扩散模型下，基于收集到的实证数据，运用非线性最小二乘法，以实验值和市场值的误差平方加权和作为目标函数，利用MATLAB中lsqnonlin函数进行参数估计，为跳幅度为常数的跳-扩散模型校正提供一种新方法。

1 构建跳幅度为常数的跳-扩散模型

期权定价模型取决于原生资产价格的演化模型。在时间连续情形下，原生资产价格演化可以通过一个随机微分方程来描述，在此基础上，期权作为金融的衍生物，期权的价格确定是一个偏微分方程的定解问题。

定义一个完备概率空间(Ω,F,P)，其中Ω表示样本空间，F表示信息流，P为风险中性概率测度。设标的资产在t时刻(t∈[0,T]，T为期权的到期时间)的价格为St，其满足的随机微分方程为

(1)

其中：r为无风险利率；σ为波动率；{W(t),t∈[0,T]是{Ω,F,P}上F适应的标准布朗运动；常数h为风险资产价格的相对跳跃幅度；{N(t),t∈[0,T]}是{Ω,F,P}上F适应的强度为λ的泊松过程；N(t)描述了在t时刻偶然的价格波动引起的回报，如果在t时刻跳发生，dN(t)=1，否则为0。

设V=V(St,t)表示欧式期权价格，构建t时刻投资组合为

Πt=V-ΔtSt。

(2)

其中Δt表示t时刻卖出的股票份额。

设跳跃部分来自于具体公司信息的披露，表示为与市场无关的“非系统”风险，可以认为t时刻投资组合Πt的期望收益率是无风险利率r，因此，t时刻投资组合Πt的期望收益为

E(dΠt)=rΠtdt。

(3)

在[t,t+dt]时间间隔内，股价有以下两种情况。

第一种情况，令事件P1表示St不发生跳跃，由伊藤公式[15]得到P1事件下投资组合的增量为

(4)

第二种情况，令事件P2为St发生跳跃，P2事件下投资组合的增量为

dΠt=V(St+hSt,t)-V(St,t)-ΔthSt。

(5)

由式(3)可知，投资组合的期望收益满足等式

rΠtdt=λdt[dΠt]+(1-λdt)[dΠt]。

(6)

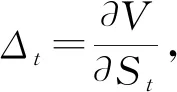
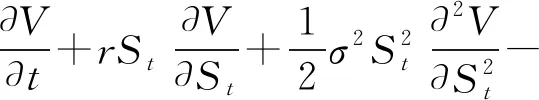
(7)

设K是执行价格，则方程(7)满足的边界条件V(St,T)为

V(St,T)=max (St-K,0)。

(8)

同时，方程(7)满足的初值条件V(0,t)为

V(0,t)=0。

(9)

根据式(1)所满足的偏微分方程(7)，结合式(8)和式(9)，即得期权价格。

2 模型校正

2.1 欧式期权定价

有限差分方法作为数值方法的一种，相对于其他求解方法，更加稳健、有效及精度高，被广泛应用于期权定价。偏微分方程求解的有限差分法[16]是利用网格线将定解区域化为离散点集，通过适当的途径将微分方程离散化为差分方程，即构造差分格式，把偏微分方程定解问题化为代数方程组，进一步求解方程组，得到定解问题的解在离散点集上的近似值组成的离散解，可把连续变量的问题转化为离散变量的问题。

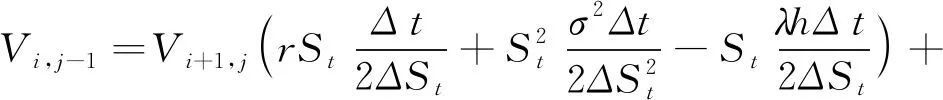
(10)

其中：Vi,j表示期权价格在资产价格和时间上的均匀网格划分；ΔSt表示资产价格在网格上的步长；Δt表示时间在网格上的步长。

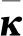
(11)

(12)

式中

zi表示第i个网格的加权因子。

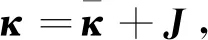
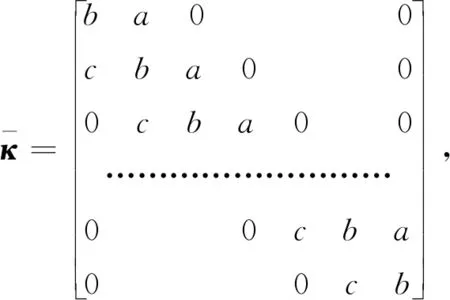
Vn-1=κVn，(1≤n≤N+1)，

利用边界条件采用向前欧拉格法[17]即可求得期权价格。

2.2 非线性最小二乘法

期权定价是在给定模型参数基础上计算期权的价格，模型校正是通过市场价格反推出理论模型的参数值，因此模型校正和期权定价互为反问题。若模型是跳-扩散模型，通常无法保证存在唯一解。非线性最小二乘法[18]是以误差的平方和最小来估计非线性模型参数的一种参数估计方法。按一定的规则选择若干组参数值，分别计算它们的目标函数值并比较大小，选出使目标函数值最小的参数值，采用非线性最小二乘法得到的最优模型参数为

(13)

设参数集初始值估计为θ0，将期权的中间价格作为市场价格，则模型价格与市场价格之间满足的关系式为

(14)

其中：ηε是市场第ε个期权的出价；δε是市场第ε个期权的开价。式(14)表示不要求模型价格准确的复制市场价格，一般在出价和开价区间内。这在校正过程中是合理的，因为建模过程总是在误差容许范围内产生要求的估计。

本文使用Matlab软件中的lsqnonlin函数实施校正算法，计算出的最优解和参数的初始值有关，虽然得到的解可能不是全局最优，但只要满足式(14)，意味着求出的最优解在误差范围内是可以接受的。

2.3 模型校正算法步骤

模型校正分为欧式期权定价和最优参数的求解，收集并筛选标准普尔500指数期权在2018年12月4日的抽样数据，具体步骤如下。

步骤1利用式(10)计算得到欧式期权价格。

步骤2得到跳幅度为常数的跳-扩散模型的参数集θ的初始估计θ0。选择加权因子ωε，根据式(14)计算输入误差。将得到的输入误差值再代回式(14)得到参数集θ的初始估计θ0。

步骤3计算由模型得到的期权价格和市场价格之间偏差。

步骤4将步骤3得出的结果代入式(13)可得到跳幅度为常数的跳-扩散模型的最优参数值。

3 实证分析

实证分析使用标准普尔500指数期权[19]在2018年12月4日的抽样数据，数据是由168个看涨期权价格组成，执行价格在2 700元到2 800元变动。每个期权的出价和开价均已知。期权的到期时间从45天到300天不等。由于期权价格对利率不灵敏，且利率在每天的基础上变化很小，因此，可以设定无风险利率为年利率0.13%，且假设市场无分红。

利用lsqnonlin函数实施校正算法。根据式(14)，通过不断地调整初始参数值 进行重新校正。选择两组初始值对跳幅度为常数的跳-扩散模型进行参数估计，校正结果如表1所示。

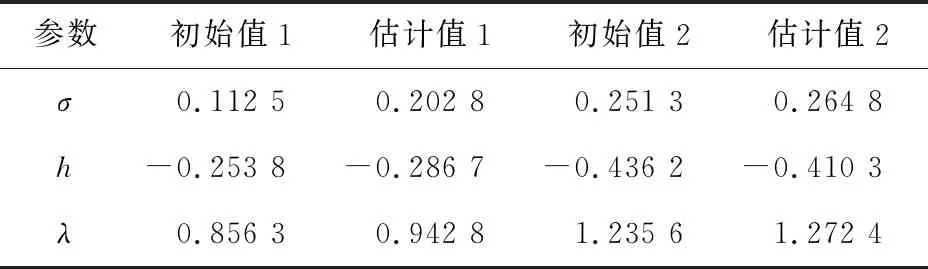
表1 两组初始值的校正结果

由表1可以看出，校正结果整体出现细小的波动。随着每个初始参数值的增加，初始值2与估计值2之间误差减小。表明通过校正得到的估计值2为模型参数的局部最优值，更加符合实际市场的模型参数。

为检验校正的效果，使用4个校正测度[20]，平均相对百分比误差(average relative percentage error,ARPE)，平均绝对百分比误差(absolute percentage error,APE)，均方根误差(root mean square error,RMSE)和平均绝对误差(average absolute error,AAE)。设ARPE为ω1，则

(15)

其中：Cmod为模型的价格；Cmar为市场价格。

设APE为ω2，则

(16)

其中mean(·)表示求均值。

设RMSE为ω3，则

(17)

设AAE为ω4，则

(18)

将由式(1)得到的期权价格和抽样数据中的市场价格，代入上述4个校正测度，得到跳幅度为常数的跳-扩散模型校正误差结果如表2所示。

表2 校正误差结果

从表2可以看出，ω1与ω2两个校正测度之间的误差非常小，不超过0.082，ω3与ω4测度之间的最大误差为0.412 8，表明模型得到了较好的校正。

利用表1中的估计值2作为模型参数，得到跳幅度为常数的跳-扩散模型下的欧式看涨期权价格，再将其作为市场价格带入B-S模型的定价公式反推出隐含波动率，绘制出该模型在不同到期日下的隐含波动率变化曲线，如图1所示。

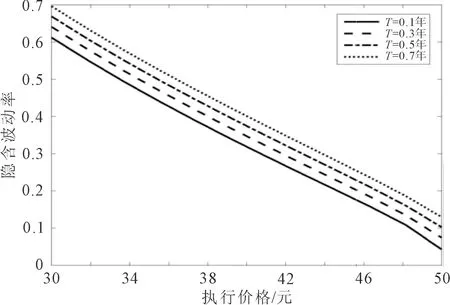
图1 不同到期日的隐含波动率曲线

由图1可以看出，在期权到期时间相同的情况下，跳幅度常数的跳-扩散模型的隐含波动率与执行价格成反向关系，即随着执行价格的增加而逐渐下降。在期权的执行价格相同时，随着到期日的增加，波动率逐渐增大，出现波动率倾斜的现象，弥补了B-S模型波动率是常数的缺陷，表明提出的跳幅度为常数的跳-扩散模型，更加符合实际市场。

根据表2中的估计值2绘制跳-扩散模型三维隐含波动率图。对于估计值2中的3个参数分别绘制隐含波动率三维图像。当波动率 的取值分别为0.202 8、0.264 8时，其结果如图2所示。

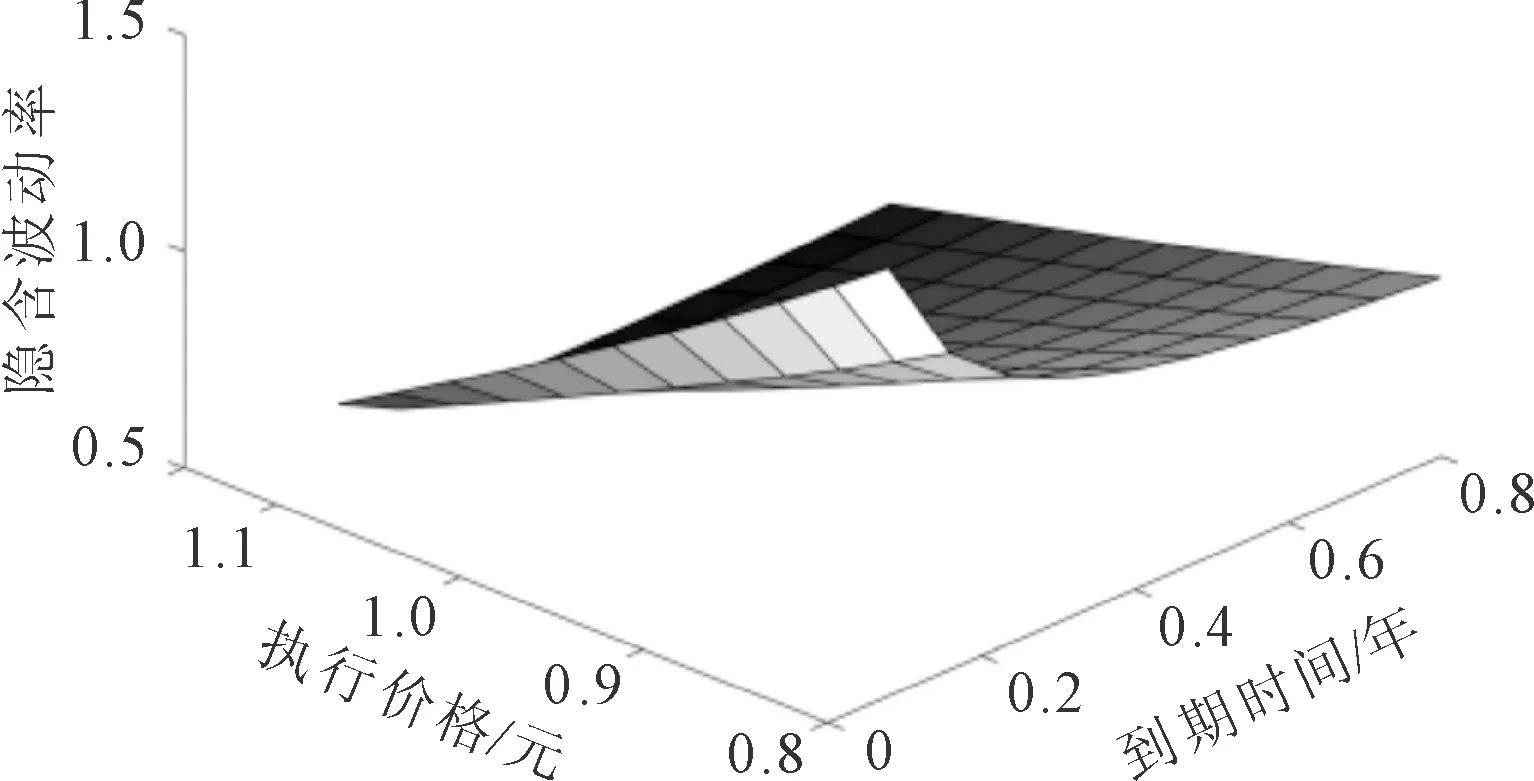
(a) 波动率σ=0.202 8

(b) 波动率σ=0.264 8

当h的取值分别为-0.286 7、-0.410 3时，其结果如图3所示。

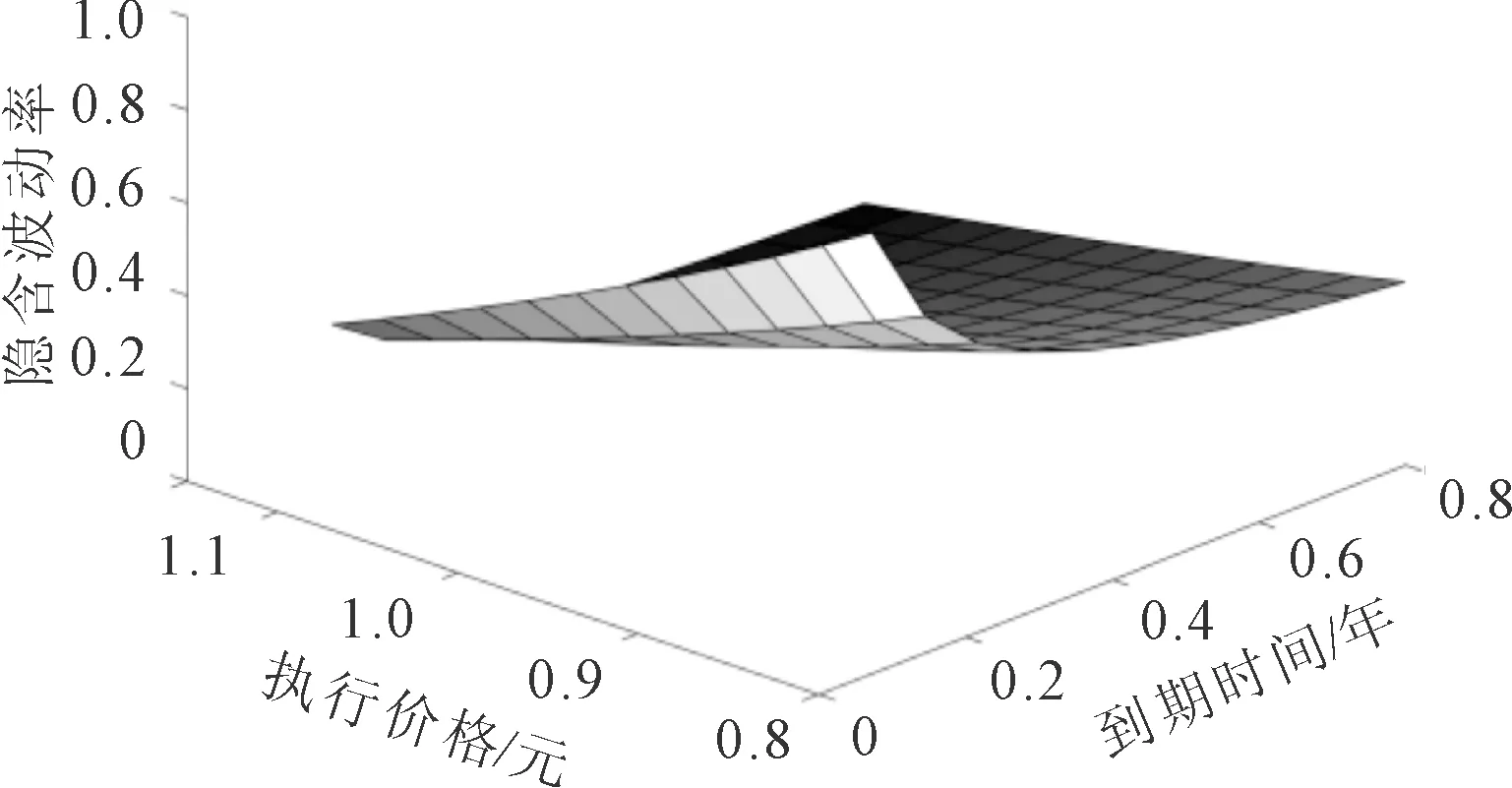
(a) 跳跃幅度h=-0.286 7

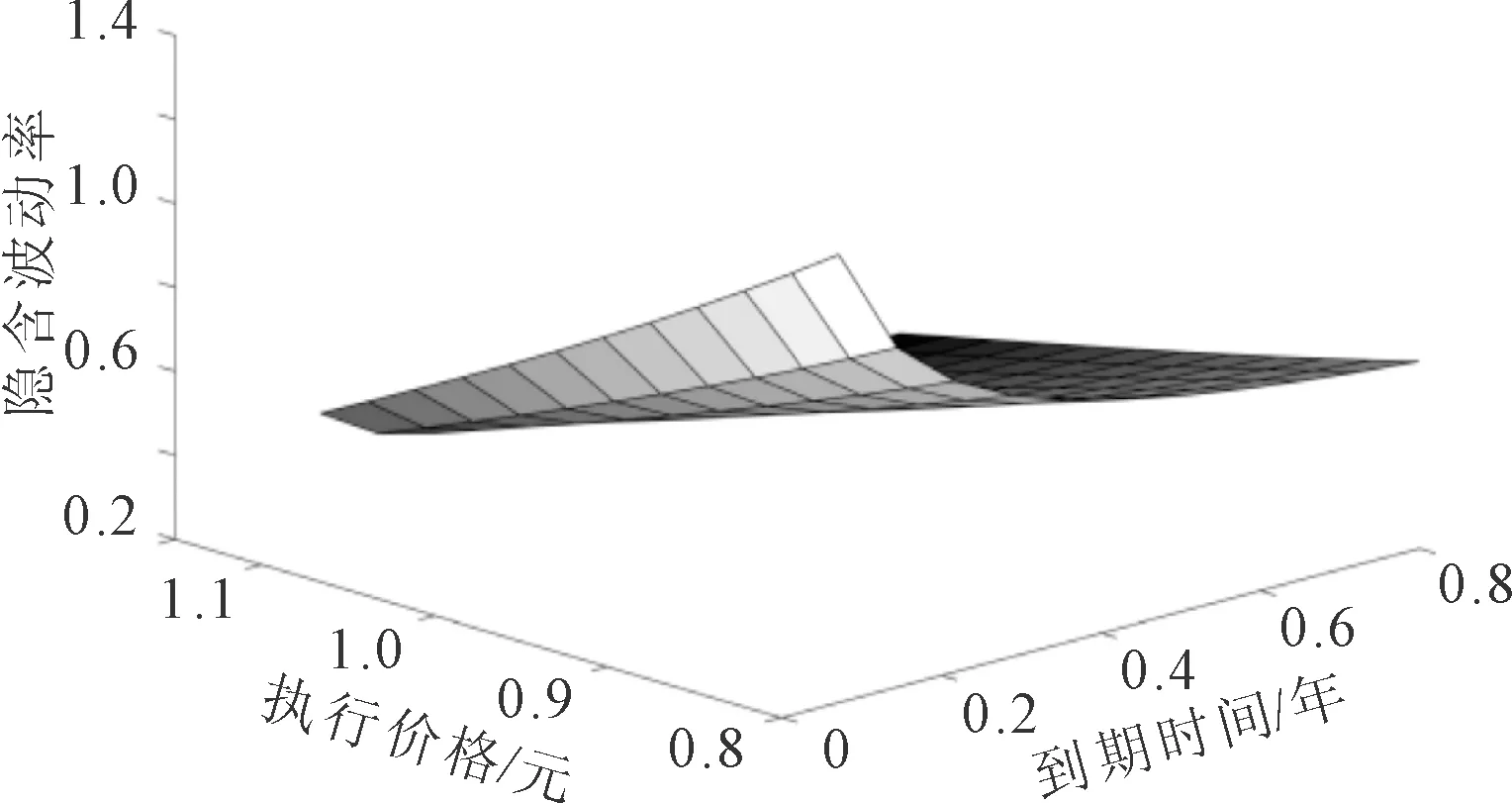
(b) 跳跃幅度h=-0.410 3

当λ的取值分别为0.942 8、1.272 4时，其结果如图4所示。

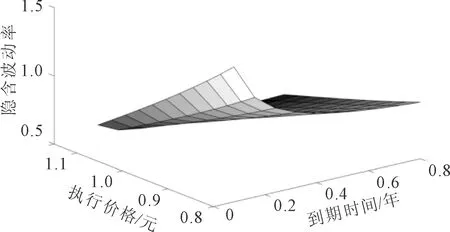
(a) 跳跃强度λ=0.942 8

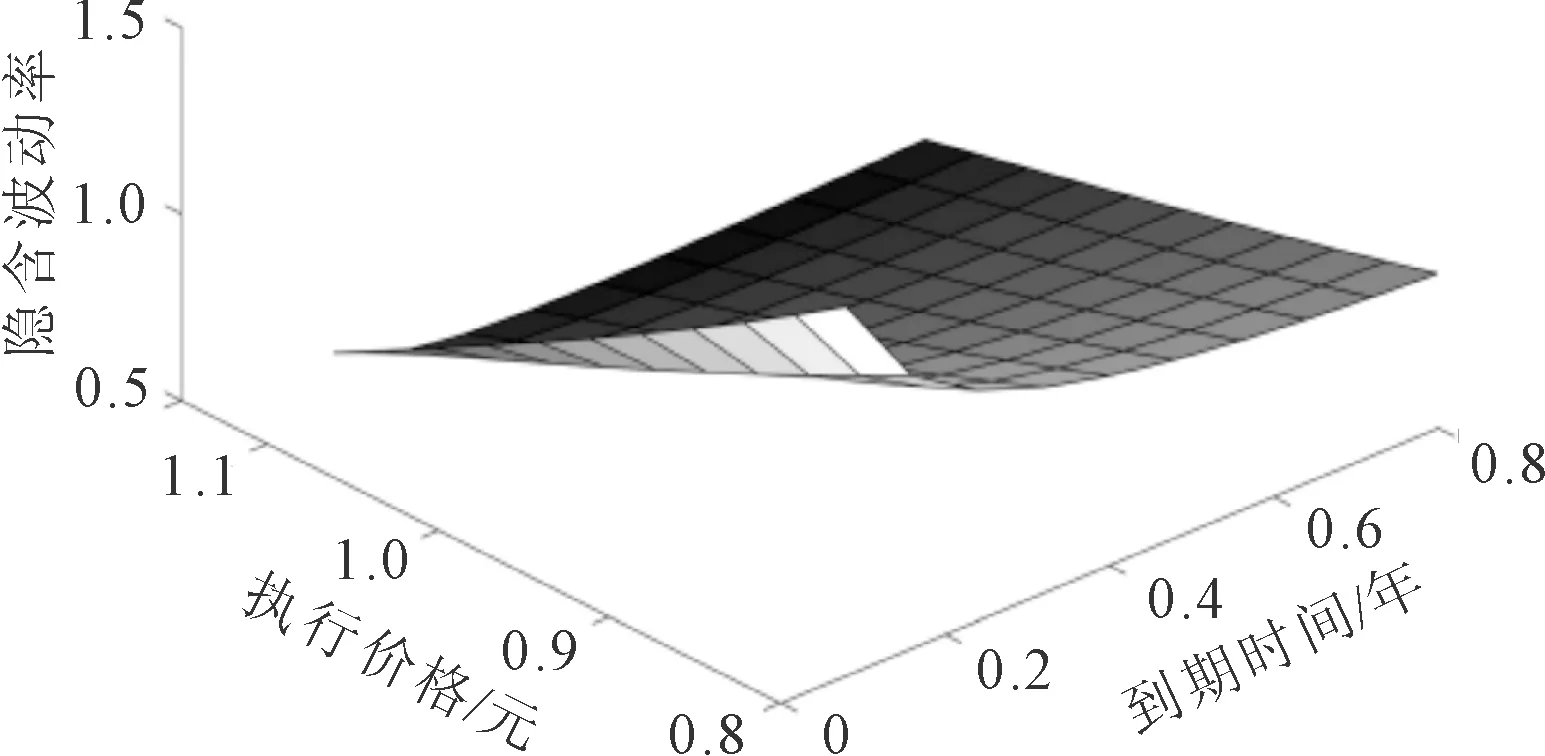
(b) 跳跃强度λ=1.272 4

由图2、图3和图4可以看出，跳-扩散模型隐含波动率三维图像不是对称的，体现出明显的“波动率微笑”特征。从图2可以看出随着波动率σ的增大，期权的隐含波动率图像变化明显；从图3可知随着跳跃幅度h的减小，隐含波动率的变化相对变化缓慢；从图4可知，随着跳跃强度λ的增大，隐含波动率图像变化明显。由此可知，波动率σ和跳跃强度λ的变化对隐含波动率的影响相对较大。

上述结果表明，随着检验到期时间和跳参数变化对隐含波动率的影响，所提出的跳幅度为常数的跳-扩散模可以修正B-S模型的波动率曲线是一条直线的假设，能够解释实际市场资产收益变化的波动率呈现的“微笑”特征，表明该模型的校正算法具有稳定性和实用性。

4 结语

运用实际数据和校正算法对跳幅度为常数的跳-扩散模型进行了校正。提出了跳影响下的市场模型，利用非线性最小二乘方法，将模型和校正方法应用于标准普尔500指数期权进行实证分析，得到模型的最优参数。绘出了跳幅度为常数的跳-扩散模型在不同到期日下的隐含波动率变化曲线图。检验跳参数对隐含波动率图像的影响，其中波动率 和跳跃强度 的变化对隐含波动率的影响较大。结果显示，跳幅度为常数的跳-扩散模型修正了B-S模型的波动率曲线是一条直线的假设，解释了实际市场资产收益变化的波动率呈现的“微笑”特征，但资产收益的“尖峰厚尾”、“波动聚类”现象没有得到很好的体现。