基于属性相关性的KNN近邻填补算法改进

谢霖铨， 赵楠， 徐浩， 毕永朋

（江西理工大学理学院，江西 赣州 341000）

0 引 言

高速发展的经济社会产生了海量的信息，因某些数据暂时无法获取或在获取过程中的粗心导致一些数据遗漏的情况经常发生，且基本是无可避免的.然而，这些缺失数据项很有可能携带该数据对象的重要信息，若直接利用这些带有缺失的数据进行数据挖掘或数据分析，其得出的结果对决策会存在一定的影响，即包含缺值的数据会使挖掘过程陷人混乱，导致不可靠的输出[1].所以，在数据处理分析之前，对缺失数据的预处理成为一项很重要的准备工作[2].对缺失数据的预处理通常是删除、寻找替代值或是不处理.删除数据简单易行，但是有很大的局限性，还会附带删除数据中隐藏的很多原始信息.寻找替代值即数据的插补，是最常用的方法，插补的基本原理是利用一些现成的规则或是合理的方法推测插补值或者替代值[3].

近年来，数据填补不再简单的以数据的数值大小作为计算准则，粗糙集合理论[4]、关联规则[5]等更多的改进算法相继被提出来[6].近邻均值填补是单一填补的一种方法，操作简单，其受噪声影响比较大[7]，文献[8]则介绍了一种基于噪声处理的近邻填补算法.主成份分析 （Principal Computer Analysis，PCA）是Karl parson[9]于1901年提出的一种多元统计分析方法是经典的特征降维算法，根据原始数据集的协方差矩阵和特征值特征向量计算新的向量基最，终将原始数据投影到新的向量基中，并使这些新变量尽可能多地反映原变量的信息量.统计学领域对缺失数据填补方法也有广泛的研究，如回归法[10]、热卡填补（Hot Deck Imputation）[11]、最大期望法（Expectation Maximization）[12]、随机回归填补法等，这些方法对处理缺失数据，建立完备的数据集起到很重要的作用.用于数据挖掘与机器学习的各种算法对缺失数据填补都有借鉴，如基于神经网络的缺失填补算法[13]、基于K最近邻法（K-Nearest Neighbor,KNN）[14]、基于贝叶斯网络的填补算法[15]、基于聚类的填补算法、基于关联规则[16]的填补算法.通过实验证明，即使一些比较简单的、填充效果一般的算法，都明显的提高了算法的执行和效果.

文中主要研究的是KNN最近邻算法在数据填补方面的运用.KNN最近邻填补算法是数据填补的一种常用方法，以其简单易明的算法原理和方便的操作过程深受广大学者的青睐，也被广泛的应用在很多实际问题中，比如人口统计或者水文数据的分析.KNN算法最早是由Cover和Heart[17]在1968年提出了最原始的计算模型.根据K近邻算法存在的缺点，一些对于它的改进也响应而出，文献[18]介绍了一种针对噪声处理的KNN算法，文献[19]则是结合了哈希表对KNN填补算法进行改进，文献[20]利用粒子群优化方法的随机搜索能力指导KNN算法近邻搜索，文献[21]将支持向量机算法和KNN算法相结合来提高算法的精度.本实验则考虑了属性的相关性，应用主成分分析过程的相关系数矩阵，对传统KNN进行优化.

1 KNN填补算法和PCA算法

1.1 KNN填补算法

首先计算目标数据集（包括含有数据缺失的数据记录项，m是数据记录数量，n是数据维数）和数据集中所有的完全值数据记录的欧式距离，在所有的完全值数据记录中选择出与目标数据欧式距离最小的k个数据记录作为目标数据的最近邻，k最近邻数据记录相应位置的加权平均值即可作为数据记录缺失数据的评估值.

1）数据初始化，构建完整数据集矩阵：（x1,x2,…,xj,…,xm）T，其中[X]r是数据的第 r个属性，r≤n，m为样本数量；

2）计算目标值与数据矩阵中其他数据记录的欧式距离，给定一个缺失实例xir：

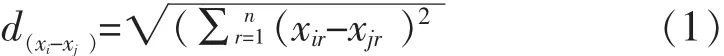
3）选出距离最小的k个距离对应的数据记录作为目标数据的k近邻数据；

4）计算目标数据的k个最近邻目标的权值：

5）算出缺失值的替代值：

其中，xkr表示最近邻相应属性的数值.

1.2 PCA算法

主成分分析 （Principal Component Analysis，PCA）是一类处理高维数据的算法，实质将高维的数据投影到低维空间上，最小化属性间相关性.计算过程中的协方差矩阵，是来反映各个纬度之间的相互关系[22].如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值.如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值.如果是统计独立的，那么二者之间的协方差就是0[23].

协方差作为描述和相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异，因此，在应用协方差度量相邻数据相关关系时，首先要保证数据在同一物理量纲下，所以在实验时先对数据矩阵做标准化处理.

2 改进的KNN填补算法过程

2.1 构造数据的相关性系数矩阵

第一步：初始化数据矩阵，构建完整的数据矩阵Xm*n，m表示数据有m条数据记录，n表示数据记录的维数.将所有缺失数据标记，以待下一步处理.

第二步：数据标准化，目的是使数据的平均值为0，标准差为1，这样可以使得不同量纲的数据放在同一矩阵.数据标准化的数学公式是：

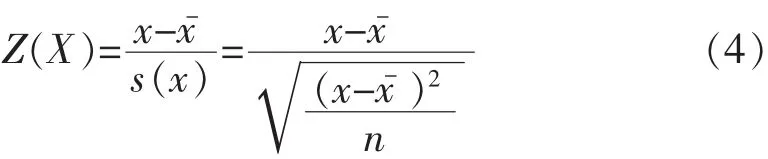
第三步：对标准化后的数据矩阵求协方差，协方差是一种用来度量两个随机变量关系的统计量，公式为：

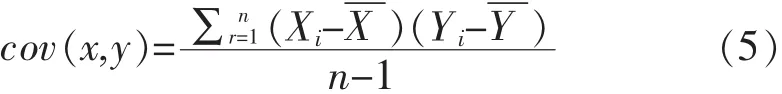
对于一个n维的数据矩阵，由于数据两两之间的便可以得出一个协方差.那么这个n维的数据便可以得到一个n*n的协方差矩阵.

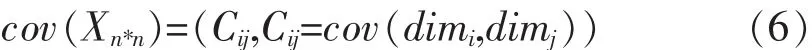
若xi表示矩阵的第i个属性，可以表示为：

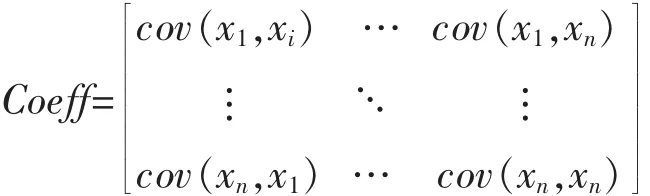
2.2 计算KNN算法的估计值

这一部分算法主要是KNN填补算法的过程.

第一步：计算完备数据集的欧式距离.首先因为缺失数据基本是随机的，所以可能在任何一维或者某条数据记录里出现，因此在计算距离时，仅仅将没有缺失的数据考虑进来.不过这里只是在计算两两之间的距离时，忽略那些有缺失的维数.

第二步：由于整个算法过程都与距离的有关系，距离的大小决定着后续选取的K个近邻的质量和选取准确度.在前两步的基础上计算矩阵X的欧式距离矩阵，用Xi表示第i条数据记录.

矩阵的每一行就代表X中的其余行从第一行开始和本行的欧式距离.

第三步：从原始数据的第一行第一列开始遍历寻找缺失值xij，那么它所在的行数就是i，第i行所对应的距离矩阵即是dis的第i行.然后确定要使用的近邻的个数K，选取dis对应行的最小的K个数值构成向量：

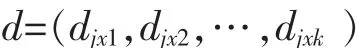
针对每一个距离数值确定它对应的数据项得行数，再找到缺失值在这行数据中对应的同一属性的数值.距离和这个数值的乘积便是一个邻居的加权值，最终的K个邻居加权值的和除以距离的和的加权均值就是最后KNN算法所求得的替代值x0.

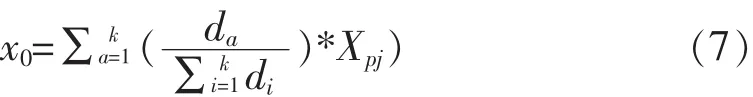
xpj是最近邻相应位置的数值.p是距离矩阵的列数对应原数据矩阵的行数.

2.3 计算维度相关值得到最终填补值

利用第一步所得的协方差矩阵和K个近邻数据组成的近邻矩阵，通过计算得到一个和维度相关的量，将这个量称为维度相关量.

第一步：考虑到每一个属性对应数值的大小不一样，所以用每一个数值减去本属性下的统计值的均值作为计算的标准，这个值被称为偏差，它表示一个数值偏离中心的程度.

m0是这个属性中未缺失的个数，xij就是对应的统计值.

第二步：求出用第一步所求的差值和相应协方差矩阵对应值，就是这个属性对于缺失数据所在维度的影响大小.对K个近邻中所有不是缺失数据的观测数值做同样操作，最后所得的数值相加后取均值，得到其余完备数据的属性和这个缺失值所对应属性的维度相关数值.

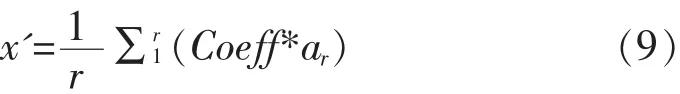
r是数据项中这一行中未缺失的数据个数，也是现实条件下能统计到的对缺失值产生影响的维度数目，Coeff是ar对应的协方差数值.

第三步：将第二部分中所求的估计值和维度相关量相加，得到我们最终改进算法后的缺失值的估计值.

3 实验结果与分析

3.1 检验方法

比较实验前后填数据果和原始数据的差别，所以采用均方根误差RMSE（Root Mean SquareError）评价缺失数据填补效果.

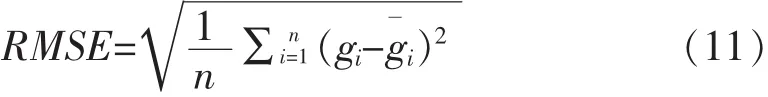
另外，为了详细比较两个算法最后填补的RMSE，所以我们增加一个评价量decrmse表示两种填补结果的差：

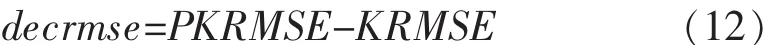
PKRMSE表示改进算法的均方根误差，KRMSE表示原KNN算法的均方根误差.因为RMSE在做评价标准时，数值越小，就代表估计值就越接近原始数值.所以当decrmse小于零时证明改进后的算法均方根误差更小，也就说明它的填补效果更好.文中将改进的算法称为PKNN算法.

实验的平台是Windows10专业版，Intel（R）Core（TM） i5-3210M CPU 2.5 GHz，4 GB 内存，500 GB 硬盘.开发工具采用matlab R2015a.选用UCI数据库上的 wine，slump，isolet，SPECTF.UCI数据库是一个专门用于测试机器学习、数据挖掘算法的公共数据库，库中的数据都有确定的分类，因此可以用均方根误差直观地表示缺失数据填补的效果，缺失比例取5%到60%，本次实验取K值分别为4、8、24，所以每组实验分三个部分，为避免实验偶然性，每次实验10次取均值.数据集信息如表1所示.

3.2 K为定值不同的数据集结果

对于上述数据集均取K值为24，观察改进的算法的填补效果，对比传统的K近邻填补算法，比较结果如图1至图3所示.

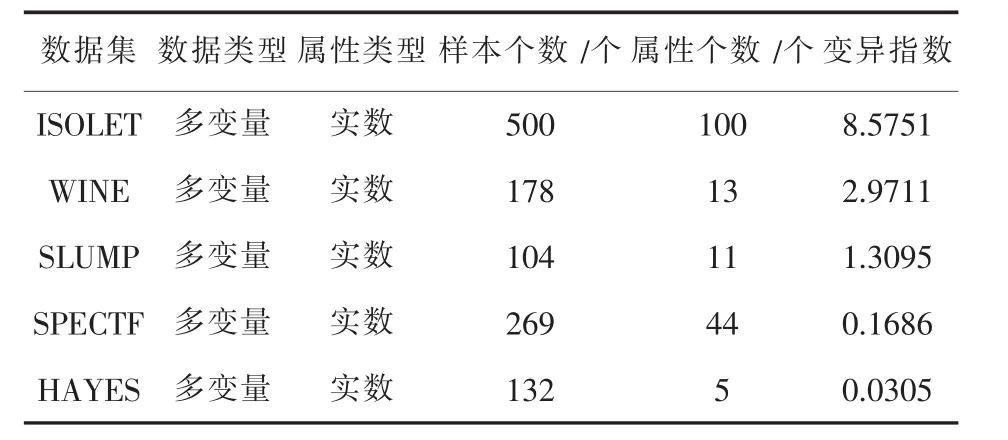
表1 实验数据集信息

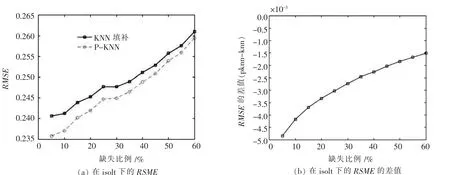
图1 ISOLET在K=24时填补效果

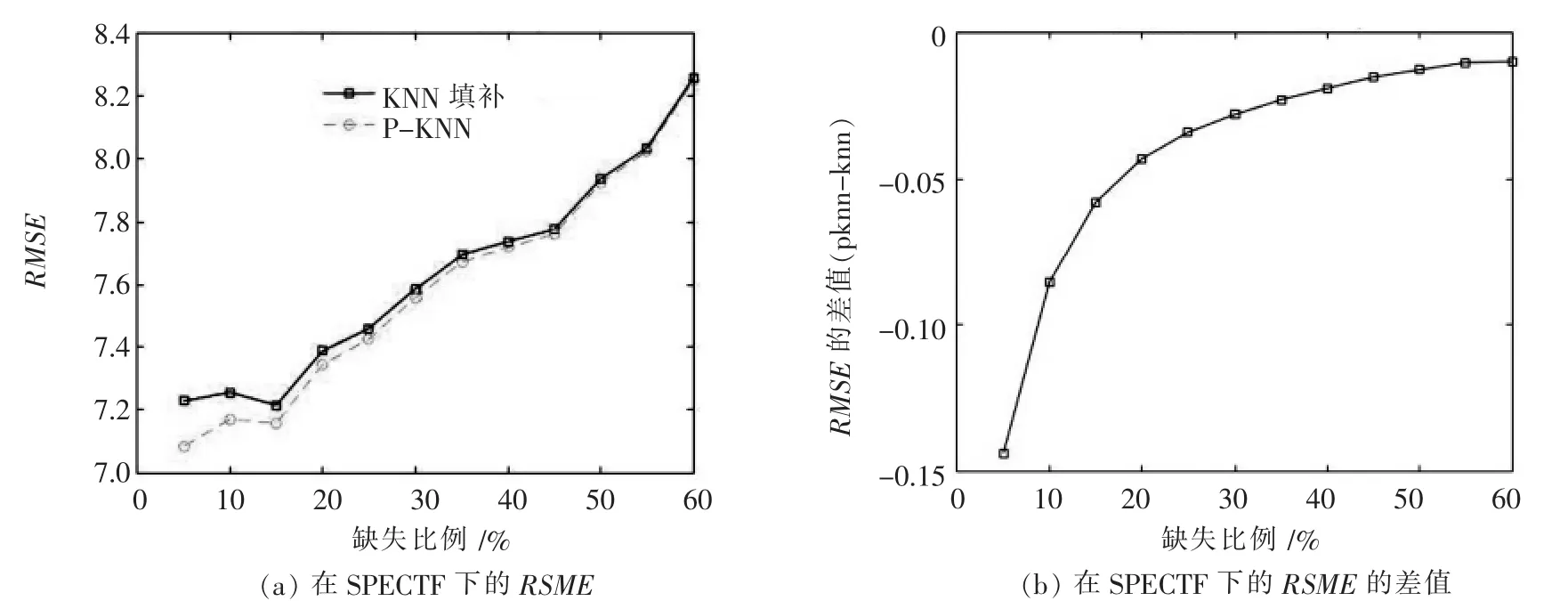
图2 SPECTF在K=24时填补效果

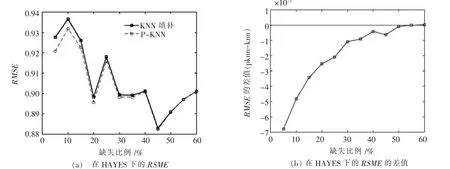
图3 HAYES在K=24时填补效果

对这3种数据仿真时，由实验结果可以看出，改进后的算法对缺失数据项的填补效果要比传统KNN填补算法填补效果更好，并且在数据缺失比例比较低时优化效果更明显，随着缺失比例上升，数据集中完备数据减少，可用信息量降低，改进算法结果逐渐接近传统填补算法.在另外两组数据组中，均方根误差数值较大，两条曲线很接近，但是从两者数值差值可以比较出仍然是改进过的算法拥有更好一些的效果，如图4所示.

3.3 不同K值对结果的影响

实验中，我们对K近邻的数量选取还做了不同实验，分别去了K值为 4、8、24，观测不同 K值下的结果，及改进的算法和K值的关系，其实验结果如图5所示.-3

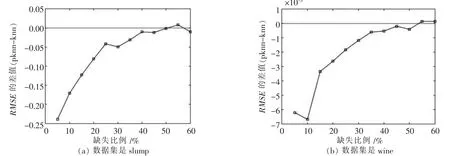
图4 SLUMP和WINE在K=24时填补效果

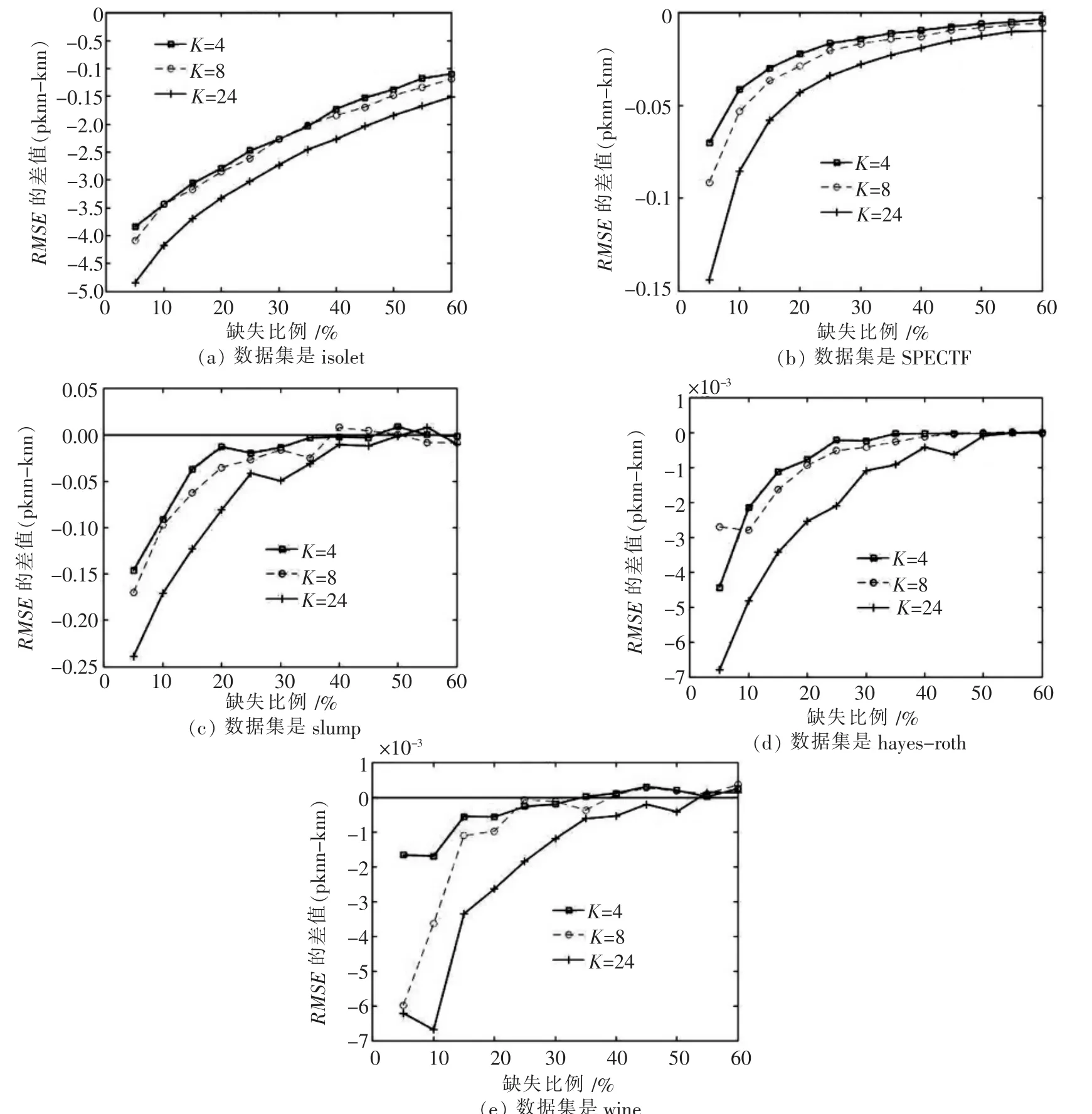
图5 不同数据集在不同K值的填补

由几组实验的结果可以看出，对于不同的K值，K近邻选择数量愈多，改进后的算法的填补效果明显也更好.三种K值时都有相同的趋势，随着缺失比例上升，逐渐趋于相同，且趋于0.证明缺失比例到一定程度后，K近邻的数量对填补的结果影响越来越小，并且可用信息量减少后，改进算法优化效果也不在明显.

3.4 与其它算法的比较

为了测试实验结果的准确性，和对算法改进的可行性，本次实验加入了列均值填补算法，来比较填补算法的效果.表2是在5个数据集上进行填补实验的均方根误差.其中：KNN表示传统的K近邻填补算法，P-KNN表示结合了属性相关值的K近邻填补算法，其后的数字表示K近邻选择的个数，比如，KNN_8表示近邻个数为8的经典KNN填补算法.col-means表示列均值填补算法.取缺失数据为10%时的实验数据.

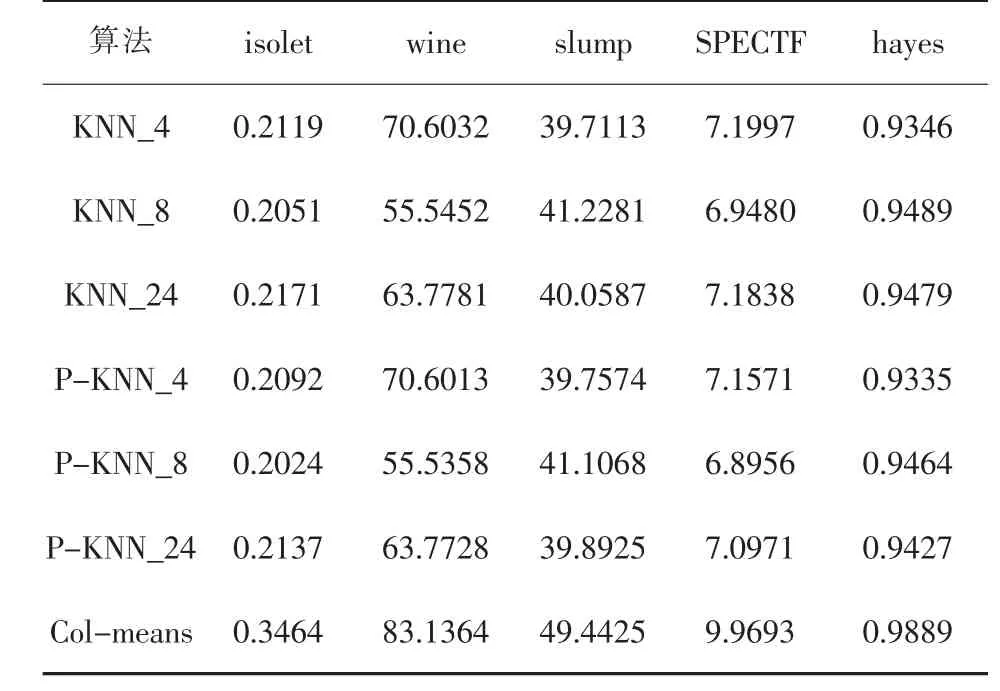
表2 三种算法均方根误差

从表2中数据可以看到，在5个数据集上，缺失比例保持在10%时，传统KNN算法和基于属性相关的KNN算法，在取近邻个数相同情况下，它们的误差基本上是保持相同的.而列均值填补算法在五种数据集上的误差都高于KNN和改进的KNN算法.这种情况的原因可能是：①缺失比例较低，数据完备性高，同一列数值更多，列均值计算的数值大，相关性较低的一些数值也被计算其中.②列均值对于异常点比较敏感，而KNN算法在选择K近邻时，近似性低的数据项不会被选择，因而排出了一些噪声数据的影响.

在不同缺失比例，五种数据集上我们也做了相同的实验，在K为24时，实验的结果是比较直接的，图6表示SPECTF、SLUMP和HAYES三种算法的效果图.

图6 SPECTF、SLUMP和HAYES三种算法比较

在SPECTF和HAYES数据的实验中，三种算法的结果折线图可以直观的展现出来，在SLUMP数据进行实验时，两种KNN算法仍然是基本上保持持平的，但是折线图不能很好的体现出来，这种情况的原因和同意维度下数据值的大小离散程度较大有关系，近邻算法的近邻数值相差不会太大，但是在列均值计算时，这些离散的数值会一同计算，从而影响了均值和紧邻计算均值相差较大.另外两组的实验数据结果如表3和表4所示.

类似的，从表3和表4中可以看出，依然是KNN的算法准确度要高于列均值算法.相较于经典KNN，经过属性相关度改进后的算法保持了一定的优化效果，不过，随着缺失比例的上升，准确度也有下降的趋势.但是列均值却没有这种情况，由于采用的是随机缺失的机制，对于整体而言，部分随机的数据，对于均值的影响就比较小.

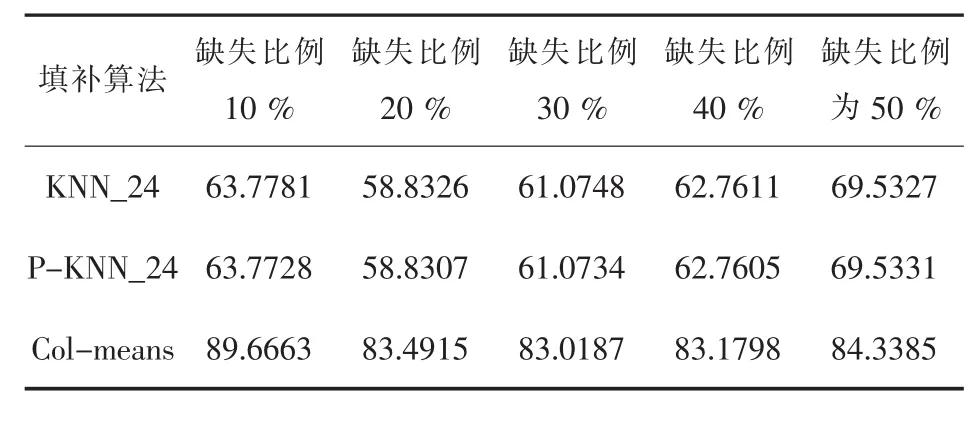
表3 wine均方根误差（K=24）

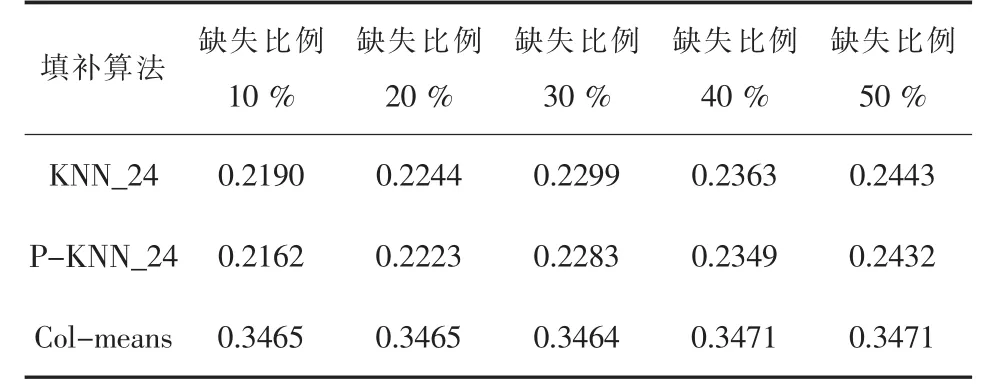
表4 isolet均方根误差（K=24）

4 结 论

通过PCA算法，使用相关系数来改进传统KNN填补算法，经过实验表明了它还是可取的.利用属性相关性计算属性相关量，尽可能的使用数据集中完备数据的信息来优化传统基于欧式距离的KNN近邻填补算法，获得了更好的结果，填补值更接近原始值，这样得到的数值也更贴近于实际获得的数据值.对于之后的数据挖掘和分析可以提供更好的数据组，最终结果也会更加准确可信.对于实验和改进算法中存在的不足，在后期的工作中我们会进一步改进和优化.