地铁网络可控性的研究

曾璐,杨杰,刘军,王莉

（1.江西理工大学，a.应用科学学院；b.电气工程与自动化学院，江西 赣州 341000；2.北京交通大学交通运输学院，北京100044）

0 引 言

地铁具有运量大、绿色、快捷等特点，已成为世界上城市的骨干交通方式.地铁的地理环境特殊、技术构成复杂、系统耦合性强、自然环境影响大等特征给轨道交通的运营安全提出了严峻的挑战.因此，地铁网络可控性研究对地铁的运输组织和规划具有重要意义.

迄今为止将复杂网络应用于地铁系统的研究已有不少，但是研究主要集中于复杂网络特性指标的研究.系统控制理论方面的研究不论是传统的控制理论还是现代控制理论都已经非常成熟[1].但是控制理论研究仅仅局限在系统控制，没有在网络方面加以应用.大规模系统的控制由早期的蜂拥控制过渡到持续多年的牵引控制.牵制控制是复杂网络控制方式的代表，汪小帆等[2-3]将牵引控制与蜂拥控制思想进行了结合研究；陈关荣[4]研究了牵制控制在复杂网络中的应用，有向复杂动态网络的能控性，以及“网络的网络”建模等内容．

Liu[5]研究了有向网络的能控性问题，首次将控制理论中的状态空间方程秩的判断运用到网络可控性当中，同时将有向网络转化为二分图并求出最大匹配．Liu的研究掀起了网络可控性研究的一个新的起点，为后续学者的研究奠定了基础．Yan[6]在Liu研究的基础上，从能量消耗的角度分析了不同类型网络的可控性与能量消耗关系．Nepusz[7]考虑了网络中连边上的动力学过程，将网络转化为以边为主体的模型．Ferrarini[8]将驱动节点的概念延伸到驱动边，指出节点是时变的，但是边通常是恒定的．Jia[9]利用随机抽样的方法计算出节点的控制能力，发现节点的控制能力由节点的入度决定，入度越大的节点越不容易成为驱动节点．

此外，席裕庚[10]运用了大系统控制理论的典型方法解决复杂网络的可控性，构建了 “系统—控制—信息（System-control-information,SCI）”的 分层结构．Lombardi[11]将可控矩阵应用于网络中，指出矩阵是从输入信号到节点的路径增益．Meng[12]研究了铁路列车服务网的可控性．基于列车服务网的免疫传播和级联失效定义了驱动节点，构建了改进的LB模型，研究了驱动节点搜索算法，提出了列车服务网的对偶图．在工控系统中，周克良等[13]基于可变论域模糊PID控制，设计了PLC控制的烘房智能温控系统，使系统输出响应达到稳定可控的状态．Ravindran[14]运用最大匹配算法识别驱动节点，并对其进行了分类，通过可控性分析识别癌症信号网络中的关键调控基因．研究发现主干驱动节点是癌症表型关键的因素．Li[15]对美国电网的拓扑结构和可控性进行了分析，提出了一种新的方法量化间歇节点成为驱动节点的概率．

目前网络可控性的研究基本上都是基于复杂网络，将网络可控性运用于实例少之又少．大部分的既有研究都是在复杂网络特性层面上，即便是运用于不同类型网络分析也是回归到网络特性指标的分析．

文中基于地铁网络结构特性的分析，在传统控制理论基础上构建了地铁网络可控模型．以北京地铁为例验证了地铁可控模型，并对三大城市北京、东京和广州的地铁网络进行了可控特性分析．期望通过改变驱动节点个数使得网络系统达到期望的状态，即整个地铁网络系统处在可控范围之内．

1 网络控制理论

1.1 系统可控

对于系统，希望通过对外界输入信号使得网络系统达到期望状态，或者适当的输入调整网络系统的性能，从而实现对网络的全面控制．但是实际当中由于复杂网络的系统规模庞大，传统的控制理论很难直接应用，单计算量就非常大，计算复杂度也非常高．而且大部分现实中的复杂网络系统都是非线性的，影响因素颇多，而且存在很多不稳定因素，因此实现全网的控制非常困难．

如果存在一个分段连续的输入u（t），能在有限时间区间[t0，tf]内，使系统由某一初始状态 x（t0），转移到指定的任意终端状态x（tf），则称此状态是能控的．若系统的所有状态都是能控的，则称系统是状态完全能控，简称系统能控．在控制理论中，线性时不变定常系统的输入-输出模型表示如公式（1）所示：

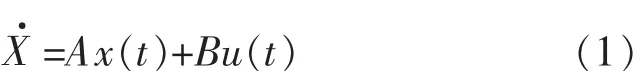
其中，x（t）是状态量即 x（t）=（x1（t），…，xN（t））T；

u（t）是输入信号即 u（t）（u1（t），…，uM（t））T，M≤N；

A 是状态矩阵，A∈RN×N；

B 是输入矩阵，B∈RN×M；

线性定常系统Σ（A，B）其状态完全可控的充要条件是由A、B构成的可控性判别矩阵满秩，即rank（C）=N；当 rank（C）＜N 时，系统为不可控．

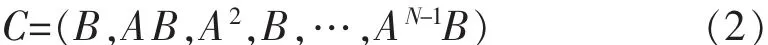
1.2 地铁网络可控模型

地铁系统是典型的复杂系统，系统结构及设备设施的复杂性使得系统的不稳定性增强．如果能对其可控，通过改变输入信号，可提高突发事件发生后应急处置效率．

地铁网络拓扑结构中，节点对应地铁车站，边对应车站之间的轨道交通线路．根据公式（1）在地铁网络建模，运用状态空间方程，可将公式（1）进行如下变换为：

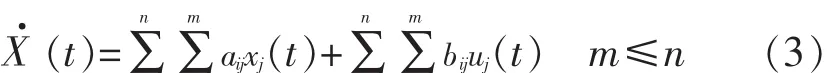
式（3）中：状态矩阵 A 的元素 aij，j为目的车站，i为起始车站，i和j为相邻车站．如果两个相邻车站之间有轨道相连，aij=1，否则aij=0；

xi（t）为 t时刻 j站的客流状态等级，根据车站内设施设备客流密度，将客流状态划分为4个等级；

bij为输入矩阵B的元素，如果i到j站有始发车则控制输入系数为1，否则为0；

uj（t）为第j个车站在 t时刻的存车量，存车量即有效时间内（未来一段时间）能够提供的运输能力.

1.3 网络结构可控优化理论

在网络控制中，Liu[5]提出了一种最少驱动节点ND的方法控制网络，仿真实验结果表明驱动节点的数量主要是由网络度分布决定的.稀疏的异质型网络往往更难控制，稠密的同质型网络则需要少数的驱动节点即可控制.稀疏性是指网络平均度远小于最大可能的连通度N（网络节点数目），比如地铁网络等.异质型网络不仅考虑网络的拓扑结构，而且还考虑网络中节点和边的内容属性信息.例如社交网络、微博网络、基因调控网络、电力网、语言概念网络等.

Liu[5]将网络结构可控与图论相结合，从边和点匹配的方法去判断一个网络是否可控.判断一个网络是否结构可控，必须具备以下三个前提条件.可控网络如图1所示.

1）线性控制系统（A，B）是结构可控的；

2）有向图（A，B）不包含不可达节点也不包含扩张结构；

3）有向图（A，B）由掌结构生成的.

在图 1 中，通过给定输入信号 u1，u2，u3，如果系统是可控的，输入信号可以通过所有的路径到达所有的节点.如何将不可控的网络转化为可控的网络，或者说如何确定一个网络的最少输入信号即驱动节点数量，这就转化为匹配问题了.二分图匹配点的方法，将网络中的各个节点进行匹配.匹配边是指任意两条有向边没有共同的顶点 （头或尾节点），匹配点是匹配边的头节点.

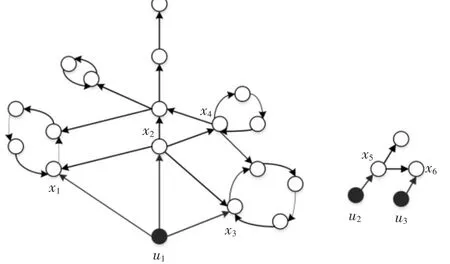
图1 可控网络

如果全网的所有边都没有共享头节点或尾节点，则称全网达到最大匹配，即ND＝1.假如没有完全匹配，驱动节点的值ND等于非匹配的节点数，如公式4所示.对非匹配的节点给定输入信号可达所有的匹配点即可控制全网，同时通过最大匹配法也可得到最少的驱动节点.

2 案例分析

2.1 典型地铁网可控性算例

截至2015年12月26日，北京地铁共有18条运营线路（包括17条地铁线路和1条机场线），去除未开通的车站拥有319座车站 （包括重复计算换乘站）.将该理论运用于整个北京地铁全网上，考虑双方向的通车情况，即一条线车的通行是双向的.为了方便计算，构建一个基础数据库，具体如图2所示.

对全网上的每一个车站按线进行编号，例如1号线：苹果园 0101，古城 0102，八角游乐园 0103，八宝山 0104，玉泉路 0105，五棵松 0106，…；2号线：西直门0201，车公庄0202，阜城门0203，….车站编号的前两位是线路编号，后两位是这个车站所在线路的编号，如表1所示.区间构成的矩阵即为状态矩阵A，始发车即为输入矩阵B.根据地铁的拓扑图可以知道构成的A矩阵必定是稀疏矩阵.

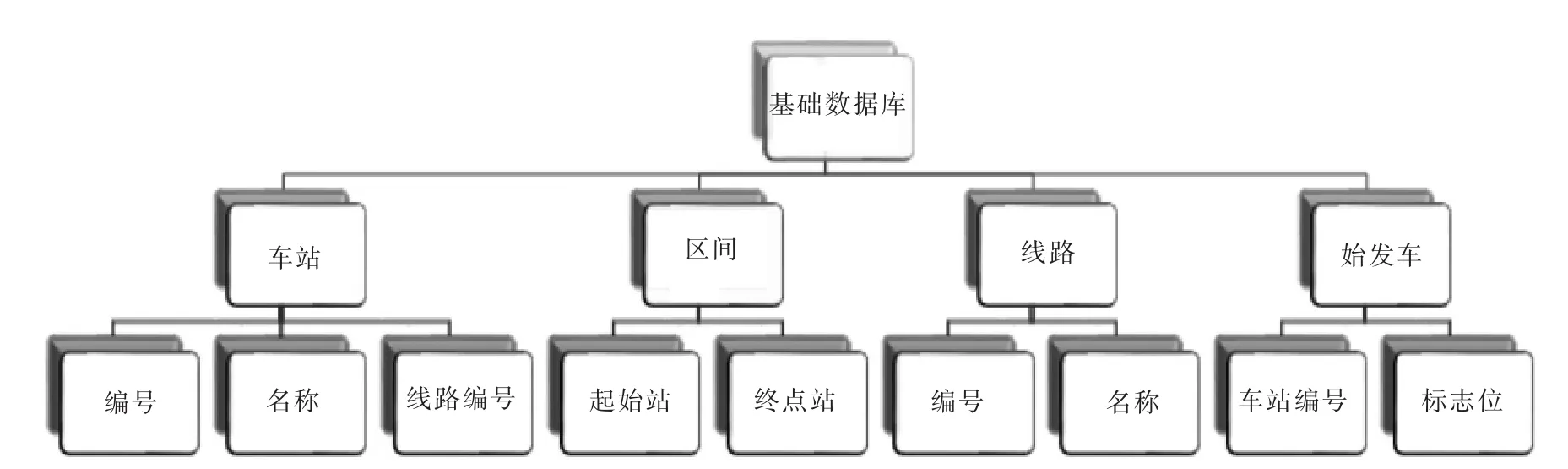
图2 基础数据库

节点与节点之间的边是有向的，方向为车的行驶方向，则全网是双向网络.依据区间基础数据，运用邻接矩阵性质解析可得到状态矩阵A为一个由0和1构成的319*319矩阵：

B矩阵由始发车站构成的输入矩阵，所谓的始发车站即从车辆段发出的空车到本站上人.通过北京地铁各线行车情况数据及时刻表可获得各线始发车具体如表1所示.B矩阵即变换为一个由0和1构成的319*51的矩阵：

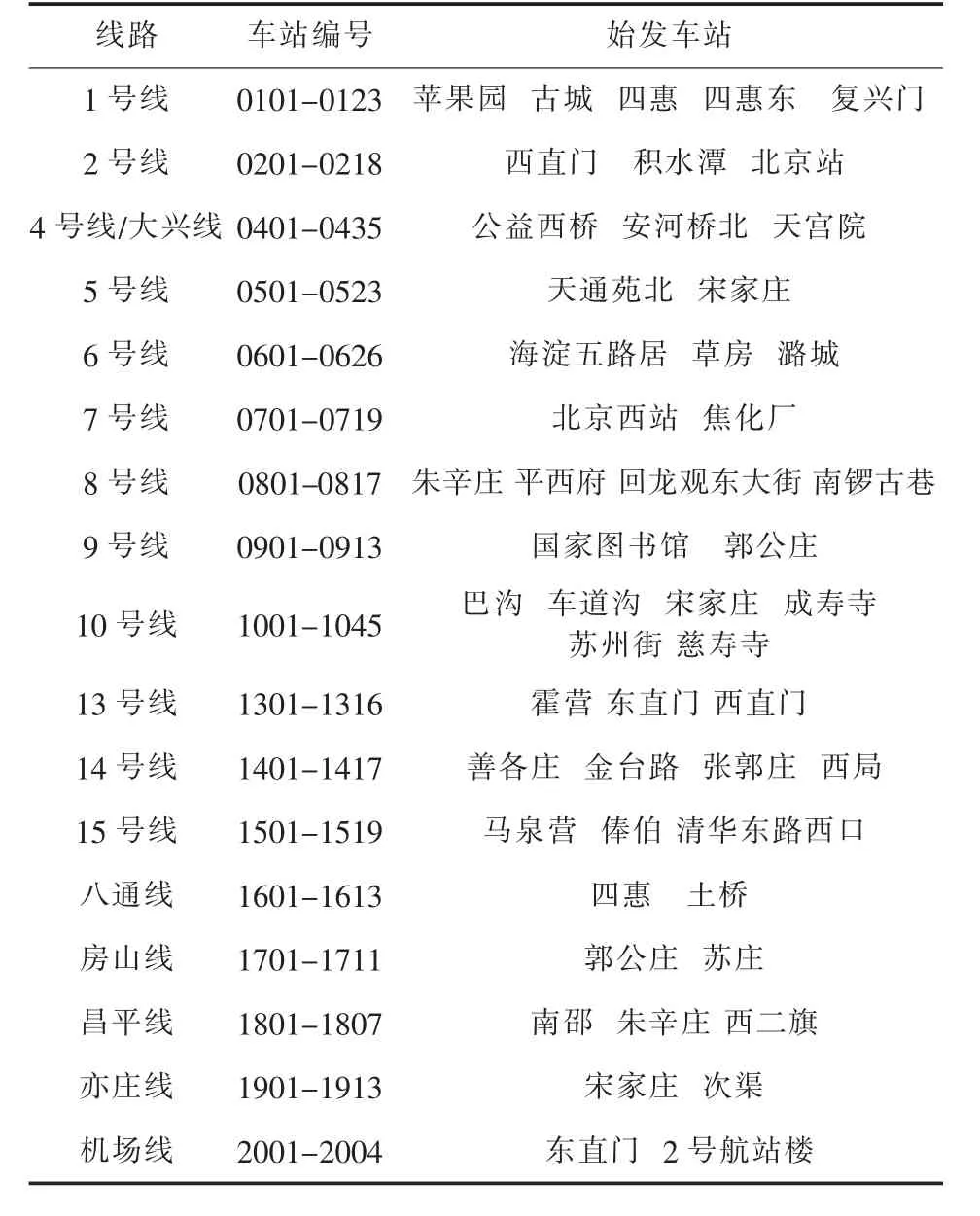
表1 北京市轨道交通路网各线路、车站编号、始发车站

根据北京市2015年12月实际运营线路图，建立如图3所示的北京地铁驱动节点网络拓扑图.图3中黑色的圆圈代表驱动节点车站即始发车站.通过计算可得，rank C=68，说明系统是不可控的.

图3 基于驱动节点的北京地铁网络拓扑

此外，还对广州地铁做了同样的可控性验证.截止到2016年4月，广州地铁车站去除未开通及APM线（包括重复计算换乘站）共有160个.通过基础数据解析可得到控制矩阵C，计算可得rank C=37，整个广州地铁网络也是不可控的.

地铁网不同于其它的网络，它存在数量较多的换乘站点.换乘节点至少是由两条线路交叉，甚至更多的线路交错在一起.根据最大匹配理论，换乘站节点周围不匹配节点较多，驱动节点数量不够，所以网络不可控.

2.2 典型地铁网络可控特性分析

在世界地铁系统中，北京地铁运营规模居世界之首.截止到2015年，年客运量已经达到32.5亿人次.日本东京，是全亚洲最早的地铁线路城市.目前包括由都营地下铁、东京地下铁两家公司共同营运的总共13条线路.截止到2016年4月共有287个车站（重复计算），运营里程达到304.1 km，日平均运量约850万人次.广州地铁是我国第四个开通并运营地铁的城市.截至2016年4月，广州地铁共有9条运营路线，总长为260.5 km，共172座车站（重复计算）.

在拓扑结构和运输组织方式上，东京地铁相对比较复杂，北京地铁相对规范，广州地铁较为简单.通过三大地铁的数据查询以及列车时刻表，可得到它们的网络拓扑结构信息及始发车站信息.基于驱动节点的定义，三大城市地铁的车站数量（不包括重复计算）、驱动节点数和边数如图4所示.数量是最少的，但是驱动节点比重却最大.这是由于广州地铁不存在环线，主要是呈现放射状态，换乘站较少，节点的度数及聚类系数都比较低，因此相对比较稀疏.但是越稀疏的网络所需的驱动节点数目相对较多.

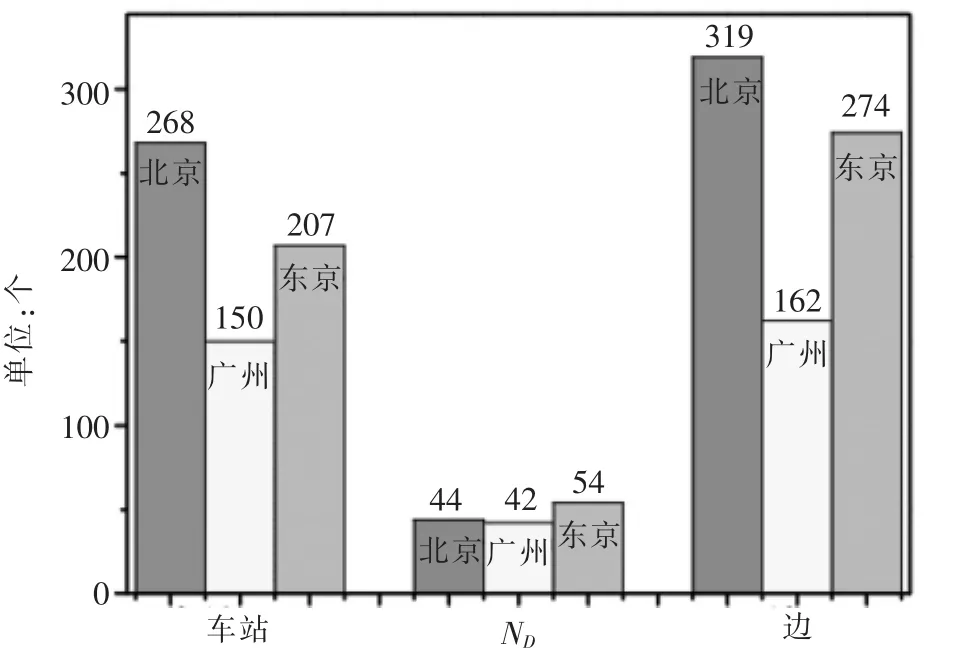
图4 三大城市地铁指标对比

北京与东京相比，东京的节点数小于北京，但是驱动节点所占的比重却大于北京.这是因为东京的线网结构复杂于北京，其存在多种列车开行方案及运输组织方式，采用的是迂回线路，灵活性较强.三大城市地铁驱动节点度k的度分布p（k）如图6所示.

东京地铁的网络拓扑结构呈现的是放射环状结构，将环线和放射线相结合，避免了客流过度集中，增强了整个网络的连通性.另外，从运行计划及时刻表发现，东京地铁的运输组织方式融合了周期化列车运行，直通运行及快慢车混合运行的多种运营方式.

北京地铁的网络拓扑结构依据北京城市规划的分布，地铁线网结构是以天安门为中心向四周扩散，环线也是较为方正.城区线网呈现棋盘状，线路末端呈放射状.我国地铁列车速度较为单一、列车间越行及跨线的机会较少.

广州地铁的网络拓扑结构主要由“交通疏导型”和“规划引导型”线路构成，至今没有环线线路，形成的是既向心又交织的线网结构.

大多数实际存在的大型网络通常都具有稀疏性，根据稀疏型网络的定义可知地铁网络属于稀疏型网络.三大城市的驱动节点占节点总数百分比的对比图如图5所示.

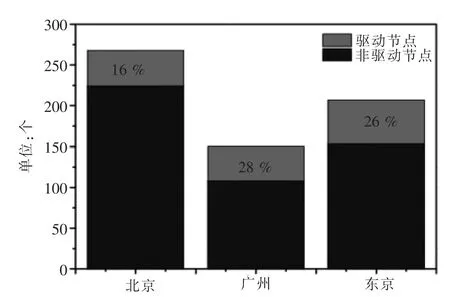
图5 三大城市驱动节点与节点对比

从图5中可得出，驱动节点占所有节点比率最高的是广州，然后依次是东京和北京.北京与广州相比，节点数北京是最多的，但是驱动节点占节点比重是最少的.地铁实际线网结构中广州的节点

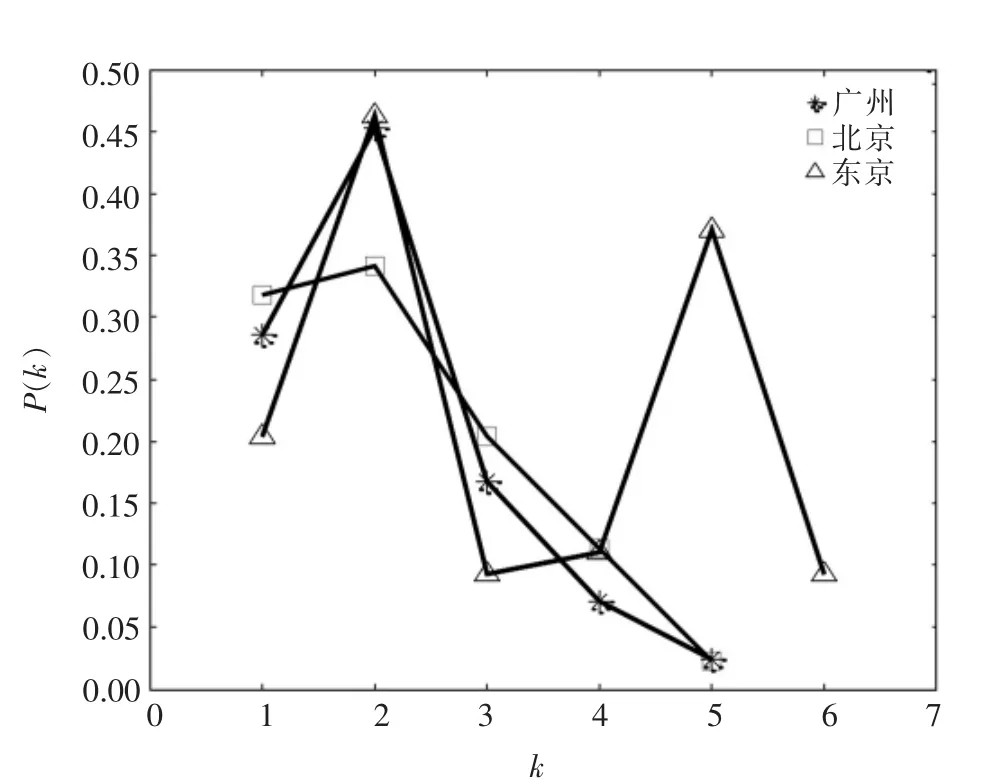
图6 三大城市地铁度分布

图6 中，北京地铁网车站数是最多的，线网规划结构属棋盘状，线路横平竖直，基本沿着大的城市干道，经过了主要的城市重要建筑和场所，整体来说较为规整.驱动节点及换乘站点的度数较为平均，其驱动节点的度分布呈现幂律度分布.以上分析可以得出，有向网络中需要施加的外界输入的节点即驱动节点的个数与该网络的度分布有关.

3 结 论

本文主要从网络可控的角度研究了地铁网络的可控性，并结合实例分析了其特点.具体得出结论如下：

1）构建了地铁网络拓扑结构，依据结构可控模型，以北京地铁为例验证了网络可控性理论.比较了不同结构的地铁网，从复杂网络的特性指标及可控的角度分析了它们的结构可控特点.

2）通过对地铁网络可控性的分析，结果表明地铁物理网在现行条件下是不可控的.因此当突发事件发生时，地铁的应急效率相对较低，在应急管理方面通常依赖公交等其它交通方式接驳.

3）通过对典型地铁网络可控特性分析，相对于广州、东京，北京的驱动节点占所有节点的百分比略低.从网络可控性角度，建议北京地铁增加驱动节点数量，提高其可控性，改进目前运输组织策略.

以上分析只是局限在物理网的架构下，在下一步的研究中打算将客流加载在当前的地铁网络上，将客流和列车服务相结合，实现真正意义上的运能协调及控制.