基于爬坡换道的驾驶特性分析
姜 康, 申梦婷, 黄志鹏
(合肥工业大学,汽车与交通工程学院,安徽 合肥 230009)
0 引 言
我国道路建设初期规划与设计理论尚不成熟、建设资金不足,造成现有公路网中存在一些不完善的道路,如道路线形不良、安全设施设置不当、交通管理措施不够合理等。其中道路线形不良的一个主要原因是受地形地貌等因素限制,长大纵坡较多,这些路段往往是道路交通事故的易发多发路段[1]。
目前国内外已有较多关于坡道道路的研究,使用的大多是元胞自动机(cellular automata,CA)模型[2-6];朱海明等[7]从车辆动力学入手, 对NS模型进行改进使其适用于弯路和坡路;樊艳红[8]针对限速区、弯道等特殊路段,建立CA模型,研究复杂路况下各种非线性现象及交通事故概率问题;梁国华等[9]通过引入纵坡坡度等参数改进了CA模型中的加速与慢化规则,同时考虑换道规则,构建适用于坡道路段的模型。此外,针对坡道对货车行驶影响的研究也已经趋于全面,庄传仪[10]研究了载重车在上坡行驶时,纵坡坡度与车辆行驶速度随波长的变化规律,并绘制出载重汽车的爬坡性能曲线;梁永东[11]研究了高速公路爬坡车道设置的相关问题,并着重分析了爬坡路段上大型车的运行特性;钱静[12]针对大型车在高速公路爬坡路段交通安全影响机理进行了相关研究。
在实际行驶过程中,除了不规则路段会对交通流产生影响,车辆类型、载重质量以及驾驶员的特性也都是不可忽视的因素[13-14],尤其是驾驶员特性。但现有的研究往往忽略了不同性格驾驶员的行车特性,致使分析结果不够全面、准确。而且,对于坡道仿真的CA模型仍存在不足,如元胞尺寸划分过大,未能充分考虑车辆在坡道路段的加减速性能,单车道模型不符合实际道路状况等。
鉴于此,笔者在细化元胞单位长度的基础上,将驾驶员分为激进型与谨慎型两类,分析其驾驶特性,并利用爬坡路段纵坡度改进CA模型。通过仿真交通流在爬坡路段的运行状况,对比爬坡换道与平直路段换道的差异性,分析坡道纵坡度对两种类型驾驶员的影响。为简化计算,道路上所有车辆都为货车,不做混合车型的交通流驾驶特性分析。
1 爬坡路段交通流运行特性及影响因素分析
1.1 影响因素分析
1.1.1 驾驶行为
道路上由各种类型的车辆混合组成,根据车辆驾驶员行为可将其分为谨慎型、稳健型与激进型3类[15](在下文中,统一将谨慎型驾驶员驾驶的车辆简称为谨慎型车辆,激进型驾驶员驾驶的车辆简称为激进型车辆)。当3种类型的车辆在爬坡路段上混合比例行驶时,车速降低不等,易造成较大的速度差,使换道、超车需求増加,加减速频率増大,驾驶行为频繁改变,导致坡道路段交通流发生紊乱。实际行驶过程中,爬坡路段交通流主要受谨慎型与激进型这两类车辆的影响,稳健型可忽略不计。
1.1.2 坡道纵坡度
车辆的爬坡能力会受动力性能、道路条件等因素影响,从而产生速度折减现象;坡道纵坡度对车辆的影响也会因驾驶员的驾驶行为的差异而有所不同,同时也会因车辆类型不同而产生不同的影响。总体来说,在爬坡路段,车辆运行速度的下降幅度随纵坡坡度的增大而增加[16]。
1.2 交通流特征分析
1.2.1 交通量
车辆在平坡段行驶时,交通量基本维持平衡状态,当逐渐驶入上坡段时,交通量以微小幅度减小,当车辆行驶至竖曲线段时,激进型车辆车速降低至其所能容忍的最低车速后,不断加速寻找可换道、超车间隙,进而导致交通量有所上升。
1.2.2 车 速
谨慎型车辆在爬坡路段的平均运行速度比激进型车辆降低地快,且道路上车速离散性较大。在交通量増大的情况下,若谨慎型车辆长时间低速占道行驶,易导致跟驰车辆的不合理驾驶行为,加剧安全隐患。
2 爬坡路段CA模型建立
2.1 随机延迟概率的确定
在实际交通中,激进型与谨慎型车辆对前车敏感驾驶的随机延迟概率是不同的,一般谨慎型车辆的随机延迟概率要比激进型的延迟概率大。针对这两类车辆的差异性,分别引入不同的随机延迟概率,同时考虑车间距、车速对随机延迟概率的影响[17],具体表现为
1)当前车变慢、跟随车速预期大于车间距时,谨慎型车辆为了避免碰撞常处于减速状态,并以较大的概率Pb随机减速;
2)当跟随车速预期等于车间距时,将有一部分车辆处于跟随状态保持车流平稳,而另一部分车辆为了保证安全行驶,将以概率Pf延缓车速;
3)当跟随车速预期小于车间距时将加速行驶,只有很小一部分车辆以概率Pa延缓加速。
其中,Pa 伴随着不同的驾驶行为特性,驾驶员可以根据周围车辆的车速、车距等参数的变化,随时更改自身驾驶行为,因此,城市交通流中常出现车辆拥堵、排队、变换车道等行为[18-20]。在进行换道行为时,驾驶员一般会遵循一定的换道规则[21],笔者针对驾驶员换道特性,分别对激进型与谨慎型车辆引入相应的换道规则[22]。 2.2.1 激进型驾驶员的换道规则 (1) 2.2.2 谨慎型驾驶员的换道规则 (2) 式中:vi(t)为第i辆车在t时刻的速度;di,n(t)、di,b(t)表示在t时刻第i辆车与邻道上相邻前、后车之间空的元胞数;ds为安全距离;vA、vC分别表示激进型与谨慎型车辆的最大速度;rand()是产生0~1之间的一个随机数;Pch为驾驶员的随机换道概率;Ti=0,1分别表示第i辆车是谨慎型与激进型车辆。 坡度对货车的影响主要是在上坡与下坡过程中,由于坡道纵坡度的存在,重力加速度g对车辆的加、减速度会产生影响。在爬坡过程中,重力在沿纵坡的方向分量对货车起到了减速作用,其加速度为gsinα,α为坡道倾斜角[23]。货车在坡道路段的受力分析如图1。一般城市道路的纵坡度τ较小,为简化计算令sinα≈tanα≈τ。 图1 货车在爬坡路段的受力分析Fig. 1 Force analysis diagram ofthe truck on climbing section 坡道对货车的主要影响体现在车辆上坡时的加速度αu和减速度βd,当车辆处于坡道路段时,这两个参数会发生变化: (3) 式中:α、β为车辆在平直路段的最大加、减速度。 在建模时,谨慎型与激进型车辆的演化规则都是基于FI模型[25-26]进行改进的,记xi(t)为第i辆车在t时刻的位置,gapi(t)=xi+1(t)-xi(t)-l表示在t时刻,第i辆车与前方紧邻车辆i+1的间距,l为车辆长度。改进后的演化规则为 1)确定换道规则:按照公式(1)以及公式(2)进行换道; 2)确定随机延迟概率p: 3)加速过程:为满足驾驶员对于更高车速的期望,车辆进行加速行驶: vi(t+1)=min{gapi(t),vmax,vi(t)+α}; 4)随机减速过程(以概率p):车间距小于最大车速时,为了保证安全驾驶,该车辆进行减速。考虑到驾驶员驾驶行为的不确定性,在规则中引入随机慢化概率p,行驶的车辆按照随机慢化概率进行速度上的慢化,即: 若gapi(t) 5)位置更新:xi(t+1)=xi(t)+vi(t+1)。 仿真时,车道由双车道组成,每条车道有10 000个元胞,长度为5 km;含坡道路段仿真中,坡道长度500 m,坡度为τ。时间步长取1 s,采用周期性边界条件。记N为分布在道路L上的车辆数;vA、vC分别为激进型和谨慎型驾驶员所驾驶车辆的最大车速;pA、pC分别为其随机延迟概率。初始时,道路上由激进型与谨慎型两种类型驾驶员组成,所占比例分别为ρA,ρC,且ρA+ρC=1,谨慎型车辆占总数的λ(0≤λ≤1),换道安全距离ds=37.5 m。 表1 模型参数取值Table 1 Values of model parameters 为消除初始状态随机性对结果的影响,模型每次运行16 000时步,取最后6 000步进行计算,得到每一次运行的平均速度,然后再对30个样本取平均。 3.1.1 单车道 图2是谨慎型车辆占比50%、80%时,纵坡度分别为5%与15%时的车辆平均速度对比图。当密度小于0.3时,4种组合的最大车速都只能达到5左右,这是因为在单车道上只要有谨慎型车辆存在,跟驰车辆的速度都受限于前方谨慎型车辆的最大行驶速度。随着坡度增大,坡道对车辆行驶的阻碍增大,道路平均速度下降速度加快。 图2 单车道仿真基本图Fig. 2 Basic diagram of single lane simulation 3.1.2 双车道 在单车道时,因跟驰车辆受前方慢速车的限制,且无法换道,当道路车辆密度达到一定值时,就会造成交通堵塞,车速为0,但这与实际道路情况并不相符。因此,对模型添加换道规则后,进行双车道仿真分析,得到结果如图3~图4。 图3 不同坡度,λ不同时,密度-流量Fig. 3 Density-flow contrast with different slopes and λ 图3为谨慎型驾驶员占比30%、50%、70%时,不同坡度下的密度-流量图。随着密度的逐渐增大,道路流量也一直在增长,从图3可以看出,当坡度为5%,密度为1时,谨慎型车辆仅占30%时的道路流量最大,达到6.1,这是因为激进型车辆较多,平均车速较快,行使自由度较大;当谨慎型车辆逐渐增多时,谨慎型驾驶员为了行车安全,选择低速行驶,且轻易不换道,这就极易造成后方车辆车速无法提高,致使整条道路的平均车速较低,道路流量逐渐降低到5.5。对比同一混合比例情况下不同坡度对流量的影响发现,坡度15%时的流量比坡度5%时的流量降低0.7左右,随着坡度增大,行驶车辆爬坡性能受到影响,为保障道路安全,车辆被迫减速,驾驶员降低驾驶行为的改变频率,流量随之减少, 图4 不同坡度,λ不同时,密度-速度Fig. 4 Density-velocity contrast with different slopes and λ 图4为谨慎型驾驶员占比30%、50%、70%时,不同坡度下的密度-速度变化图。当密度为1时,平均车速最低为5.1,即没有造成完全堵塞状态,这是因为在双车道上行驶时,激进型车辆若受到前方慢速车限制时,会选择换道以达到理想的速度要求。当密度小于0.5时,随着坡度逐渐增大,速度变化开始变得明显,且坡度越大,速度降低越快。 同坡度下,将两种类型车辆不同混合比例下(30%,50%,70%)的速度变化进行对比,可以看出随着谨慎型车辆逐渐占据整条车道时,因其车速较低,换道条件不满足,跟驰车辆无法经常换道以提升行驶速度,自由流车速最大也只能达到谨慎型车辆的最大速度,车速变化趋于平缓。当坡度增加到15%时,平均车速最大值为5.6,比坡度为5%时的速度低,这是因为坡度过大,无论是谨慎型还是激进型车辆,坡道纵坡度对其限制作用都很明显,驾驶员为保证安全行驶,基本不采取变道或加速行为。同时,在爬坡过程中,激进型车辆的速度比谨慎型下降更快,这与驾驶员的驾驶行为有关,激进型驾驶员因追求高速行驶,速度波动更为明显。 图5、图6模拟的是ρ=0.37时的时空图,黑色表示速度为零、堵塞的车辆,灰色表示运动的车辆,颜色越深表示车辆的速度越小,白色代表空白区域。 图5 ρ=0.37,τ=5%时,系统的时空演化斑图Fig. 5 Spatiotemporal evolution patterns of system whenρ=0.37 and τ=5% 当坡度为5%,谨慎型车辆占比30%时,对比左右车道的时空图可以发现,左车道的空白区域比右车道多,车道使用率较低,但右车道的平均车速明显低于左车道,且在位置6 000~8 000,时间步8 000~10 000之间出现了小范围堵塞区域,车速为0,这说明大部分谨慎型车辆靠右车道行驶,阻碍了后方激进型车辆的提速。当谨慎型车辆占比增大至70%时,左右车道的利用率相差不大,大部分车辆都处于运行状态,激进型车辆受谨慎型车辆的车速限制,不断寻找换道机会,但因谨慎型车辆数过多,换道机会较少,被迫跟驰,尽管未造成明显堵塞区域,但车道平均车速整体小于谨慎型车辆占比30%时的车速。 图6 ρ=0.37,τ=15%时,时空演化斑图Fig. 6 Spatiotemporal evolution patterns of system whenρ=0.37 and τ=15% 当坡度增加到15%,谨慎型车辆占比30%时,右车道的空白区域较左车道多,且低速行驶的车辆也较多;当车道逐渐被谨慎型车辆占据时,激进型车辆为避免车速过低,大多偏左车道行驶,因此左车道的利用率较高。但左右两车道都在位置7 000~8 000的时候产生了延迟堆积,这是由于坡度过大,对谨慎型以及激进型车辆都产生了较为严重地限制作用,在爬坡过程中,车辆低速行驶,且不轻易换道,因此造成点阵拥堵现象。 仿真分析时,设坡道路段总长500 m,对比爬坡换道与平直路段换道的差异性得到如图7的结果(谨慎型车辆占比50%)。 图7 爬坡路段与平直路段的换道率Fig. 7 Lane changing rate of climbing section and straight section 从图7中可以看出,在密度低于0.2时,平直路段(i=0%)与坡道路段的车辆换道率均不断增加,其中平直路段换道率的增长速度明显高于坡道路段;在密度达到0.2附近时,平直路段的换道率达到最高值1.08,坡道路段的换道率接近最大值0.65,仅达到平直路段的一半左右,这是因为坡度限制了车辆的加、减速性能,且在爬坡过程中,驾驶员会减少换道次数以保障安全;当密度大于0.2时,平直路段的换道率开始下降,但坡道路段的换道率还会以较小的频率继续增长一段至最大值,随后持续下降,此时,由于在坡道前半段时,激进型车辆还未明显感受到坡度对车速的限制,仍会继续换道以达到自己理想的车速。当坡度为5%时,车辆换道率介于平直路段与坡度15%之间;当密度大于0.3时,随着坡度的增加,换道率下降速度越来越快,即使是激进型车辆也不会过度换道来追求速度。 道路特殊路段对交通流有着重要影响,笔者在分析道路坡道对货车影响的基础上,引入纵坡度,建立改进的FI模型,研究分析了道路纵坡度对不同类型车辆交通流特性的影响,以及车辆在平直路段与爬坡路段的换道差异性。通过仿真分析可以发现, 当密度小于0.5时,随着坡度逐渐增大,速度变化开始变得明显,且坡度越大,速度降低越快;同时,坡度对两类驾驶员的影响各有不同,谨慎型驾驶员在爬坡时的平均速度明显低于激进型驾驶员,当坡度小于5%时对激进型驾驶员的限制作用不甚明显,且谨慎型车辆的占比数量对道路整体的平均速度有显著影响,占比越大,平均车速越低,流量越小。当密度达到0.3时,道路上车辆换道率发生明显变化,显著降低,且坡度越大,换道率越低。笔者提出的改进模型能更好的反映出不同类型驾驶员的驾驶特性,模拟得到的交通流密度、速度与流量也更符合实际。2.2 换道规则
2.3 坡道纵坡度对货车运行的影响

2.4 改进的FI模型演化规则

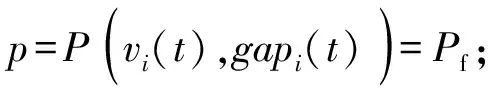
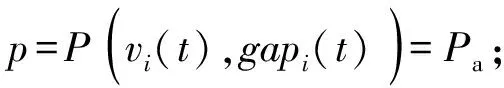
3 仿真分析

3.1 基本图



3.2 时空图


3.3 爬坡换道与平直路段换道的差异性

4 结 语

