外来资本竞争如何影响地区生产率?
——基于门槛效应的经验研究
胡浩然
一、引言
40年以来中国经济快速增长,国内生产总值(GDP)年均增长率保持在10%左右,创造了人类历史上的经济奇迹。但是中国地区经济发展不均衡,发展水平表现出东、中、西部地区梯次降低,处于相同地区的不同省份的经济发展水平存在很大差异,地区经济发展的不平衡越来越制约中国经济发展。而造成这一现象的原因,除了各省份的初始禀赋和发展水平差异外,和各省份和地方政府的激烈竞争密切相关(付强和乔岳,2011[1]),其中地区竞争的核心是资本竞争(贾莎和郑法川,2014[2]),特别是外方投资因素(韩超和王海,2014[3])。地区经济发展水平的差异在微观层面上可以表现为产业生产率的差异,中国地区经济差异与生产率为代表的产业竞争力差异的变动趋势基本相同,生产率差异是造成各省份经济差异的主要原因(石风光和李宗植,2009[4])。1994年以后财政分权改革的结果是使得地方政府获得适当的税政管理权和相对独立的利益,加剧了地区间的竞争,包括引进外资(FDI)竞争(周黎安,2004[5])。可以认为,地方政府为了赢得更好的发展机会,彼此之间都有激烈竞争,竞争对象包括吸引优质项目和发展所用到的资本,特别是在资本积累初期,FDI成为资本积累的重要来源。本文以生产率作为衡量地区经济发展水平的微观层面指标,主要研究外商投资衡量的资本竞争对地区生产率的影响。但是经济发展中,资本由最开始的稀缺,到后来的富足,甚至超出了当地经济所需的资本积累,那么,继续引进外资的作用将如何变化?因此,我们有必要研究资本积累过程中引进外资对地区产业生产率提升作用是否存在门槛,进而判断处于不同经济发展阶段的各省份对于招商引资可以采取怎样的应对策略。
本文主要使用2002—2011年省级面板数据,并且加入了二位数行业数据。我们使用宏观层面数据,DEA-Malmquist方法可以很好地解决样本选择和共时性问题,同时可以避免OP法和LP法测算的数据缺陷,因此,我们以DEA-Malmquist方法测算生产率。我们使用Gregory和Hansen(1996)[6]面板门槛模型来评估外来资本竞争对地区产业生产率提升作用的门槛效应,并且使用混合回归OLS模型作为基本的实证检验。我们研究发现:一是以引进外资衡量的资本竞争可以显著提高地区产业的生产率。二是考虑到地区资本禀赋存在异质性,我们发现资本竞争影响下对生产率的提升作用存在显著的三门槛效应。即在较高资本禀赋的地区,资本竞争对生产率的影响变得不显著,在较低资本禀赋的地区,资本竞争却能更好地提升产业生产率。本文认为,财政放权后各省份为了发展经济而积极地引进外资,官员晋升锦标赛使得竞争加剧,竞争的结果是地区经济的快速增长,但是,资本竞争应该考虑到地区的资本积累情况和经济发展的不同阶段。对于欠发达省份,资本积累还未完成,地方政府还应当大力引进外资,进而促进地区生产率和经济的提升,对于沿海发达省份,更应该注重利用本地资本和引进高质量的外资,盲目引进外资整体上可能对经济的提升作用不大,这和经济发展水平较高有关。
我们参阅了大量文献,可能依然存在不足,本文边际贡献在于:第一,大量研究都涉及外资对中国经济发展的作用,甚至有学者认为中国经济的成功依赖于FDI政策(Lall,2000[7])。但是已有研究较少将引进外资与资本积累联系起来,我们认为资本禀赋变化可能使得引进外资的作用减弱,进而使得资本禀赋和经济发展水平高的地区资本竞争变得低效或者无效。第二,我们发现引进外资对生产率的提升作用存在门槛效应,这对于地区间的外资策略和竞争策略的制定和实施都有现实意义。
下文结构安排:第二部分为文献综述;第三部分为理论模型、数据和变量说明;第四部分为全要素生产率的测算;第五部分为实证检验;第六部分是结论与政策建议。
二、文献综述
资本竞争显著存在并且对于中国经济增长具有促进作用。贾莎和郑法川(2014)[2]研究发现地方政府存在显著的资本竞争。韩超和王海(2014)[3]研究认为地区竞争增大了地区的资本积累,其核心是资本竞争,而FDI作为外来资本,更易于受到地方政府的青睐。已有研究认为外商投资是拉动中国经济增长的主要动力,促进了中国产业结构升级(郭克莎,2000[8]),有助于资源的优化配置,并且促进了经济发展(卢荻,2003[9])。在微观层面上,外资等资本积累影响了高新技术产业空间布局,缓解了融资约束(吴飞飞和邱斌,2015[10]),推动了内资企业技术水平提升(李晓钟和王倩倩,2014[11]),存在促进生产率的溢出效应(黄烨菁,2006[12])。中国经济的成功长期以来依赖于FDI政策(Lall,2000[7]),并且,外商投资促进经济集聚会影响当期地方政府的FDI政策,并且将影响后期的集聚效应的持续或消失,FDI带来的经济集聚效应和政策扶持之间形成了无穷尽的相互促进作用(向永辉,2013[13])。相反地,邓金钱和何爱平(2017)[14]认为引进外资进入城镇和非农产业集聚进而造成城乡收入差距增大。
考虑到在财政分权后和官员晋升压力下,地方政府的竞争加剧,长期以来GDP是衡量官员晋升的重要标准,其出发点是为了调动地方政府的竞争意识[注]1994年中国实施分税改革的财政分权化体制,并且在1998年发布了《党政领导干部考核工作暂行规定》,从而初步确立了政绩考核与晋升制度,地方政府逐渐形成以GDP为核心的晋升竞争制度。。有研究表明省级领导职务升迁和该省的经济表现呈正相关关系(江飞涛等,2012[15]),并且地方政府的竞争显著地促进了经济增长(付强和乔岳,2011[1]),以及促进了产业升级,这在东部地区尤为显著(崔志坤和李菁菁,2015[16])。中国的财政分权体制和晋升竞争体制使得地方政府具有强烈的动机干预企业投资和利用各种优惠政策招商引资,进而促进地区经济发展。钟笑寒(2005)[17]发现在规模经济递减的技术下,地区竞争加剧将提高社会福利,而在相反条件下,地区竞争更有可能降低了社会福利。相反地,有研究认为如果过于关注经济增长,地区竞争将降低教育支出占比(郑磊,2008[18]),加剧地方债务水平(邱栎桦和伏润民,2015[19])。
地区竞争加剧了对外资的竞争,并且对地区生产率产生显著影响。周黎安(2004)[5]研究表明财政分权改革的结果使得各地方政府具有相对独立的利益,加快了FDI的引进。Porter(1990)[20]认为竞争程度与产业生产率的关系呈倒“U”型,在曲线的前半段,竞争程度加剧可以促进企业创新,进而提高企业生产率,但竞争程度较高时,其对生产率提升作用出现停滞。我们认为,Porter的研究实际指出了可能存在门槛效应,Arrow(1962)[21]认为竞争程度过于激烈,可能减弱生产率的增长。相反地,李平等(2012)[22]研究发现在政府干预下的资本密集型行业的资源配置效率较低,加大开放和竞争程度更能提升工业部门的生产率。同时,我们认为中国地区经济发展水平高低不同,发展阶段也不同,对于外资影响生产率的门槛可能不同。
学者们的研究为本文提供了依据和论点支持,本文思路是在地区竞争机制存在的情况下,研究竞争行为对地方经济发展的影响,其中对外资的竞争是我们重点研究的对象。作为发展中国家,中国在经济发展初期是资本相当匮乏的国家,但是随着经济的发展,沿海发达地区可能率先完成初期的资本积累。那么,地区间对于外资竞争对生产率的提升作用将有所不同。哪些地区已经跨过了门槛?门槛值到底是多少?研究结论对地方政府的外资政策的设计和建议具有现实意义,而通过文献整理发现,这样的研究目前国内还较少涉及。2018年中美贸易摩擦给予我们很大启示,面对发展困境,国家领导人表示中国将以开放姿态面对国际经济和政治环境,主要是加大外资开放市场。那么,哪些地区更应该积极地接受外资,将其转化为经济发展过程中的资本积累?哪些地区不应该盲目地争夺外资或者更应该利用本地资本?我们的研究可以给出部分解释和建议。
三、理论模型、数据和变量说明
(一)理论模型
我们的研究结合经典理论,生产率(TFP)的变化体现了技术水平、资源优化和组织效率等变化,其背后的原因与引进外资、研发创新、引进国外先进生产工艺以及国家政策等因素有关。我们借鉴Conrad 和Wastl(1995)[23]、Greenstone等(2012)[24]的建模思路,使用CES函数形式建立生产函数,Y=AKαL1-α。其中Y为地区工业产出值,K为资本投入,L为劳动投入,并且0<α<1,A代表希克斯中性的生产率。为了模型简单化,我们将劳动投入单位简化为1。则y=Akα,y和k为人均产出和人均资本,在A不变的情况下,k越大则y越大。我们将公式进行变换,则TFP=yk-α,在y给定的情况下,k越大则TFP越大。我们进一步看k的边际影响,并区分为国内资本kd和外来资本kf,其中k=kd+kf,将y和TFP对kf求一阶导数和二阶导数,则相应的结果如公式(1)~公式(4)所示。
∂y/∂kf=Aaka-1>0
(1)
∂TFP/∂kf=-ayk-a-1<0
(2)
(∂y/∂kf)′=-Aa(1-a)ka-2<0
(3)
(∂TFP/∂kf)′=a(1+a)yk-a-2>0
(4)
从公式(1)和公式(2)可以看出,资本投入对产出的边际贡献是递增的,对生产率的边际贡献是递减的。并且,从公式(3)和公式(4)可以看出,二阶导数方向与一阶导数方向相反,说明资本投入的边际贡献的递增趋势和递减趋势都在变缓。即随着资本积累的增加,地区资本禀赋逐渐增大,则资本的边际(可以看作每年新增外资的变动)作用对地区的产出和生产率的作用在减弱,这与我们要研究的资本的门槛效应一致。我们认为,理论模型指出资本积累过程中,外来资本的边际作用在减弱,则可能存在门槛使得地方政府即使大力引进外资,但其促进作用相比资本积累初期将大大减弱。
(二)数据和变量说明
1.数据整理。
本文数据为2002—2011年省级层面数据,具体反映省份之间的差异,考虑到行业之间存在异质性,我们使用省级和行业层面数据[注]由于西藏、宁夏、贵州、青海、内蒙古5个省级地区数据缺失比较严重,本文对其进行剔除处理,最终包括有26个省级地区。。本文选取的各省份行业数据为规模以上工业企业统计口径,数据来源于《中国工业经济统计年鉴》(2003—2012)[注]本文数据来源于《中国工业经济统计年鉴》《中国能源统计年鉴》等,目前我们可以获得的《中国工业经济统计年鉴》截至2015年,《中国能源统计年鉴》截至2012年,考虑到数据可获得性,实际可以使用数据仅到2011年。更重要的是,2013年以后《中国工业经济统计年鉴》中不再统计工业总产值指标,因而不能准确测算地区行业层面的生产率。。数据整理时发现行业分类标准发生了变化,2005年以前有25个行业,2005年及以后有27个行业,后期相对前期新增了两个产业。为了保持前后数据的一致,我们采用2005年以前的行业分类标准。并且,有些产业数据缺失,我们将其删除,最终确定了18个产业(如表1所示),得到468个截面样本。

表1本文选择的行业描述
2.变量设定。
我们使用各省份分行业的生产率,具体用数据包络分析法(DEA-Malmquist)求出。由于计算出的数值都是环比数值,参照陈勇和李小平(2007)[25]的方法,本文将其折算到以2002年为基期的定比数值。对于外来资本竞争(RCP,下文简称资本竞争)现有文献有使用地区人均外资反映地方政府的竞争行为(张军等,2007[26]),韩超和王海(2014)[3]认为资本竞争是地方政府竞争的核心本质,外商投资相对国内资本更能反映地方政府的竞争程度。本文借鉴韩超和王海(2014)[3]变量构造方法,使用各省份相对人均外资作为资本竞争的代理变量,具体使用各地实际利用外商投资与全国实际利用外资额的比例表示。由于中国各地区的发展水平不同,地区竞争存在显著的地区差异,资本禀赋(CAEN)的差异是影响这一机制的重要因素,本文使用各省份人均资本形成额与全国人均资本形成额之差来表示。
为了排除其他因素的干扰,本文引入控制变量。产业结构(INST)用地区第二产业占GDP的比重来构建。城镇失业率(URA)用国家统计局公布的城镇失业率衡量。进出口程度(IEGDP)用各省份进出口额占GDP的比重衡量。所有制结构(OWNIP)使用各省份的国有及国有控股工业企业的资产合计值占规模以上工业企业资产合计值的比重来表示。地区发展水平(LNPGDP)使用各省级人均GDP的对数值构建,并使用GDP平减指数进行平减。市场开放程度(INDEX)使用樊纲等(2011)[27]公布的市场化指数表示,数据来源于《中国市场化指数》[注]2010和2011年没有出台市场化指数,如果剔除2010和2011年数据将会损失大量样本,加入解释变量主要是为了稳健性考虑,对文中的政策实验不会产生实质的影响,通过观察发现市场化指数一直处于稳步上升趋势,本文在2009年樊纲构造市场化指数基础上乘以前三年变化率的均值求出2010年市场化指数,2011年市场化指数使用类似方法求出。。控制变量数据来源于《中国工业经济统计年鉴》、各省统计年鉴和国家统计局,主要变量的描述性统计如表2所示。
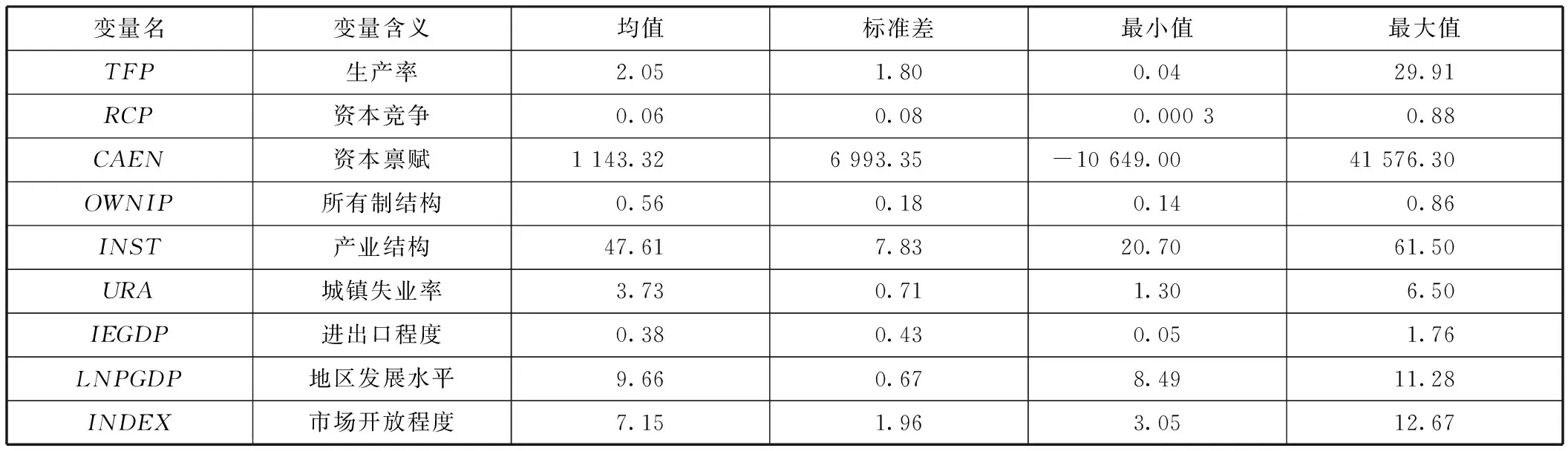
表2主要变量的描述性统计
四、全要素生产率的测算
对于全要素生产率(TFP)的测算,传统的方法是索罗剩余法,全要素生产率被理解为扣除要素贡献后的“剩余”生产率水平。索罗剩余法函数形式一般为柯布-道格拉斯(Cobb-Douglas)生产函数,但其面临着共时性问题(simultaneity bias)和样本选择(selection bias)问题,因此使用索罗剩余法计算的全要素生产率并不准确。对于上述情况,Olley和Pakes(1992)[28]提出的OP法以及Levinsohn和Petrin(2003)[29]在其基础上发展的LP法在本文均不具有可行性。OP法不仅可以解决共时性问题,且可以解决样本选择性偏误,但是OP法要求代理变量(投资)与总产出保持单调性,即要求投资始终为正值,但是本文在计算产业投资额时发现,计算的投资额并不是始终为正值,因此使用OP法不具有可行性。LP法不再使用投资作为代理变量,而是使用中间投入作为代理变量,但由于在产业层面,没有公开中间投入统计数据,同时在研究区间内,会计准则发生较大变化,因此使用LP法也不具有可行性。
本文使用数据包络分析法(DEA)计算全要素生产率,使用DEA方法的优势为:一方面是DEA方法不需要设定具体的函数形式,从而避免了由于主观因素造成的模型设定错误。另一方面是其他求效率的方法一般局限于单产出的情况下,而且需要将投入、产出变量折算为同一单位,相较之下,DEA方法不需要将投入、产出变量折算为同一单位,变量设置更为灵活。
(一)DEA的模型设定
DEA的最早模型是C2R模型,其假定企业生产的规模效益是不变的,只可以计算决策单元的综合技术效率。Banker等(1984)[30]在其基础上提出了BC2模型,假定生产的规模效益是可变的,计算出的生产率分解为纯技术效率和规模效率。中国是新兴经济体国家,相较西方等发达国家市场远未饱和,各行业的生产规模效益可变的特征显著,由此,本文适合采用BC2模型。假设模型中存在n个决策单元,其中每个单元有m种投入xi和s种产出yi,xij表示第i个单元的第j种投入变量,yir表示第i个单元的第r种产出变量。我们参照蒋萍和王勇(2011)[31]的方法,BC2模型可以表示为:
(5)
(6)
(7)
(8)
上述公式中,i=1,2,n;s-≥0,s+≥0;j=1,2,m;r=1,2,s。其中公式(5)是生产函数,公式(6)到公式(8)是相应的生产条件。公式(8)表示决策单元是规模效益可变的。θ为决策单元的有效值,s-和s+为松弛变量,ε为非阿基米德无穷小量。当θ=1,并且s-=s+=0时,表示决策单元为DEA有效;当θ=1且s+≠0或s-≠0时,则决策单元为DEA弱势有效;当θ<1时,决策单元不是DEA有效。Färe等(1992)[32]基于DEA模型构造了马奎斯特指数法(Malmquist),该种方法可以反映数据的动态变化。单纯使用DEA模型只能计算出行业年度静态全要素生产率,本文使用的是10年期的面板数据,只有结合马奎斯特指数(Malmquist)才能求出不同年份的全要素生产率。公式可以表示如下:
TPF=M(xt+1,yt+1;xt,yt)
(9)
(二)DEA-Malmquist阶段变量的设定
因为工业总产值、固定资产净值和投资都是当年价格,本文使用相应的平减指数进行折算。本文选取工业总产值作为产出变量,使用以不变基期的工业品出厂价格指数(PPI)进行折算,并用Y来表示。使用固定资产净值作为资本投入,以不变基期的固定资产投资价格指数(FPI)进行折算,并用K来表示。本文采用永续盘存法求得投资变量(鲁晓东和连玉君,2012[33]),公式可以表示为:It=(Kt-Kt-1)+(Dt-Dt-1)。其中Kt使用未平减前的固定资产净值表示,Dt为累积折旧额,使用不变基期的固定资产投资价格指数(FPI)进行折算,并用I来表示。使用从业人员年平均人数作为劳动投入变量,用L来表示。使用能源消耗总量作为能源投入变量,用E来表示,上述使用到的数据全部来源于《中国能源统计年鉴》。各投入变量和产出变量要满足“同向性”假设要求,即投入量增加时,产出量不应该减少,可以使用Spearman相关性检验。检验结果如表3所示,可以看出,投入、产出变量满足“同向性”假设要求。

表3投入变量与产出变量的Spearman相关系数
注:上述变量都是折算后的不变价格变量,相关系数均通过了5% 的显著性检验。
(三)回归结果
本文使用Deap2.1软件进行回归,为了体现出全要素生产率的年度变化情况,本文求出每年折算后的全要素生产率做算数平均,然后绘制出全要素生产率的年度变化图,如图1所示。从图1可以看出,全要素生产率总体上处于上升趋势,总体上和我国的经济发展形势相符。2008年全球经济危机爆发,年度平均全要素生产率出现轻微下降。原因在于2008年国际金融危机对中国出口贸易造成比较大的负面影响,继而造成全要素生产率下降。总体上看,计算的全要素生产率和现实情况相符,回归结果比较准确。
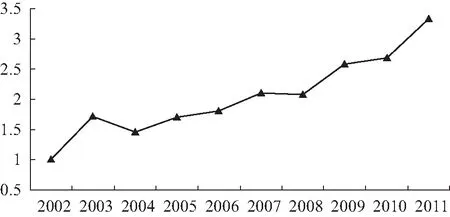
图1 定比生产率(TFP)年度变化趋势图
五、实证检验
(一)基本模型检验
本文通过Hausman检验,结果显示适合随机效应模型,在实证中我们使用混合OLS模型,并且逐渐加入控制变量来回归。具体如公式(10)所示,回归结果如表4所示。
TFPit=β1RCPit+β2CAENit+β3OWNIPit+β4INSTit
+β5URAit+β6IEGDP+β7LNPGDPit
+β8INDEXit+uit
(10)
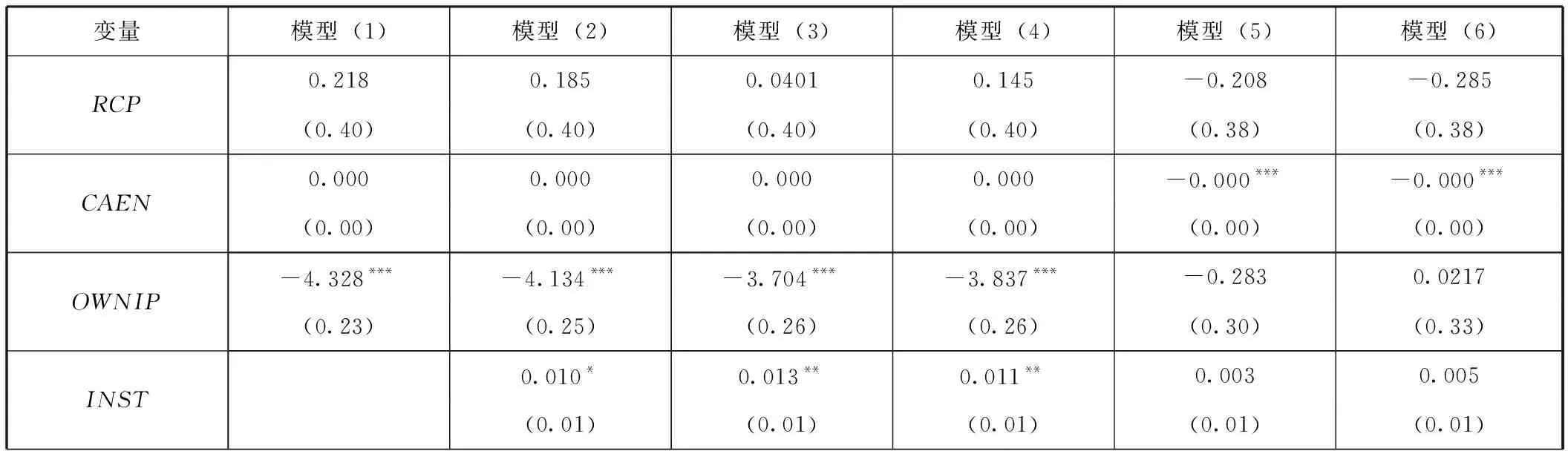
表4基本模型回归结果
续前表
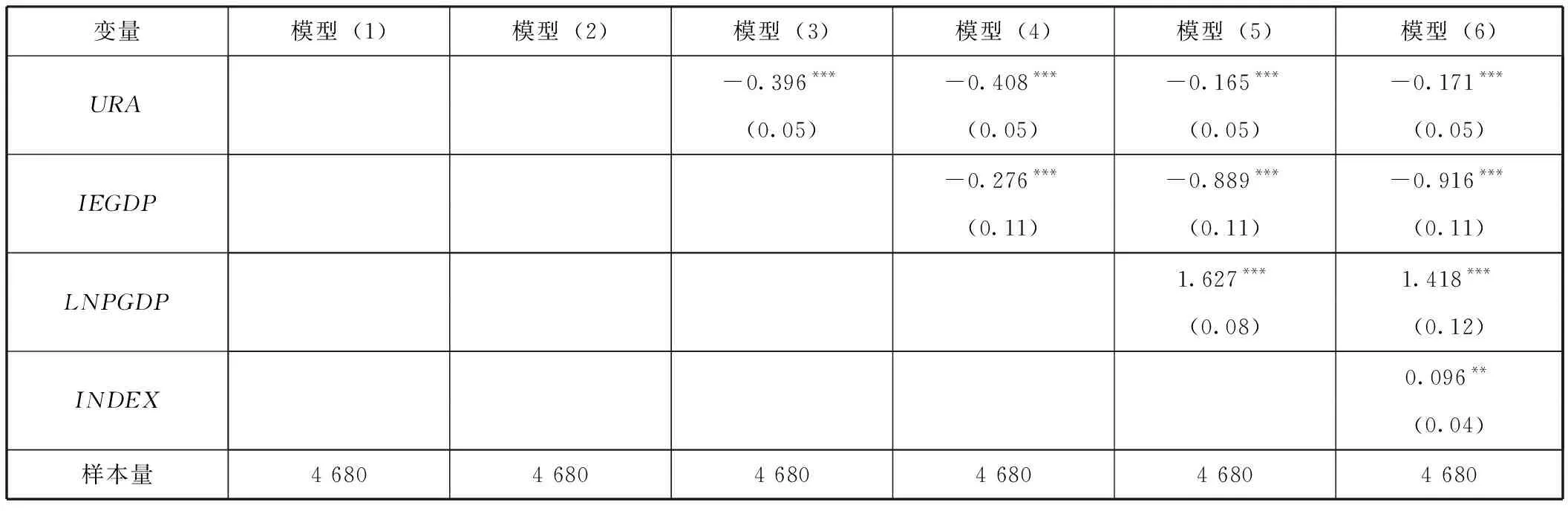
变量模型(1)模型(2)模型(3)模型(4)模型(5)模型(6)URA-0.396***-0.408***-0.165***-0.171***(0.05)(0.05)(0.05)(0.05)IEGDP-0.276***-0.889***-0.916***(0.11)(0.11)(0.11)LNPGDP1.627***1.418***(0.08)(0.12)INDEX0.096**(0.04)样本量4 6804 6804 6804 6804 6804 680

通过表4可以看出,随着控制变量的加入,资本竞争(RCP)系数符号逐步由正转负,回归结果表示资本竞争对生产效率具有负向效应,但是这一结果并不显著。资本禀赋(CAEN)变量符号逐步由正转负,在模型(5)和(6)中均通过了1%水平的显著性检验,表现出资本禀赋对全要素生产率的负向效应。对于其他控制变量,除所有制结构(OWNIP)在模型(6)中系数符号发生改变,其他变量系数符号都没有发生变化。
对于控制变量的解释。城镇失业率(URA)、进出口程度(IEGDP)、地区发展水平(LNPGDP)、市场开放程度(INDEX)在相应的模型中均通过了显著性检验,所有制结构(OWNIP)和产业结构(INST)仅在模型(5)和(6)中没有通过显著性检验。可以判断,国有资本比重过高并不利于全要素生产率的提升,对此国家应该继续推行国企改革,支持民营企业发展和引进外资。目前第二产业依旧是拉升我国企业全要素生产率的主要产业,我国第二产业占GDP的比重在50%左右,对此,在逐步增大第三产业比重并减小第二产业比重时,应该保留高效率的第二产业企业,但是模型(5)和(6)系数符号未变且没有通过显著性检验,对该变量有待进一步分析[注]由于第一产业在三大产业中比重较小,且变化不大,本文主要分析第二产业和第三产业的比重变化。。城镇失业率越高,地区全要素生产率越低,这和基本经济理论相符。进出口水平越高,则地区全要素生产率越低,原因在于我国出口产品还是以低端制造为主,从事的产业本身生产率较低。地区发展水平与全要素生产率呈正向关系,主要因为地区发展水平越高则产业竞争力越高。市场化水平越高,全要素生产率越高,说明扩大地区的市场开放程度有利于地区生产率的提升。
(二)资本禀赋门槛效应的识别
本文采用Hansen面板数据门槛模型进行实证检验(Gregory和Hansen,1996[6];Hansen,1999[34]),选取资本禀赋(CAEN)作为门槛变量,由于模型中如果遗漏变量,模型估计结果将不准确(Hansen,2000[35]),本文将全部引入控制变量来减小模型设定偏误,构造的面板门槛方程如式(11)所示。
TFPit=Ci+∑(Xijtγi)+θ1RCPit
×d(CAENit<τ1)+θ2RCPit
×d(τ1 ×d(τn-1 (11) 其中:CAENit表示资本禀赋;RCPit表示资本竞争,d(·)表示门槛函数;Xijt表示一个包含OWNIPit、INSTit、URAit、IEGDPit、LNPGDPit、INDEXit、CAENit等变量的矩阵;γi为列向量;εit表示随机扰动项,并且假设其服从均值为零且方差有限的正态分布。由于本文使用的是面板数据,有必要对门槛变量CAEN进行平稳性检验。本文采用了LLC检验,检验P值为0.00,检验结果拒绝原假设,即门槛变量CAEN通过单位根检验,门槛变量体现出平稳性,符合作为门槛变量的基本条件。 根据Hansen(2000)[35]面板数据门槛模型的设定,主要分三个步骤进行检验:一是对参数进行估计,求出门槛值τ并估计斜率的系数;二是门槛效应是否通过显著检验;三是检验门槛值,构建门槛值τ的置信区间。在确定一个门槛效应的基础上,检验是否存在第二个门槛效应,依次类推。对于门槛值τ的估计需要将资本禀赋(CAEN)的每一个观测值代入回归模型,并进行基于OLS的回归。本文具体以资本禀赋(CAEN)为门槛变量,用自举的方法计算出F值和P值,最终得出面板数据门槛的估计值和门槛效应检验结果,如表5所示。可以发现,文中单一门槛模型、双门槛模型和三门槛模型均通过了显著性检验,可见模型具有显著的三门槛效应,故本文选取三门槛模型进行分析。 表5资本禀赋的门槛数量识别检验 注:软件设置为自助抽样选择300次。 图2 资本禀赋门槛值 从门槛识别检验可知,资本禀赋在本文中是一个重要的门槛变量。资本竞争对全要素生产率的影响与资本禀赋存在必然联系。本文以资本禀赋作为门槛变量,使用三门槛模型对这一影响进行估计,如公式(12)所示,门槛模型回归结果如表6所示。从表6的可知,对于控制变量,除了进出口程度(IEGDP)和市场开放程度(INDEX)没有通过显著性检验外,其他变量均通过了显著性检验。 TFPit=Ci+γ1OWNIPit+γ2INSTit+γ3URAit +γ4IEGDPit+γ5LNPGDPit+γ6INDEXit +γ7CAENit+θ1RCPit×d(CAENit <-8 507.46)+θ2RCPit×d(-8 507.46 ≤CAENit<-5 304.22)+θ3RCPit ×d(-5 304.22≤CAENit<4 033.18) +θ4RCPit×d(CAENit≥4 033.18)+εit (12) 表6门槛效应实证结果 对于核心变量的解释,资本禀赋(CAEN)系数符号由负转正且通过了显著性检验,说明资本禀赋程度越高越有利于地区生产率的提升。资本竞争(RCP)对产业生产率的影响存在显著的三门槛效应。从回归结果看,资本竞争(RCP)通过了显著性检验且系数符号为正,说明地区资本竞争对产业生产率的提升具有促进作用。但是资本竞争对产业生产率的提升作用在不同资本禀赋程度下的影响程度有显著不同。当地区人均资本低于全国平均资本8 507.46元/人时,资本竞争对地区生产率的促进作用最大。当资本禀赋逐渐增加,与全国的人均水平相差不是很大时,即差距在(-8 507.46,-5 304.22)时,资本竞争对地区生产率的促进作用减小。当资本禀赋逐渐增加,同时与全国的人均水平差距在(-5 304.22,4 033.18)时,地区竞争对产业竞争力的促进作用进一步缩小。当地区人均资本高于全国平均资本4 033.18元/人,地区竞争对产业竞争力的促进作用变得不显著且回归系数进一步缩小。 本文将10年来各省级地区的资本禀赋求均值,发现没有省份资本禀赋均值小于-8 507.46[注]只有甘肃、安徽和江西个别年份出现资本禀赋小于-8 507.46,样本数量为4个,不具有代表性,本文将不做讨论。,处于(-8 507.46,-5 304.22)的地区是甘肃,资本禀赋均值大于4 033.18的地区有6个,包括辽宁、浙江、江苏、北京、天津和上海,其他地区资本禀赋均值处于(-5 304.22,4 033.18)。说明辽宁、浙江、江苏、北京、天津和上海的地区资本竞争不会对产业生产率产生正向效应,沿海省份资本相对充裕,大多完成了初期的资本积累。这6个省份应注重利用本地现有资本,地方政府应把精力放在本地资本消化上以及引进高质量FDI,而不是盲目地招商引资。其他地区的资本竞争对地区生产率的效应没有达到最大,应当大力引进外资投入本地资本积累。 对于控制变量的解释。相较于混合面板OLS回归结果,所有制结构(OWNIP)、城镇失业率(URA)和地区发展水平(LNPGDP)的系数符号没有发生改变,经济学含义与前文相同。进出口程度(INDEX)的系数符号发生了改变,但是没有通过显著性检验。市场开放程度(INDEX)没有通过显著性检验,系数符号没有改变。产业结构(INST)的系数符号由正转负,且通过了显著性检验,第三产业的全要素生产率一般高于第二产业,这也是第二产业比重逐步缩小,第三产业比重逐步扩大的原因。本文认为在当今产业结构转型时期,应当大力发展第三产业,提升第三产业占GDP的比重,同时继续发展第二产业中生产率较高的行业。 综合来看,本文认为资本禀赋和地区竞争对产业竞争力的提升都会产生促进作用,但是资本禀赋的门槛效应也是存在的。可以看出,资本禀赋程度越低,地区竞争对产业竞争力的提升作用越强。一方面,地区资本禀赋越富足,代表地区内资本满足自身需求的程度越高,进而引进外来资本的动力越小,使用外商投资衡量的地区竞争程度就越低,地区竞争对地区生产率的正向促进作用越低。另一方面,中国劳动力、资源环境等相对优势使得规模经济特征显著,在全球生产格局中,产业层次较低并且以劳动密集型产业居多。外国资本也乐意投资于见效快、生产效率低的产业,比如简单加工装配行业,这部分资本大多流向发展中国家。 此外,使用人均资本衡量的资本禀赋,代表了国内资本和外来资本的沉淀,也间接体现了外资投向低端产业的程度。我们认为,资本禀赋越高,外资流向低端产业的程度越高,则产业生产率反而越低。对此,地方政府应当引进优质和高质量资本,引导外来资本投向资本密集型和技术密集型等发展潜力和竞争力高的产业。 1994年后的分税制改革和以GDP为导向的官员晋升机制使得地方政府有更多的权利激励干预经济政策。进而地区间竞争加剧,地区竞争势必对地区经济发展产生影响,从微观层面上对地区生产率产生影响。本文主要研究了地区资本竞争对生产率的影响。通过面板数据三门槛模型实证检验得出:中国地区间的资本竞争对产业生产率具有促进作用,但是存在资本禀赋的三门槛效应。地区资本禀赋越低,地区竞争对产业竞争力的正向影响效应越大;当资本禀赋丰富到一定程度后,这种正向影响效应将不显著。本文认为地区资本禀赋较高时,地区对外商投资需求较小,进而减弱了地区的资本竞争程度,其对产业生产率的影响减小。同时,外商投资进入资本密集型和技术密集型的比例相对较小,并且更容易流向产生效益快和低效率的产业,从而对地区生产率的提升作用有限。我们认为,地方政府应当引导外资更多地投向发展潜力大和生产率高的行业。 完善改革外商投资(FDI)引入政策,积极推进优质资本与项目引入。资本竞争是当期FDI衡量的地区竞争程度, FDI通过沉淀为本地资本进而成为资本禀赋的一部分。从前文实证部分可知,随着资本禀赋的增高,资本竞争对地区生产率的正向效应逐渐减弱。我们认为中国劳动力、资源等比较优势决定了产业布局集中于劳动密集型等国际分工体系处于较低位置的产业,有些低效率的产业反而能够快速获得利润,比如劳动密集型的出口加工行业。对于能带来效率提升的优质资本,比如在国际产业价值链中处于较高位置以及技术和资本密集型的产业,发达国家较少向发展中国家输出,这也是中国开放外资市场并且呼吁美国等西方国家放松高端技术和高质量资本管制的矛盾所在。通过资本竞争机制引进的FDI,最终沉淀为本地资本禀赋的一部分,如果这些资本仅仅流向低效率的产业(企业),并不会对本地产业竞争力带来多大的提升作用。本文认为地方政府在引进FDI时应该有意识地引进技术含量高、资源消耗低的优质资本,对于流向低效率产业的资本给予限额,对流向高效率产业的资本给予政策扶持。 适时调整产业政策,积极推进优质资本与项目引入,更加注重资本与项目的质量。资本禀赋的三门槛效应显著存在,在不同的地区资本禀赋的情况下,资本竞争对产业全要素生产的正向影响效应存在差异,并且随着地区资本禀赋程度的提高,正向影响作用逐渐减弱。本文认为地区资本禀赋包括了本地资本和外来资本。当地区资本禀赋足够高时,则地区资本禀赋可以满足本地需求,地方政府对FDI引进动力就会减弱,进而使用FDI衡量的地区竞争程度就会降低,资本竞争对产业生产率的促进作用就会减弱。如果地区拥有较高的资源禀赋,地方政府用于引进FDI而付出的努力并不会有效提升产业竞争力,反而可能造成资源的浪费和资本在地区间的错配。本文认为,地方政府的招商引资政策不应该盲目跟风,应该结合本地区的资本禀赋情况,制定符合本地的招商引资政策和计划。 深入推进国有企业向混合所有制改革,激发国有资产活力。无论是从面板数据混合OLS模型还是门槛模型的回归结果来看,所有制结构对地区生产率都有显著的负向作用。可见,地区国有资产比重越高,则产业生产率越低。国有资本效率低下已经成为制约产业竞争力提升的重要因素,政府应当进一步激活国有资本活力,加快推进混合所有制改革进而提高地区生产效率和竞争力。

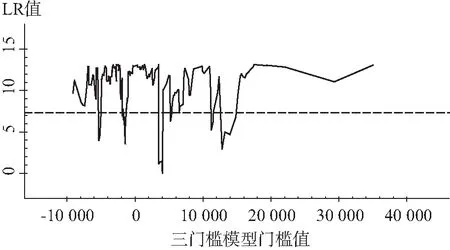
(三)资本门槛效应下资本竞争对产业生产率的影响

六、结论与政策建议
(一)结论
(二)政策建议

