基于响应面法PLA的3D打印工艺参数优化＊

刘月云，盛信仁，张 静

江苏食品药品职业技术学院（江苏淮安 223005）

1 引言

随着3D打印技术的迅速发展，小型桌面级3D打印机因具有结构灵活多样、操作简单、占用面积小等优点而被越来越普遍地应用。在使用桌面3D打印机打印过程中，打印工艺参数对产品的尺寸精度和表面粗糙度有着重要的影响。在所有打印工艺参数中，打印层高、打印温度及打印速度是较为关键的3个工艺参数[1]。PLA和ABS两种线材是桌面3D打印机打印中常用的材料，其中PLA材料作为新型的生物基及可再生生物降解材料，环保性显著优于其它材料，迅速得到广泛应用[2]。本文将3D打印件的表面粗糙度为质量目标，通过响应面法来优化PLA的打印层高、打印温度和打印速度3个工艺参数，为PLA线材的3D打印工艺参数选取提供经验参考。

2 试验材料及设备

2.1 试验材料

聚乳酸（PLA）：线材直径φ1.75mm，密度为1.250.05g/cm3，打印温度200℃～230℃。

2.2 试验设备

FDM桌面级3D打印机：H1D-1MM-00024型双喷头3D打印机，额定电压为220V、50HZ，额定功率350W，3D打印机如图1所示。

图1 桌面级3D打印机

表面粗糙度仪：徕斯达TR200型高精度表面粗糙度仪，测量范围为Ra0.05～12.0μm。

3 响应面试验

3.1 试验方案与结果

响应面法是利用合理的试验设计采用多项式函数来拟合试验因素与响应值之间的函数关系，并通过对回归方程的分析来寻求最佳工艺参数，是解决多变量问题的一种统计方法[3]。

响应面试验中的BBD设计是一种独立的二次方设计，它不包含嵌入式因子或者分级因子，在BBD设计里试验点是立方体各个棱上的中点的组合，所有的试验因素具有旋转性，用于试验因素较少的情况，每个因素一般需要3个水平[4]。在本试验的BBD设计中，选取打印层高度（A）、喷头温度（B）及打印速度（C）作为试验因素，以3D打印件的表面粗糙度为响应值，具体的BBD试验因素、水平及编码如表1所示。

BBD试验规划方案与经过3D打印试验所得的表面粗糙度值如表2所示。

3.2 方差分析及响应面模型建立

运用Design-Expert软件对表2中的试验数据进行方差分析，得到的3D打印件表面粗糙度与打印工艺参数之间响应面模型的方差分析结果如表3所示。

从表3可以看出响应面模型的F值为165.26，意味着模型在统计学上是有意义的，仅有0.01%的概率会产生噪音。“P值”小于0.05时候，代表此项显著，即对响应面模型的影响大，从表3中的“P值”可以发现对3D打印件表面粗糙度影响较大的项有A-A、B-B、C-C、A2、B2、C2。A-A及A2的“P值”都小于0.0001，这表明，在3个打印工艺参数中，打印层高对3D打印件表面粗糙度的影响最为显著。

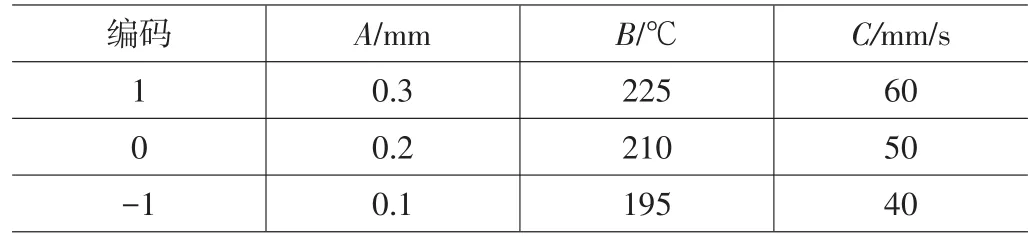
表1 BBD试验因素、水平及编码

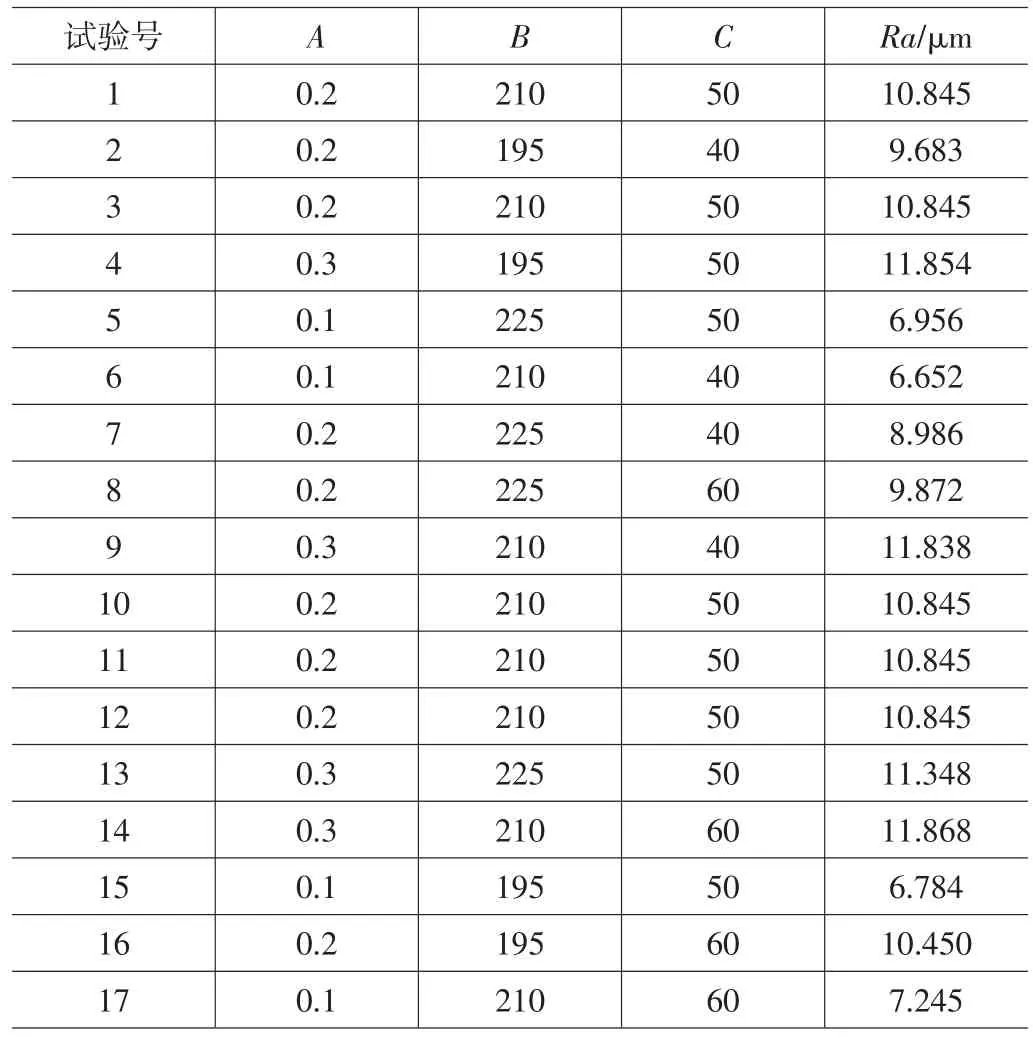
表2 BBD试验方案与结果

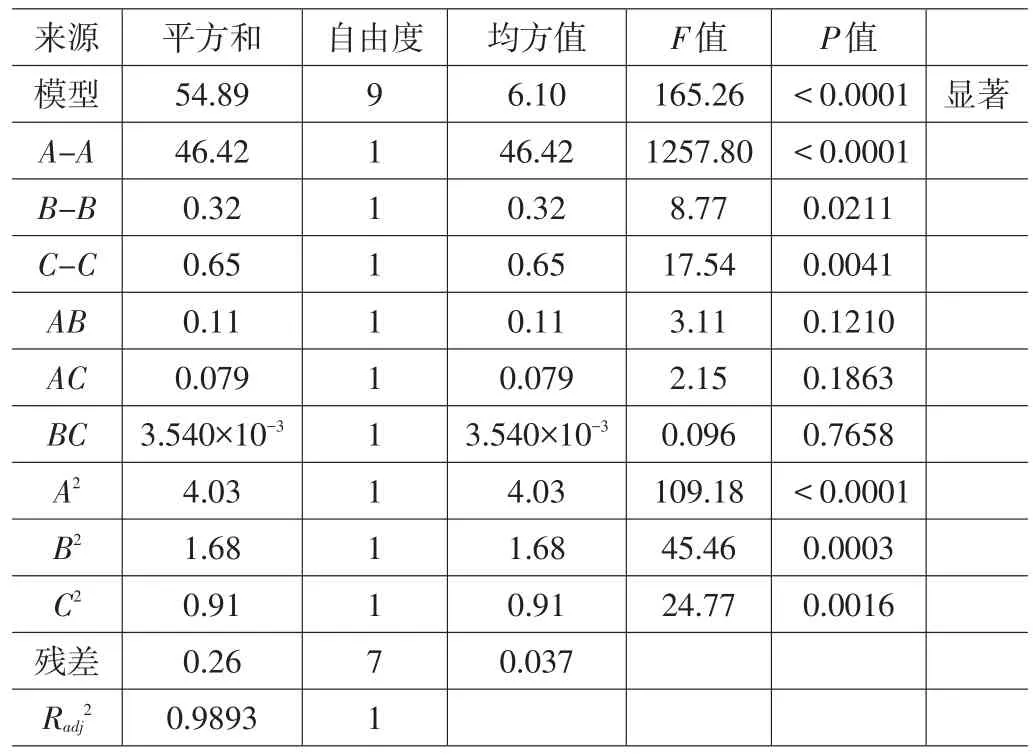
表3 响应面模型的方差分析结果

响应面模型是通过构造响应面模型近似表达式代替设计问题中隐式的约束或目标函数，即利用多项式函数通过最小二乘法拟合设计空间[5]。PLA的3D打印件表面粗糙度与打印工艺参数之间的关系形式未知，可用二阶响应面模型来构建二者之间函数关系，其数学表达式为：

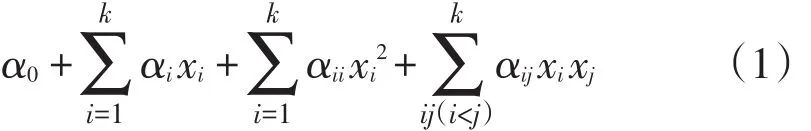
式中 y（x）——响应值，即表面粗糙度值

x——试验变量，即3D打印工艺参数

α——各项系数

k——待优化工艺参数的数量

结合公式（1）的函数关系式及表2的试验结果，运用Design-Expert软件对二阶多项式

回归拟合分析，获得3D打印件表面粗糙度与打印工艺参数之间的二阶响应面模型为：

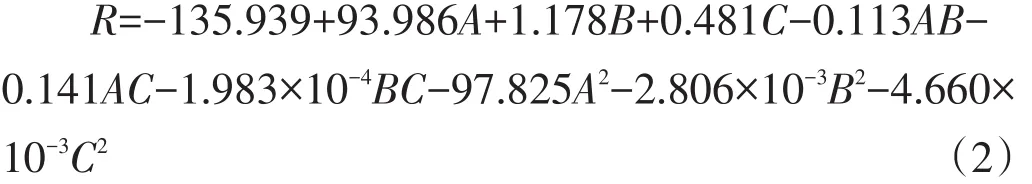
式中 R——表面粗糙度值，μm

A——3D打印出层高，mm

B——喷头温度，℃

C——打印速度，mm/s

3.3 响应面模型检验

经过Design-Expert软件分析得到所构建响应面模型的残差正态概率情况如图2所示。由图2可见响应面模型的残差序列点呈正态分布于一条直线附近，这说明模型残差满足最小二乘拟合要求。

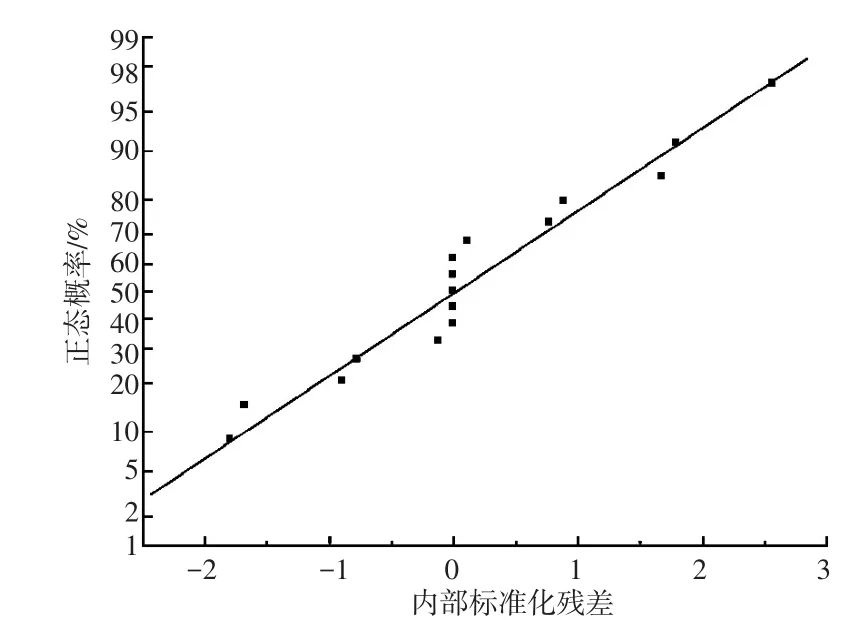
图2 残差正态概率图

另外，响应面模型的修正系数Radj2越接近于1，则模型的拟合精度越高，从表3可知该响应面模型的修正系数Radj2为0.9893，说明响应面模型的拟合精度高。

4 响应面模型优化及试验验证

4.1 响应面模型优化

以3D打印件的表面粗糙度的最小值为目标，根据构建的响应面模型对3D打印工艺参数进行优化，得到的最小表面粗糙度值为5.874μm，对应的打印工艺参数为：3D打印层高度为0.12mm；喷头温度为224.50℃；打印速度为40.39mm/s。

4.2 试验验证

利用优化出的3D打印工艺参数进行PLA的3D打印试验，得出的打印件表面粗糙度为6.125μm，与响应面模型优化值相比，误差为4.1%，误差较小，响应面优化效果好。

5 结论

（1）选取影响3D打印件表面粗糙度的打印层高度、喷头温度及打印速度等3个工艺参数为试验因素，以表面粗糙度为响应值进行响应面试验，建立它们之间的精度较高的二阶响应面模型，方差分析得出打印层高对打印件表面粗糙度的影响最为显著。

（2）运用建立好的二阶响应面模型进行优化分析，优化出3D打印件表面粗糙度最小值为5.874μm。而使用优化后的3D打印工艺参数进行PLA打印试验所得的打印件表面粗糙度值为6.125μm，二者误差仅为4.1%，优化效果较好。