液态排渣煤粉燃烧器燃烧温度影响因素分析
贾明生,张林锋,扶廷正,陈 赛
(1.广东海洋大学机械与动力工程学院,广东湛江524088;2.浙江富春江环保科技研究有限公司,浙江杭州311401)
燃烧温度是反映燃烧热状态的重要参数之一,对于液态排渣煤粉燃烧器而言,其不仅影响飞灰含碳量的高低[1]、液态捕渣量的多少及煤粉燃烧过程中NOx的生成量[2-6],还直接关系到燃烧器能否持续稳定运行。液态排渣煤粉燃烧器属于旋风燃烧方式,其特点介于层燃和室燃之间,兼有并突出了这两种方式的长处。对于液态排渣煤粉燃烧器,燃烧室内的燃烧温度过低,筒壁熔渣膜难以达到软化和熔融状态,导致液渣量偏小、排渣不顺畅;燃烧温度过高,燃烧室炉衬表面渣膜变薄,热阻减小,传热量增大,难以实现“以渣抗渣”,燃烧室炉衬易被高温烟气侵蚀烧坏[7]。因此,在实际运行过程中,合理调控液态排渣煤粉燃烧器内的燃烧温度非常重要。影响燃烧器内的燃烧温度因素众多,本文仅研究热风温度、过量空气系数、冷却水带走热量比例、热负荷、煤低位发热量等五个因素对燃烧温度的影响规律和影响程度。
1 燃烧温度的计算
1.1 燃烧热平衡模型的建立
液态排渣煤粉燃烧器在运行过程中通常温度高达1 600℃以上,燃烧室需采用水冷膜式壁,水冷壁外表面附着一层耐火材料,内置金属销钉。燃烧室采用冷却水进行冷却才能在高温条件下持久稳定地工作,冷却水带走热量作为燃烧器输出热量的一部分。建立燃烧热平衡模型时,需作如下假定:①煤灰中不含固定碳,煤粉的机械不完全燃烧热损失不计;②煤粉和二次风中的水分会与煤粉分解后的焦炭发生水煤气反应,吸收部分热量,但该反应发生的程度较低,不作考虑;③灰分中的SiO2会与煤粉分解后的焦炭发生还原反应,SiO2气化成SiO,消耗部分热量[8],该反应发生比较困难,不作考虑;④燃烧产物中CO2和H2O会存在高温离解的情况,其分解程度与体系的温度及压力有关,在压强为0.1×105~5×105Pa,温度低于2 100℃时,燃烧产物热分解现象及其影响较小[9],忽略不计这部分热量;⑤由于燃烧反应产物中H2和CmHn等含量极低,化学不完全燃烧热损失仅考虑CO的不完全燃烧热损失。基于上述假定条件,煤粉完全燃烧时,热平衡模型的各输入热量项、输出热量项如图1所示。
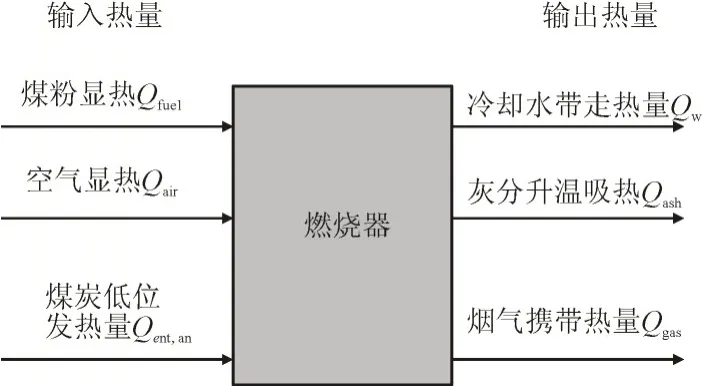
图1 燃料完全燃烧时燃烧器热平衡模型
当过量空气系数小于1,燃料不完全燃烧时,热平衡模型中总输入热量需减去CO的不完全燃烧热损失。由热平衡模型可得燃烧温度的计算公式如式(1)所示。
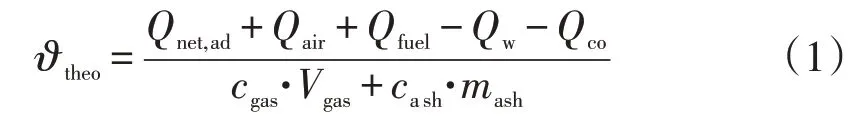
式中:ϑtheo为燃烧温度,℃;Qnet,ad为燃料空气干燥基低位发热量,kJ/kg;Qair为空气带入的物理热,kJ/kg;Qfuel为燃料带入的物理热,kJ/kg;Qw为冷却水带走热量,kJ/kg;Qco为CO不完全燃烧热损失,kJ/kg;cgas为气体燃烧产物的平均比热容,kJ/(m3·℃)(标准);Vgas为气体燃烧产物生成量,m3/kg(标准);cash为燃烧产物中灰分的平均热容,kJ/(kg·℃);mash为燃烧产物中灰分的质量,kg。
1.2 过量空气时的燃烧温度计算
煤粉在过量空气情况下完全燃烧时,可以认为不存在CO不完全燃烧热损失项。因此,燃烧器总输入热量由煤低位发热量Qnet,ad、空气带入热量Qair及燃料带入热量Qfuel三部分组成,总输出热量由烟气携带热量Qgas、灰分升温耗热Qash及冷却水带走热量Qw三部分组成。计算用煤种的燃料特性如表1所示。

表1 燃料特性
现以文献[10]中高效低NOx煤粉工业锅炉所搭载液态排渣煤粉燃烧器作为计算对象,选取过量空气系数α为1.2,大气温度为30℃,一次风温度为50℃,一次风占总风量比例为10%,二次热风温度为250℃,1 kg煤粉带入物理热Qfuel为16.371 kJ,冷却水带走热量占总输入热量的10%。在文献[11]中考虑灰分的理论燃烧温度计算模型基础上,将冷却水带走热量纳入输出热量的一部分,按上述方法经计算得到燃烧温度为ϑ=1 719.76℃。
1.3 欠氧燃烧时的燃烧温度计算
文献[11]中给出了燃料完全时建立的燃烧温度方程,但没有给出欠氧燃烧条件下燃烧温度方程的建立。鉴于此,本文基于方程求解法建立欠氧燃烧时燃烧温度的计算模型。为了得到不同煤种下的燃烧温度方程,将煤粉中各成分设置为变量如表2所示,其中变量x1~x7满足x1+x2+x3+x4+x5+x6+x7=100。

表2 煤粉成分的变量设置
根据燃烧化学反应方程式及碳元素和氧元素守恒可计算得到由x1~x6表示的烟气各成分含量Vi0,设Vi0=b1x1+b2x2+b3x3+b4x4+b5x5+b6x6(其中i=N2、H2O、RO2、CO,下同),则欠氧燃烧时烟气各成分含量由x1~x6表示的各系数如表3所示。
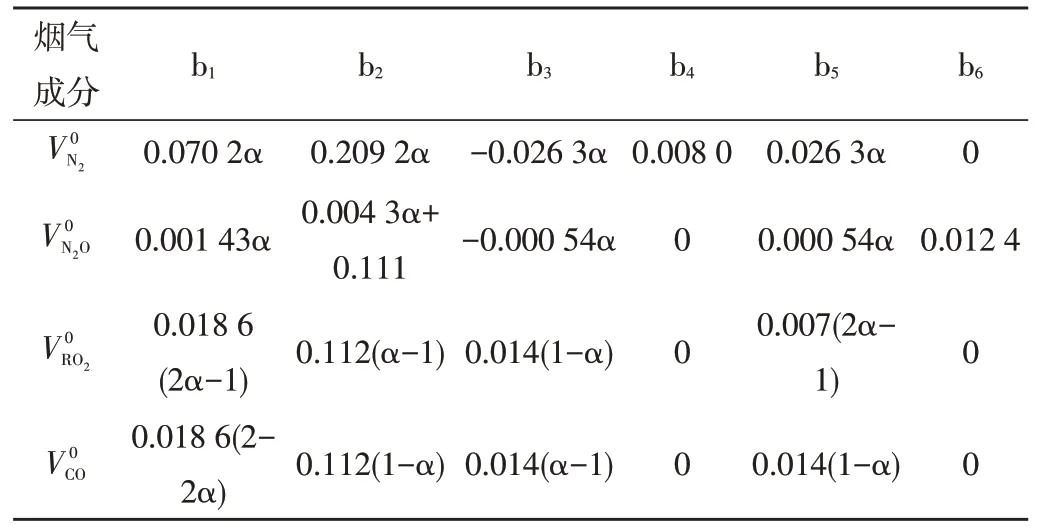
表3 欠氧燃烧时理论烟气各成分含量系数
设Q2由烟气携带热量Qgas和灰分携带热量Qash两部分组成,则Q2可由下式求得:
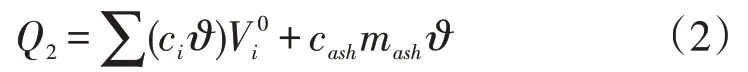
根据表3、式(2)及文献[11]中各烟气成分平均比热的拟合结果,可计算得到欠氧燃烧时Q2关于变量x1~x7及过量空气系数α和温度ϑ的矩阵表达式如下:
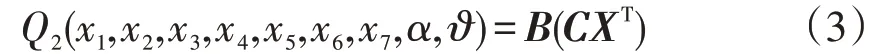
其中矩阵C、B、X如下:

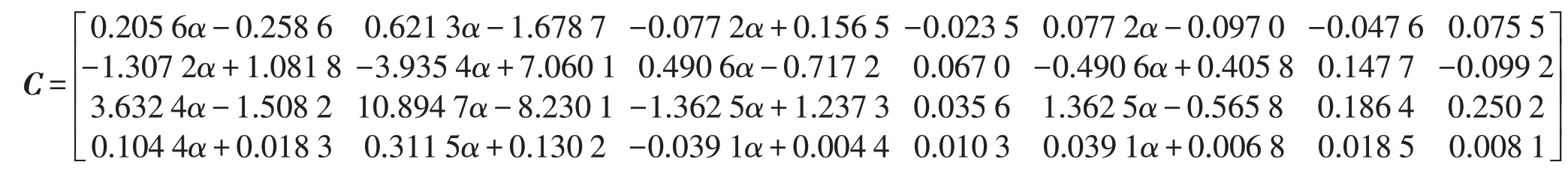
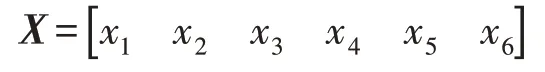
欠氧燃烧较之过量空气燃烧,总输入热量需减去CO的不完全燃烧热损失Qco,计算公式如下式(4):

由总输入热量等于总输出热量,可得:
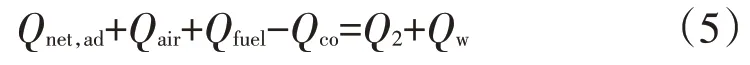
式(5)即为欠氧燃烧时的燃烧温度方程,其中Q2由式(3)确定,当过量空气系数α为0.8,其他计算条件不变时,可计算得到ϑ=1 722.28℃。
2 燃烧温度影响因素分析
以文献[10]中的高效低NOx煤粉燃烧器作为计算对象,选择燃料特性如表1所示,按上述燃烧温度的计算方法,研究热风温度、过量空气系数、冷却水带走热量比例、热负荷、煤低位发热量等五个因素对燃烧温度的影响规律。
2.1 热风温度对燃烧温度的影响
二次热风是空气与锅炉尾部烟气换热得到的,热风温度不超过350℃。冷却水泵转速是根据冷却水温度进行变频调节的,根据长期运行情况,以文献[10]中燃烧器的冷却水带走热量基本维持在2 149.6 kJ/kg左右,取过量空气系数α为1.2。经计算得到热风温度在100~350℃变化时,燃烧器的燃烧温度变化情况如图2所示。
二次热风作为燃烧器输入热量来源之一,燃烧温度与热风温度必定呈正相关。从图2可以看到,燃烧温度与热风温度呈强线性关系,且热风温度每升高1℃,燃烧温度约提高0.56℃。
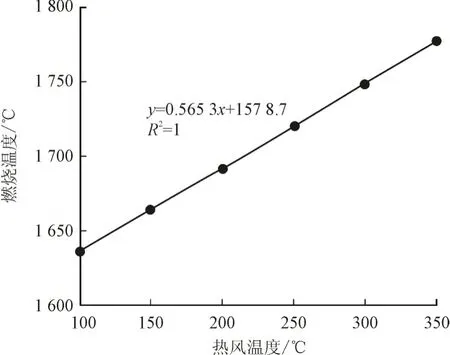
图2 热风温度对燃烧温度的影响趋势
2.2 过量空气系数α对燃烧温度的影响
设热风温度为250℃,计算得到过量空气系数α在0.7~1.4变化时,燃烧器的燃烧温度变化情况如图3所示。
从图3可以看到,过量空气系数α对燃烧温度有显著影响。当α<1时,燃烧温度随着过量空气系数的增大而升高,说明因燃烬率提高释放的热量要比因空气量增多而吸收的热量多;当α>1时,燃烧温度随着过量空气系数的增大而降低,此时空气量增多吸收更多的热量是燃烧温度降低的主导因素。可见过量空气系数α过高或过低均不利于维持一个合适的燃烧温度范围,在燃烧器运行时,需要对鼓风机、引风机进行适当调节,使过量空气系数α稳定在某最佳值附近。

图3 过量空气系数对燃烧温度的影响
2.3 冷却水带走热量对燃烧温度的影响
设热风温度为250℃,过量空气系数为1.2,计算得到冷却水带走不同比例热量情况下,燃烧器燃烧温度的变化趋势如图4所示。
从图4可以看出,冷却水带走热量占煤粉有效输入热量之比从0%增至12%,燃烧温度相应地从1 891.9℃下降至1 685.3℃,燃烧温度与冷却水带走热量比例呈现强负线性相关,且冷却水带走热量比例每增加一个百分点,燃烧温度下降17.2℃。
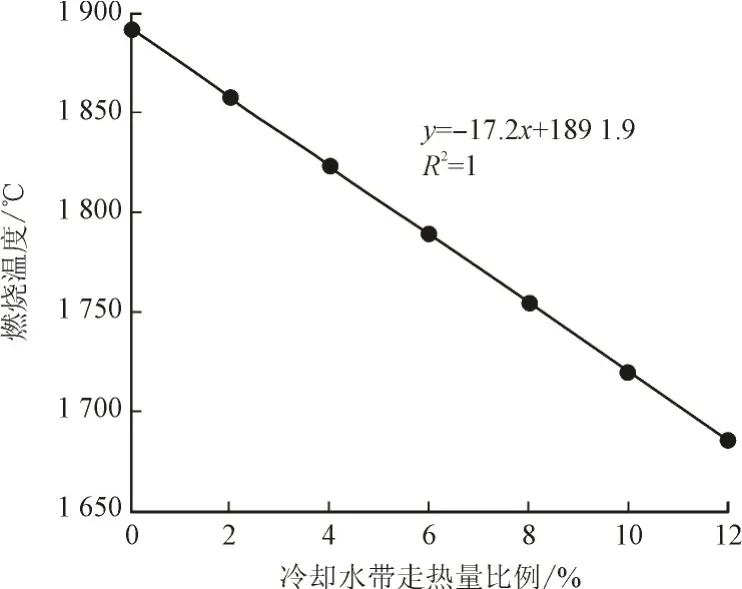
图4 冷却水带走热量比例对燃烧温度的影响
2.4 热负荷对燃烧温度的影响
设热风温度为250℃,在过量空气系数α分别为1.1和1.2时,通过计算得到不同热负荷下燃烧温度的变化情况如图5所示。

图5 热负荷对燃烧温度的影响
从图5可以看到,每增加1%热负荷,燃烧温度上升2.8℃左右,热负荷对燃烧温度的影响并不大,原因在于热负荷增加一倍的同时,在保持过量空气系数不变的情况下,烟气量也增加了一倍。另外,热负荷对燃烧温度施加的影响受过量空气系数影响不大,每增加1%热负荷,α为1.2时燃烧温度上升2.7℃,α为1.1时燃烧温度上升2.9℃,变化幅度比较接近。
2.5 煤低位发热量对燃烧温度的影响
煤粉低位发热量作为最主要的输入热量来源,其大小势必影响燃烧温度。以1 kg煤粉作为计算度量,设热风温度为250℃,过量空气系数为1.2时,计算得到51种不同煤种的燃烧温度,燃烧温度随煤低位发热量的变化情况如图6所示。从整体来看,燃烧温度随着煤低位发热量的增大而呈现升高趋势,但并不是随着低位发热量的增大而严格的升高,即使某相近低位发热量的两煤种,燃烧温度也可能相差较大,这与王世昌[12]对158种动力煤绝热燃烧温度的研究结果具有一致性。实际上煤低位发热量是由煤成分参数决定的,而煤成分不同又导致理论空气量不同,由于煤成分不同对二者的影响并不总是同步的,因此燃烧温度随煤低位发热量的变化并不是严格递增的。
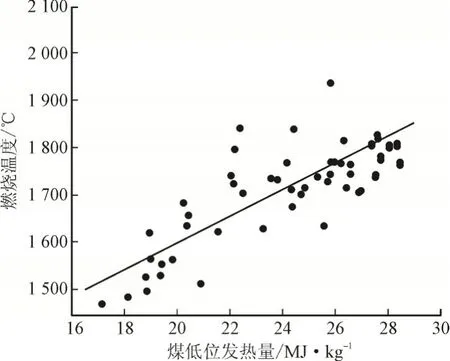
图6 燃烧温度随煤低位发热量变化情况
3 燃烧温度影响因素的灰色关联分析
为了确定燃烧温度的各影响因素对其影响程度,明确哪些是主要因素,哪些是次要因素,采取灰色关联分析的方法进行研究分析[13-14]。它是从系统离乱的、随机的行为特征量中确定因素间关联程度的一种分析方法,是基于行为因子序列的微观或宏观几何接近程度,对样本容量和数据有无规律情况没有要求。
设有m个比较序列Xi和s个参考序列Yj,记为

则比较序列Xi中某元素xi(k)和参考序列Yj中元素yj(k)的关联系数ξji(k)可由下式计算:
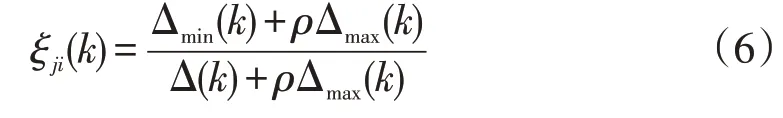
式中:Δ(k)=|yj(k)-xi(k)|,Δmax(k)和Δmin(k)分别表示参考序列元素与对应比较序列元素绝对差值中的最大值和最小值,ρ为分辨系数,通常取ρ=0.5。
关联系数是比较数列与参考数列在各个时刻的关联程度值,为了从总体上了解序列之间的关联程度,求其平均值,作为比较数列与参考数列间关联程度的数量表示,即灰色关联度rji,可由下式计算:

按灰色关联度分析原则,关联度越大的比较序列与参考序列越为接近,即是影响参考序列指标越主要的因素。因此,按照计算出的关联度值便可排列出比较序列对参考序列影响程度的大小次序。
当煤种一定时,可调节的变量为热风温度(X1)、过量空气系数(X2)、冷却水带走热量比例(X3)及负荷(X4),以这4个因素序列为比较序列,以燃烧温度(Y)为参考序列,对表4中20组数据进行均值化处理,使各序列无量纲化并处于同一数量级后,进行灰色关联分析。
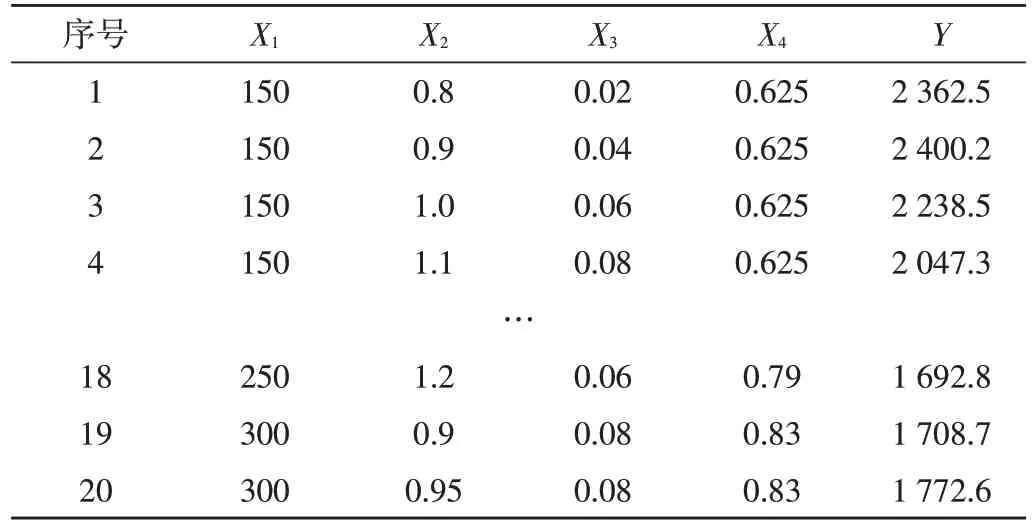
表4 燃烧温度与各影响因素一览表
经计算,得到灰色关联度序列为r={0.688 6,0.690 9,0.569 8,0.616 5},各影响因素对燃烧温度的关联度顺序为:X2>X1>X4>X3。因此,当煤种一定时,其他几个因素对燃烧器燃烧温度的影响程度依次为:过量空气系数>热风温度>负荷>冷却水带走热量比例。
4 结论
本研究针对液态排渣煤粉燃烧器基于方程求解法建立了燃烧温度计算模型,可简捷、准确地求解燃烧温度[11]。在此基础上,研究分析了燃烧器燃烧温度影响因素。通过各影响因素与燃烧温度的灰色关联分析,明确了各影响因素对燃烧器燃烧温度的影响程度。得出如下结论:
(1)热风温度、负荷与燃烧温度呈强正线性相关关系;冷却水带走热量比例与燃烧温度呈强负线性相关关系;过量空气系数与燃烧温度呈非线性关系,过量空气系数为1时,燃烧温度达到最大值,过量空气系数偏离1到两侧时,燃烧温度均呈下降趋势;燃煤低位发热量与燃烧温度具有较强正相关关系。
(2)煤种一定时,热风温度、过量空气系数、冷却水带走热量比例及负荷对燃烧温度的影响程度从高到低依次为:过量空气系数>热风温度>负荷>冷却水带走热量比例。

