不同降雨条件下裂隙性土质边坡渗流特性分析

万思豪 张继勋 张景风

(河海大学 水利水电学院，南京 210098)

0 引 言

降雨是自然界普遍的现象，其对边坡稳定产生不利影响，降雨入渗的过程中，水分渗入坡体内部，地下水位升高，孔隙水压力的增加导致坡体下滑力增大，降雨入渗过程中土体抗剪强度等物理力学性质会随着饱和度的增加而变化，降低了土体的抗剪强度[1-2].同时，土质边坡具有胀缩性及裂隙性[3-4]，裂隙的存在破坏了土体的完整性，显著改变了降雨入渗条件下的渗流分布.目前已有许多学者对降雨条件下的含裂隙边坡进行了研究：如姚海林等[5]研究了降雨强度对膨胀含裂隙边坡的影响；郑少河等[6]对裂隙性膨胀土饱和-非饱和降雨入渗过程进行分析；刘华强[7]对考虑降雨情况下的裂隙性膨胀土进行了边坡渗流稳定的分析方法研究.总体来说，目前研究成果多集中在仅考虑单一降雨条件下的裂隙性土质边坡稳定，研究降雨强度及降雨类型对裂隙性土质边坡渗流特性影响的并不多见，结合气象部门的降雨标准模拟降雨强度的更是少之又少，相应的规律还有待总结.

本文基于饱和-非饱和渗流理论，结合国家气象部门的降雨标准，选取小雨、中雨及大雨3种降雨强度，对前锋型、平均型、中锋型及后锋型4种不同降雨类型，运用Geo-studio有限元分析软件中的Seep/w模块研究了不同降雨强度、不同降雨类型下考虑裂隙深度、裂隙孔隙比的裂隙边坡渗流特性，以期得到相关规律，为对应工况下的滑坡稳定提供参考.

1 计算理论

边坡降雨入渗过程中边坡土体经历了一个非饱和-饱和渗流过程.土质边坡或存在裂隙发育边坡的降雨入渗问题均可采用等效连续介质模型进行分析，其控制方程为：

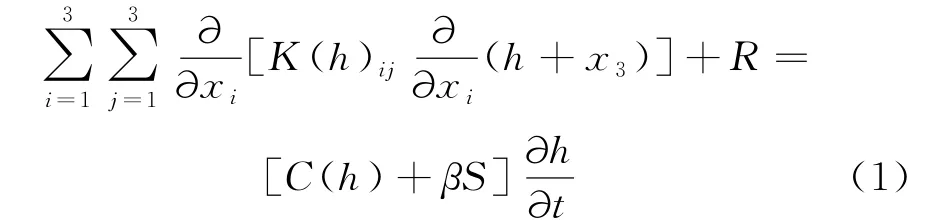
式中，h为饱和区压力水头，在非饱和区为基质吸力的势函数，简称基质势；C(h)为比水容量，表示单位土体压力水头降低一个单位所释放出的水体体积；K(h)ij为渗透系数，处于非饱和区时为基质势h的函数；S为贮水系数；β在非饱和区取1，饱和区取为0；R为源项.

用数值方法研究裂隙边坡，对裂隙的模拟主要有两类，一种是认为裂隙在雨水入渗时很快饱和，将裂隙作为水头处理，另一种是将裂隙等效为不同于原状土的均质材料.前种方法较为复杂且计算量大，一般很少采用.本文采用第二种方法，认为裂隙边坡由裂隙土及原状土构成.对于原状土及裂隙土的土水特征和渗透系数，引用Van Genuchten[8]提出的闭合方程进行拟合估算.

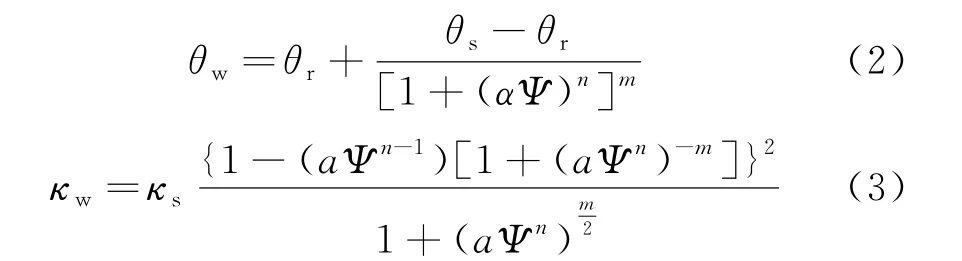
式中，θw为含水率；θs为饱和含水率；θr为残余含水率；κs为饱和渗透系数；κw为不同基质吸力下土体的渗透系数；Ψ为土体的基质吸力；α，m，n均为闭合方程的拟合参数，.

对于裂隙本身诱导产生各向异性的相关理论，根据袁俊平[9]、殷宗泽等[10]的相关研究，不同的裂隙深度、裂隙方向与垂直裂隙方向渗透系数的比值ε(简称渗透比)都会对降雨入渗的渗流场分布产生较大影响.因此，在研究不同降雨强度、不同雨型条件下裂隙边坡渗流特性时，有必要将裂隙的开展深度、裂隙孔隙比也考虑在内.

2 计算模型、参数与计算方案

2.1 模型建立

模型参照浙江省宁波市镇海区某土质边坡，地下水位距离不透水层约3m，坡顶长5m，坡高4m，坡比为1∶2，坡底长5m，裂隙设置于坡顶x=5处，沿裂隙面从上至下每隔0.5m 设一监测如图1所示.模型上表面均为降雨入渗边界，模型网格全局剖分810个单元，860个节点，如图2所示.

初始渗流场取为如图1所示的初始地下水位下的渗流场，其边界条件为：x轴为不透水边界；地下水位线以下左右边界为零流量边界、水位线以上左右边界为不透水边界；边坡表面为降雨入渗边界，当降雨强度大于土体的渗透系数时，入渗强度为土体的渗透系数数值大小，反之则为降雨强度的数值大小.

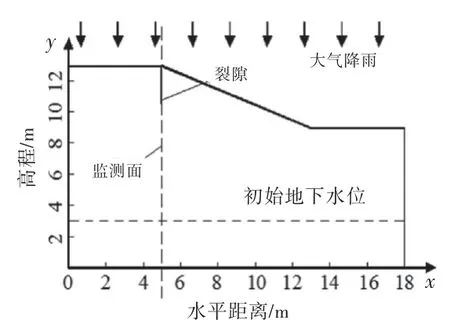
图1 计算模型

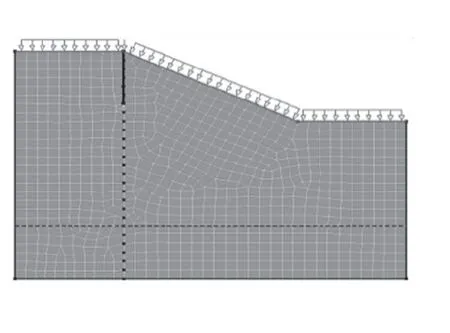
图2 有限元网格图

2.2 计算参数及计算方案

原状土参数参考文献[9]：α=166.7kPa，n=1.567，θs=0.495cm3/cm3，θr=0.262cm3/cm3，ksat=2.83×10-2cm/d.裂隙土参数在原状土基础上考虑饱和渗透系数不同，裂隙土垂直裂隙方向的饱和渗透系数ksatx=2.83cm/d.用VG 模型进行拟合估算得到渗透系数及土水特征.

根据国家气象部门规定的降雨量标准，降雨可分为小雨(0～10mm/d)、中雨(10～25mm/d)、大雨(25～50mm/d)、暴雨(50～100mm/d)、大暴雨(100～250mm/d)和特大暴雨(＞250mm/d)共6种各类雨的降水量，本文研究前3种常遇的降雨强度，即小雨、中雨和大雨，分别取10mm/d、24mm/d 和48 mm/d进行计算.再分别结合平均型、前锋型、中锋型及后锋型4种不同降雨类型，总计12种降雨情况，考虑降雨时长为24h，停雨12h，降雨过程如图3所示.

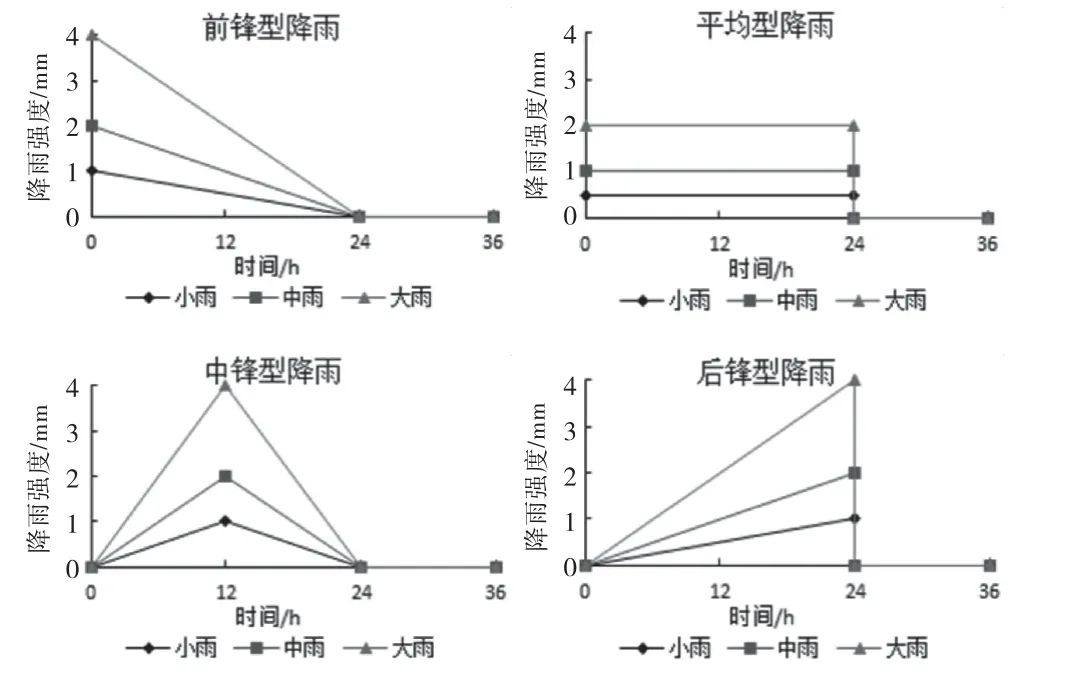
图3 降雨过程图

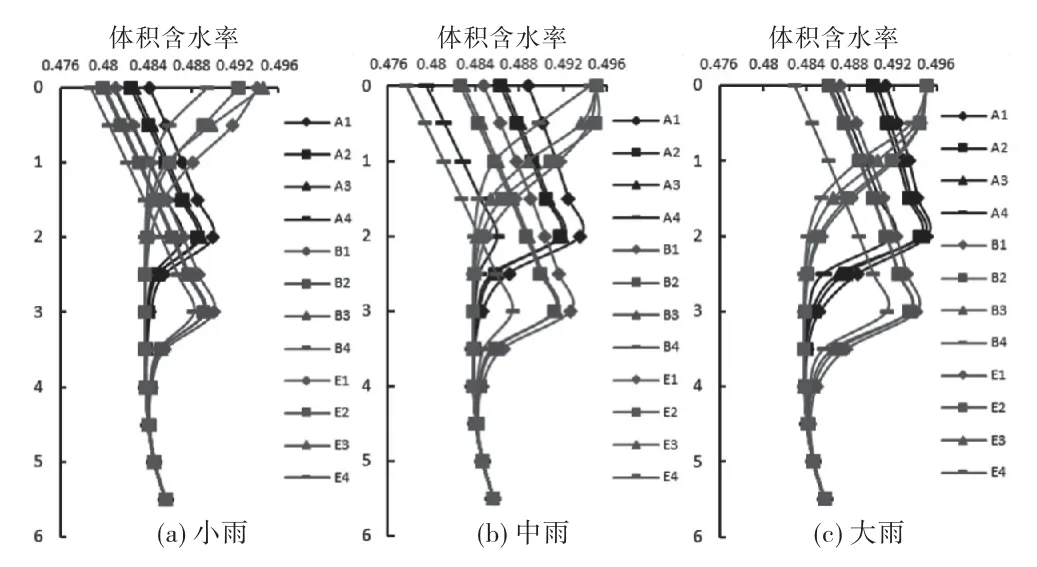
图4 工况A、B、E情况下降雨历时12h体积含水率变化图

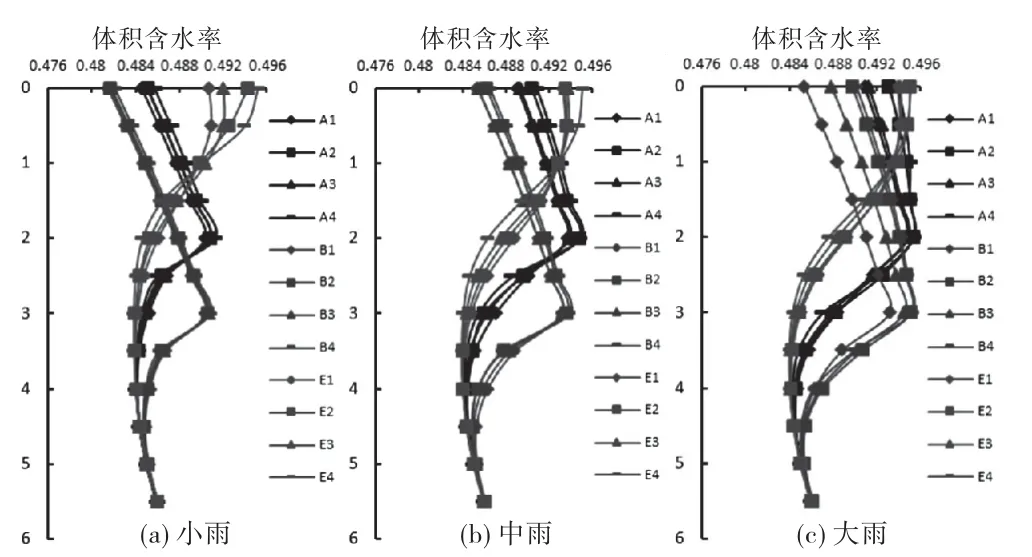
图5 工况A、B、E情况下降雨历时24h体积含水率变化图

考虑到裂隙深度对降雨入渗的影响，方案A、B取不同裂隙深度进行模拟计算，裂隙开展深度根据相关经验分别取2m、3m.同时，考虑裂隙渗透比对降雨入渗的影响，方案C、D、B分别取ε为1、10、100.方案E为不含裂隙的原状均质土坡在不同类型降雨条件下的工况.具体计算方案见表1.

表1 计算方案

3 计算结果及分析

3.1 裂隙深度不同情况下考虑雨强及雨型的渗流特性

裂隙深度为2 m 及裂隙深度为3 m 情况下，体积含水率随深度(m)变化情况如图4～6所示.

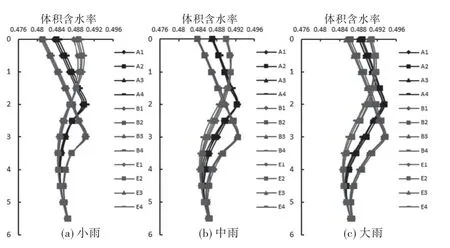
图6 工况A、B、E情况下降雨历时36h体积含水率变化图

由图4～6的(a)可见，对于无裂隙的原状土，雨水入渗土体由表及里，土体表层最先达到饱和，湿润锋向下发展，体积含水率随深度增大逐渐递减.对于考虑不同裂隙深度的含裂隙边坡，体积含水率随深度变化呈现出一个反S型.这是由于裂隙边坡因裂隙的存在，雨水下渗速率变大，水分难聚集，裂隙区域土体较难达到饱和状态，故裂隙土体区域体积含水率随深度增加而增大，裂隙埋深之下则恢复随深度增加而减小的趋势，由于存在地下水位，体积含水率减小到一定“转承值”时，又会随深度逐渐增大，直至地下水位处.因此，含裂隙土体的体积含水率沿埋深变化呈反S型.同时，不同裂隙深度决定反S型的拐点位置，裂隙深度越大，表层土体体积含水率越小，裂隙区域达到饱和状态所需时间越长.

不同降雨类型由于降雨的不均匀性，使得不同时段体积含水率在数值上呈现不同规律.对于无裂隙原状土，在降雨初期，前锋型降雨表层土体体积含水率迅速增大，在降雨后期，后锋型降雨土体体积含水率最大.这种降雨不均所带来的差异性在停雨后增加逐渐缩小，至停雨12h后，不同类型降雨的影响几乎为零.不同雨强情况下，降雨强度越大，降雨前期的土体体积含水率增长越快，到达饱和所需时间越短.当强度增大到一定值时，由于土体饱和或接近饱和，雨强影响减小，例如图5中平均型降雨，由小雨到中雨，表层土体体积含水率明显增大，而由中雨到大雨，表层土体体积含水率几乎不变.对于含裂隙土体而言，不同雨型及雨强对其渗流过程的影响大体与无裂隙原状土一致.

对于土体的孔隙水压力，各降雨类型孔隙水变化趋势与体积含水率变化相似，下面给出大雨情况下孔隙水压力随埋深(m)的变化，如图7所示.可以发现，含裂隙工况下，孔压变化明显不同于无裂隙土工况，裂隙土体内部孔压变化规律同样呈反S型.不同降雨类型对孔压的影响仍是由降雨分布不均造成，且在降雨后12h影响几乎消失.不同裂隙深度决定了反S型的拐点深度.

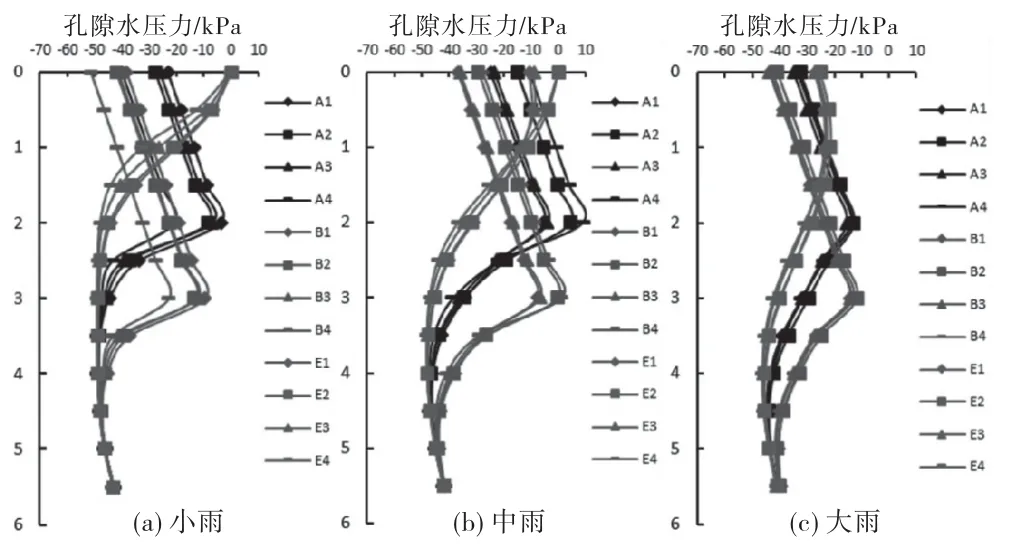
图7 大雨情况下工况A、B、E孔隙水压力变化图

3.2 裂隙孔隙渗透比不同情况下考虑雨强及雨型的渗流特性

裂隙孔隙渗透比为1和10情况下，土体体积含水率随深度(m)变化情况如图8～10所示.

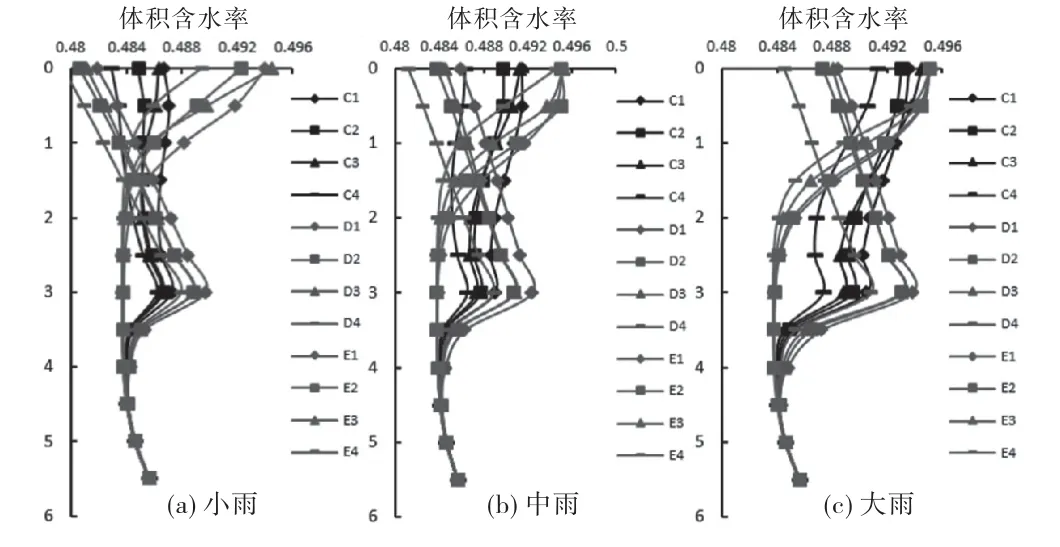
图8 工况C、D、E情况下降雨历时12h体积含水率变化图

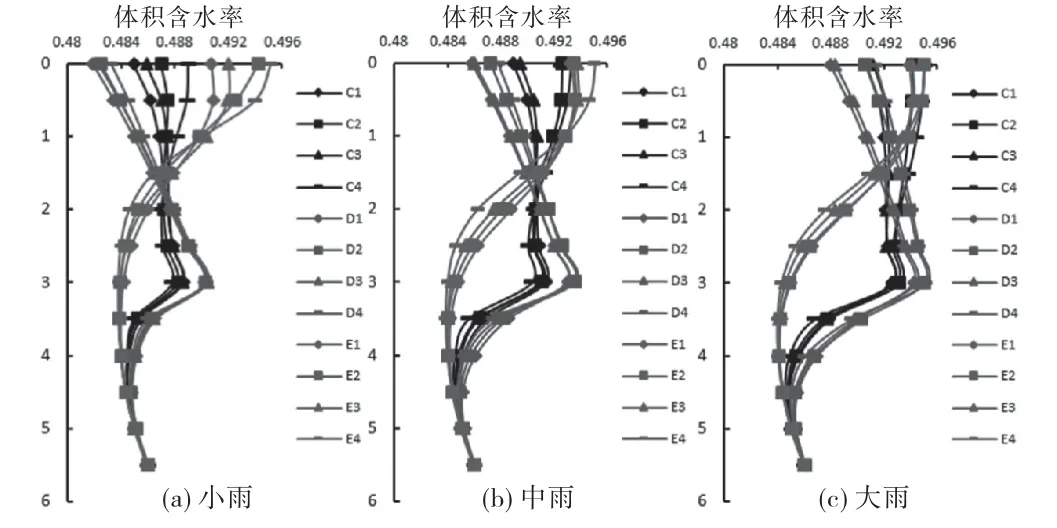
图9 工况C、D、E情况下降雨历时24h体积含水率变化图

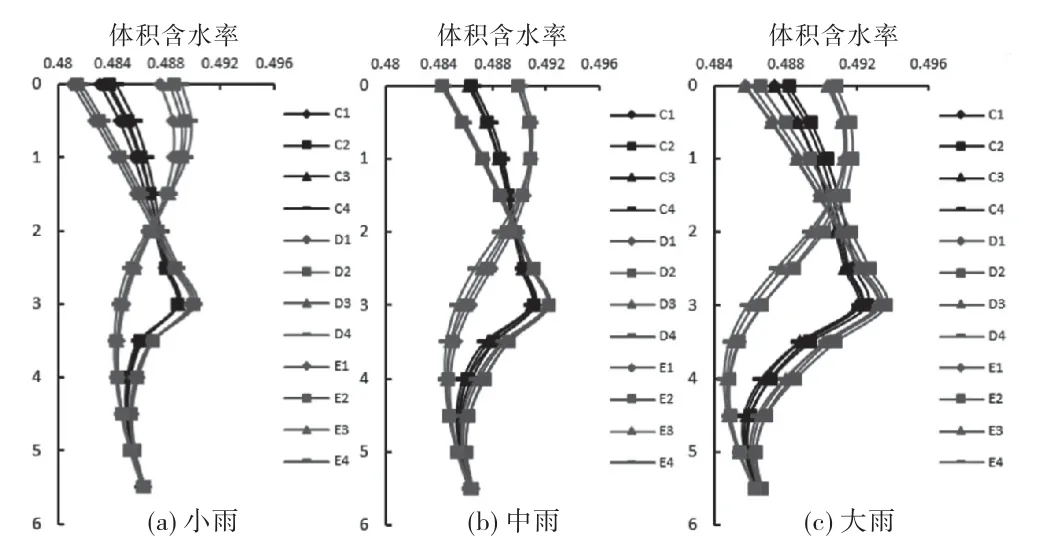
图10 工况C、D、E情况下降雨历时36h体积含水率变化图

不含裂隙原状土边坡在不同降雨条件下土体体积含水率随深度增大而减小.对于考虑不同渗透比的含裂隙土坡，由图6～8可见：ε=1的体积含水率随埋深增大而减小直至“转承点”，这是由于渗透系数较小，雨水无法快速下渗，从而在浅层土体积含水量较大，使土体含水量会随着深度增大而呈现逐渐减小的趋势；ε=10的体积含水率随埋深呈反S型，是因为裂隙土渗透系数较大，雨水在裂隙中快速下渗.

不同降雨强度对不同裂隙孔隙比的边坡土体体积含水量变化影响较大.以图9中ε=1的平均型降雨为例，在小雨情况下，平均型降雨浅层土体出现一小段范围沿埋深增大体积含水量也增大，而在中雨情况下这一范围进一步缩小，在大雨情况下已经消失了.这是因为当降雨强度较小时，表层入渗雨量还未超过土体的下渗能力，在表层某一范围内下渗快，从而出现浅层土体小范围随深度增大而增大.随着降雨强度变大，这一范围也随之消失.可以推测，当降雨强度足够大时，不同ε值裂隙边坡土体体积含水量随埋深变化趋势相同，均随埋深增加而增加.同时，将工况D 与工况B 进行比较，发现ε=10和ε=100的情况下，变化规律几乎相同，可以推测，对应于某一降雨强度，存在一临界ε'，当ε大于ε'时，裂隙渗透比再增大时，影响差异并不明显.

对于孔隙水压力，同样给出大雨情况下孔隙水压力随埋深(m)的变化，如图11所示.可以看到，大雨情况下同一降雨类型下，裂隙渗透比ε为1及10的孔隙水压力呈现不同规律.ε=1时，孔隙水压力随深度增大而减小，绝对值增大，主要是因为体积含水率随深度增大而减小，而当裂隙体积含水率减小时，不饱和度增大所造成.ε=10时，孔隙水压力随深度增大而减小.不同降雨类型带来的影响主要还是由于降雨分布不均所造成，且在停雨12h后影响几乎消失.

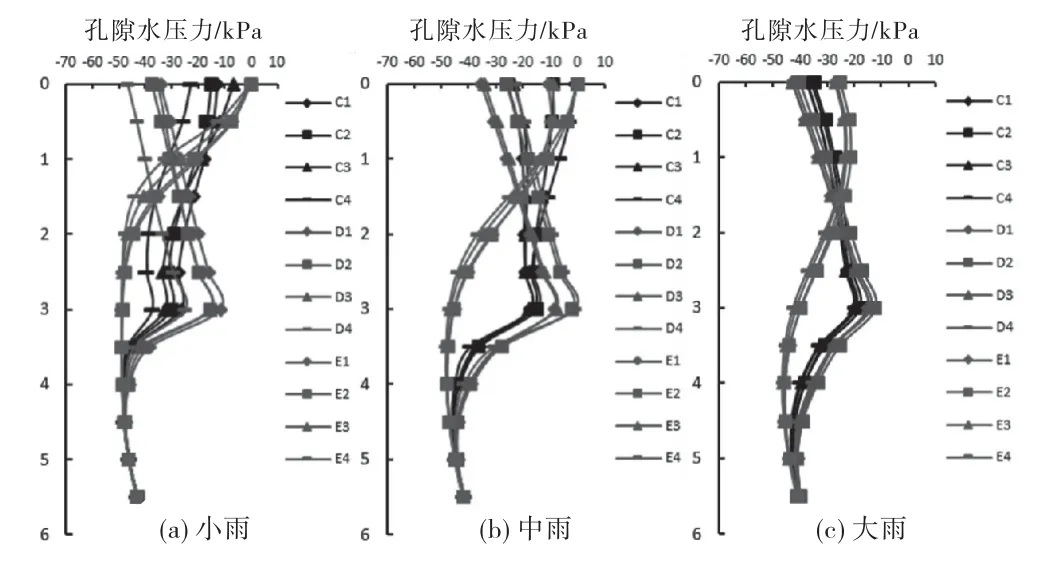
图11 大雨情况下工况C、D、E孔隙水压力变化图

4 结 论

1)裂隙渗透比越大，雨水下渗越快，对应相应降雨强度存在一“临介渗透比ε'”，当渗透比大于ε'，体积含水率及孔压表现出一致规律，即在裂隙区域随埋深增大而增大.当小于ε'时，随埋深增大而减小.

2)裂隙性土质边坡在ε大于ε'时，不同雨强及雨型条件下土体体积含水率及孔压随埋深变化均呈反S型，即先随埋深增大逐渐增大，到达拐点后随埋深增大而减小，最后再一次随埋深增大而增大.拐点深度取决于裂隙深度.

3)不同降雨类型由于降雨的不均匀性，影响裂隙边坡土体在某一时段内土体体积含水量及孔压数值上的差异.但对于整体趋势影响不大，并且不同降雨类型带来的影响在停雨后一段时间即会消失.

4)不同降雨强度对含裂隙边坡影响较大，降雨强度越大，含裂隙边坡土体达到饱和时间越短，但当降雨强度增大到一定值时，降雨强度大于土体入渗强度，降雨入渗将由土体渗透系数控制.对于不同裂隙孔隙比，当降雨强度足够大时，不同孔隙比下的裂隙土体体积含水率变化趋势将会相同，均随埋深增加而增加.