一种基于外罚函数法的结构可靠性分析方法

王林军 王 锬 杜义贤 徐 柳 黄文超 刘晋玮

(三峡大学 机械与动力学院，湖北 宜昌 443002)

在产品设计及可靠性分析中 ，一定使用条件下及寿命周期内能否完成预定功能是可靠性的评估依据.可靠性是产品的质量指标，贯穿于产品的设计、制造、开发、使用、试验、维修保养等各个环节.同时为了保证结构的安全性、适用性和经济性，在设计时也需要采用合适的方法加以分析和制约[1].目前已经有比较成熟及完善的可靠性分析方法，如一次二阶矩(FORM)[2]、二次二阶矩(SORM)[3]、基于可靠性分析优化设计(RBDO)[4]等，上述方法中例如一次二阶矩(FORM)方法计算简易，若所计算的精度要求不太高时，仍具有一定的实用价值.但是对于非线性程度较高的功能函数，就会有一定的非线性函数线性化带来的误差.国内外学者针对以上问题做了大量的研究.范松等[5]提出了一种基于证据理论的结构可靠性优化设计方法，从外层约束和内层约束两方面出发，使用约束可靠性的近似梯度来进行可靠性分析，解决了内层证据可靠性分析的效率问题；刘杰等[6]将泛灰数引入到结构模糊可靠度计算中，得出了较为精确的结构可靠度计算结果；Ashok Bakkiyaraj等[7]提出一种评估复合电力系统可靠性指标的新方法，该系统采用二进制差分法金华算法(BDE)在搜索机制中选择系统状态，对分析较少数量的系统状态的可靠性评估具有一定的作用，但是BDE 不适用于优化非线性目标函数的传统应用；姜潮等[8]提出了一种高效的概率-证据混合可靠性分析方法，通过引入概率-证据混合模型，建立可靠性优化设计方法，成功解决了混合可靠性分析中计算量过大的问题；马德仲[9]提出了基于贝叶斯网络和多源信息构建的可靠性分析模型方法，该方法适用于表达和分析不确定性事物，因而在可靠性分析领域得到推广应用；郑静等[10]提出了一种随机-认知不确定性的相关性分析模型及可靠性计算方法，马冬娟等[11]提出基于区间分析的非概率可靠性分析方法，该方法解决了一些实际问题中存在变量不确定性的情形，具有重要的理论意义.

实际上，上述方法虽然在一定程度上有改善，但是在解决具有一定非线性程度功能函数问题时出现计算效率和计算精度较低等问题.基于此，本文提出一种基于外罚函数法的结构可靠性分析方法，以解决一些非线性程度函数的约束优化问题，通过测试函数和工程算例结果表明该方法在实际应用中具有重大的意义.

1 外罚函数法理论及可靠度指标数学模型的建立

1.1 外罚函数法理论

罚函数法的构思是：根据约束条件本身的特点，将其转化为相应的惩罚函数加到目标函数中去，从而将约束优化问题转化为一系列的无约束优化问题来求解.

在一般的约束优化问题中，设结构的极小化目标函数为：

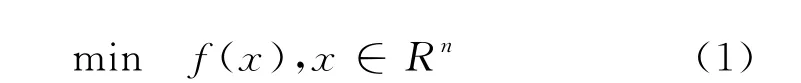
对应的约束条件为：

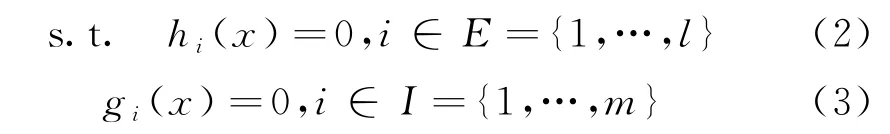
记可行域为：D={x∈Rn|hi=0(i∈E)，gi≥0(i∈I)}.构造罚函数：

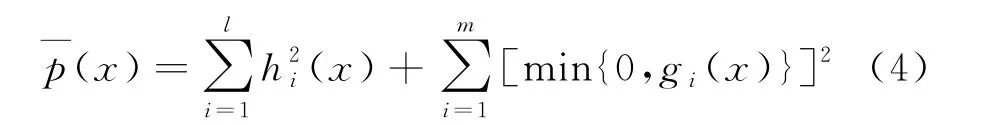
所得相应的增广目标函数：

在式(5)中M＞0为罚参数也叫做罚因子.在增广目标函数式中x的取值有以下两种情况：

1)当x∈D，也就是说当x是属于可行域里面时，P(x，M)=f(x)，这时目标函数并没有得到相应的惩罚；

2)当x∉D，即x不属于可行域里面时也就是在可行域内外面时，P(x，M)＞f(x)，此时目标函数受到了一定的惩罚.并且若M＞0其中M越大，则受到的惩罚也就越大，当M＞0足够大时，为了能够使增广目标函数P(x，M)达到极小，则对应的罚函数也必须要充分小才能够达到要求，即P(x，M)的极小点要充分逼近可行域D，使极小值点自然充分地逼近f(x)在D上的极小值.这样转化后使得求解一般约束优化问题转化为求解一系列无约束的优化问题minP(x，Mk)，当中的{Mk}为正数序列且Mk→+∞.

对于同时存在等式约束和不等式约束的问题 将上述两个罚函数组合成多元罚函数进行处理.

1.2 可靠度指标数学模型的建立

X1，X2，…，Xn是结构中n个任意分布的独立随机变量，由这些随机变量表示的结构极限状态方程为：

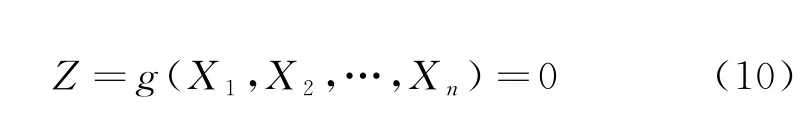
运用R-F(拉科维茨-菲斯莱法)将非正态变量当量正态化，得到等效正态的均值μ'xi，标准差σ'xi及可靠度指标β：

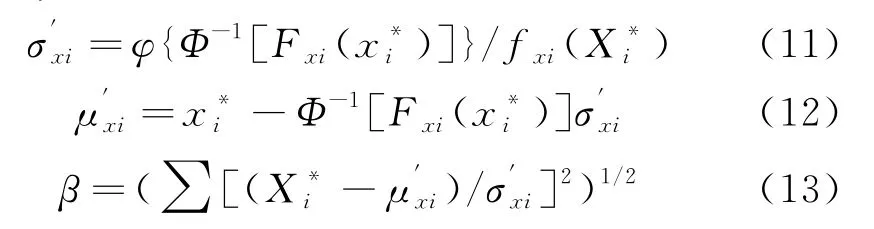
由于验算点未知，可以将β作为极限状态曲面上点P(X1，X2，…，Xn)的函数，通过相应的方法优化求解，得到β最小值，即可得到可靠度指标β和验算点P*.可靠度求解转化为如下约束优化模型：

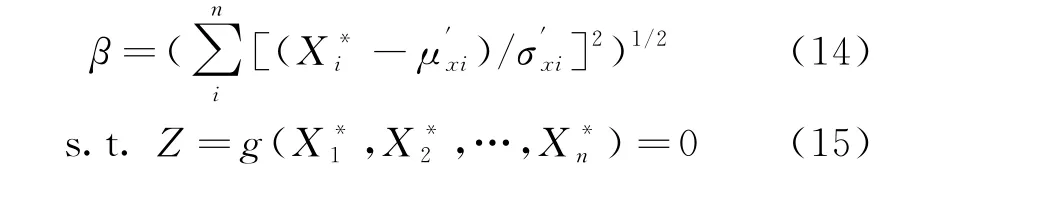
如果极限状态方程中的其中一个变量(Xj)可用其他变量表示为：

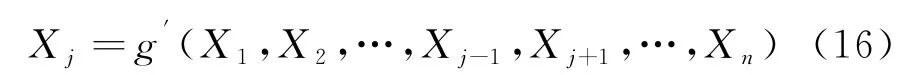
那么约束优化模型(15)可以表示为式(17)：

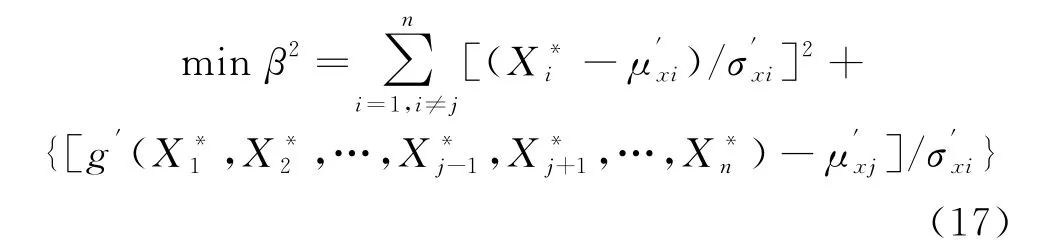
给定相应的功能方程及其变量的分布概型，根据1.1，1.2中所述的理论计算方法，同时结合式(6)，式(7)，式(14)和式(15)可求出可靠度β和x*.利用外罚函数法迭代可求得可靠度指标，具体的迭代步骤如下所示：

(1)选择适当的初始罚因子M0，初始点x0∈Rn，收敛精度0≤ε＜1和罚因子系数c＞1，令迭代步数k=1；

(2)构建相应的增广目标函数P(x，M)，求解极值点x*(M(k))；

(3)检验迭代终止条件：若|{f[X*(Mk)]-f[X*(M(k-1))]}/f[X*(Mk-1)]|≤ε，则停止迭代计算，输出最优解X*=X*(Mk)及可靠度β，否则转入第(4)步；

(4)取M(k-1)=cMk，x0=X*(Mk)，k=k+1，继续迭代.

2 可靠度算例

2.1 数值算例

极限状态方程：

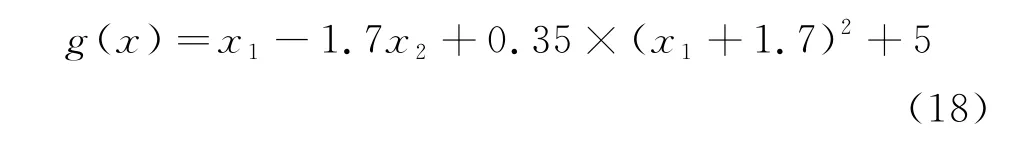
在式(18)中，x1与x2相互独立且均服从标准正态分布.根据外罚函数的理论，建立相应可靠指标计算数学模型，运用外罚函数法求解，经过6次迭代后，求得可靠指标β=2.5529，详细迭代计算结果见表1，对应的可靠指标和失效概率计算结果见表2.

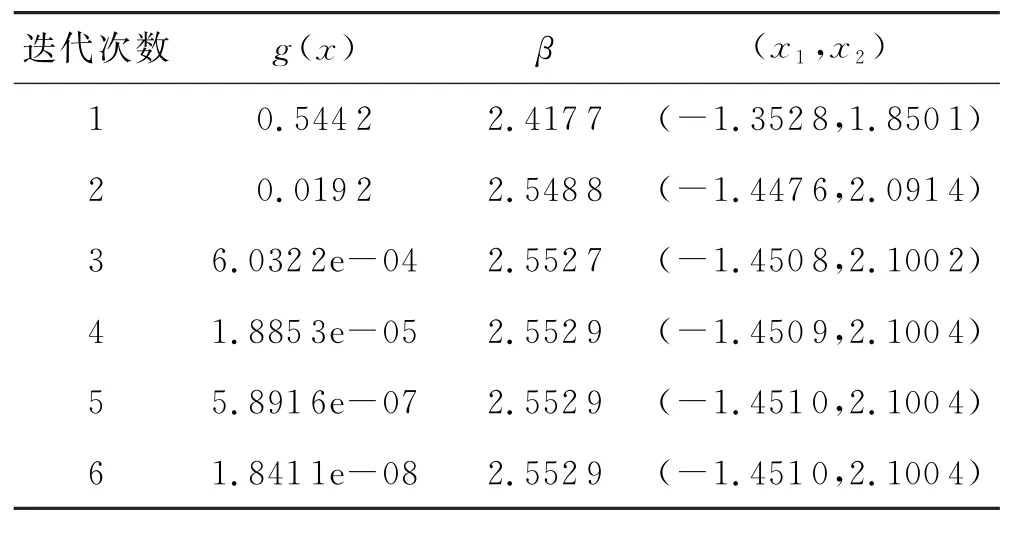
表1 外罚函数法迭代计算结果

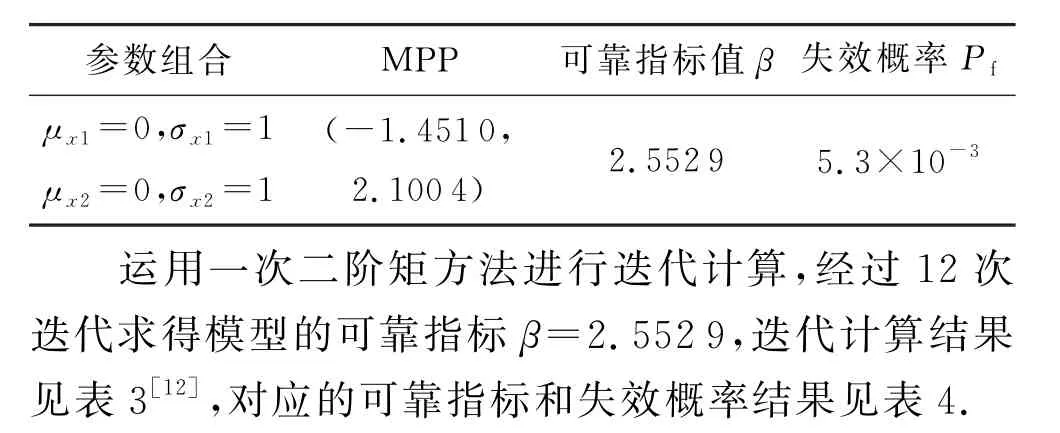
表2 外罚函数法可靠指标计算结果

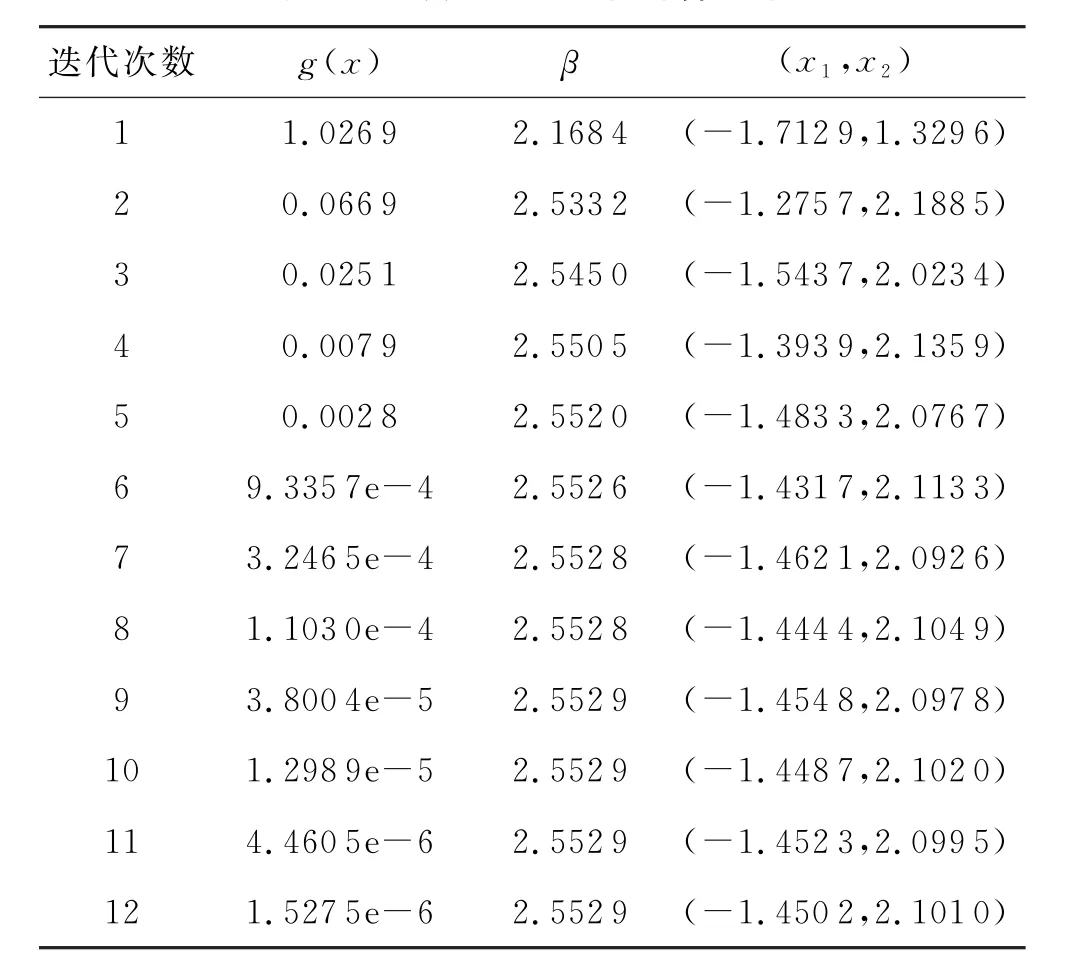
表3 一次二阶矩迭代计算结果

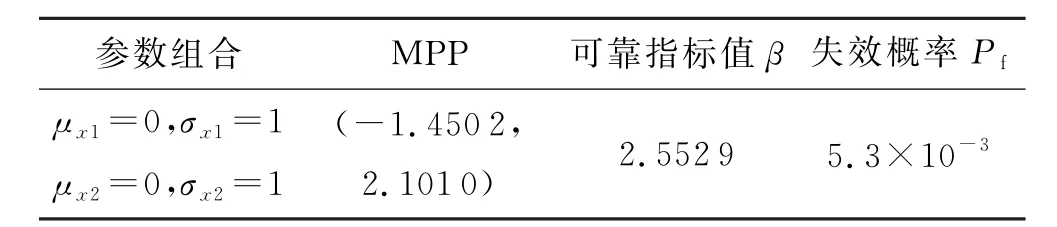
表4 一次二阶矩法可靠指标计算结果

根据表1和表3可以看出，运用外罚函数法求结构的可靠指标与一次二阶矩方法相比具有较高的计算效率，同时求得结构构件的失效概率Pf=5.3×10-3，表明该结构构件在规定时间和条件下能完成预定功能，并且具有很高的可靠性.

根据表1 可以看出随着迭代的进行，功能函数g(x)的值越来越小，最终收敛于零，功能函数值收敛于0表明满足收敛性要求.而可靠度指标也随着迭代步数的增加逐渐达到一个稳定的值.这表明运用外罚函数法迭代计算可靠度指标具有良好的收敛性并且计算结果精度较高.从图1看出，前两次的的迭代变化迅速，中间迭代变化缓慢，从图2看出最终迭代趋于一个稳定值.这表明运用外罚函数法在求解可靠性设计问题时具有较好的收敛性能.

2.2 车辆碰撞问题

汽车正面碰撞是交通事故中导致成员死亡的第一大主要因素，乘客受伤的主要原因是由于车身加速度及前端侵入量过大造成的.由于正面碰撞的缓冲区比较小，所以发生正面碰撞会使车体发生一定的变形.汽车在发生碰撞的过程中，影响乘员安全的主要因素有汽车结构的侵入量、侵入速度和侵入形态等.图3为某轿车正面碰撞有限元模型，汽车以时速为50 km/h撞上正前方刚性墙体，本例以B柱底部的峰值加速度a和最大侵入量作为碰撞安全性评估指标进行可靠性分析.对于正面碰撞安全设计，防撞梁、前轨和加强板是主要的能量吸收组件.

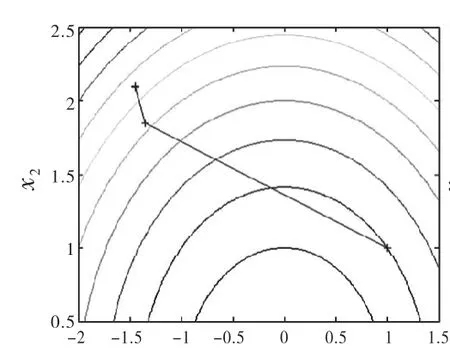
图1 目标函数等值线图

图3 某轿车的正面碰撞模型

如图3所示，选取防撞梁的厚度t1(对称)、前导轨的厚度t2(对称)、前轨盖厚度t3(对称)、加强板的厚度t4(对称)、处理弹性模量E和密度ρ作为设计变量.运用最优拉丁超立方设计方法[13]在设计空间选取40个样本点，并调用有限元法(FEM)[14]进行分析，创建其功能函数为：

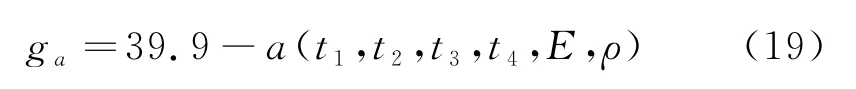
令式(19)中x1=t1，x2=t2，x3=t3，x4=t4，x5=E，x6=ρ，可以得到其极限状态方程.式中防撞梁的厚度t1、前导轨的厚度t2、前轨盖厚度t3、加强板的厚度t4、处理弹性模量E和密度ρ作为随机变量，来求解可靠度指标.具体的随机变量分布参数取值情况见表5.

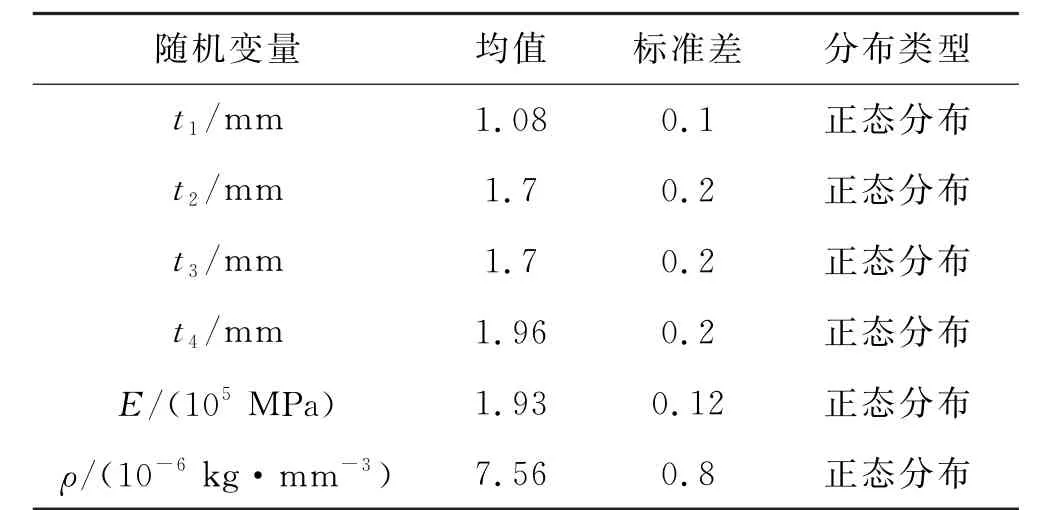
表5 各随机变量分布参数取值情况

根据外罚函数理论，计算求得可靠指标β=6.6748，其中可靠指标、失效概率计算数据及性能函数等计算结果见表6，可靠度指标值随迭代步数变化的曲线如图4所示.运用一次二阶矩方法迭代计算求得可靠指标β=6.5927，相应计算结果见表7，可靠指标随迭代步数变化曲线如图5所示.

表6 可靠指标及性能函数计算结果

图4 迭代步数与可靠度指标值所示图

表7 一次二阶矩法可靠指标及性能函数计算结果

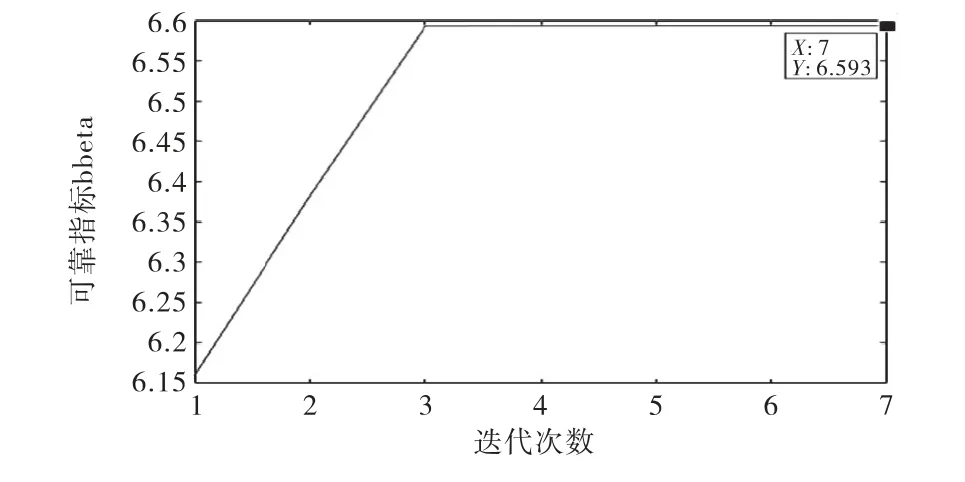
图5 迭代步数与可靠度指标值所示图

从图4可以看出，运用外罚函数法迭代计算经过5次迭代即可求得可靠指标，而根据图5可知运用一次二阶矩方法迭代7次求得可靠指标.在图4中随着迭代步数的增加，可靠指标逐渐达到稳定值，表明外法罚函数法在计算可靠指标时具有良好的收敛性，运用外罚函数法迭代具有较高的计算效率.从表6和表7可以看出，失效概率非常小几乎趋近于零，表明某轿车正面碰撞模型在预定条件下具有较高的可靠性.

3 结 论

本文提出了一种基于外罚函数法的结构可靠度分析方法，该方法可用于解决具有一定非线性程度的结构功能方程的可靠性分析问题，同时该方法对不同形式的约束能够建立相应的可靠度模型进行可靠度分析.测试函数的结果表明，对于线性程度较高的极限状态函数，使用外罚函数法进行迭代计算有较好的收敛性，可以计算出比较精确的可靠性指标.工程案例的结果表明，该方法对于非线性程度较高的极限状态方程，也具有精确的计算精度，且有较好的收敛性.某轿车设计变量区间满足要求，使用外罚函数法得到的失效概率非常小几乎趋近于零，表明某轿车正面碰撞模型可靠.

此外，数值和工程算例表明，未来通过引入多种形式的约束条件，建立相应的可靠性模型，并采用本文方法进行结构可靠性分析，将在实际工程中对结构性能的提高和可靠性的保证具有一定的指导意义.